【算法】动画图解Dijkstra算法及其实现代码

Dijkstra算法是基于贪心思想的一种求最短路径的算法。
他的实现基于优先队列这种数据结构

该算法的动画演示
该算法的详细讲解

手动模拟示意图的结果

实现代码：

#include <iostream>
#include <vector>
using namespace std;
#include<stack>
const int INF = 1000000000;
 
/*Dijkstra算法解决的是单源最短路径问题，即给定图MGrap(V,E)和起点s(起点又称为源点),
求从起点s到达其它顶点的最短距离，并将最短距离存储在矩阵d中*/
void Dijkstra(int n, int s, vector<vector<int>> MGrap, vector<bool>& vis, vector<int>& d, vector<int>& pre)
{
       /*
       param
       n：           顶点个数
       s：           源点
       MGrap：           图的邻接矩阵
       vis：         标记顶点是否已被访问
       d：           存储源点s到达其它顶点的最短距离
       pre：         存储从起点s到达顶点v的最短路径上v的前一个顶点 （新添加）
       */
       fill(d.begin(), d.end(), INF);                         //初始化最短距离矩阵，全部为INF
 
       for (int i = 0; i < n; ++i)                            //新添加
              pre[i] = i;
 
       d[s] = 0;                                              //起点s到达自身的距离为0
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                     //找到d[u]最小的u
              int MIN = INF;                                  //记录最小的d[u]
              for (int j = 0; j < n; ++j)                     //开始寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           u = j;
                           MIN = d[j];
                     }
              }
              //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
              if (u == -1)
                     return;
              vis[u] = true;                                  //标记u已被访问
              for (int v = 0; v < n; ++v)
              {
                     //遍历所有顶点，如果v未被访问&&u能够到达v&&以u为中介点可以使d[v]更优
                     if (vis[v] == false && d[u] + MGrap[u][v] < d[v]) {
                           d[v] = d[u] + MGrap[u][v];             //更新d[v]
                           pre[v] = u;                        //记录v的前驱顶点为u（新添加）
                     }
              }
       }
}
 
//输出从起点s到顶点v的最短路径
void DFSPrint(int s, int v, vector<int> pre)
{
       if (v == s) {
              cout << s << " ";
              return;
       }
       DFSPrint(s, pre[v], pre);
       cout << v << " ";
}
 // 打印最短路径
void PrintShortPath(vector<vector<int>> G, int v0, vector<int> P, vector<int> D){
    int i, k;
    stack<int> path;
    cout<<"顶点v"<<v0<<"到其他顶点之间的最短路径如下: "<<endl;
    for(i = 0; i < G.size(); ++i){
        if(i == v0) continue;
        cout<<"v"<<v0<<"--"<<"v"<<i<<" weight: "<<D[i]<<"  Shortest path: ";
        path.push(i);
        int k = P[i];
        while(k != 0){
            path.push(k);
            k = P[k];
        }
        path.push(v0);
        while(!path.empty()){
            if(path.size() != 1)
                cout<<path.top()<<"->";
            else
                cout<<path.top()<<endl;
            path.pop();
        }
    }
}

int main()
{
       int n = 6;
       vector<vector<int>> MGrap = { {0,1,INF,4,4,INF},
                                 {INF,0,INF,2,INF,INF},
                                 {INF,INF,0,INF,INF,1},
                                 {INF,INF,2,0,3,INF},
                                 {INF,INF,INF,INF,0,3},
                                 {INF,INF,INF,INF,INF,0} };
       vector<bool> vis(n);
       vector<int> d(n);
       vector<int> pre(n);
 
       Dijkstra(n,0,MGrap,vis,d,pre);
       for (auto x : d)
              cout << x << " ";
       cout << endl;
       //输出从起点s到顶点v的最短路径
       DFSPrint(0, 5, pre);
       cout<<endl;
       PrintShortPath(MGrap,0,pre,d);
       return 0;
}

运行结果：

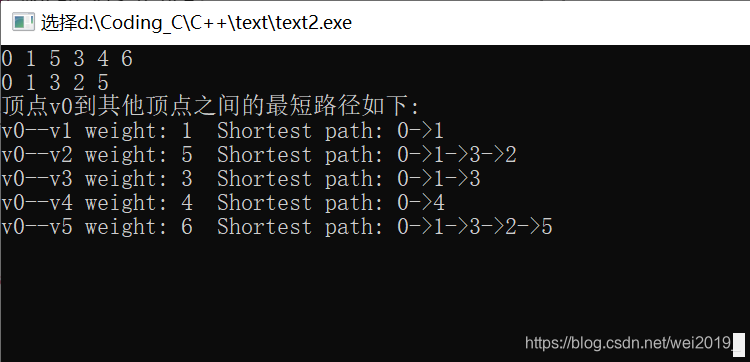
另外一种实现的方法

#include<iostream>
#include<stack>
using namespace std;

#define MAXVEX 9
#define INFINITY 65535

typedef int Patharc[MAXVEX];
typedef int ShortPathTable[MAXVEX];

typedef struct {
    int vex[MAXVEX];
    int arc[MAXVEX][MAXVEX];
    int numVertexes;
} MGraph;

// 构建图
void CreateMGraph(MGraph *G){
    int i, j, k;
    // 初始化图
    G->numVertexes = 9;
    for(i = 0; i < G->numVertexes; ++i){
        G->vex[i] = i;
    }
    for(i = 0; i < G->numVertexes; ++i){
        for(j = 0; j < G->numVertexes; ++j){
            if(i == j)
                G->arc[i][j] = 0;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITY;
        }
    }

    G->arc[0][1] = 1;
    G->arc[0][2] = 5;

    G->arc[1][2] = 3;
    G->arc[1][3] = 7;
    G->arc[1][4] = 5;

    G->arc[2][4] = 1;
    G->arc[2][5] = 7;

    G->arc[3][4] = 2;
    G->arc[3][6] = 3;

    G->arc[4][5] = 3;
    G->arc[4][6] = 6;
    G->arc[4][7] = 9;

    G->arc[5][7] = 5;

    G->arc[6][7] = 2;
    G->arc[6][8] = 7;

    G->arc[7][8] = 4;

    // 设置对称位置元素值
    for(i = 0; i < G->numVertexes; ++i){
        for(j = i; j < G->numVertexes; ++j){
            G->arc[j][i] = G->arc[i][j];
        }
    }
}

void ShortPath_Dijkstra(MGraph G, int v0, Patharc P, ShortPathTable D){
    int final[MAXVEX];
    int i;
    for(i = 0; i < G.numVertexes; ++i){
        final[i] = 0;
        D[i] = G.arc[v0][i];
        P[i] = 0;
    }
    D[v0] = 0;
    final[v0] = 1;
    for(i = 0; i < G.numVertexes; ++i){
        int min = INFINITY;
        int j, k, w;

        for(j = 0; j < G.numVertexes; ++j){// 查找距离V0最近的顶点
            if(!final[j] && D[j] < min){
                k = j;
                min = D[j];
            }
        }
        final[k] = 1;
        for(w = 0; w < G.numVertexes; ++w){// 更新各个顶点的距离
            if(!final[w] && (min + G.arc[k][w]) < D[w]){
                D[w] = min + G.arc[k][w];
                P[w] = k;
            }
        }
    }
}

// 打印最短路径
void PrintShortPath(MGraph G, int v0, Patharc P, ShortPathTable D){
    int i, k;
    stack<int> path;
    cout<<"顶点v"<<v0<<"到其他顶点之间的最短路径如下: "<<endl;
    for(i = 0; i < G.numVertexes; ++i){
        if(i == v0) continue;
        cout<<"v"<<v0<<"--"<<"v"<<i<<" weight: "<<D[i]<<"  Shortest path: ";
        path.push(i);
        int k = P[i];
        while(k != 0){
            path.push(k);
            k = P[k];
        }
        path.push(v0);
        while(!path.empty()){
            if(path.size() != 1)
                cout<<path.top()<<"->";
            else
                cout<<path.top()<<endl;
            path.pop();
        }
    }
}

int main(int argc, char const *argv[]) {
    int v0 = 0; // 源点
    MGraph G;
    Patharc P;
    ShortPathTable D;
    CreateMGraph(&G);
    ShortPath_Dijkstra(G, v0, P, D);
    PrintShortPath(G, v0, P, D);
    return 0;
}

如果题目给出的是无向边（即双向边）而不是有向边，又该如何解决呢？其实很简单，只需要把无向边当成两条指向相反的有向边即可。对邻接矩阵来说，一条u与v之间的无向边在输入时可以分别对G[u][v]和G[v][u]赋以相同的边权；而对于邻接表来说，只需要在u的邻接表Adj[u]末尾添加上v，并在v的邻接表Adj[v]末尾添加上u即可。