转自维基百科
计算复数 z 的 exp(z)
非常直接的给出公式
注意给三角函数的参数 y 是实数。
[编辑]计算复数 a 和 b 的 ab
直接给出公式:
如果 a = x + yi 且 b = u + vi,先把 a 转换到极坐标,需要找到满足如下条件的  和
和  :
:
或
-
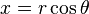 且
且
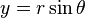
所以,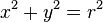 或
或  而且
而且  或
或  。
。
现在我们有:
所以:
指数因此是两个复数值的简单乘积生成复数结果,它可以接着通过如下公式转换回到正规的笛卡尔坐标:
这里的 p 是乘法的实部:
而 q 是乘法的虚部:
注意在这些计算中所有 
 ,
,  和
和  都是实数值。
都是实数值。 的结果因此是
的结果因此是  。
。
还要注意因为我们计算和使用了  而不是 r 自身,你不需要计算平方根。转而简单的计算
而不是 r 自身,你不需要计算平方根。转而简单的计算 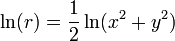 。预防潜在的上溢出并尽可能在计算
。预防潜在的上溢出并尽可能在计算 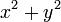 之前通过适当的 2 幂按比例缩减 x 和 y,如果
之前通过适当的 2 幂按比例缩减 x 和 y,如果  和
和  太大就会上溢出。如果你有下溢出的危险,在计算平方和之前通过适当的 2 的幂按比例增加它们。在任何一个情况下,你可以接着得到按比例缩放版本的
太大就会上溢出。如果你有下溢出的危险,在计算平方和之前通过适当的 2 的幂按比例增加它们。在任何一个情况下,你可以接着得到按比例缩放版本的  称为
称为 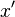 ,和按比例缩放版本的
,和按比例缩放版本的  称为
称为  ,因此得到:
,因此得到:
-
 和
和
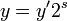
这里的  是缩放因子。
是缩放因子。
接着得到  这里的
这里的 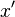 和
和  被缩放了使得平方和不上溢出或下溢出。如果
被缩放了使得平方和不上溢出或下溢出。如果  是非常大而
是非常大而  是非常小,因而不能找到这样一个缩放因子,你就会上溢出所以这个和本质上等于
是非常小,因而不能找到这样一个缩放因子,你就会上溢出所以这个和本质上等于  ,因为 y 被忽略了,因此你在这种情况下得到了
,因为 y 被忽略了,因此你在这种情况下得到了  和
和  。同样情况出现在
。同样情况出现在  非常小而
非常小而  非常大的时候。如果两个都非常小或都非常大就可以找到前面提到的缩放因子。
非常大的时候。如果两个都非常小或都非常大就可以找到前面提到的缩放因子。












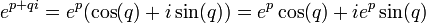

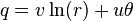
















 2958
2958

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








