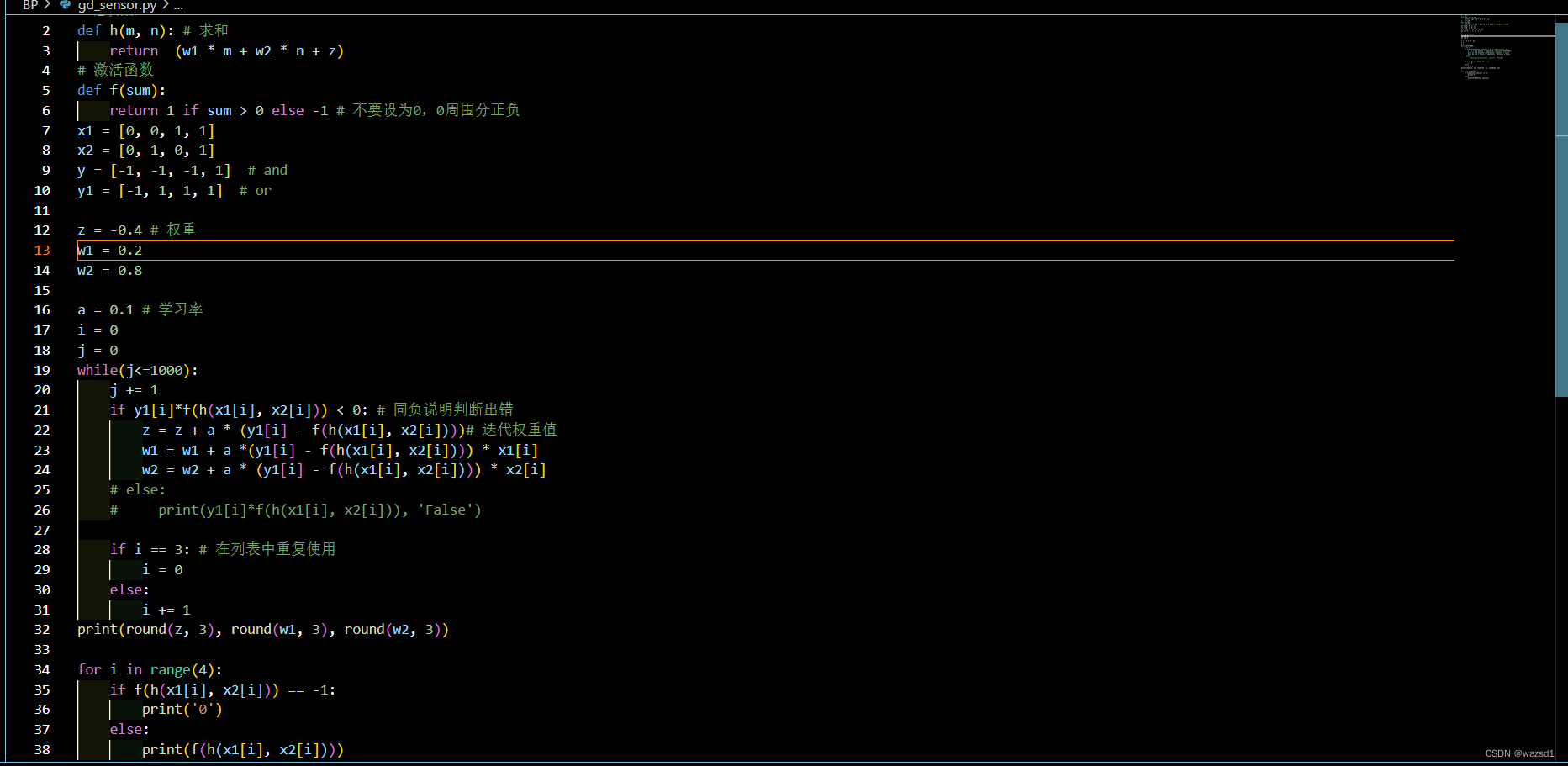
代码如下:
def h(m, n): # 求和
return (w1 * m + w2 * n + z)
# 激活函数,改变它,可以训练出自适应的权重和偏置
def f(sum):
return 1 if sum > 0 else -1 # 不要设为0,0周围分正负
x1 = [0, 0, 1, 1]
x2 = [0, 1, 0, 1]
y = [-1, -1, -1, 1] # and
y1 = [-1, 1, 1, 1] # or
z = -0.4 # 权重
w1 = 0.2
w2 = 0.8
a = 0.1 # 学习率
i = 0
j = 0
while(j<=1000):
j += 1
if y1[i]*f(h(x1[i], x2[i])) < 0: # 同负说明判断出错
z = z + a * (y1[i] - f(h(x1[i], x2[i])))# 迭代权重值
w1 = w1 + a *(y1[i] - f(h(x1[i], x2[i]))) * x1[i]
w2 = w2 + a * (y1[i] - f(h(x1[i], x2[i]))) * x2[i]
# else:
# print(y1[i]*f(h(x1[i], x2[i])), 'False')
if i == 3: # 在列表中重复使用
i = 0
else:
i += 1
print(round(z, 3), round(w1, 3), round(w2, 3))
for i in range(4):
if f(h(x1[i], x2[i])) == -1:
print('0')
else:
print(f(h(x1[i], x2[i])))
改变激活函数的分界点,查看权重和偏置是否可以自适应:
return 1 if sum > 0 else -1 -----> return 1 if sum >10 else -1 ------> return 1 if sum > 15 else -1
结果分别如下:



因此,可以下结论在激活函数改变的情况下,权重和偏置可以自适应。
实现与或逻辑关系:只要修改引入的真实值y即可,y1代表着或,y代表着与。
and关系实现:

or关系实现: 





















 1639
1639

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








