梯度下降训练线性回归方程

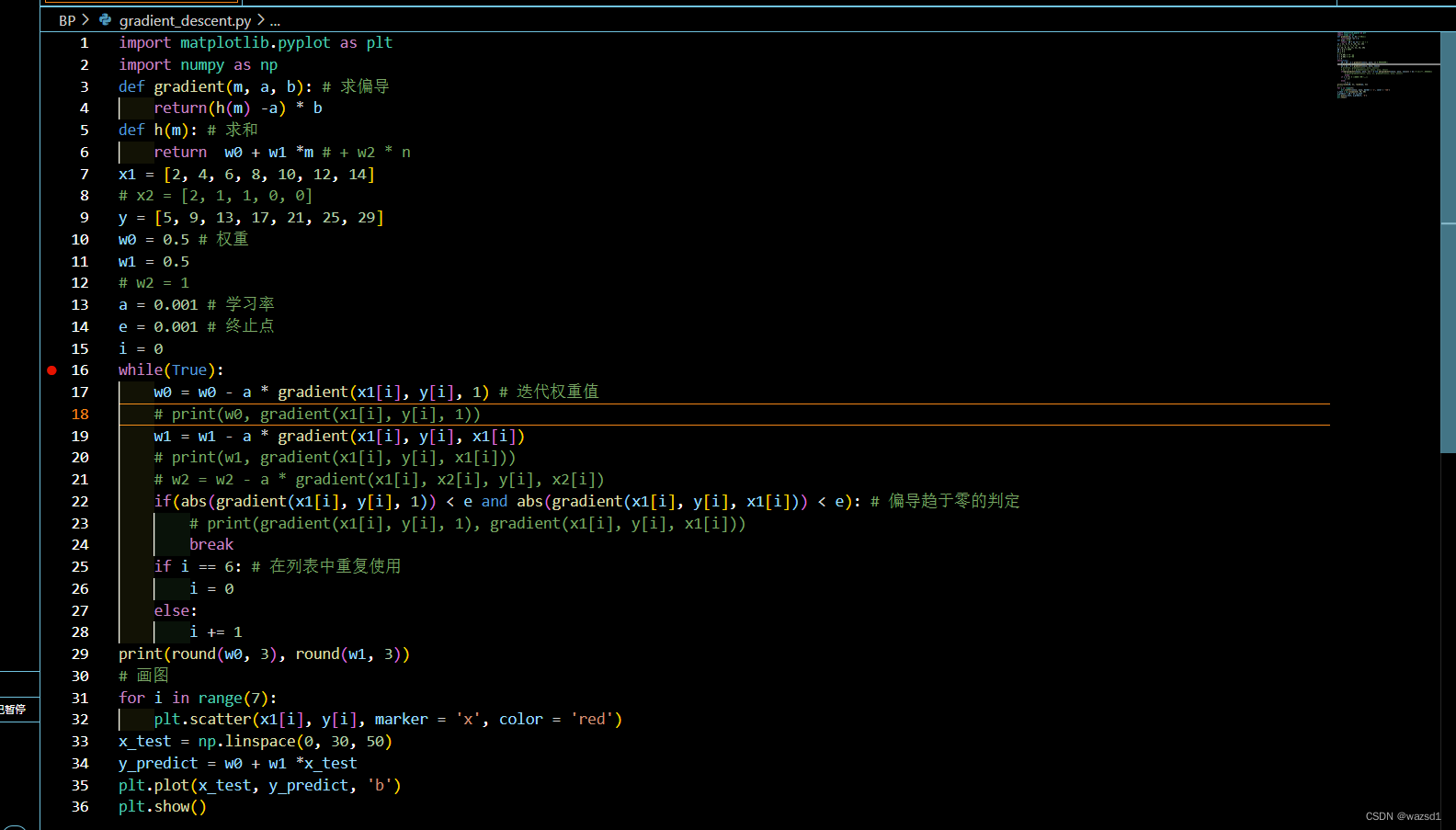
 代码如下：

import matplotlib.pyplot as plt

import numpy as np

def gradient(m, a, b): # 求偏导

    return(h(m) -a) * b

def h(m): # 求和

    return  w0 + w1 *m # + w2 * n

x1 = [2, 4, 6, 8, 10, 12, 14]

# x2 = [2, 1, 1, 0, 0]

y = [5, 9, 13, 17, 21, 25, 29]

w0 = 0.5 # 权重

w1 = 0.5

# w2 = 1

a = 0.001 # 学习率

e = 0.001 # 终止点

i = 0

while(True):

    w0 = w0 - a * gradient(x1[i], y[i], 1) # 迭代权重值

    # print(w0, gradient(x1[i], y[i], 1))

    w1 = w1 - a * gradient(x1[i], y[i], x1[i])

    # print(w1, gradient(x1[i], y[i], x1[i]))

    # w2 = w2 - a * gradient(x1[i], x2[i], y[i], x2[i])

    if(abs(gradient(x1[i], y[i], 1)) < e and abs(gradient(x1[i], y[i], x1[i])) < e): # 偏导趋于零的判定

        # print(gradient(x1[i], y[i], 1), gradient(x1[i], y[i], x1[i]))

        break

    if i == 6: # 在列表中重复使用

        i = 0

    else:

        i += 1

print(round(w0, 3), round(w1, 3))

# 画图

for i in range(7):

    plt.scatter(x1[i], y[i], marker = 'x', color = 'red')

x_test = np.linspace(0, 30, 50)

y_predict = w0 + w1 *x_test

plt.plot(x_test, y_predict, 'b')

plt.show()

设计的一元线性回归函数是：y = 2x + 1

最终权重应接近于：w0 = 1, w1 = 2

 

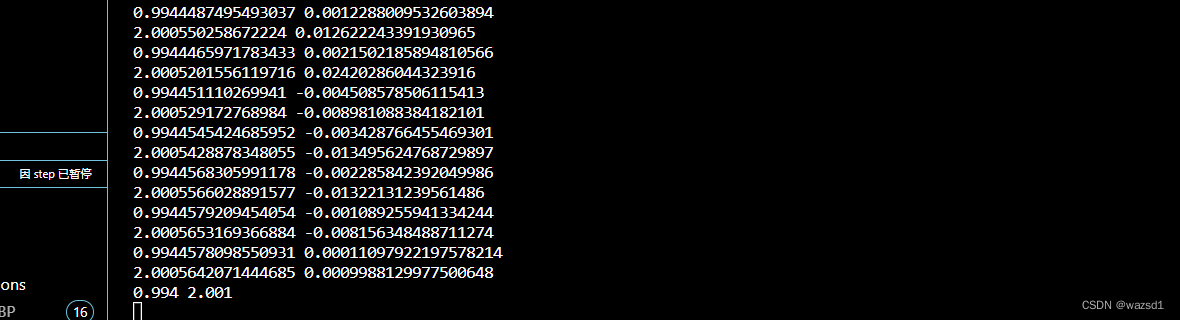
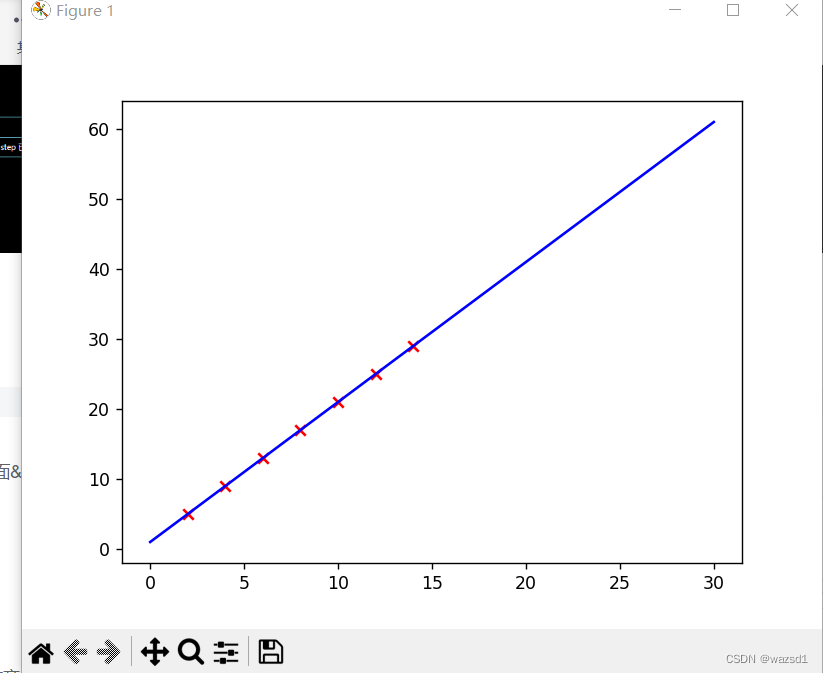
 以上可以看出，权值最终收敛。