线性单元模板和SGD以及学习率的一些介绍

线性单元和感知器的区别在于激活函数的不同：

 线性单元：

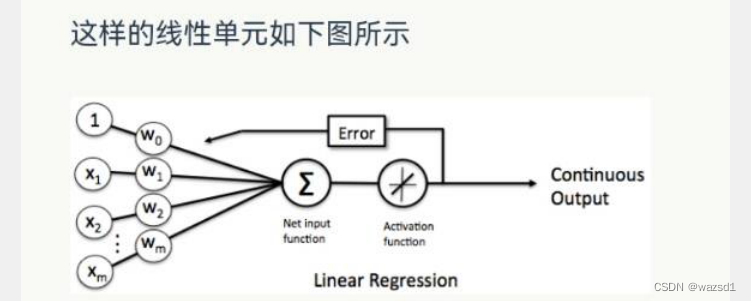
 感知器：

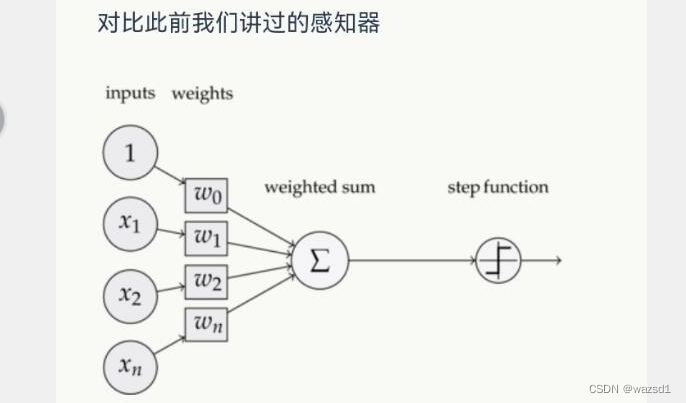
 BGD：每次更新的迭代，要遍历训练数据中所有的样本进行计算，我们称这种算法叫做批梯度下降(Batch Gradient Descent)。

SGD：每次更新的迭代，只计算一个样本。这样对于一个具有数百万样本的训练数据，完成一次遍历就会对更新数百万次，我们称为随机梯度下降算法(Stochastic Gradient Descent, SGD)。

随机梯度下降所带来的波动有个好处就是，对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。

import matplotlib.pyplot as plt
import numpy as np
# 线性单元
def h(m): # 求和
    return  (w1 * m + z)
# 激活函数, y=x简单线性， 可以将想拟合的函数写入，比如一些非凸函数
# 对非凸函数，初始值的不同，可导致最终训练到不同的鞍点和局部最小值
def f(x):
    return x
x1 = [3, 5, 7, 8, 10]
y = [33, 49, 72, 79, 101]

z = -0.4 # 权重
w1 = 0.2

a = 0.00001 # 学习率,太高会无法拟合，跳出或循环在一个范围内
e = 0.00001
i = 0
j = 0
while True:
    if abs(y[i] - f(h(x1[i]))) < e and abs((y[i] - f(h(x1[i]))) * x1[i]) < e: # 偏导同时趋于零
        break
    else:
        z = z + a * (y[i] - f(h(x1[i])))# 迭代权重值
        w1 = w1 + a *(y[i] - f(h(x1[i]))) * x1[i]
        print(x1[i], f(h(x1[i])))
    # j += 1
    # if j>=100000:
    #     break

    if i == 4: # 在列表中重复使用
        i = 0
    else:
        i += 1
print(round(z, 3), round(w1, 3))

# 画图
for i in range(5):
    plt.scatter(x1[i], y[i], marker = 'x', color = 'red')
x_test = np.linspace(0, 20)
y_predict = z + w1 *x_test
plt.plot(x_test, y_predict, 'b')
plt.show()

上述代码是令激活函数为y = x，这其实并未对线性回归方程造成多大的改变。其结果如下：

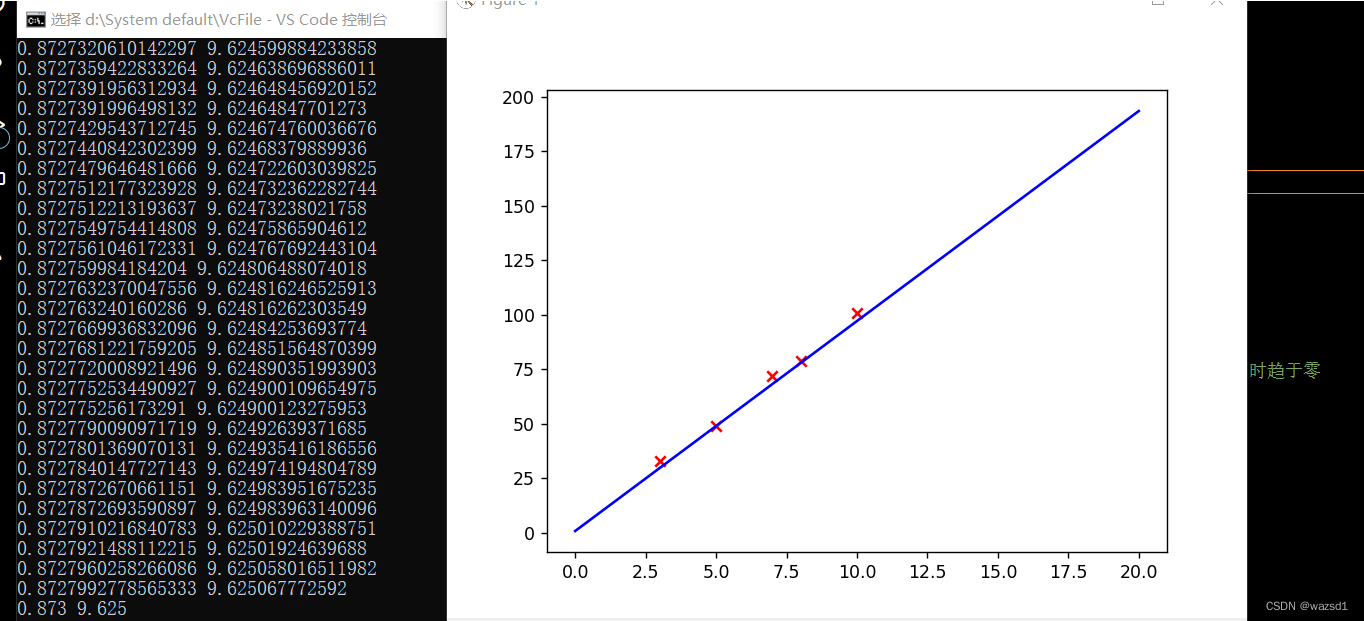
# 线性单元
def h(m): # 求和
    return  (w1 * m + z)
# 激活函数, y=x简单线性， 可以将想拟合的函数写入，比如一些非凸函数
# 对非凸函数，初始值的不同，可导致最终训练到不同的鞍点和局部最小值
def f(x):
    return x * x
x1 = [3, 5, 7, 8, 10]
y = [33, 49, 72, 79, 101]

z = -0.4 # 权重
w1 = 0.2

a = 0.00001 # 学习率,太高会无法拟合，跳出或循环在一个范围内
e = 0.00001
i = 0
j = 0
while True:
    if abs(y[i] - f(h(x1[i]))) < e and abs((y[i] - f(h(x1[i]))) * x1[i]) < e: # 偏导同时趋于零
        break
    else:
        z = z + a * (y[i] - f(h(x1[i])))# 迭代权重值
        w1 = w1 + a *(y[i] - f(h(x1[i]))) * x1[i]
        print(x1[i], f(h(x1[i])))
    # j += 1
    # if j>=100000:
    #     break

    if i == 4: # 在列表中重复使用
        i = 0
    else:
        i += 1
print(round(z, 3), round(w1, 3))

这是令激活函数为y = x**2函数，结果如下：

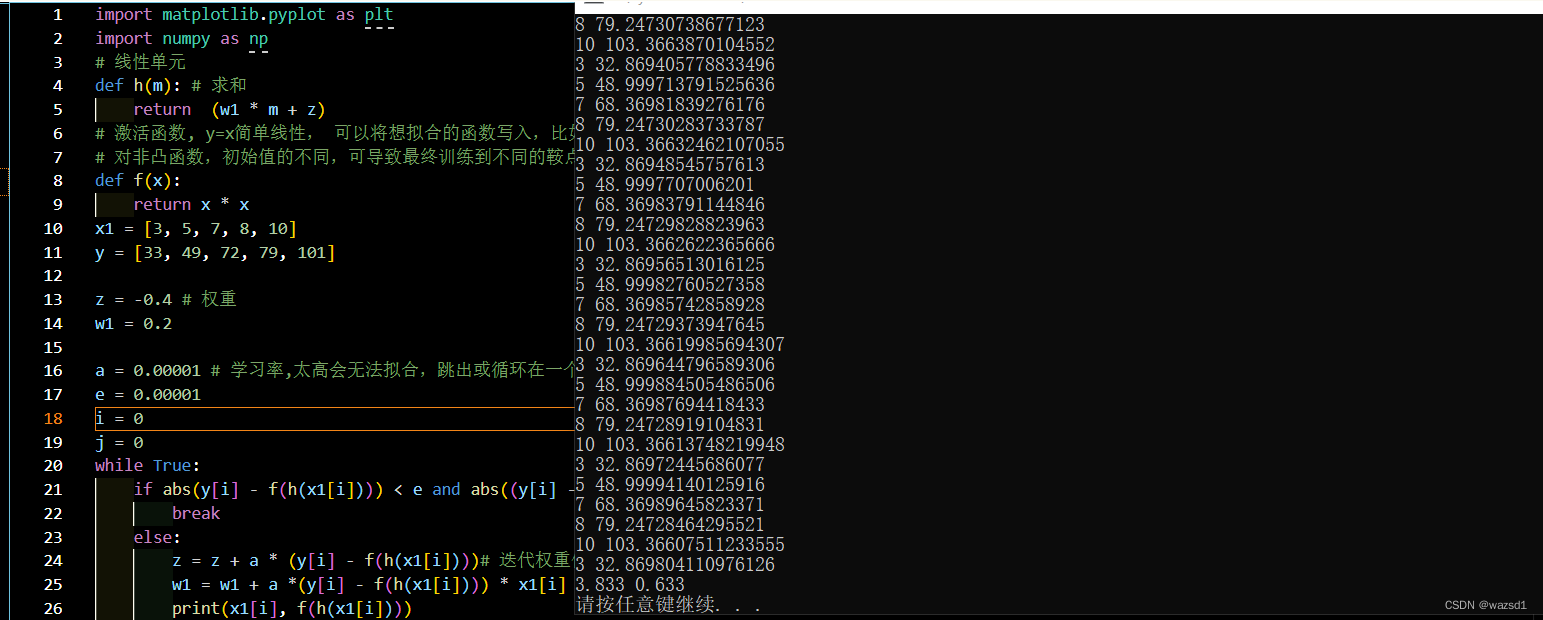
可以看到不同x的预测值，与实际值相差不大，好的学习率和e可以让拟合的效果更好。

对于学习率和初始点对非凸函数的影响，学习率不宜太大或太小。太小会导致你的程序运行的时间和次数过多，太大可能会造成越过最小点并导致数据在一个区间内循环无法拟合。初始点不同可能会造成最终训练到局部最小值或鞍点。如上述的代码，当我设置学习率为0.01时，太大而造成数据无法拟合：

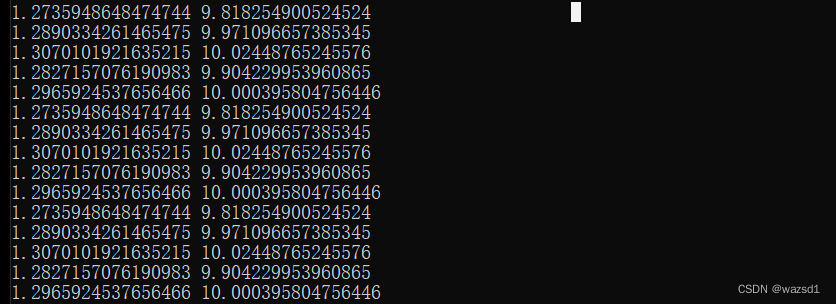
 学习率还有一个问题是：固定的步长在后期会随着临近最低点而相对的变大，就是说学习率固定对前面来说或许很小，但对后面的一段时间来说是很长的，所以我们想使用逐渐趋于0的学习率。然而，逐渐趋于0的学习率又带来了大后期收敛的越来越慢的问题，这就又引出了SVRG算法，这里就不讨论了。 

学习率的调整方法：

1、从自己和其他人一般的经验来看，学习率可以设置为3、1、0.5、0.1、0.05、0.01、0.005，0.005、0.0001、0.00001具体需结合实际情况对比判断，小的学习率收敛慢，但能将loss值降到更低。

2、根据数据集的大小来选择合适的学习率，当使用平方和误差作为成本函数时，随着数据量的增多，学习率应该被设置为相应更小的值（从梯度下降算法的原理可以分析得出）。另一种方法就是，选择不受数据集大小影响的成本函数-均值平方差函数。

3、训练全过程并不是使用一个固定值的学习速度，而是随着时间的推移让学习率动态变化，比如刚开始训练，离下山地点的最优值还很远，那么可以使用较大的学习率下的快一点，当快接近最优值时为避免跨过最优值，下山速度要放缓，即应使用较小学习率训练，具体情况下因为我们也不知道训练时的最优值，所以具体的解决办法是：在每次迭代后，使用估计的模型的参数来查看误差函数的值，如果相对于上一次迭代，错误率减少了，就可以增大学习率如果相对于上一次迭代，错误率增大了，那么应该重新设置上一轮迭代的值，并且减少学习率到之前的50%。因此，这是一种学习率自适应调节的方法。在Caffe、Tensorflow等深度学习框架中都有很简单直接的学习率动态变化设置方法。

学习率缓减机制：

 要注意的是，exponential_decay适用于tensflow1.X版本的2.版本，在下载后tensorflow后发现没有exponential_decay时差点晕了，因为版本基本都是2.x的。

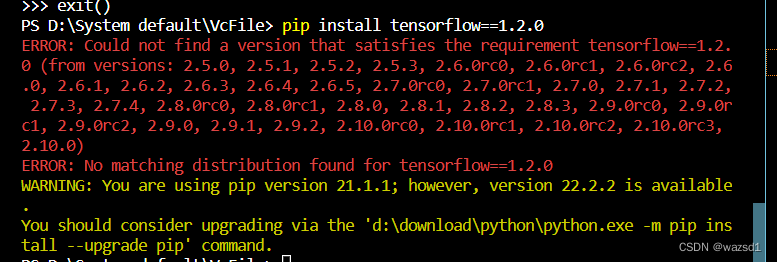
 因此，就手写了指数衰减法：

import matplotlib.pyplot as plt
import numpy as np
# 线性单元
def h(m): # 求和
    return  (w1 * m + z)
# 激活函数, y=x简单线性， 可以将想拟合的函数写入，比如一些非凸函数
# 对非凸函数，初始值的不同，可导致最终训练到不同的鞍点和局部最小值
def f(x):
    return x
x1 = [3, 5, 7, 8, 10]
y = [33, 48, 72, 80, 97]

z = 0.5 # 权重
w1 = 9.78

a0 = 0.01 # 学习率,太高会无法拟合，跳出或循环在一个范围内
a = 0.01
e = 0.01
i = 0
global_steps = 0
decay_steps = 50000
decay_rate = 0.1
while True:

    global_steps += 1
    if global_steps >= 500000:
        break

    # 指数衰减法
    if a >= 0.000001:  # 要保证学习率不要太小，否则太慢
        a =a0 * (decay_rate ** int((global_steps/decay_steps)))

    # exponential_decay适用于tensflow1.X版本的2.版本
    # global_step = tf.Variable(0)
    # a = tf.train.exponential_decay(
    #     a0,
    #     global_step,
    #     decay_steps=1000,
    #     decay_rate=0.1,
    #     staircase=True)

    if abs(y[i] - f(h(x1[i]))) < e and abs((y[i] - f(h(x1[i]))) * x1[i]) < e: # 偏导同时趋于零
        break
    else:
        z = z + a * (y[i] - f(h(x1[i])))# 迭代权重值
        w1 = w1 + a *(y[i] - f(h(x1[i]))) * x1[i]
        print(z, w1)
    
    if i == 4: # 在列表中重复使用
        i = 0
    else:
        i += 1
print(round(z, 3), round(w1, 3))

# 画图
for i in range(5):
    plt.scatter(x1[i], y[i], marker = 'x', color = 'red')
x_test = np.linspace(0, 20)
y_predict = z + w1 *x_test
plt.plot(x_test, y_predict, 'b')
plt.show()

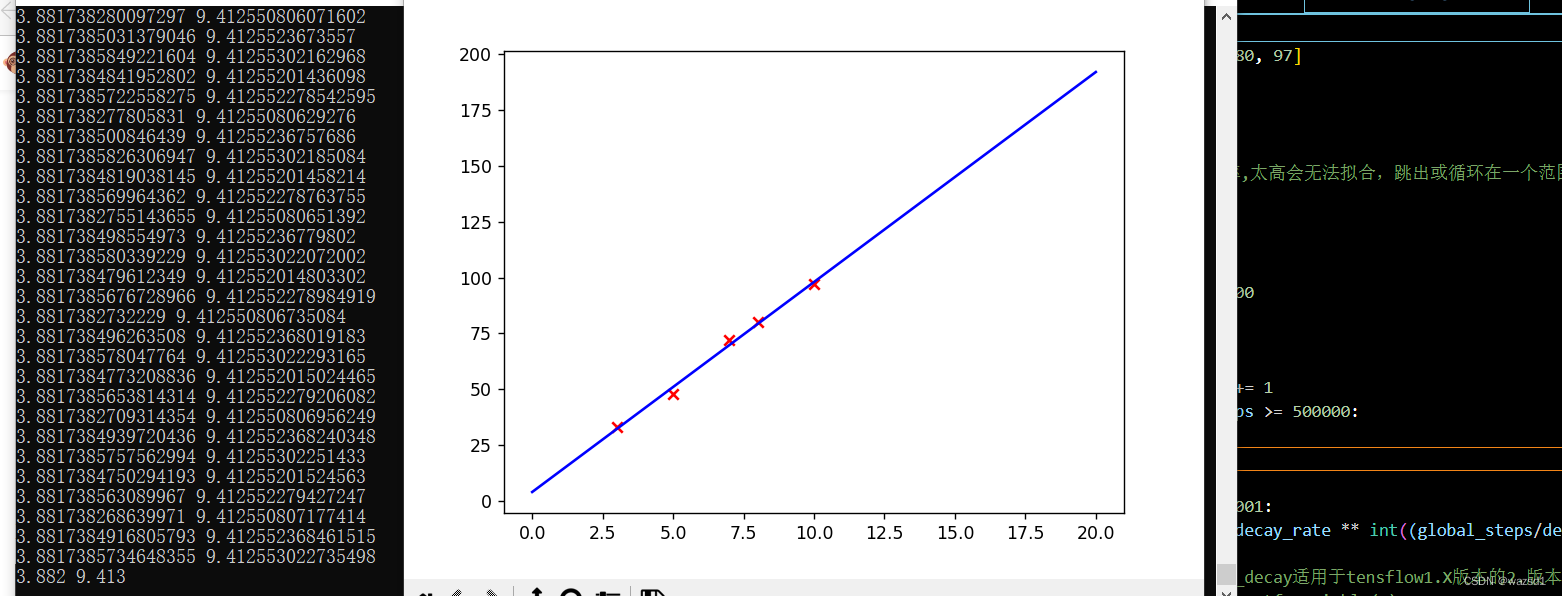
前面说过逐渐趋于0的学习率又带来了大后期收敛的越来越慢的问题，解决方法是SVRG算法。如果没有设置迭代次数的限制，运行时间真的非常长。

 参考：(20条消息) 深度学习笔记(五)：学习率过大过小对于网络训练有何影响以及如何解决_ZZY_dl的博客-优快云博客_学习率过大