LeetCode.1143 最长公共子序列

最新推荐文章于 2022-07-31 12:18:14 发布

难过的风景

最新推荐文章于 2022-07-31 12:18:14 发布

阅读量93

点赞数

CC 4.0 BY-SA版权

分类专栏：力扣题解文章标签： leetcode 动态规划

本文链接：https://blog.youkuaiyun.com/wazk2008/article/details/115419543

力扣题解专栏收录该内容

82 篇文章

订阅专栏

本文解析了如何使用动态规划解决LeetCode上的最长公共子序列问题，介绍了单数组和双数组动态规划的思路，并提供了Java代码实例。通过对比和官方题解，展示了如何构建两维dp数组来找到两个字符串的最长公共子序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

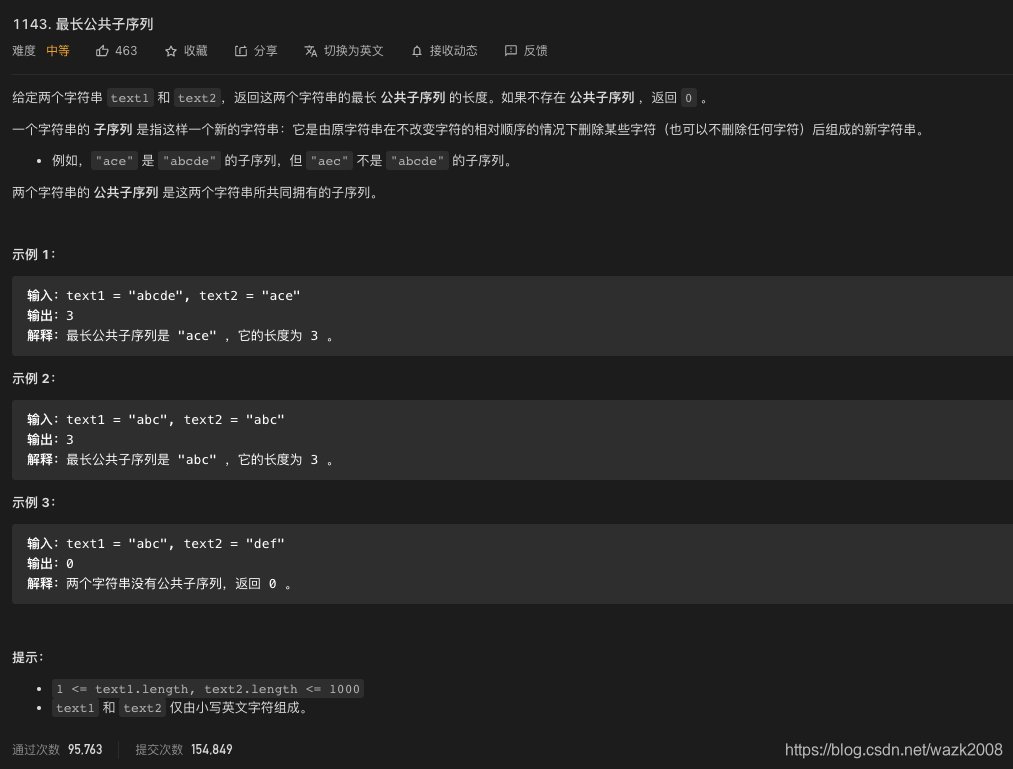
原题

https://leetcode-cn.com/problems/longest-common-subsequence/

在这里插入图片描述

思路

动态规划也是有套路的：
- 单个数组或者字符串要用动态规划时，可以把动态规划 dp[i] 定义为 nums[0:i] 中想要求的结果；
- 当两个数组或者字符串要用动态规划时，可以把动态规划定义成两维的 dp[i][j]，其含义是在 A[0:i] 与 B[0:j]之间匹配得到的想要的结果。

https://leetcode-cn.com/problems/longest-common-subsequence/solution/zui-chang-gong-gong-zi-xu-lie-by-leetcod-y7u0/
https://leetcode-cn.com/problems/longest-common-subsequence/solution/fu-xue-ming-zhu-er-wei-dong-tai-gui-hua-r5ez6/

题解

package com.leetcode.code;

/**
 * @Description:
 * @ClassName: Code1143
 * @Author: ZK
 * @Date: 2021/4/3 18:29
 * @Version: 1.0
 */
public class Code1143 {

    public static void main(String[] args) {
        String text1 = "abcde";
        String text2 = "ace";
        System.out.println(longestCommonSubsequence(text1, text2));
    }

//    动态规划
    public static int longestCommonSubsequence(String text1, String text2) {
//        动态规划也是有套路的：
//        单个数组或者字符串要用动态规划时，可以把动态规划 dp[i] 定义为 nums[0:i] 中想要求的结果；
//        当两个数组或者字符串要用动态规划时，可以把动态规划定义成两维的 dp[i][j]，其含义是在 A[0:i] 与 B[0:j]之间匹配得到的想要的结果。

//        官方题解
//        https://leetcode-cn.com/problems/longest-common-subsequence/solution/zui-chang-gong-gong-zi-xu-lie-by-leetcod-y7u0/

        int m = text1.length();
        int n = text2.length();
        int[][] dp = new int[m+1][n+1];
        for (int i = 1; i <= m; i++) {
            char c1 = text1.charAt(i-1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.charAt(j-1);
                if (c1 == c2) {
                    dp[i][j] = dp[i-1][j-1]+1;
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        return dp[m][n];
    }

}