LeetCode.面试题 17.21. 直方图的水量_leetcode 直方图存水-优快云博客

本文链接：https://blog.youkuaiyun.com/wazk2008/article/details/115395795

该博客介绍了如何利用动态规划解决LeetCode上的接雨水问题（又称柱状图中最大的水池面积）。作者首先阐述了问题的核心思想，即计算每个位置能够存储的水量，并遵循短板原则。接着，通过两次遍历数组，分别获取每个元素左侧和右侧的最大高度，然后计算每个位置的储水量并累加，最终得到总储水量。整个过程的时间复杂度为O(n)。此外，博客还提供了完整的Java代码实现作为解题示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题

https://leetcode-cn.com/problems/volume-of-histogram-lcci/

在这里插入图片描述

思路

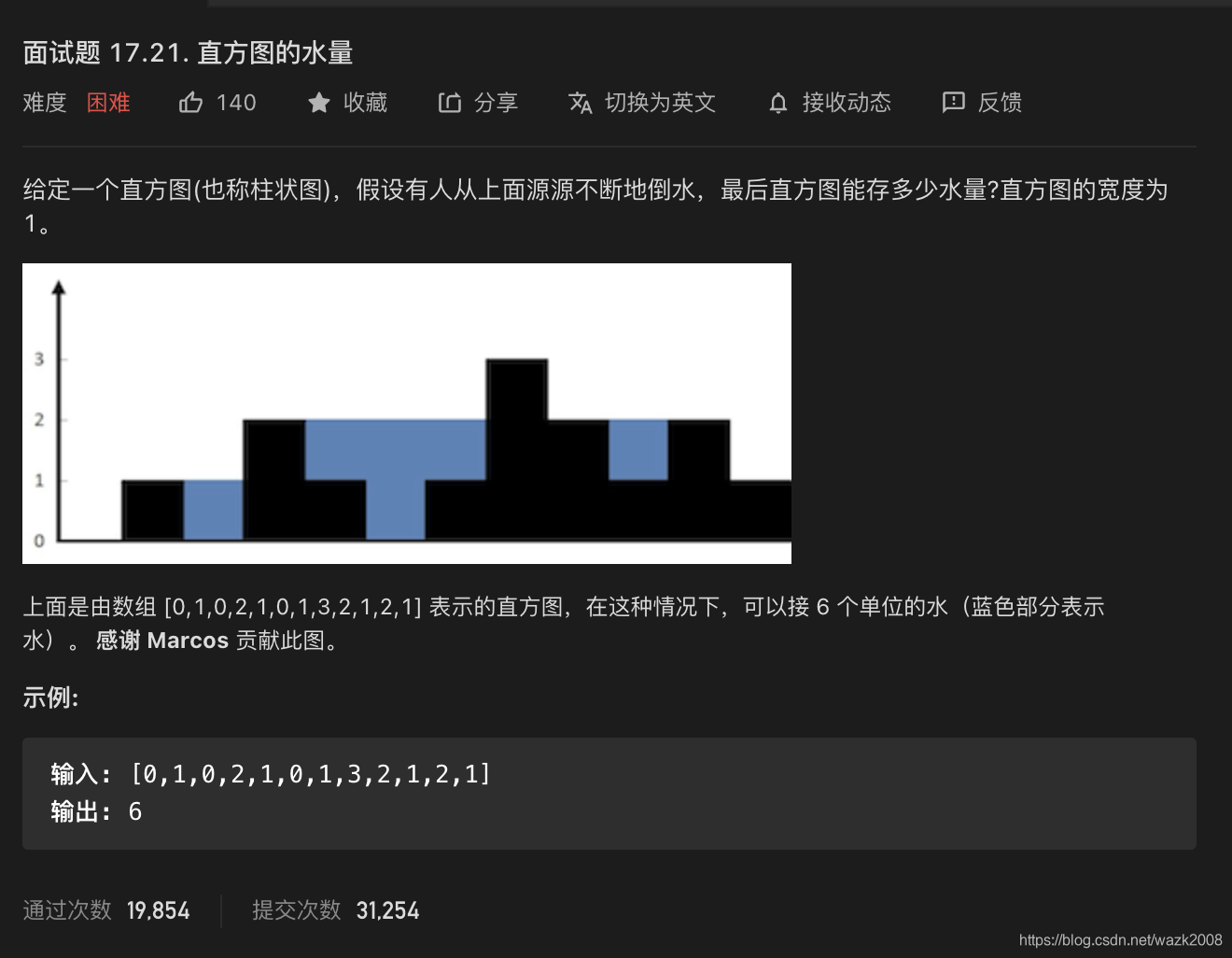
解题思路：只有凹的地方能存水，存水量遵循短板原则，所以用每个位置左右两侧最大值中的较小者减当前位置的值即可得到当前位置储水量。

解题方法：先倒叙遍历，用数组记录每个位置其右侧最大值max右，再正序遍历，时刻记录并更新当前位置左侧的最大值max左，然后当max左>当前值 && max右>当前值的时候，表示当前位置可以储水，计算当前位置储水量c=Min(max左，max右)-当前值（注：c>0一定成立），最后每个位置的c累加一起的和即为总储水量。

时间复杂度：O(n)

42. 接雨水同理，解法一样

题解

package cn.codemao.botmao.admin;

/**
 * @author: zhangkun@codemao.cn
 * @description:
 * @create: 2021-04-02 11:55
 * @Version 1.0
 **/
public class Code17$21 {

    public static void main(String[] args) {
        int[] height = {0,1,0,2,1,0,1,3,2,1,2,1};
        int res = trap(height);
        System.out.println(res);
    }

    public static int trap(int[] height) {
        int res = 0;
        int len = height.length;
        if (len == 0) {
            return 0;
        }
//        获取每个元素左边的最大值（不包括当前元素值）
        int[] leftMax = getLeftMax(height);
//        获取每个元素右边的最大值（不包括当前元素值）
        int[] rightMax = getRightMax(height);

        for (int i = 0; i < len; i++) {
            int cur = height[i];
            int left = leftMax[i];
            int right = rightMax[i];
            if (left > cur && right > cur) {
                res += Math.min(left, right) - cur;
            }
        }

        return res;
    }
    
//    获取每个元素左边的最大值（不包括当前元素值）
    public static int[] getLeftMax(int[] arr){
        int len = arr.length;
        int[] res = new int[len];
        
//        第一个元素左边的最大值为0，其左边啥也没有
        res[0] = 0;
        for (int i = 1; i < len; i++) {
//            此处有点类似于动态规划，获取右边最大值同理
            res[i] = Math.max(res[i-1], arr[i-1]);
        }

        return res;
    }
    
//    获取每个元素右边的最大值（不包括当前元素值）
    public static int[] getRightMax(int[] arr){
        int len = arr.length;
        int[] res = new int[len];

        res[len-1] = 0;
        for (int i = len-2; i >= 0; i--) {
            res[i] = Math.max(res[i+1], arr[i+1]);
        }

        return res;
    }


}