【重温经典】滑动窗口最大值

【重温经典】滑动窗口最大值

基础

Deque有三种使用形式：

//普通队列(一端进另一端出):
Queue queue = new LinkedList()或Deque deque = new LinkedList()
//双端队列(两端都可进出)
Deque deque = new LinkedList()
//堆栈
Deque deque = new LinkedList()

• Deque是一个线性collection，支持在两端插入和移除元素。名称 deque 是“double ended queue（双端队列）”的缩写，通常读为“deck”。大多数 Deque 实现对于它们能够包含的元素数没有固定限制，但此接口既支持有容量限制的双端队列，也支持没有固定大小限制的双端队列。

• 此接口定义在双端队列两端访问元素的方法。提供插入、移除和检查元素的方法。每种方法都存在两种形式：一种形式在操作失败时抛出异常，另一种形式返回一个特殊值（null 或 false，具体取决于操作）。插入操作的后一种形式是专为使用有容量限制的 Deque 实现设计的；在大多数实现中，插入操作不能失败。
  下面是12种方法：

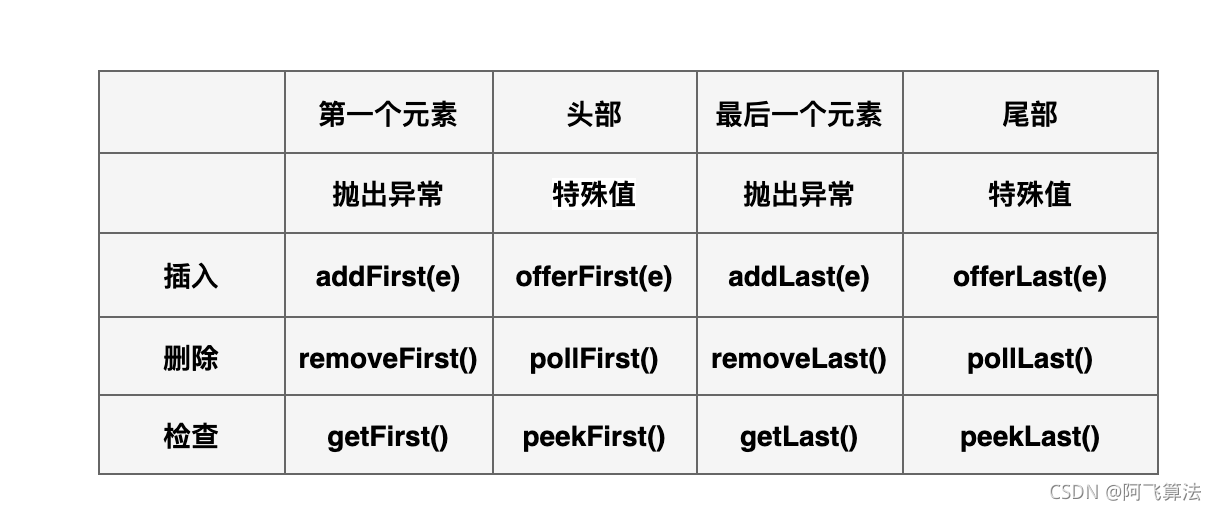
• Deque接口扩展(继承)了 Queue 接口。在将双端队列用作队列时，将得到 FIFO（先进先出）行为。将元素添加到双端队列的末尾，从双端队列的开头移除元素。从 Queue 接口继承的方法完全等效于 Deque 方法

• 双端队列也可用作 LIFO（后进先出）堆栈。应优先使用此接口而不是遗留 Stack 类。在将双端队列用作堆栈时，元素被推入双端队列的开头并从双端队列开头弹出。堆栈方法完全等效于 Deque 方法

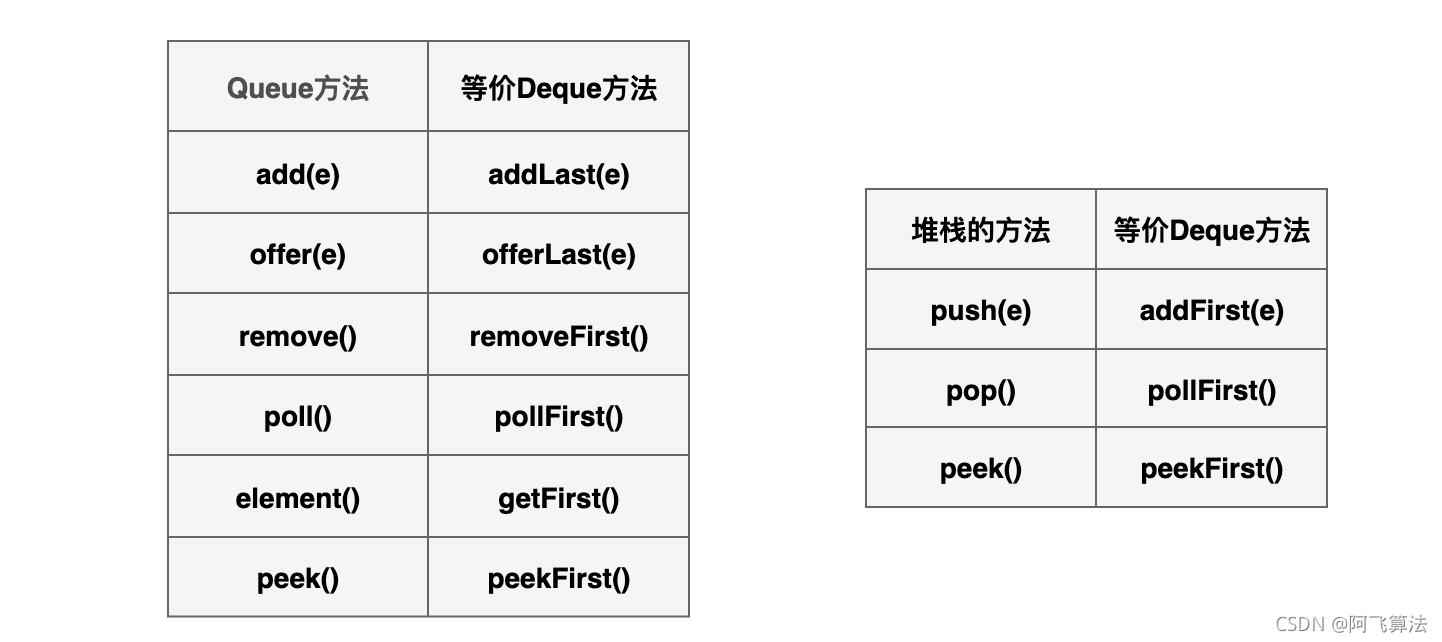
Deque的实现：

• 一般场景
  • LinkedList 大小可变的链表双端队列，允许元素为 null
  • ArrayDeque 大下可变的数组双端队列，不允许 null
• 并发场景
  • LinkedBlockingDeque 如果队列为空时，获取操作将会阻塞，知道有元素添加

Demo示例

    private static void dequeTest() {
        Deque<String> deque = new LinkedList<String>();
        deque.push("a");
        deque.push("b");
        deque.push("c");
        System.out.println(deque);
        //获取栈首元素后，元素不会出栈
        String str = deque.peek();
        System.out.println(str);
        System.out.println(deque);
        while (deque.size() > 0) {
            //获取栈首元素后，元素将会出栈
            System.out.println(deque.pop());
        }
        System.out.println(deque);
    }
//
[c, b, a]
c
[c, b, a]
c
b
a
[]
  
    private static void dequeTest1() {
        Deque<Integer> deque = new LinkedList<>();
        deque.offer(1);
        deque.offer(2);
        deque.offer(3);
        System.out.println(deque);
        Integer in = deque.peek();
        System.out.println(in);
        System.out.println(deque);
        while (deque.size() > 0) {
            System.out.println(deque.pop());
        }
        System.out.println(deque);
    }  
  
//
[1, 2, 3]
1
[1, 2, 3]
1
2
3
[]

方法1：双端队列

public int[] maxSlidingWindow(int[] nums, int k) {
    if (nums == null || nums.length == 0) return new int[]{};
    int n = nums.length;
    Deque<Integer> deque = new LinkedList<>();
    int[] ans = new int[n - k + 1];
    int index = 0;
    for (int i = 0; i < n; i++) {
        while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
            deque.pollLast();
        }
        deque.addLast(i);
        if ((i - k) == deque.peekFirst()) {
            deque.pollFirst();
        }
        if (i >= k - 1) {
            ans[index++] = nums[deque.peekFirst()];
        }
    }
    return ans;
}

方法2：双端队列

public int[] maxSlidingWindow(int[] nums, int k) {
            if (nums == null || nums.length == 0) return new int[]{};
            int n = nums.length;
            int[] res = new int[n - k + 1];
            int idx = 0;
            Deque<Integer> q = new LinkedList<>();//存的是元素的下标索引
            for (int i = 0; i < n; i++) {
                //队列中有元素，但是元素的下标已经过期，即不在k的滑窗范围内，开始从进队的First位置移除过期的索引
                while (!q.isEmpty() && q.peek() < i - k + 1) {
                    q.poll();//pollFirst()
                }
                //队列中有元素，但是队列的last位置的索引的值，小于当前的nums[i]的值，last位置的索引是无意义的，可以提前弹出
                while (!q.isEmpty() && nums[q.peekLast()] < nums[i]) {
                    q.pollLast();
                }
                //加入当前索引
                q.offer(i);
                //一定要满足滑窗的条件的时候，开始收集
                if (i >= k - 1) {
                    res[idx++] = nums[q.peek()];//peekFirst()
                }
            }
            return res;
        }

方法3：辅助数组+贪心

国际站看的的一个思路，很赞

如上图:

1.将源数组按k的大小分，最后一组不够k的话，维持现状

2 1 3 4 | 6 3 8 9 | 10 12 56

2.1.遍历数组，组装left_max，即从左开始，每个k组从左开始，取最大值

2 2 3 4 | 6 6 8 9 | 10 12 56

2.2.遍历数组，组装right_max，即从右开始，每个k组从右开始，取最大值

2 | 6 6 6 6 | 10 10 10 10 | 56 56 

3.借助左右辅助数组拼装结果数组，Math.max(right_max[i], left_max[i + k - 1])

4, 6, 6, 8, 9, 10, 12, 56

实现

 public int[] maxSlidingWindow(int[] nums, int k) {
            if (nums == null || nums.length == 0) return new int[]{};
            int n = nums.length;
            int[] left_max = new int[n];
            int[] right_max = new int[n];
            left_max[0] = nums[0];
            right_max[n - 1] = nums[n - 1];
            for (int i = 1; i < n; i++) {
                left_max[i] = (i % k == 0) ? nums[i] : Math.max(nums[i], left_max[i - 1]);
                int j = n - i - 1;
                right_max[j] = (j % k == 0) ? nums[j] : Math.max(nums[j], right_max[j + 1]);
            }
            int[] res = new int[n - k + 1];
            for (int i = 0, j = 0; i + k <= n; i++) {
                res[j++] = Math.max(right_max[i], left_max[i + k - 1]);
            }
            return res;
        }

上述贪心的证明：

思路来源国际站，很赞的一个证明

假设$a_0$,$a_1$,$a_2$ … $a_n$的窗口宽度是$w$,目标是为了获取一个$d[]=int[n-w+1]$

将上面的数组从左边开始分，每个元素的形式:$i\ast w+j$,其中$i$是从左边开始数，窗口的$index$，$j$是在这个窗口下的偏移量，其中$0<=i<=n/w$, $0<=j<=w$

构建如下的结果：

$d[i\ast w+j]=max(a[i\ast w+j+x])$这里的$x$满足：$0<=x<=w$,因此，$i\ast w+j$实际上代表的是要计算的最大值

假设有如下的数组：

$left[i\ast w+j]=left\_max(a[i\ast w+k])$​ 其中$0<=k<j$​

$right[i\ast w+j]=right\_max(a[i\ast w+k])$ 其中$j<=k<=(i+1)\ast w-1$

数组$left[]$是从左到右的每个窗口最大值

数组$right[]$是从右到左的每个窗口的最大值

有如下的推导：
$d[i\ast w+j]=max(right[i\ast w+j],left[(i+1)\ast w+j-1])$
$d[i\ast w+j]=max(right[i\ast w+j],left[(i\ast w+w+j-1])$
=>
$d[m]=max(right[m],left[m+w-1])$

结果数组$d[]$​的最后一个元素是:$d[n-w]=max(right[n-w],left[n-1])$​