分数阶域中的埃尔莫尔延迟

分数阶域中的埃尔莫延迟

Ahmed Soltana, Ahmed G. Radwanb,c, Alex Yakovlevaa英国纽卡斯尔大学电气与电子工程学院,b 埃及吉萨开罗大学工程学院工程数学与物理系, 12613,c埃及开罗尼罗河大学纳米电子集成系统中心（NISC） 邮箱: ahmed.abd-el-aal@ncl.ac.uk, agradwan@ieee.org, 和 Alex.Yakovlev@newcastle.ac.uk

摘要

互连设计最近已成为影响电路延迟和性能的重要因素之一，尤其是在深亚微米技术中。互连建模通常基于使用埃尔莫尔定义的延迟时间和上升时间。因此，本文提出了分数阶域中埃尔莫尔延迟时间和上升时间的通用公式。从延迟时间和上升时间的新公式中发现，这些时序值可以通过分数阶进行控制或调节。因此，分数阶可以补偿元件值。此外，本文研究了一个并联补偿电路的案例研究，以展示分数阶对延迟时间的影响。通过MATLAB分析，研究了元件值以及分数阶对新时序定义的影响。

关键词 —分数阶微积分；埃尔莫尔延迟时间；埃尔莫尔上升时间；传输线；互连

I. 引言

超大规模集成电路技术的进步使得片上系统能够集成极高规模的集成电路。实际上，随着技术尺寸不断缩小，互连延迟已成为主要延迟来源[1, 2]。因此，互连性能在电路的时序和功耗性能中成为至关重要的因素。一种建模互连响应的方法是采用精确的互连模型和信号传播特性来模拟互连的响应[1,3] 。这通过在树状模型中使用RLC模型来模拟不同节点响应[4, 5, 6]实现。尽管该模型能提供良好的结果，但其精度随技术尺寸缩小而下降，同时复杂性也增加。

另一方面，最近一些基于分数阶微积分的互连建模研究已经开始 [7, 1]。分数阶微积分用于描述具有无限记忆的系统，而整数阶微积分则使用有限记忆来描述系统 [8]。因此，分数阶微积分被用于在农业 [9] 和混沌系统 [10] 等多个学科中对现实世界现象进行建模。

此外，传统电路理论中的许多基本原理，如滤波器、振荡器和稳定性技术，已被推广到分数阶域 [11, 12, 13, 14]。黎曼‐刘维尔定义的阶次为 ߙ 的分数阶导数由 [8] 给出：

$$
D^\alpha f(t) \coloneqq
\begin{cases}
\frac{1}{\Gamma(m - \alpha)} \frac{d^m}{dt^m} \int_0^t \frac{f(\tau)}{(t - \tau)^{\alpha + 1 - m}} d\tau, & m−1 < \alpha < m, \
\frac{d^m}{dt^m} f(t), & \alpha = m.
\end{cases}
\tag{1}
$$

其中 $0 < \alpha < 1$，由(1)式的拉普拉斯变换可得，分数阶元件的阻抗表示为：
$$
Z(s) = k_o s^\alpha
\tag{2}
$$
其中 $k_o$ 为常数，且为分数阶。因此，文献[7, 1]中提出了基于分数阶元件而非传统元件的互连分数阶模型。实际上，这些分数阶模型通过引入分数阶的影响，解决了传输线的非线性响应问题。因此，分数阶的建模工作比整数阶域中的建模更为准确。

大多数传输线建模工作基于埃尔莫尔对延迟时间和上升时间的定义。在[15]中，埃尔莫尔提出了一种根据线性系统的传递函数计算传播延迟的通用方法。埃尔莫延迟之所以流行，主要是因为其存在一个简单且可处理的延迟公式，该公式具有递归特性，使得即使在大型电路中也能高效地计算电路延迟[16]。然而，[15]中的公式在计算信号上升和下降斜率时基于整数阶微积分。因此，这可能是互连分数阶模型不准确的原因。因此，应将埃尔莫尔对延迟时间和上升时间的定义推广到分数阶域。本工作的目的是将埃尔莫尔关于延迟和上升时间的定义推广到分数阶域。这将修改上升时间和延迟时间，以包含分数阶对互连时序的影响。此外，分数阶可用于在特定时间内优化系统延迟‐上升时间。因此，在第二节中介绍了埃尔莫延迟‐上升时间的分数阶分析。然后，在第三节中讨论了并联补偿电路的案例研究，最后在第四节给出结论。

II. 所提出的分析

具有有限个不同阶次集总分数阶元件的稳定系统的归一化系统函数为：

$$
H(s) = \frac{1 + a_1 s^{\alpha_1} + a_2 s^{\alpha_2} + \cdots + a_n s^{\alpha_n}}{1 + b_1 s^{\beta_1} + b_2 s^{\beta_2} + \cdots + b_m s^{\beta_m}}
\tag{3}
$$

其中系数 $a_i$、$b_i$、$\alpha_i$ 和 $\beta_i$ 为实数且 $\beta_m > \alpha_n$。因此，该分数阶系统对单位阶跃函数 $u(t)$ 的归一化瞬态响应可通过分数阶逆拉普拉斯变换[8]求得。另一方面，埃尔莫尔定义的延迟时间（$T_D$）是指响应达到其最终值一半所需的时间，如图1所示。此外，上升时间（$T_R$）是指达到响应曲线在半幅值点处切线斜率的倒数所对应时刻所需的时间，如图1所示。于是，延迟时间和上升时间均由下式给出：

$$
T_D = \int_0^\infty t v’(t) dt \tag{4.a}
$$
$$
T_R = \left{ 2\pi \left[ \int_0^\infty t^2 v’(t) dt - T_D^2 \right] \right}^{0.5} \tag{4.b}
$$

其中 $v’(t)$ 是瞬态电压的导数。(4)式的定义假设了整数阶积分，因此基于使用传统的整数阶元件 ${R, L, C}$。此外，在上升时间的斜率计算中，未考虑分数阶元件的分数阶 $\alpha$ 的影响，尽管它预期会对响应斜率[11]产生很大影响。因此，使用(4)式来确定采用分数阶元件的系统的时序响应是不正确的，因为这些公式忽略了分数阶的影响。

另一方面，系统函数 $H(s)$ 与瞬态响应 $e’(t)$ 通过直接拉普拉斯变换相关联，如式(5)所示：

$$
H(s) = \int_0^M E_\alpha(-s^\alpha t^\alpha) e’(t) dt^\alpha
\tag{5}
$$

其中 $E_\alpha(z)$ 是由下式给出的Mittag‐Leffler函数

$$
E_\alpha(z) = \sum_{k=0}^\infty \frac{z^k}{\Gamma(\alpha k + 1)}
\tag{6}
$$

因此，通过将拉普拉斯积分（5）展开为 $s$ 的幂级数，这将在 $s$ 位于收敛圆 $|s| = |s_1|$ 内时成为 $H(s)$ 的有效展开。因此，(3)式的传递函数可表示如下：

$$
H(s) = 1 - \int_0^\infty \frac{(st)^\alpha}{\Gamma(\alpha + 1)} e’(t) dt^\alpha + \int_0^\infty \frac{(st)^{2\alpha}}{\Gamma(2\alpha + 1)} e’(t) dt^\alpha + \cdots
\tag{7}
$$

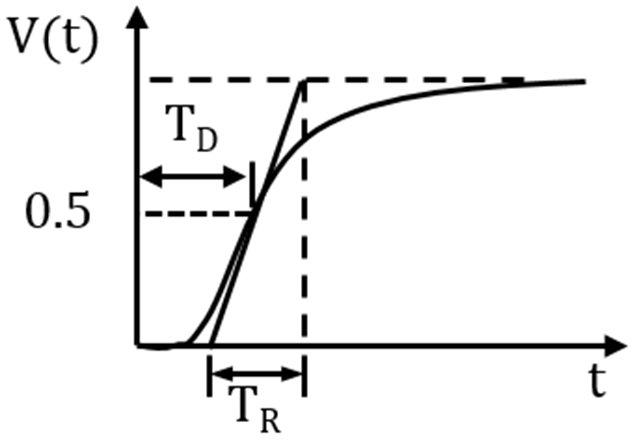
曲线显示了埃尔莫尔上升和延迟时间的原始定义。

事实上，由(7)式可得到延迟和上升时间的新定义如下：

$$
T_D = \int_0^\infty t^\alpha e’(t) dt^\alpha \tag{8.a}
$$
$$
T_R = \left( 2\pi \left[ \int_0^\infty t^{2\alpha} e’(t) dt^\alpha - T_D^2 \right] \right)^{0.5} \tag{8.b}
$$

实际上，(8) 的定义是 (4) 中埃尔莫尔时序定义的通用表达式。需要注意的是，(8) 的定义依赖于分数阶 $\alpha$。因此，在使用 (8) 公式时，分数阶延迟对系统时序的影响已被包含在内。此外，当令 $\alpha = 1$ 时，(8) 的公式与 (4) 的公式相同，从而验证了该分析。

为简化分析，假设(3)中的分数阶依赖于实数值 $\alpha$，其中 $\alpha_i = i\alpha$、$\beta_j = j\alpha$ 和 $i = 1…n$ 以及 $j = 1…m$。因此，(3)的传递函数可重写如下：

$$
H(s) = \frac{1 + a_1 s^\alpha + a_2 s^{2\alpha} + \cdots + a_n s^{n\alpha}}{1 + b_1 s^\alpha + b_2 s^{2\alpha} + \cdots + b_m s^{m\alpha}}
\tag{9}
$$

通过展开传递函数(9)，然后近似到二阶分量，可得到式(8)中的延迟和上升时间定义：

$$
T_D = \Gamma(\alpha + 1)(b_1 - a_1) \tag{10.a}
$$
$$
\frac{T_R^2}{\pi^2} = \Gamma(2\alpha + 1)(a_2 - b_2 - b_1(a_1 - b_1)) - T_D^2 \tag{10.b}
$$

其中 $\Gamma$ 是由 [8] 给出的伽马函数：

$$
\Gamma(x) = \int_0^\infty z^{x-1} e^{-z} dz
\tag{11}
$$

由(10)可知，延迟和上升时间是分数阶 $\alpha$ 的函数。通过代入分数阶 $\alpha = 1$，(10)中的延迟定义便等同于[15]中的延迟和上升时间表达式。因此，(10)中的时序表达式是分数阶域中埃尔莫尔延迟定义的通用形式。

此外，分数阶 $\alpha$ 对上升时间和延迟时间的影响分别如图2 (a, b) 所示。对于 $\alpha < 1$，延迟时间相对于 $\alpha$ 的变化非常小。另一方面，上升时间随分数阶 $\alpha$ 的变化较大。因此，如图2所示，脉冲的上升时间可以独立控制而不影响脉冲的延迟时间。这增加了设计自由度和灵活性。此外，埃尔莫尔时间公式的特性在 $\alpha > 1$ 时表现为电容效应，在 $\alpha < 1$ 时表现为电感响应。这是因为随着 $\alpha$ 值的增加，延迟时间和上升时间均增加，意味着电容效应对系统时序性能的影响增强。当 $\alpha < 0.33$ 时，上升时间和延迟时间没有取值，因为系统不稳定，因此在此范围内 $T_R$ 和 $T_D$ 在 $a_1 = b_2 = 0.25$、$a_2 = 0$ 以及 $b_1 = 1$ 时无有效解。

此外，图3展示了在不同分数阶 $\alpha$ 值下 $b_1$ 变化对埃尔莫延迟的影响。

(a) 当 $a_1 = b_2 = 0.25$, $a_2 = 0$ 和 $b_1 = 1$ 时，延迟时间随分数阶 $\alpha$ 的变化情况

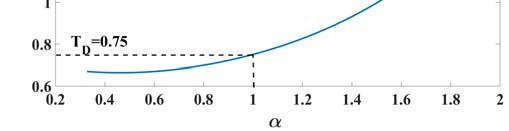
(b) 当 $a_1 = b_2 = 0.25$, $a_2 = 0$ 和 $b_1 = 1$ 时，上升时间随分数阶 $\alpha$ 的变化情况

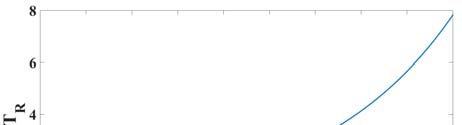
$\alpha$ 和 $b_1$ 对上升时间（$T_R$）在 $a_1 = b_2 = 0.25$, $a_2 = 0$ 处的影响

III. 案例研究

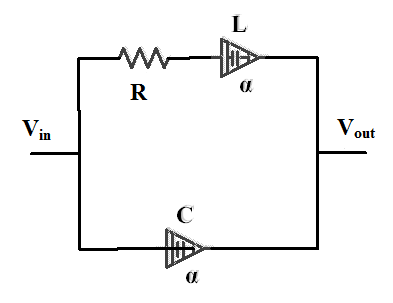
将埃尔莫延迟的分数阶模型应用于图4所示的并联模型，以验证所提出模型的可靠性。该电路的传递函数为：

$$
G(s) = \frac{R}{1 + s^\alpha RC + LC s^{2\alpha}} \cdot \frac{1}{1 + s^\alpha L/R}
\tag{12}
$$

因此，参数 $a_1$、$b_1$、$b_2$ 如下所示：

$$
a_1 = \frac{L}{R},\quad b_1 = RC,\quad b_2 = LC
\tag{13}
$$

因此，根据(10)和(13)，埃尔莫尔上升和延迟时间由下式给出：

$$
T_D = \Gamma(\alpha + 1) \left( R^2 C - L \right) / R
\tag{14.a}
$$
$$
T_R^2 = 2\pi \left{ \Gamma(2\alpha + 1)(-2LC + R^2 C^2) - T_D^2 \right}
\tag{14.b}
$$

由(14)式可得，当 $\alpha = 1$、$R = C = 1$ 和 $L = 1/4$ 时，对应于临界并联补偿，$T_D = 3/4$ 和 $T_R = 1.66$，这与[15]中计算得到的值相同。因此，(14)式的定义是分数阶域中并联补偿延迟的通用表示。

由(14)可知，上升时间与延迟时间之间的关系相对于电路参数和分数阶 $\alpha$ 呈非线性。在分数阶 $\alpha$ 较大时，延迟时间随电容的变化非常明显。另一方面，对于 $\alpha < 1$，电容 $C$ 对延迟时间的影响非常小，如图5(a)中的 MATLAB分析所示。此外，分数阶 $\alpha$ 和电感 $L$ 对延迟时间的影响如图5(b)所示。当电感 $L$ 较小时，随着 $\alpha$ 的增加，延迟时间增加。此外，对于相同的 $\alpha$ 值，延迟时间随电感的增加而减小。从图5可以看出，对于不同阶次下的所有电感或电容值，延迟时间并非都具有有效值。这意味着，并联补偿电路在这些点上是不稳定的。实际上，分数阶 $\alpha$ 可以为系统增加另一个自由度。

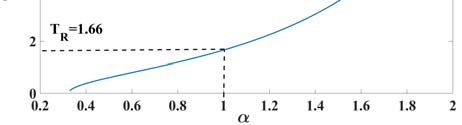
采用相同分数阶的分数阶电感和电容进行并联补偿 $\alpha$

分数阶可用于补偿元件影响以实现特定延迟时间的延迟公式。换句话说，系统可针对特定延迟时间进行设计，同时元件值的变化最小。

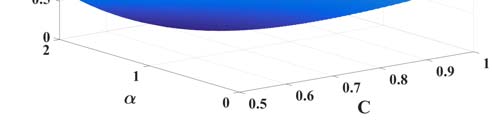
上升时间与延迟时间随 $C$、$L$ 以及分数阶 $\alpha$ 的变化非常相似，分别如图6 (a, b)所示。对于相同的电容值，上升时间随着分数阶 $\alpha$ 的增加而增加。此外，对于相同的电容值，上升时间也随着分数阶的增加而增加。因此，为了获得较小的上升时间值，应使用较小的电容值和较低的阶次。然而，如图6(a)所示，上升时间并非在所有分数阶 $\alpha$ 和 $C$ 的组合下都具有有效值。因此，可以通过调节分数阶 $\alpha$ 来设计系统以满足特定的上升时间要求。

通过比较图6 (a, b)，在相同的分数阶值下，电感对上升时间的影响大于电容对上升时间的影响。这意味着，对于相同的阶次，通过改变电感和电容，上升时间也可以实现两级调节。另一方面，对于相同的分数阶值，电容和电感对延迟时间的影响非常相似，如图5 (a, b)所示。

因此，新的埃尔莫尔延迟时间和上升时间的定义通过引入分数阶的影响，增加了设计自由度。此外，分数阶可用于补偿电感或电容对上升时间或延迟时间的影响。

IV. 电路仿真

为了验证分析，本节展示了使用先进设计系统（ADS）对图4所示电路进行的电路仿真。分数阶元件通过 [17]的梯形网络实现。该电路采用相同的电阻、电容和电感值，但在不同分数阶次下进行仿真，以显示分数阶对延迟和上升时间的影响。当电容的阶次低于理想情况时，电路响应具有更大的延迟，如图7所示。

(a) 在 $R = 1\ \Omega$、$L = 0.25\ H$ 条件下延迟时间随 $\alpha$ 和 $C$ 的变化

(b) 在 $R = 1\ \Omega$、$C = 1\ F$ 处延迟时间相对于 $\alpha$ 和 $L$ 的变化

(a) 在 $L = 0$、$R = 1\ \Omega$、$25\ H$ 时上升时间随 $\alpha$ 和 $C$ 的变化

(b) 在 $R = 1\ \Omega$，$C = 1\ F$ 时上升时间随 $\alpha$ 和 $L$ 的变化

而对于使用传统电容的仿真，其响应与理想响应相同。因此，在电路中使用分数阶电容可使电路响应非常接近实际互连响应。此外，如图7所示，在模型中使用分数阶电感可改善电路的上升时间和延迟时间。因此，分数阶电感可与互连集成以改善其响应。

针对图 4 电路的电路仿真，参数值相同，但阶次不同：$R = 10\ \Omega$，$L = 37\ \mu H$，$C = 10\ nF$

V. 结论

本文提出了一种分数阶域中埃尔莫尔延迟时间和上升时间的新定义。所提出的公式在计算上升时间和延迟时间时考虑了分数阶的影响。通过在时序公式中引入分数阶，增加了另一个自由度，从而提高了设计灵活性并拓宽了优化空间。最后，对具有两个同阶次分数阶元件的并联补偿进行了案例研究。根据MATLAB分析，仅通过改变分数阶次而不影响元件值，即可针对特定数值优化并联补偿的时序。

未来的工作将涉及将分析数据与我们最近送交制造的实际物理传输线的表征进行比较。