文章目录
一、课本概念及公式
3.1 平面图及其平面嵌入
平面图的定义
3.2 平面图欧拉公式
公式
3.3 极大平面图
面的次数和桥的概念
平面图的各个面的边数和与边满足的关系
即： ∑ i = 1 ϕ d ( f i ) = 2 ε \sum_{i=1}^{\phi} d\left(f_{i}\right)=2 \varepsilon ∑i=1ϕd(fi)=2ε
推论3.1
证明：
若非连通图时，可以分成多个连通片，有：
推论3.2
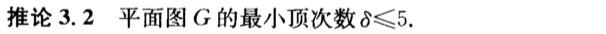
证明：
由 ： { ε ⩽ 3 ν − 6 ∑ v ∈ V ( G ) d ( v ) = 2 ε ∑ v ∈ V ( G ) d ( v ) ⩾ δ ν 由：\left\{\begin{array}{c} \varepsilon \leqslant 3\nu-6 \\ \sum_{v \in V(G)} d(v)=2 \varepsilon \\ \sum_{v \in V(G)} d(v) \geqslant \delta \nu \end{array}\right. 由：⎩⎨⎧ε⩽3ν−
最低0.47元/天 解锁文章
扫一扫
3262
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
