卷积

先验知识：卷积神经网络、数字图像处理、数字信号处理

前言

卷积神经网络（Convolutional Neural Networks，CNN）由卷积、采样和非线性函数组成，其中图像中的卷积定义了一个固定大小的卷积核在图像空间域进行参数滤波（线性运算），图像中的卷积为什么是定义一个固定大小的核在图像中进行扫描？（实际的操作是矩阵相乘）

大纲

• 信号处理中卷积的定义

• 相关和卷积的关系

• 图像中卷积的实现（搜狗算法研究助理面试题）

信号处理中卷积的定义

1. 卷积定义

卷积的连续定义如公式1，称公式1为信号f，g的卷积：

 

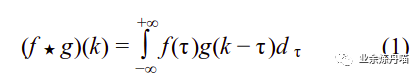
其中k是一个固定的常量，可以看到信号f和信号g的输入取值做了一个长度为k的180度翻转，卷积定义中两个信号在某个时刻的值做了一个相乘，可以理解成广义的相关性计算，为什么是广义的相关性？参考两个向量v1和v2相关性的计算，通常用cosine距离，其中cosine距离的定义如公式2：

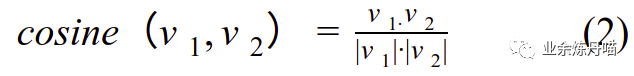
其中分母部分分别把向量v1和v2做了归一化，统一到相同的尺度。在相同尺度下的信号做点乘即是计算两个信号的相关性。公式1是两个信号的连续卷积定义，在计算机系统里面通常不能做这样的连续积分，通常将积分转换成离散求和，那么信号f和g的离散卷积定义如公式3：

两个卷积的定义都有一个共同的特点其中: t+(k-t)=k。这样的特点让相关和卷积存在一定的联系，是什么样的联系呢？先看看相关的定义。

相关和卷积的关系

1. 图像（二维）空间滤波

       在冈萨雷斯版数字图像处理[1]中介绍了图像空间滤波操作，其计算过程如下图1：

图1 图像空间滤波

用一个k×k的滤波器（滤波器中的参数如上图,k=3），从图像（图中f）的左上角进行扫描，扫描一次将w和f对应位置相乘相加：g=f(x-1,y-1)×w(-1,-1)+f(x-1,y)×w(-1,0)...f(x+1,y+1)×w(1,1)。将g赋给f(x,y)，遍历整个图像完成滤波操作。在执行线性空间滤波时，必须清楚理解两个相近的概念：相关和卷积[1]。上述过程是相关定义。

2. 相关和卷积的关系

       从公式3离散卷积的定义知道，去掉常量k，公式3计算的就是两个信号的广义相关性，那么卷积就是将计算相关性的滤波器进行翻转180度再滤波。相关和卷积的关系如图2：

图2 相关和卷积的关系

但是目前的深度学习框架里面并没有对卷积核进行翻转180度，其实我们可以这样去理解当前初始化的卷积核是某个相关核进行翻转后的结构，那么卷积我个人理解也是一种相关性计算（不赞同可以后台留言哟）。

图像中卷积的实现

1. 深度学习框架（TensorFlow为例）中卷积的实现

       前面分析了图像中卷积的计算过程，那么在深度学习框架中是否是按照这样的方式进行，我们可以粗略的计算对一张宽高分别是W和H的图像进行一次卷积（卷积核大小K×K）的时间复杂度：O（W×H×K×K）。这样的时间复杂度似乎比较高，举个例子：假设输入一张彩色图像X，该图像由RGB三个通道组成，每个通道的宽和高分别用W和H表示，想通过卷积产生Cout张Feature Map（默认具备CNN相关知识），输入X的维度是（B,Cin,Win,Hin），其中B、Cin、Win和Hin分别表示输入的BatchSize、Channel、Width和Height。那么想要得到的输出Y的维度是（B,Cout,Wout,Hout）。如果用上述计算方式时间复杂度变成O（Cin×Cout×W×H×K×K），这样的时间复杂度似乎并不高效，那么深度学习框架里面卷积是如何实现的呢？一TF为例，TF对操作的数据称为Tensor，那么将输入和输出都转换成Tensor，现在卷积的目标是将Tensor X(B,Cin,Win,Hin)转换成Y(B,Cout,Wout,Hout)。

       查阅了TF的相关API可以得到如图3关于二维卷积的计算过程：

图3 TensorFlow中二维卷积的计算过程[2]

    二维卷积中卷积在输入Cin个通道上的卷积核大小是filer_height×filter_width×Cin，是一个三维的卷积核，一次卷积产生一个feature map，该卷积核中的参数大小是filer_height×filter_width×Cin，那么Cout个feature map就有Cout个卷积核，将卷积核reshape成(filer_height×filter_width×Cin,Cout)。由输入Tensor维度和卷积核大小可以计算每个feature map的宽和高。因此可以计算输出的Tensor维度(B,Cout,Wout,Hout)。将输入Tensor(B,Cin,Win,Hin)提取每个卷积操作的patch（filter_height,filter_width），组成新的virtual tensor，那么这样的patch一共有Wout×Hout个，每个patch的维度filer_height×filter_width×Cin，那么Virutal Tensor维度（B,Wout,Hout,filer_height×filter_width×Cin），将Virtual Tensor进行reshape到维度（B×Wout×Hout,filer_height×filter_width×Cin）将卷积核（filer_height×filter_width×Cin,Cout）右乘Virtual Tensor得到输出的维度（B×Wout×Hout，Cout）再reshape成（B,Cout,Wout,Hout)从而实现了卷积运算，感兴趣可以计算一下时间复杂度。

[1] 冈萨雷斯.《数字图像处理》

[2] https://www.tensorflow.org/api_docs/python/tf/nn/conv2d