RNN循环神经网络之原理详解

原创已于 2025-06-06 19:33:54 修改 · 1k 阅读

32 ·

CC 4.0 BY-SA版权

文章标签：

#rnn #人工智能 #深度学习

于 2025-01-26 21:30:45 首次发布

一、为什么要提出RNN

在进行CNN、DNN等神经网络训练时，训练数据都默认为是“独立同分布”的。但是有些数据，如一段话、股票数据等，是有先后顺序的。因此，数据规律除了与数据分布相关外，也与数据之间的先后关系有关。为此，就提出了RNN循环神经网络，在传统DNN网络的基础上，加入了学习数据先后关系的能力。

二、什么是RNN

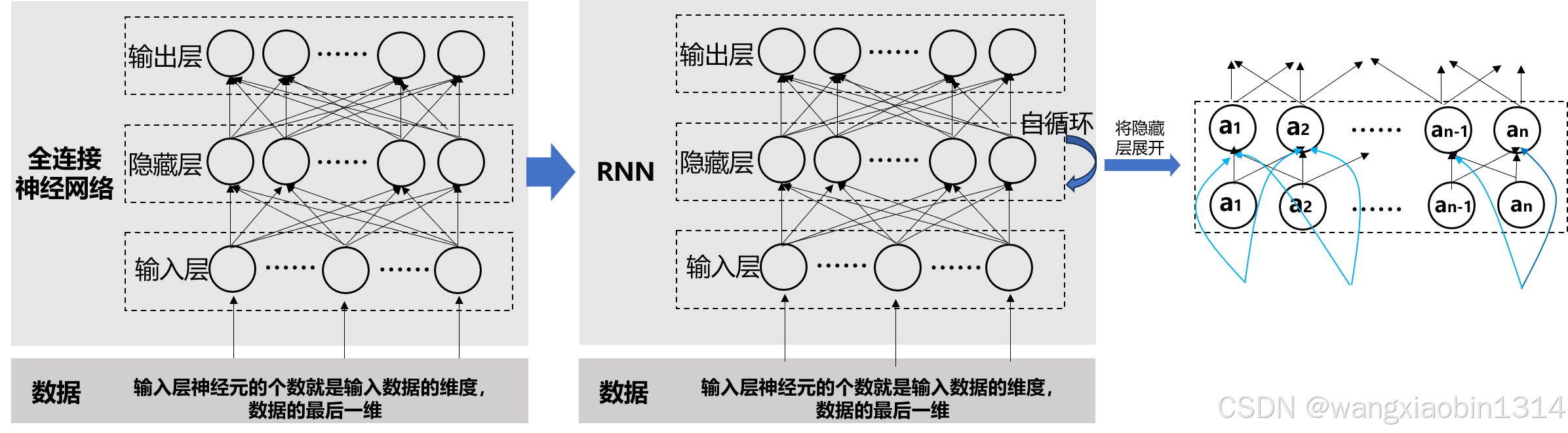
RNN与DNN最大的区别在于隐藏层：DNN的隐藏层的输入是由输入层经过线性变换（矩阵相乘），然后再经过一个激活函数（如sigmoid，ReLu）变换后的结果。而RNN的隐藏层除了接收输入层的数据外，还得叠加一个隐藏层的自输入（隐藏层节点进行矩阵相乘），然后再加一个激活函数（如sigmoid，ReLu）变换后的结果。

由于隐藏层需要自输入，因此，引入了一个问题：隐藏层的节点需要有初始值（初始化），还得根据接收的输入数据进行更新。如何进行更新呢？详见下文2.1。

2.1、RNN前向传播

假设我们输入的数据是一段文字，例如：“我爱北京天安门”。由于神经网络无法处理文字，需要我们将文字转换为数字，可以有one-hot方法或embedding。这里以embedding为例，假设经过训练后，“我”的词向量为[0.1,0.2,0.3,0.18,0.11]，“爱”的词向量为[0.2,0.1,0.4,0.55,0.18]，“北京”的词向量为[-0.1,0.3,0.12,0.55,0.51]，“天安门”的词向量为[0.33,0.44,0.55,0.66,0.77]。那么，输入数据X为：

如果是DNN，那么可以将这些数据一次性输入进去，DNN是无法分析出“我”、“爱”、“北京”、“天安门”这几次词之间的先后顺序的。对DNN来说，数据的先后输入顺序是不影响结果的，甚至还得在输入前将数据打乱shuffle。

如果是RNN，那么需要先输入“我”对应的词向量，然后再输入“爱”对应的词向量，以此类推......因此，RNN存在一个弊端就是无法并行计算。

回到上文遗留的问题，由于隐藏层需要自输入，就涉及到隐藏层的初始化值及更新方式。假定隐藏层的神经元个数为3，隐藏层的初始化值假设为h0=[A1,A2,A3]=[0,0,0]，输出为2分类问题，网络结构如下：

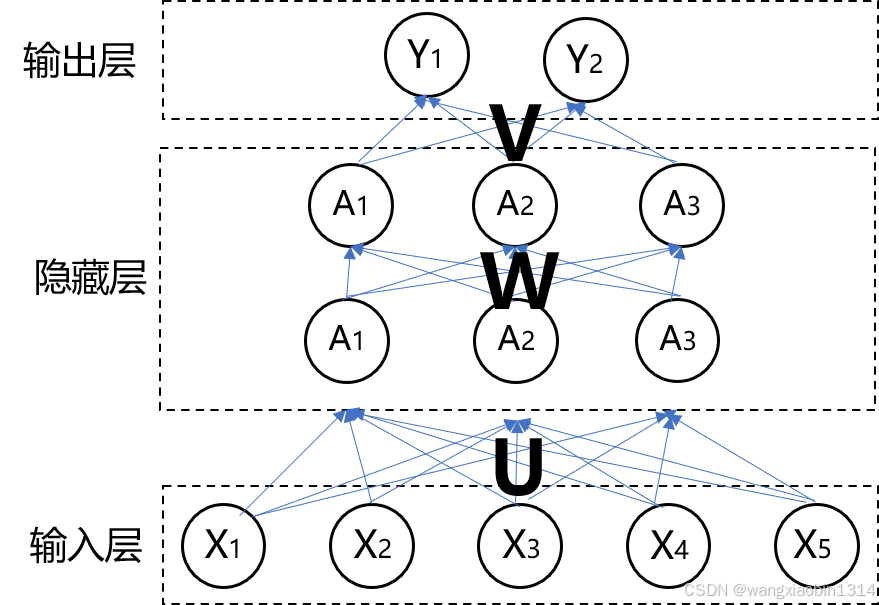
用矩阵U表示输入层与隐藏层之间的权重矩阵；W表示隐藏层自输入权重矩阵，V表示隐藏层与输出层之间的矩阵。

2.1.1 输入“我”对应的词向量时

隐藏层节点A1的值由两部分组成：

一部分是来自于输入层的数据：
另一部分是来自于隐藏层自输入：
因此，
A1用矩阵乘法表示为：

同理，隐藏层节点A2的值用矩阵乘法计算为：

隐藏层节点A3的值用矩阵乘法计算为：

那么A1、A2、A3的值更新,用矩阵乘法表示为：

再加上激活函数，用矩阵乘法表示为：

其中，f为激活函数。h1为输入“我”后隐藏层对应的输出值。

输出层Y1的值为：，用矩阵乘法表示为：

同理，输出层Y2的值用矩阵表示为：

输出层Y1、Y2可以直接进行输出，也可先经过激活函数（如softmax）后输出。

2.1.2输入“爱”对应的词向量时：

A1、A2、A3的值更新，用矩阵乘法表示为：

2.2 RNN前向传播公式总结

对于时刻t，输入数据为Xt，那么RNN的前向传播公式为:

f和g均为激活函数

2.3、RNN反向传播

还是以“我爱北京天安门”为例，由于有4个词，那么会有4个时刻的输出（当然也不是绝对的，因场景而异，例如我们去判断这句话的情感是正向的还是负向的，那只有最后一个时刻进行输出）。反向传播是将偏差往回传播，因此会有4个时刻的偏差，那么总偏差就是这四个时刻的偏差总和。以MSE为例，loss值为：，为预测输出值，为真实值