图解深度学习-梯度下降学习率可视化

梯度下降学习率问题

用最简单的SGD做实验，讨论学习率问题。

学习率如果太小，则会下降很慢，需要很多次迭代，如果太大，就会出现发散，具体可以动手调试，也可以看截图。

这里我选取的代价函数$J(x)=0.5(x-1{)}^2+0.5$，求导方便。

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import *

 
#梯度函数的导数
def gradJ(theta):
    return theta-1
 
#梯度函数
def J(theta):
    return 0.5*(theta-1)**2+0.5
 
def train(lr,epoch,theta):
    thetas = []
    for i in range(epoch):
        gredient = gradJ(theta)
        theta = theta - lr*gredient
        thetas.append(theta)
    plt.figure(figsize=(10,10))
    x = np.linspace(-1,3,100)
    plt.plot(x, J(x))
    plt.plot(np.array(thetas),J(np.array(thetas)),color='r',marker='o')
    
    plt.plot(1.0, 0.5, 'r*',ms=15)
    plt.text(1.0, 0.55, 'min', color='k')
    plt.text(thetas[0]+0.1,  J(thetas[0]), 'start', color='k')
    plt.text(thetas[-1]+0.1, J(thetas[-1])-0.05, 'end', color='k')
    
    plt.xlabel('theta')
    plt.ylabel('loss')
    plt.show()
    print('theta:',theta)
    print('loss:',J(theta))
    
#可以随时调节，查看效果 (最小值，最大值，步长)
@interact(lr=(0, 5, 0.001),epoch=(1,100,1),init_theta=(-1,3,0.1),continuous_update=False)
def visualize_gradient_descent(lr=0.05,epoch=10,init_theta=-1):
    train(lr,epoch,init_theta)

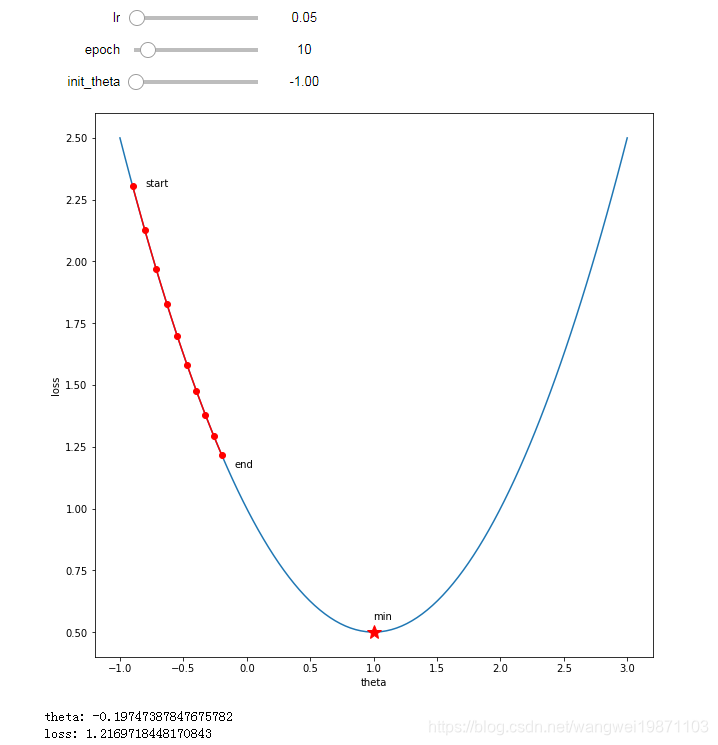
学习率:0.05
迭代次数:10
参数初始化:-1
10次迭代还没到最小值

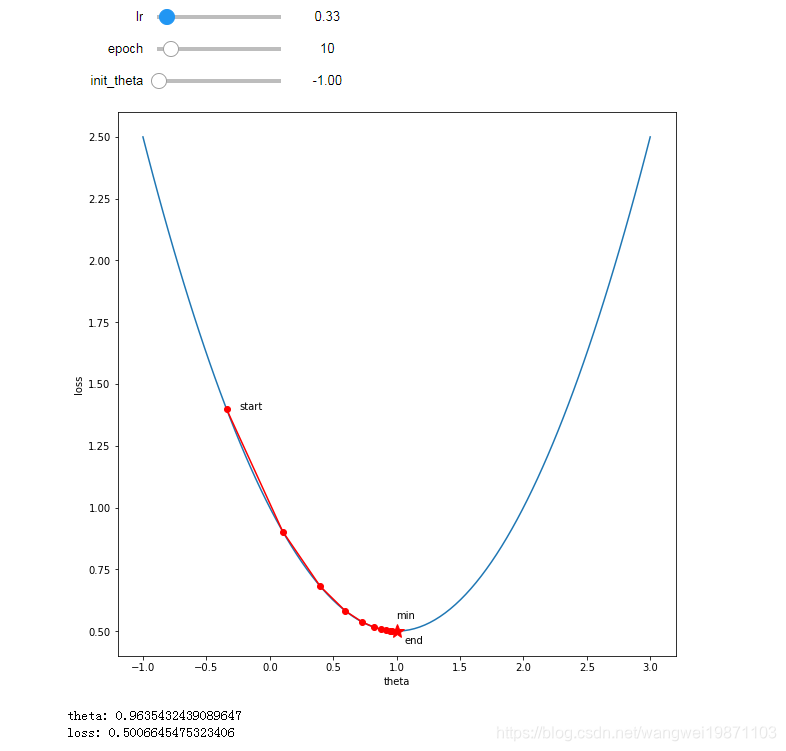
学习率:0.33
迭代次数:10
参数初始化:-1
10次迭代接近收敛了，可见加大学习率可以加快训练

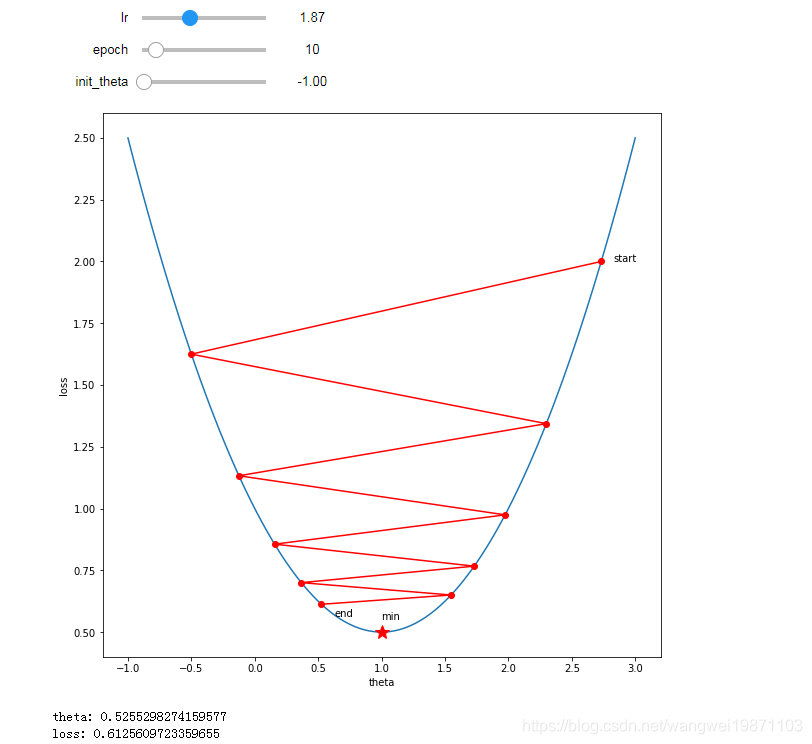
学习率:1.87
迭代次数:10
参数初始化:-1
轨迹开始波动了，梯度方向不停的在变，最后还没到收敛。

解释下梯度方向为什么开始变了，根据公式theta= theta- lr*gredient，
可以看到开始theta大致为2.7，梯度为正数大致为2，然后学习率又1.87 ，
theta=2.7 - 2 x 1.87<0 即theta变为负数了，所有到曲线右边了，
同理继续更新，此时梯度为负数了，减去一个负数等于加上正数，theta变为正数，
所以又到曲线右边，如此循环，直到最低点。
如此一来，来回波动很多次，所以收敛速度变慢了。我们当然希望它跟上面一样是从一个方向一直下降。

学习率:2.18
迭代次数:10
参数初始化:-1
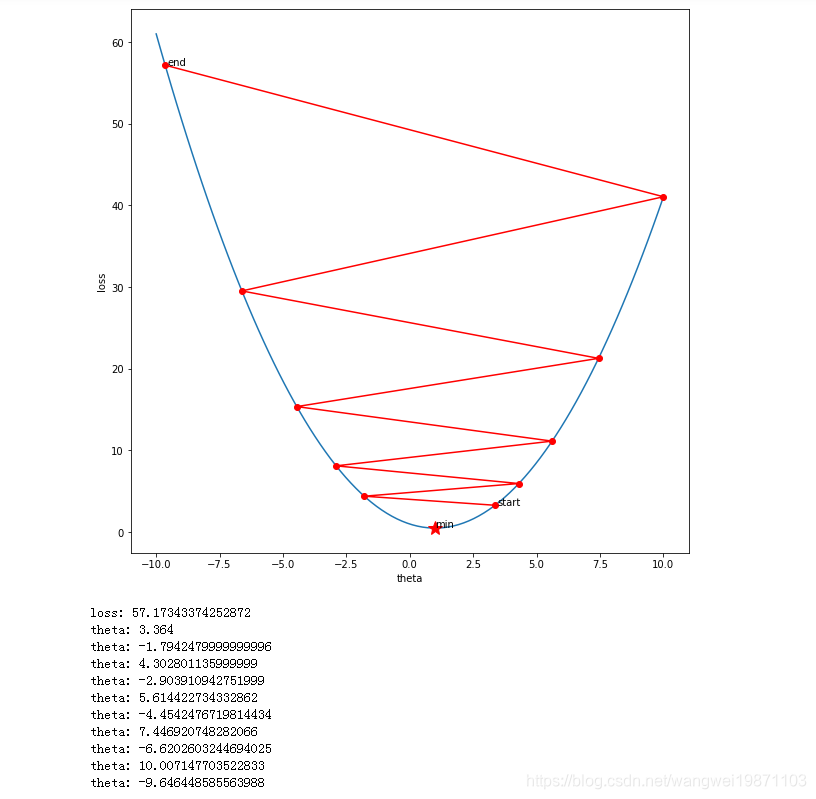
继续加到学习率，直到变得不收敛，我把坐标范围拉大了，看了清楚，已经开始发散了。

原因是因为，学习率过大，使得更新后的theta无论正负，绝对值会越来越大，会开始往上跑，再加上越上面的梯度绝对值越来越大，所以每次更新完之后theta的绝对值继续变大，就无限循环了，不收敛了。

具体可见下图。

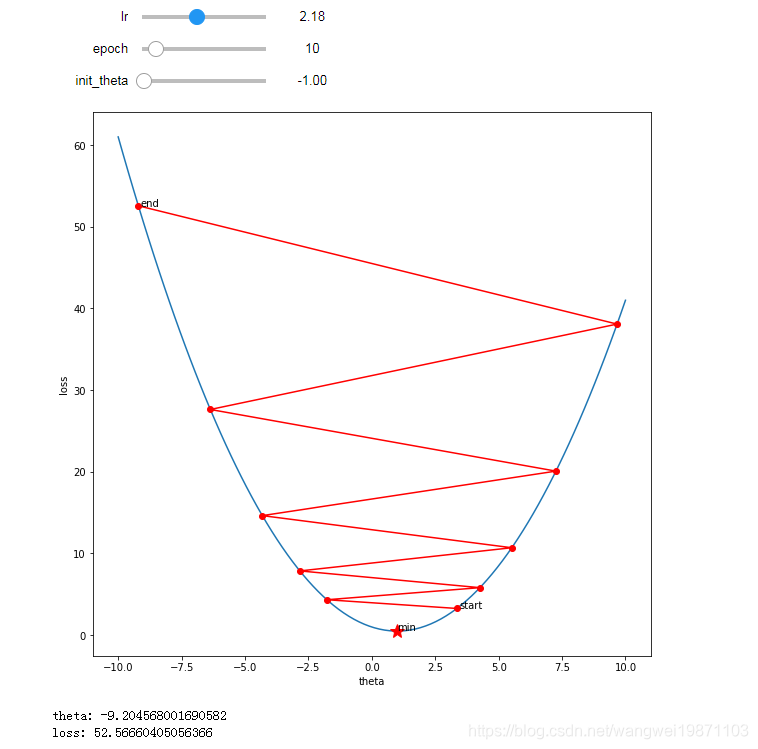
把一些参数打出来了，可以看到，负值和正值绝对值都在变大，因为迭代后出现折线发散。

修改后的jupyter的文件链接

好了，今天就到这里了，希望对学习理解有帮助，大神看见勿喷，仅为自己的学习理解，能力有限，请多包涵。