1.9 LeetCode总结（图）_图类

编程总结

每每刷完一道题后，其思想和精妙之处没有地方记录，本篇博客用以记录刷题过程中的遇到的算法和技巧

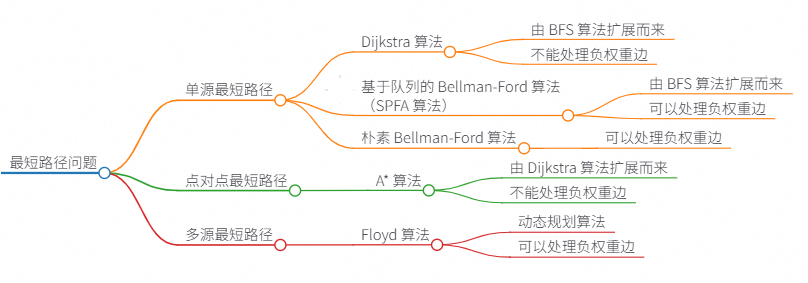
Dijkstra 算法_求最短路径

Dijkstra 算法是一种用于计算图中单源最短路径的算法，其本质是标准 BFS 算法 + 贪心思想。
如果图中包含负权重边，会让贪心思想失效，所以 Dijkstra 只能处理不包含负权重边的图。
Dijkstra 算法和标准的 BFS 算法的区别只有两个：
1、标准 BFS 算法使用普通队列，Dijkstra 算法使用优先级队列，让距离起点更近的节点优先出队（贪心思想的体现）。
2、标准 BFS 算法使用一个 visited 数组记录访问过的节点，确保算法不会陷入死循环；Dijkstra 算法使用一个 distTo 数组，确保算法不会陷入死循环，同时记录起点到其他节点的最短路径。

dijkstra 算法 同样是贪心的思路，不断寻找距离 源点最近的没有访问过的节点。

这里给出 dijkstra三部曲：
第一步，选源点到哪个节点近且该节点未被访问过
第二步，该最近节点被标记访问过
第三步，更新非访问节点到源点的距离（即更新minDist数组）

算法源码

迪杰斯特拉算法说明

/*
 * Dijkstra最短路径。
 * 即，统计图(G)中"顶点vs"到其它各个顶点的最短路径。
 * 参数说明：
 *        G -- 图
 *       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
 *     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
 *     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
 */
void dijkstra(Graph G, int vs, int prev[], int dist[])
{
    int i,j,k;
    int min;
    int tmp;
    int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
    // 初始化
    for (i = 0; i < G.vexnum; i++)
    {
        flag[i] = 0;              // 顶点i的最短路径还没获取到。
        prev[i] = 0;              // 顶点i的前驱顶点为0。
        dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
    }
    // 对"顶点vs"自身进行初始化
    flag[vs] = 1;
    dist[vs] = 0;
    // 遍历G.vexnum-1次；每次找出一个顶点的最短路径。
    for (i = 1; i < G.vexnum; i++)
    {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        min = INF;
        for (j = 0; j < G.vexnum; j++)
        {
            if (flag[j]==0 && dist[j]<min)
            {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = 1;
        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (j = 0; j < G.vexnum; j++)
        {
            tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出
            if (flag[j] == 0 && (tmp  < dist[j]) )
            {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }
    // 打印dijkstra最短路径的结果
    printf("dijkstra(%c): \n", G.vexs[vs]);
    for (i = 0; i < G.vexnum; i++)
        printf("  shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]);
}

743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n。
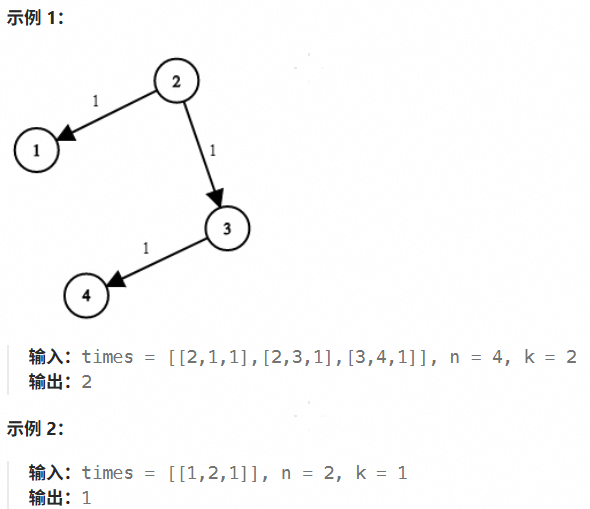
给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。
现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

int networkDelayTime(int **times, int timesSize, int *timesColSize, int n, int k)
{
    const int inf = 0x3f3f3f3f;
    int g[n][n];
    memset(g, 0x3f, sizeof(g));
    for (int i = 0; i < timesSize; i++) {
        int x = times[i][0] - 1;
        int y = times[i][1] - 1;
        g[x][y] = times[i][2]; // 权重
    }
    int dist[n]; // 记录所有节点到源点的最短路径
    memset(dist, 0x3f, sizeof(dist));
    dist[k - 1] = 0;
    int used[n]; // 标记是否访问过
    memset(used, 0, sizeof(used));
    int ans = 0;
    for (int i = 0; i < n; ++i) {
        int x = -1;
        for (int y = 0; y < n; ++y) {
            // 第一步，选源点到哪个节点近且该节点未被访问过
            if ((used[y] == 0) && (x == -1 || dist[y] < dist[x])) {
                x = y;
            }
        }
        used[x] = 1; // 第二步，该最近节点被标记访问过
        // 第三步，更新非访问节点到源点的距离（即更新minDist数组）
        ans = fmax(ans, dist[x]);
        for (int y = 0; y < n; ++y) {
            dist[y] = fmin(dist[y], dist[x] + g[x][y]);
        }
    }
    return ans == inf ? -1 : ans;
}

Bellman-ford 算法 – 权重存在负数

Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作（n为节点数量），从而求得目标最短路。

什么叫做松弛

看到这里，估计大家都比较晕了，为什么是 n-1 次，那“松弛”这两个字究竟是个啥意思？
我们先来说什么是 “松弛”。
《算法四》里面把这个操作叫做 “放松”， 英文版里叫做 “relax the edge”

所以大家翻译过来，就是 “放松” 或者 “松弛” 。

但《算法四》没有具体去讲这个 “放松” 究竟是个啥？ 网上很多题解也没有讲题解里的 “松弛这条边，松弛所有边”等等 里面的 “松弛” 究竟是什么意思？

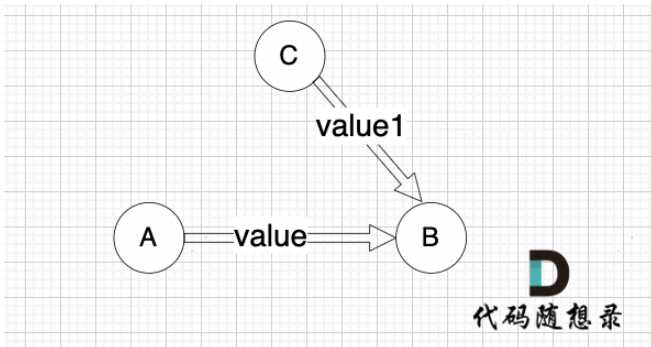
这里我给大家举一个例子，每条边有起点、终点和边的权值。例如一条边，节点A 到 节点B 权值为value，如图：

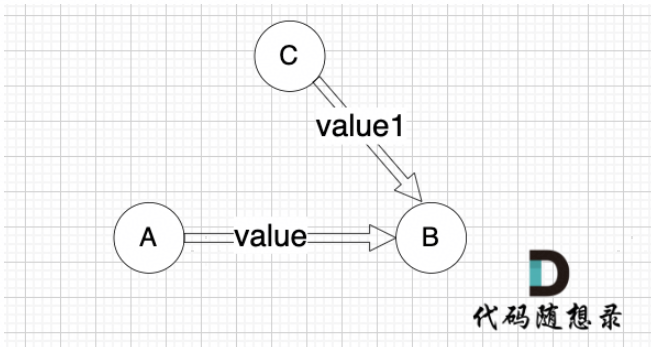
minDist[B] 表示 到达B节点 最小权值，minDist[B] 有哪些状态可以推出来？
状态一： minDist[A] + value 可以推出 minDist[B] 状态二： minDist[B]本身就有权值 （可能是其他边链接的节点B 例如节点C，以至于 minDist[B]记录了其他边到minDist[B]的权值）

minDist[B] 应为如何取舍。

本题我们要求最小权值，那么 这两个状态我们就取最小的

if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
也就是说，如果 通过 A 到 B 这条边可以获得更短的到达B节点的路径，即如果 minDist[B] > minDist[A] + value，那么我们就更新 minDist[B] = minDist[A] + value ，这个过程就叫做 “松弛” 。

Floyd 算法 – 多源最短路径算法

而本题是多源最短路，即 求多个起点到多个终点的多条最短路径。

通过本题，我们来系统讲解一个新的最短路算法-Floyd 算法。

Floyd 算法对边的权值正负没有要求，都可以处理。
Floyd算法核心思想是动态规划。

给出过动规五部曲：
确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

A* 算法 – 点对点的最优路径

Astar
Astar 是一种 广搜的改良版。 有的是 Astar是 dijkstra 的改良版。
其实只是场景不同而已 我们在搜索最短路的时候， 如果是无权图（边的权值都是1） 那就用广搜，代码简洁，时间效率和 dijkstra 差不多 （具体要取决于图的稠密）

如果是有权图（边有不同的权值），优先考虑 dijkstra。
而 Astar 关键在于 启发式函数， 也就是 影响 广搜或者 dijkstra 从 容器（队列）里取元素的优先顺序。
以下，我用BFS版本的A * 来进行讲解。
在BFS中，我们想搜索，从起点到终点的最短路径，要一层一层去遍历。

看出 A * 可以节省很多没有必要的遍历步骤。
为了让大家可以明显看到区别，我将 BFS 和 A * 制作成可视化动图，大家可以自己看看动图，效果更好。
地址：https://kamacoder.com/tools/knight.html
那么 A * 为什么可以有方向性的去搜索，它的如何知道方向呢？
其关键在于 启发式函数。
这是影响BFS搜索方向的关键。

对队列里节点进行排序，就需要给每一个节点权值，如何计算权值呢？
每个节点的权值为F，给出公式为：F = G + H
G：起点达到目前遍历节点的距离
H：目前遍历的节点到达终点的距离
起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。
本题的图是无权网格状，在计算两点距离通常有如下三种计算方式：

曼哈顿距离，计算方式： d = abs(x1-x2)+abs(y1-y2)
欧氏距离（欧拉距离） ，计算方式：d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
切比雪夫距离，计算方式：d = max(abs(x1 - x2), abs(y1 - y2))
x1, x2 为起点坐标，y1, y2 为终点坐标 ，abs 为求绝对值，sqrt 为求开根号，

选择哪一种距离计算方式 也会导致 A * 算法的结果不同。
本题，采用欧拉距离才能最大程度体现 点与点之间的距离。
所以 使用欧拉距离计算 和 广搜搜出来的最短路的节点数是一样的。 （路径可能不同，但路径上的节点数是相同的）
我在制作动画演示的过程中，分别给出了曼哈顿、欧拉以及契比雪夫 三种计算方式下，A * 算法的寻路过程，大家可以自己看看看其区别。
动画地址：https://kamacoder.com/tools/knight.html
计算出来 F 之后，按照 F 的 大小，来选去出队列的节点。
可以使用 优先级队列 帮我们排好序，每次出队列，就是F最小的节点。
实现代码如下：（启发式函数 采用 欧拉距离计算方式）

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 定义一个结构体，表示棋盘上骑士的位置和相关的 A* 算法参数
typedef struct {
    int x, y; // 骑士在棋盘上的坐标
    int g;    // 从起点到当前节点的实际消耗
    int h;    // 从当前节点到目标节点的估计消耗（启发式函数值）
    int f;    // 总的估计消耗（f = g + h）
} Knight;
#define MAX_HEAP_SIZE 2000000 // 假设优先队列的最大容量
// 定义一个优先队列，使用最小堆来实现 A* 算法中的 Open 列表
typedef struct {
    Knight data[MAX_HEAP_SIZE];
    int size;
} PriorityQueue;
// 初始化优先队列
void initQueue(PriorityQueue *pq) {
    pq->size = 0;
}
// 将骑士节点插入优先队列
void push(PriorityQueue *pq, Knight k) {
    if (pq->size >= MAX_HEAP_SIZE) {
        // 堆已满，无法插入新节点
        return;
    }
    int i = pq->size++;
    pq->data[i] = k;
    // 上滤操作，维护最小堆的性质，使得 f 值最小的节点在堆顶
    while (i > 0) {
        int parent = (i - 1) / 2;
        if (pq->data[parent].f <= pq->data[i].f) {
            break;
        }
        // 交换父节点和当前节点
        Knight temp = pq->data[parent];
        pq->data[parent] = pq->data[i];
        pq->data[i] = temp;
        i = parent;
    }
}
// 从优先队列中弹出 f 值最小的骑士节点
Knight pop(PriorityQueue *pq) {
    Knight min = pq->data[0];
    pq->size--;
    pq->data[0] = pq->data[pq->size];
    // 下滤操作，维护最小堆的性质
    int i = 0;
    while (1) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int smallest = i;
        if (left < pq->size && pq->data[left].f < pq->data[smallest].f) {
            smallest = left;
        }
        if (right < pq->size && pq->data[right].f < pq->data[smallest].f) {
            smallest = right;
        }
        if (smallest == i) {
            break;
        }
        // 交换当前节点与最小子节点
        Knight temp = pq->data[smallest];
        pq->data[smallest] = pq->data[i];
        pq->data[i] = temp;
        i = smallest;
    }
    return min;
}
// 判断优先队列是否为空
int isEmpty(PriorityQueue *pq) {
    return pq->size == 0;
}
// 启发式函数：计算从当前位置到目标位置的欧几里得距离的平方（避免开方，提高效率）
int heuristic(int x, int y, int goal_x, int goal_y) {
    int dx = x - goal_x;
    int dy = y - goal_y;
    return dx * dx + dy * dy; // 欧几里得距离的平方
}
// 用于记录从起点到棋盘上每个位置的最小移动次数
int moves[1001][1001];
// 骑士在棋盘上的8个可能移动方向
int dir[8][2] = {
    {-2, -1}, {-2, 1}, {-1, 2}, {1, 2},
    {2, 1}, {2, -1}, {1, -2}, {-1, -2}
};
// 使用 A* 算法寻找从起点到目标点的最短路径
int astar(int start_x, int start_y, int goal_x, int goal_y) {
    PriorityQueue pq;
    initQueue(&pq);
    // 初始化 moves 数组，-1 表示未访问过的位置
    memset(moves, -1, sizeof(moves));
    moves[start_x][start_y] = 0; // 起点位置的移动次数为 0
    // 初始化起始节点
    Knight start;
    start.x = start_x;
    start.y = start_y;
    start.g = 0; 
    start.h = heuristic(start_x, start_y, goal_x, goal_y);
    start.f = start.g + start.h; // 总的估计消耗
    push(&pq, start); // 将起始节点加入优先队列
    while (!isEmpty(&pq)) {
        Knight current = pop(&pq); // 取出 f 值最小的节点
        // 如果已经到达目标位置，返回所需的最小移动次数
        if (current.x == goal_x && current.y == goal_y) {
            return moves[current.x][current.y];
        }
        // 遍历当前节点的所有可能移动方向
        for (int i = 0; i < 8; i++) {
            int nx = current.x + dir[i][0];
            int ny = current.y + dir[i][1];
            // 检查新位置是否在棋盘范围内且未被访问过
            if (nx >= 1 && nx <= 1000 && ny >= 1 && ny <= 1000 && moves[nx][ny] == -1) {
                moves[nx][ny] = moves[current.x][current.y] + 1; // 更新移动次数
                // 创建新节点，表示骑士移动到的新位置
                Knight neighbor;
                neighbor.x = nx;
                neighbor.y = ny;
                neighbor.g = current.g + 5; // 每次移动的消耗为 5（骑士移动的距离平方）
                neighbor.h = heuristic(nx, ny, goal_x, goal_y);
                neighbor.f = neighbor.g + neighbor.h;
                push(&pq, neighbor); // 将新节点加入优先队列
            }
        }
    }
    return -1; // 如果无法到达目标位置，返回 -1
}
int main() {
    int n; 
    scanf("%d", &n);
    while (n--) {
        int a1, a2, b1, b2; // 起点和目标点的坐标
        scanf("%d %d %d %d", &a1, &a2, &b1, &b2);

        int result = astar(a1, a2, b1, b2); // 使用 A* 算法计算最短路径
        printf("%d\n", result); // 输出最小移动次数
    }
    return 0;
}

127. 骑士的攻击

一个坐标可以从 -infinity 延伸到 +infinity 的 无限大的 棋盘上，你的 骑士 驻扎在坐标为 [0, 0] 的方格里。
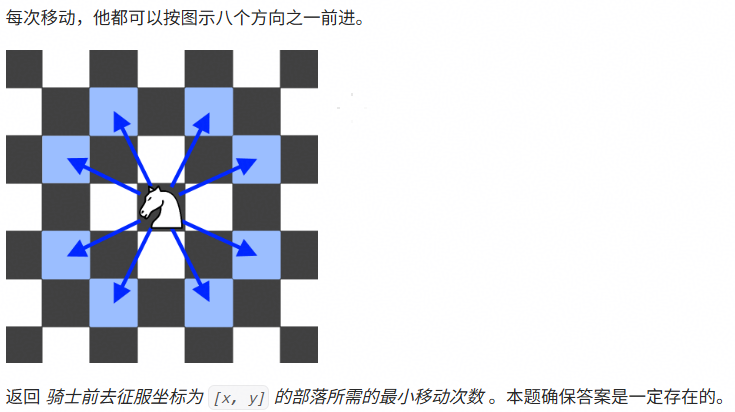
骑士的走法和中国象棋中的马相似，走 “日” 字：即先向左（或右）走 1 格，再向上（或下）走 2 格；或先向左（或右）走 2 格，再向上（或下）走 1 格。

每次移动，他都可以按图示八个方向之一前进。

示例 1：
输入：x = 2, y = 1
输出：1
解释：[0, 0] → [2, 1]
示例 2：
输入：x = 5, y = 5
输出：4
解释：[0, 0] → [2, 1] → [4, 2] → [3, 4] → [5, 5]
提示：
-300 <= x, y <= 300
0 <= |x| + |y| <= 300

#define SIZE 607
// 八个方向的偏移量
int offsets[8][2] = {{1, 2}, {2, 1}, {2, -1}, {1, -2},
                     {-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}};
int minKnightMoves(int x, int y)
{
    // 初始化起始点
    int queue[SIZE * SIZE][2];
    int head = 0, tail = 0;
    bool visited[SIZE][SIZE] = {false};
    int steps = 0;
    queue[tail][0] = 302; // 使用中心化偏移, -300 <= x, y <= 300 不让数组出现负数
    queue[tail][1] = 302;
    tail++;
    visited[302][302] = 0;
    while (head < tail) {
        int currLevelSize = tail - head;
        // 遍历当前层
        for (int i = 0; i < currLevelSize; i++) {
            int currX = queue[head][0];
            int currY = queue[head][1];
            head++;
            if ((currX == x + 302) && (currY == y + 302)) {
                return steps;
            }
            for (int j = 0; j < 8; j++) {
                int nextX = currX + offsets[j][0];
                int nextY = currY + offsets[j][1];
                if (visited[nextX][nextY] == 0) {
                    visited[nextX][nextY] = 1;
                    queue[tail][0] = nextX; // 使用中心化偏移
                    queue[tail][1] = nextY;
                    tail++;
                }
            }
        }
        steps++;
    }
    return steps;
}

拓扑排序指的是一种 解决问题的大体思路， 而具体算法，可能是广搜也可能是深搜。
大家可能发现 各式各样的解法，纠结哪个是拓扑排序？
其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。
实现拓扑排序的算法有两种：卡恩算法（BFS）和DFS
一般来说我们只需要掌握 BFS （广度优先搜索）就可以了，清晰易懂，如果还想多了解一些，可以再去学一下 DFS 的思路，但 DFS 不是本篇重点。

207. 课程表_拓扑排序

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

bool canFinish(int numCourses, int **prerequisites, int prerequisitesSize, int *prerequisitesColSize)
{
    int **edges = (int **)malloc(sizeof(int *) * (numCourses)); // 邻接表
    int *edgeColSize = (int *)malloc(sizeof(int) * (numCourses));
    memset(edgeColSize, 0, sizeof(int) * (numCourses));
    for (int i = 0; i < (numCourses); i++) {
        edges[i] = (int *)malloc(sizeof(int) * 2000);
    }
    int indeg[numCourses]; // 存储每个节点的入度
    memset(indeg, 0, sizeof(indeg));
    for (int i = 0; i < prerequisitesSize; ++i) {
        int a = prerequisites[i][1]; // 依赖项，学习b之前需要学习a b->a
        int b = prerequisites[i][0];
        edgeColSize[a]++;
        edges[a][edgeColSize[a] - 1] = b;
        ++indeg[b];
    }
    int queue[numCourses];
    int head = 0, tail = 0;
    // 1. 入度为0，进队列，示例即为 课程3与课程4，因为他们没有依赖
    for (int i = 0; i < numCourses; ++i) {
        if (indeg[i] == 0) {
            queue[tail++] = i;
        }
    }
    int visited = 0;
    // 2. BFS，找到入度为0的节点，然后出队列，更新入度，继续找入度为0的节点
    while (head < tail) {
        ++visited;
        int u = queue[head++];
        for (int i = 0; i < edgeColSize[u]; ++i) {
            --indeg[edges[u][i]]; // 每次入度减一
            if (indeg[edges[u][i]] == 0) {
                queue[tail++] = edges[u][i];
            }
        }
    }
    for (int i = 0; i < numCourses; i++) {
        free(edges[i]);
    }
    free(edges);
    return visited == numCourses;
}
int main()
{
    // 提供了图的邻接表表示
    int a[] = {0,1};
    int b[] = {0,2};
    int c[] = {1,3};
    int d[] = {2,4};
    int *prerequisites[] = {a,b,c,d};
    int prerequisitesSize = 4; // 有多少条约束关系
    int numCourses = 5; // 有多少个节点
    int prerequisitesColSize;
    bool ret = canFinish(numCourses, prerequisites, prerequisitesSize, &prerequisitesColSize);
    return 0;
}

279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

#include <stdio.h>
#include <string.h>
#include <stdlib.h> 
// 队列 && BFS
struct Link
{
    int data;
    struct Link* next;
};
struct Queue
{
    struct Link *front; // 队头删除
    struct Link *rear;  // 队尾新增
    int size;
};
void QueueInit(struct Queue *queue)
{
    queue->front = NULL;
    queue->rear  = NULL;
    queue->size  = 0;
}
int QueueEmpty(struct Queue *queue)
{
    return (queue->size == 0);
}
void QueuePush(struct Queue *queue, const int data)
{
    struct Link *node;
    node = (struct Link *)malloc(sizeof(struct Link));
    
    node->data = data;
    node->next = NULL;
	printf("push queue %d\n", data);
    
    if (QueueEmpty(queue)) {
        queue->front = node;
        queue->rear = node;
    } else {            
        queue->rear->next = node; // 往队尾增加一个元素
        queue->rear = node;       // 设置当前元素为队尾
    }
    ++queue->size;
}
int QueuePop(struct Queue *queue, int *data)
{
    if (QueueEmpty(queue)) {
            return 0;
    }
    struct Link *tmp = queue->front; // 队列头删除节点
    *data = queue->front->data;
    queue->front = queue->front->next;
	printf("pop queue %d\n", *data);
    free(tmp);
    --queue->size;
    return 1;
}
void QueueDestroy(struct Queue* queue)
{
     struct Link *tmp;
     while(queue->front) { 
         tmp = queue->front;
         queue->front = queue->front->next;
         free(tmp);
     }
}
#define LENGTH 10000
int numSquares(int n) {
	int i, j,next = 0, curr = 0, size = 0, steps = 0, *visited;
	int *data = NULL;
    struct Queue *queue = NULL;
	queue = (struct Queue *)malloc(sizeof(struct Queue)); // 为根节点分配空间
	if (n == 0 || n == 1) {
		return n;
	}
	QueueInit(queue);
	visited = (int *)malloc(sizeof(int) * (LENGTH+1));
	data    = (int *)malloc(sizeof(int));
	memset(visited, 0, sizeof(int)*(LENGTH+1));

	QueuePush(queue, 0); // 根节点入队列，入队为队尾
	visited[0] = 1;      // 访问标记
	// 顺序遍历每一行，所以当节点差出现 0 时，此时一定是最短的路径
	while (!QueueEmpty(queue)) 
	{
		steps++; 
		size = queue->size;
		printf("------------steps is %d------------\n", steps);
		for (i = 0; i < size; i++) {
			QueuePop(queue, data);  // 队首元素出队
			curr = *data;           // 队首元素值
			printf("------curr is %d------\n", curr);
			for(j = 1; j*j <= n; j++) {
				next = curr+j*j; 
				printf("next is %d\n", next);
				if (next == n) {
					printf("!! bingo !! next == %d\n", n);
					return steps;
				} if (next > n) {
					break;
				} if (visited[next]) {
					continue;
				}
				visited[next] = 1;
				QueuePush(queue, next); // 节点入队
			}
		}
	}
	QueueDestroy(queue);
	return steps;
}

int main() {
	printf("\nresult is %d\n",numSquares(10));
	return 0;
}

解题思路::求解 10 的完全平方数为例，利用图的BFS遍历（之前我们学习过BFS是利用队列），即按层次进行遍历，遍历值不超过 n 的平方根（j*j < n），如下图所示，所以依次进队列的是 0，然后0出队列，进 1->4->9，出队列1，然后入队 2->5->10，10 满足题意退出（图中多画了10 右面的情况是为了说明，如果出现之前出现过的值，则直接返回结果，这一小技巧，避免BFS遍历已访问的元素，如下图中黑色的点）

如果借助打印，结果将如下所示：

797. 所有可能的路径

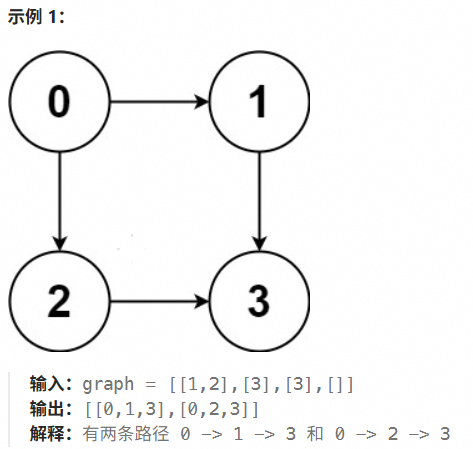
给你一个有 n 个节点的 有向无环图（DAG），请你找出从节点 0 到节点 n-1 的所有路径并输出（不要求按特定顺序）
graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

int **ans;
int stack[15]; // 存储路径
int top;
void dfs(int x, int n, int **graph, int *graphColSize, int *returnSize, int **returnColumnSizes)
{
    if (x == n) {
        int *tmp = (int *)malloc(sizeof(int) * top);
        memcpy(tmp, stack, sizeof(int) * top);
        ans[*returnSize] = tmp;
        (*returnColumnSizes)[(*returnSize)++] = top;
        return;
    }
    // 邻接表表示的元素
    for (int i = 0; i < graphColSize[x]; i++) {
        int nextNode = graph[x][i];
        stack[top++] = nextNode;
        dfs(nextNode, n, graph, graphColSize, returnSize, returnColumnSizes);
        top--;
    }
}
int **allPathsSourceTarget(int **graph, int graphSize, int *graphColSize, int *returnSize, int **returnColumnSizes)
{
    top = 0;
    stack[top++] = 0;
    ans = (int **)malloc(sizeof(int *) * pow(2,15));
    *returnSize = 0;
    *returnColumnSizes = malloc(sizeof(int) * pow(2,15));
    dfs(0, graphSize - 1, graph, graphColSize, returnSize, returnColumnSizes);
    return ans;
}
int main()
{
    // 提供了图的邻接表表示
    int a[] = {1,2};
    int b[] = {3,};
    int c[] = {3};
    int d[] = {};
    int *graph[] = {a,b,c,d};
    int returnSize = 0;
    int **returnColumnSizes = (int **)malloc(sizeof(int *) * pow(2,15));
    int graphColSize[] = {2,1,1,0};
    int graphSize = sizeof(graph) / sizeof(graph[0]);
    int **res = allPathsSourceTarget(graph, graphSize, graphColSize, &returnSize,returnColumnSizes);
    for(int i = 0; i < returnSize; i++){
        for(int j = 0; j < (*returnColumnSizes)[i]; j++){
            printf("%5d", res[i][j]);
        }
        printf("\n");
    }
    return 0;
}