1.14 LeetCode总结（基本算法）_二分查找类

原创已于 2025-10-05 18:39:04 修改 · 500 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #职场和发展

于 2020-05-05 20:34:46 首次发布

日刻一诗专栏收录该内容

30 篇文章

订阅专栏

本文深入解析二分查找算法，涵盖基本实现、搜索插入位置、寻找第一个错误版本等核心问题，提供高效代码示例与优化策略。

编程总结

每每刷完一道题后，其思想和精妙之处没有地方记录，本篇博客用以记录刷题过程中的遇到的算法和技巧

二分查找模板

// (版本一) 左闭右闭区间 [left, right]
int search(int *nums, int numsSize, int target)
{
    int left   = 0;
    int right  = numsSize - 1;
    int middle = 0;
    //若left小于等于right，说明区间中元素不为0
    while (left <= right) {
        //更新查找下标middle的值
        middle = left + (right - left) / 2;
        //此时target可能会在[left,middle-1]区间中
        if (nums[middle] > target) {
            right = middle - 1;
        }
        //此时target可能会在[middle+1,right]区间中
        else if (nums[middle] < target) {
            left = middle + 1;
        }
        //当前下标元素等于target值时，返回middle
        else if (nums[middle] == target) {
            return middle;
        }
    }
    //若未找到target元素，返回-1
    return -1;
}

// (版本二) 左闭右开区间 [left, right)
int search(int *nums, int numsSize, int target) 
{
    int length = numsSize;
    int left = 0;
    int right = length;	//定义target在左闭右开的区间里，即：[left, right)
    int middle = 0;
    while (left < right) {  // left == right时，区间[left, right)属于空集，所以用 < 避免该情况
        int middle = left + (right - left) / 2;
        if (nums[middle] < target) {
            //target位于(middle , right) 中为保证集合区间的左闭右开性，可等价为[middle + 1,right)
            left = middle + 1;
        } else if (nums[middle] > target){
            //target位于[left, middle)中
            right = middle ;
        } else {	// nums[middle] == target ，找到目标值target
            return middle;
        }
    }
    //未找到目标值，返回-1
    return -1;
}

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 为无重复元素的升序排列数组
-10^4 <= target <= 10^4

思路：区间是左闭右闭，套用模板一

手法1：返回的是将被按顺序插入的位置（即最后的Left位置）

int searchInsert(int *nums, int numsSize, int target)
{
    int left   = 0;
    int right  = numsSize - 1;
    int middle = 0;
    //若left小于等于right，说明区间中元素不为0
    while (left <= right) {
        //更新查找下标middle的值
        middle = left + (right - left) / 2;
        //此时target可能会在[left,middle-1]区间中
        if (nums[middle] > target) {
            right = middle - 1;
        }
        //此时target可能会在[middle+1,right]区间中
        else if (nums[middle] < target) {
            left = middle + 1;
        }
        //当前下标元素等于target值时，返回middle
        else if (nums[middle] == target) {
            return middle;
        }
    }
    // 返回它将会被顺序插入的位置
    return left;
}

278. 第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数
示例 1：
输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。
示例 2：
输入：n = 1, bad = 1
输出：1
提示：
1 <= bad <= n <= 2^31 - 1

思路是先找到第一个出错的版本，即 isBadVersion == true. 然后找它的下一个 false 即为所求。，但效率有点低，特别对于第一次如果找到的 true 比较靠前，将多走很多步才能找到下一个 false 的下标。

int firstBadVersion(int n)
{
    int left   = 1; // 按照题意等于1
    int right  = n; // 按照题意可以等于n
    int middle = 0;
    // 若left小于等于right，说明区间中元素不为0
    while (left <= right) {
        // 更新查找下标middle的值
        middle = left + (right - left) / 2; // 这里不能用 middle = (left + right) / 2; 会overflow
        // printf("%d %d", left, right);
        if (isBadVersion(middle) == true) { // 此时target可能会在[left,middle-1]区间中
            right = middle - 1;
        }
        else if (isBadVersion(middle) == false) { // 此时target可能会在[middle+1,right]区间中
            left = middle + 1;
        }
    }
    return left;
}

手法1：这里不能用 middle = (left + right) / 2; 会overflow

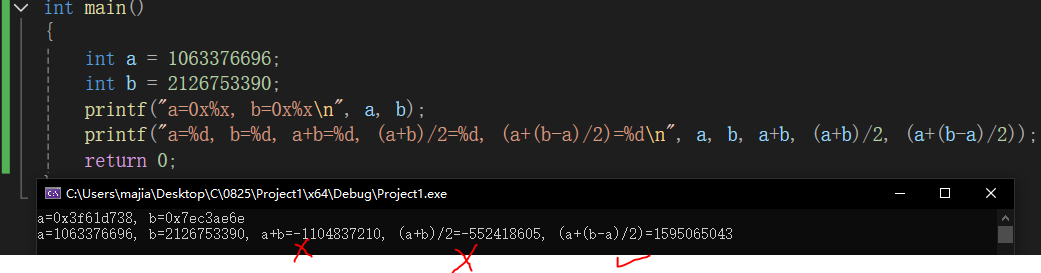
在这里插入图片描述

a 与 b 本身都是有效的32bit 十进制数，两者直接相加有可能会Overflow(原因如上图所示)

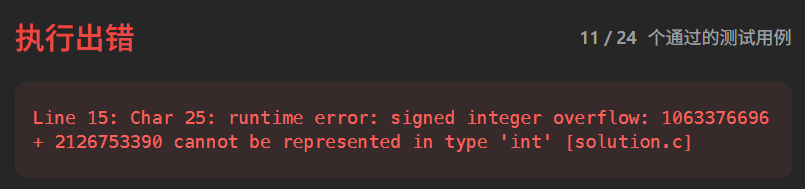
在这里插入图片描述

2389. 和有限的最长子序列

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。
返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中元素之和小于等于 queries[i] 的子序列的最大长度。
子序列是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：
输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：

子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。
示例 2：
输入：nums = [2,3,4,5], queries = [1]
输出：[0]
解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 。
提示：
n == nums.length
m == queries.length
1 <= n, m <= 1000
1 <= nums[i], queries[i] <= 10^6

思路：根据题意返回 left 或 right

上一道是返回 left，本题是返回 right
// left是最后一个大于等于 target的偏移
// right是最后一个小于等于 target的偏移

static int Cmp(const void* a, const void* b)
{
    int* aa = (int*)a;
    int* bb = (int*)b;
    return *aa - *bb;
}
int search(int *nums, int numsSize, int target)
{
    int left = 0;
    int right = numsSize;
    int middle = 0;
    //若left小于等于right，说明区间中元素不为0
    while (left <= right) {
        middle = left + (right - left) / 2;
        //此时target可能会在[left,middle-1]区间中
        if (nums[middle] > target) {
            right = middle - 1; // right是最后一个小于等于 target的偏移
        }
        //此时target可能会在[middle+1,right]区间中
        else if (nums[middle] < target) {
            left = middle + 1; // left是最后一个大于等于 target的偏移
        }
        //当前下标元素等于target值时，返回middle
        else if (nums[middle] == target) {
            return middle; // left与right相同
        }
    }
    return right; // right是最后一个小于等于 target的偏移
}
// [0, 1, 3, 7, 12] -- 前缀和
// [3, 10, 21]
int *answerQueries(int *nums, int numsSize, int *queries, int queriesSize, int *returnSize)
{
    qsort(nums, numsSize, sizeof(int), Cmp);
    int* f = (int*)malloc(sizeof(int) * (numsSize + 1));
    f[0] = 0;
    memset(f, 0, sizeof(int) * (numsSize + 1));
    for (int i = 0; i < numsSize; i++) { // 前缀和 f[i] 表示的是前i个元素 不包括num[i]
        f[i + 1] = f[i] + nums[i];
    }
    int *answer = (int *)malloc(sizeof(int) * queriesSize);
    for (int i = 0; i < queriesSize; i++) {
        answer[i] = search(f, numsSize, queries[i]); // 二分前缀
    }
    *returnSize = queriesSize;
    return answer;
}
int main()
{
    int nums[4] = { 4, 5, 2, 1 };
    int queries[3] = { 3, 10, 21 };
    int returnSize = 0;
    int* ret = answerQueries(nums, 4, queries, 3, &returnSize);
    for (int i = 0; i < returnSize; i++) {
        printf("%d ", ret[i]);
    }
    return 0;
}

875. 爱吃香蕉的珂珂

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：
输入：piles = [3,6,7,11], h = 8
输出：4
示例 2：
输入：piles = [30,11,23,4,20], h = 5
输出：30
示例 3：
输入：piles = [30,11,23,4,20], h = 6
输出：23

提示：
1 <= piles.length <= 10^4
piles.length <= h <= 10^9
1 <= piles[i] <= 10^9

// 以speed的速度, 能否在H小时吃完
bool canFinish(int *piles, int pilesSize, int speed, int h)
{
    long sum = 0;
    for (int i = 0; i < pilesSize; i++) {
        sum += (piles[i] + speed - 1) / speed; /* 向上取整 */
    }
    if (h >= sum) {
        return true;
    } else {
        return false;
    }
}
int minEatingSpeed(int *piles, int pilesSize, int h)
{
    int left = 1;
    int right= 1;
    int middle = 0;
    // 求右边界
    for (int i = 0; i < pilesSize; i++) {
        right = fmax(right, piles[i]);
    }
    // 二分查找左边边界模板 
    while (left <= right) {
        middle = left + (right - left) / 2; // middle为速度
        if (canFinish(piles, pilesSize, middle, h) == true) {
            right = middle - 1; // 满足，就减速，把right改小
        }
        else if (canFinish(piles, pilesSize, middle, h) == false) {
            left = middle + 1; // 不满足，就要提速，提速就是改left变量
        }
        else {
            printf("ERROR\n");
        }
    }
    return left;
}
int main()
{
    int piles[5] = { 30,11,23,4,20 };
    int h = 6;
    int ret = minEatingSpeed(piles, 5, h);
    printf("%d ", ret);
    return 0;
}