这篇博客探讨了区间（Interval）问题在编程中的应用，包括合并相交区间、插入新区间以及确定最少会议室数量等。文章引用了LeetCode和LintCode上的题目，并提供了通用模板和解题思路，强调了区间排序的重要性以及处理重叠和插入问题的策略。通过实例和代码演示了解决这类问题的方法。
该博文参考了如下blog：
https://emre.me/coding-patterns/merge-intervals/
Interval中文意思是间隔，可以理解为区间。生活中很多可以描述为interval，例如会议时间的区间，公交车运行站点区间等等。一般理解为时间区间较好，多数题目都可以按照时间区间理解，有助于我们了解题目的具体场景。
给定两个间隔A和B，会有6种不同的方式这两个间隔之间的关系:
但是如果a.start <= b.start，也就是给定的区间是起始时间有序排列，那么只有1，2，3种情况，其中2和3是overlap(交叉的)。如果我们要merge 交叉的a和b两个区间，则对应的结果c如图：
给出公式就是:
c.start = a.start
// c的开始取a的start，也就是min(a.start, b.start)，因为a，b有序，所以即为a.start
c.end = max(a.end, b.end)
// c的结束时间取a和b的结束时间的最晚值
如果我们要判断两个interval是否交叉，如上图所示，则只需要判断b的开始时间是否大于a的结束时间(b.start > a.end)，显然如果大于就不会相交，而小于必然相交。等于是否表示相交需要看题目的规定。
给出了一个解决interval相关问题的模板:
public boolean genericIntervalTemplate(int[][] intervals) {
if (intervals.length == 0) //合法性检查，一般需要check intervals是否为空（*根据实际情况返回对应的结果）
return $result;
Arrays.sort(intervals, (a, b) -> a[0] - b[0]); // 根据起始时间排序，这是解决interval问题的关键，时间复杂度为O(nlogn)
int[] prev = intervals[0]; // 保存一个prev指针保存上一次的结果，默认情况下赋值为第一个interval
for (int i = 1; i < intervals.length; i++) { // 从1开始，检查intervals集合中剩下的interval
int[] current = intervals[i]; // 要处理的当前interval curr
if (doIntervalsOverlap(prev, current)) { // 如果存在交叉，则做处理（*根据实际情况返回对应的结果）
// if overlap Do business logic
}
prev = current; // 将prev指针保存的结果更新为当前的interval （*根据实际情况返回对应的结果）
}
return $result; // 返回结果（*根据实际情况返回对应的结果）
}
private boolean doIntervalsOverlap(int[] i1, int[] i2) {
//if the start of the second interval is greater or equal than the end of the first interval they dont overlap
// > or >= depends on the exact problem
// for example in some cases [4,6] [6,10] are considered overlapping, in some not
if (i2[0] >= i1[1])
return false;
return true;
}
注意三点:
- Intervals一定要排序；
- Interval的边缘，例如 [4,6] [6,10] 是否算overlap需要按照题目规定；
- 如果有排序，则时间复杂度为O(nlogn)，已经排好序的intervals处理只有O(n)。
下面直接看具体的题目:
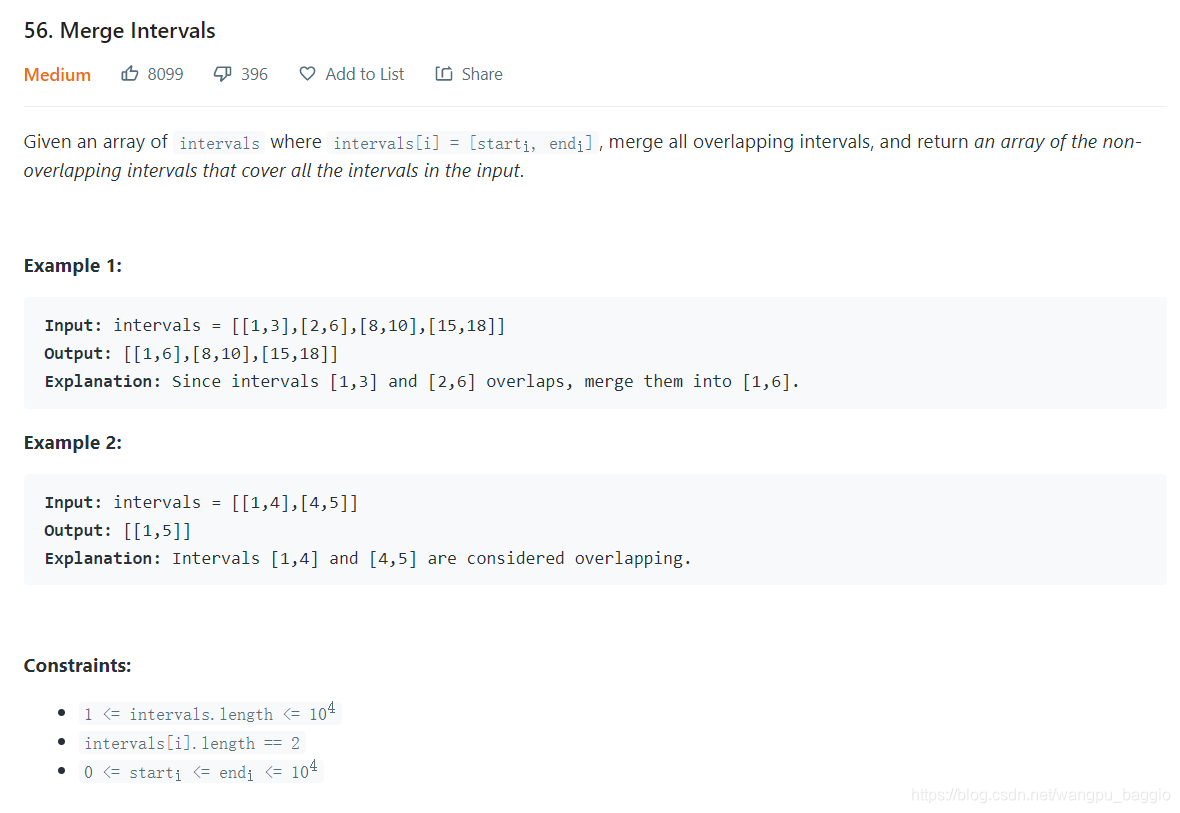
https://leetcode.com/problems/merge-intervals/
这道题就是merge 有overlap的interval，直接套用模板（该题为之前完成，和模板有一点差距，但是思想完全一致）:
public int[][] merge(int[][] intervals) {
// 返回值
LinkedList<int[]> res = new LinkedList<>();
// 题目没有说数组有序，所以需要排序
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
// merge之后的c :
// c.start = a.start
// c.end = max(a.end, b.end)
// 先将第一个子数组加到res中，保留该子数组作为后面动态变化的参考
// 上一个结果的end小于当前子数组的start，不存在交叉，直接add到结果中
// 否则(上一个结果的end大于或者等于当前子数组的start，存在交叉，此时只需要修改end值)
int[] newInterval = intervals[0];
res.add(newInterval);
for (int[] curr : intervals) {
// 存在交叉
if (curr[0] <= newInterval[1]) {
newInterval[1] = Math.max(curr[1], newInterval[1]);
} else {
newInterval = curr;
res.add(newInterval);
}
}
// 第一个参数可以传递res.size，但是传0也是可以的，实现中会替换成res.size
return res.toArray(new int[0][]);
}
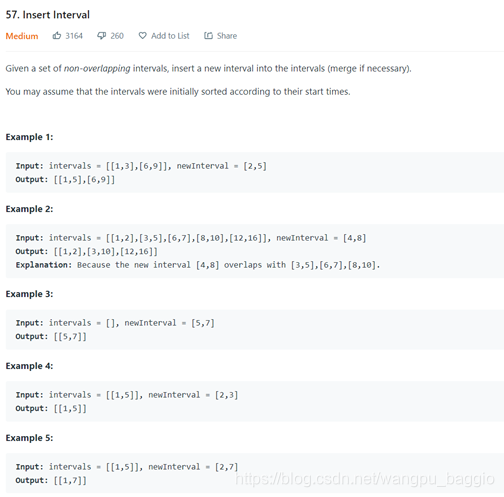
https://leetcode.com/problems/insert-interval/
这道题和之前的题目不同，因为是需要插入interval，所以我们换一种思路。
将给的intervals理解为已经预定好的会议，这样定义一个全局指针i，从左到右去查看怎么插入一个新的会议。
如果新会议的开始时间比预定好的会议要晚，则这些会议都可以保留在结果中；
直到找到新会议的开始时间早于预定好的会议的结束时间，存在overlap。注意此时循环条件是只要存在会议的开始时间小于等于新会议的结束时间，都进入循环，进行会议时间的merge。
最后将出循环的剩余没有关系的会议预定给加到结果中，示意图如下：
如果不好理解，则参考视频：https://www.youtube.com/watch?v=E9IYRG_WYcM
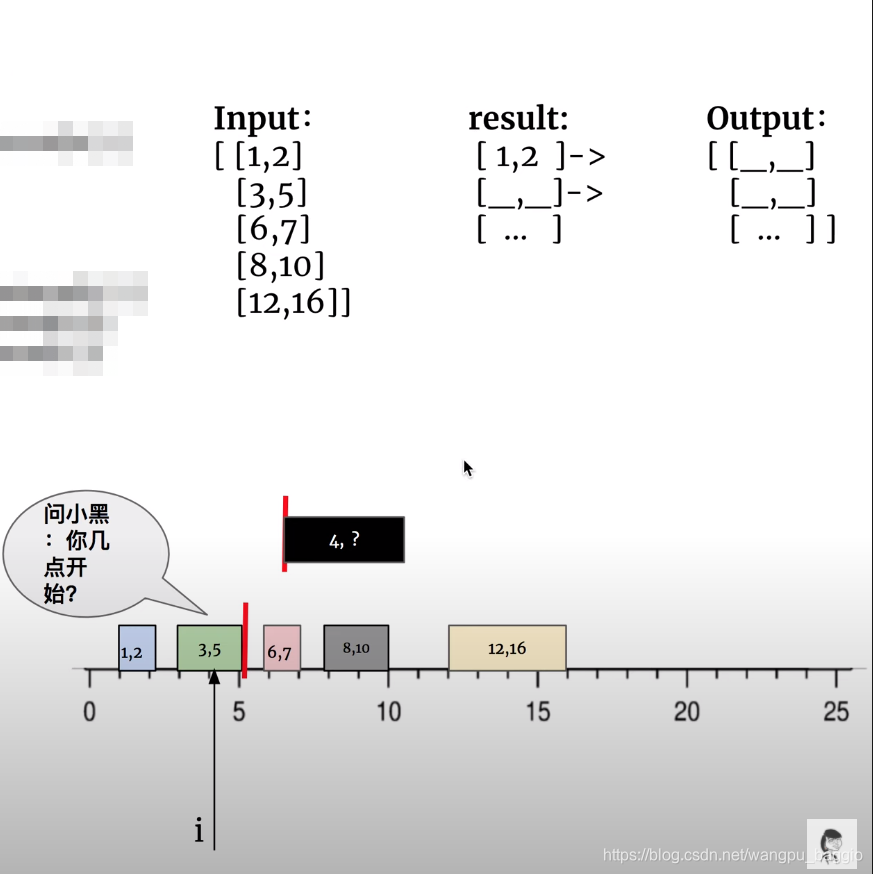
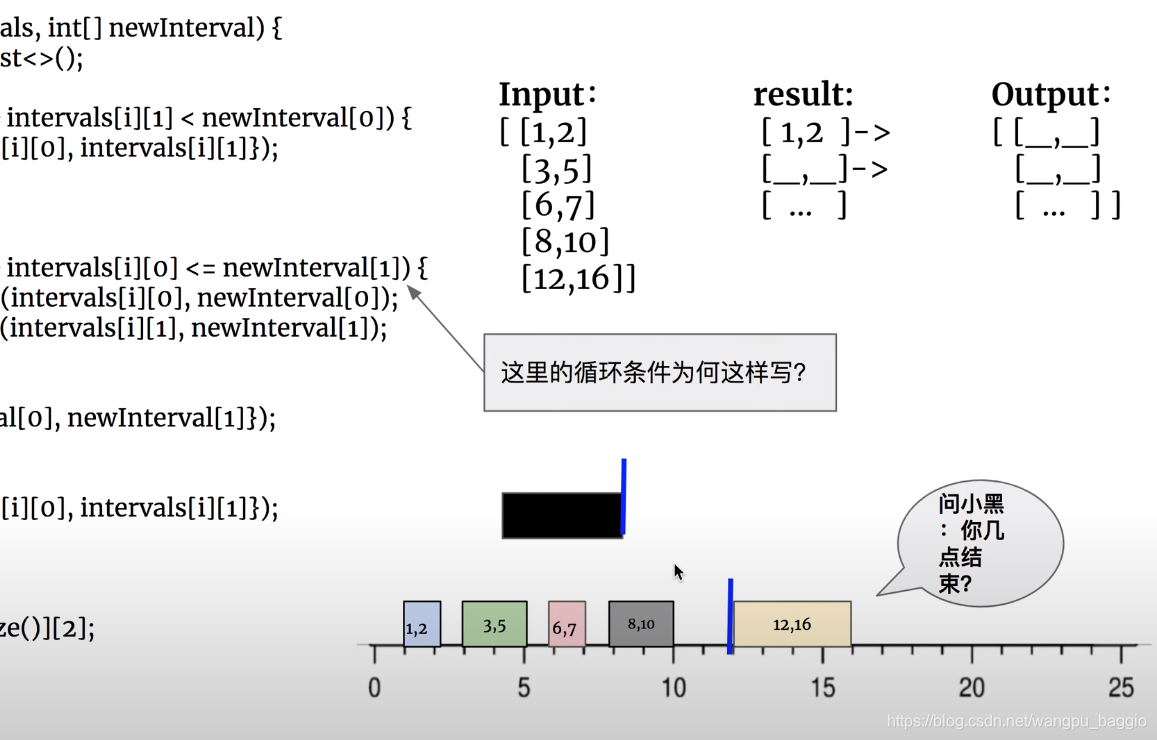
代码如下：
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> res = new ArrayList<>();
int i = 0; // 全局指针
// 将左侧和newInterval不相关的interval加到结果中去
while(i < intervals.length && newInterval[0] > intervals[i][1]) {
res.add(intervals[i]);
i++;
}
// newInterval的结束如果大于或者等于interval的开始，则会发生merge关系
// merge过程为左边界取左侧的最小值，右边界取最大值
while(i < intervals.length && newInterval[1] >= intervals[i][0]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
res.add(newInterval);
// 将没有关系的右侧intervals部分加到结果中
while(i < intervals.length) {
res.add(new int[]{intervals[i][0], intervals[i][1]});
i++;
}
return res.toArray(new int[0][]);
}
下面是两个meeting room的题，因为我没leetcode的会员，这个题就从lintcode中截图了，题目都是一样的:
https://www.lintcode.com/problem/920/description
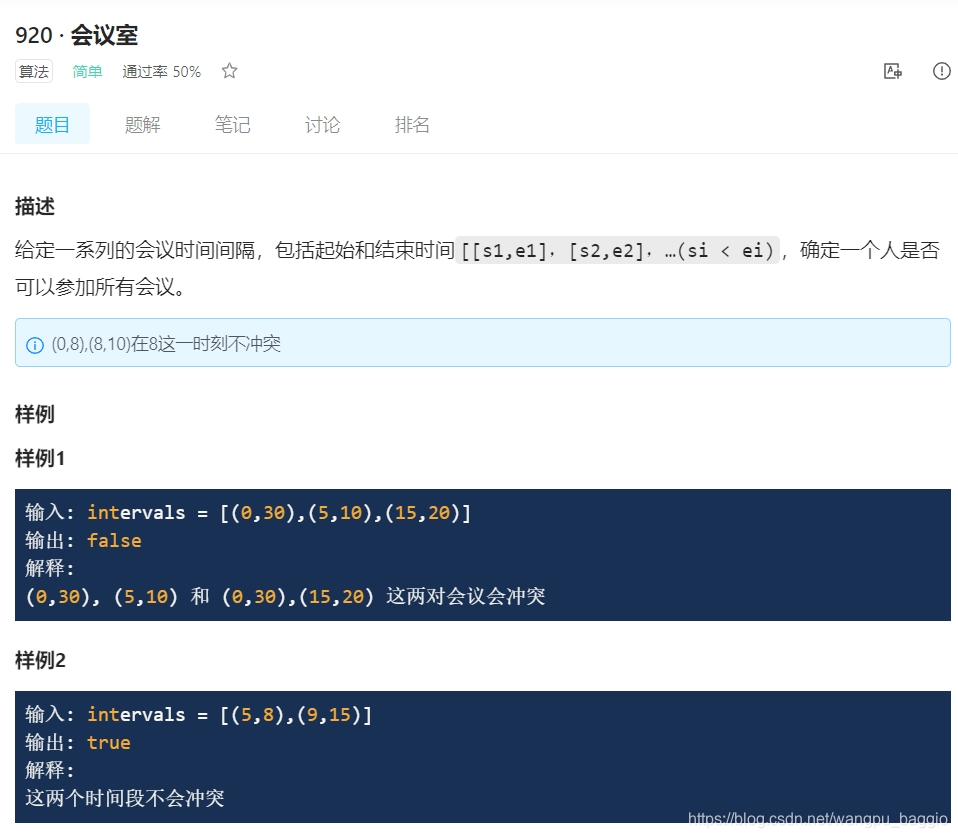
这个题很简单，而且只需要返回true或false，直接套用模板:
public boolean canAttendMeetings(List<Interval> intervals) {
if (intervals.isEmpty()) return true;
Collections.sort(intervals, (a, b) -> a.start - b.start);
Interval prev = intervals.get(0);
for (int i = 1; i < intervals.size(); i++) {
if (intervals.get(i).start < prev.end) {
return false;
}
prev = intervals.get(i);
}
return true;
}
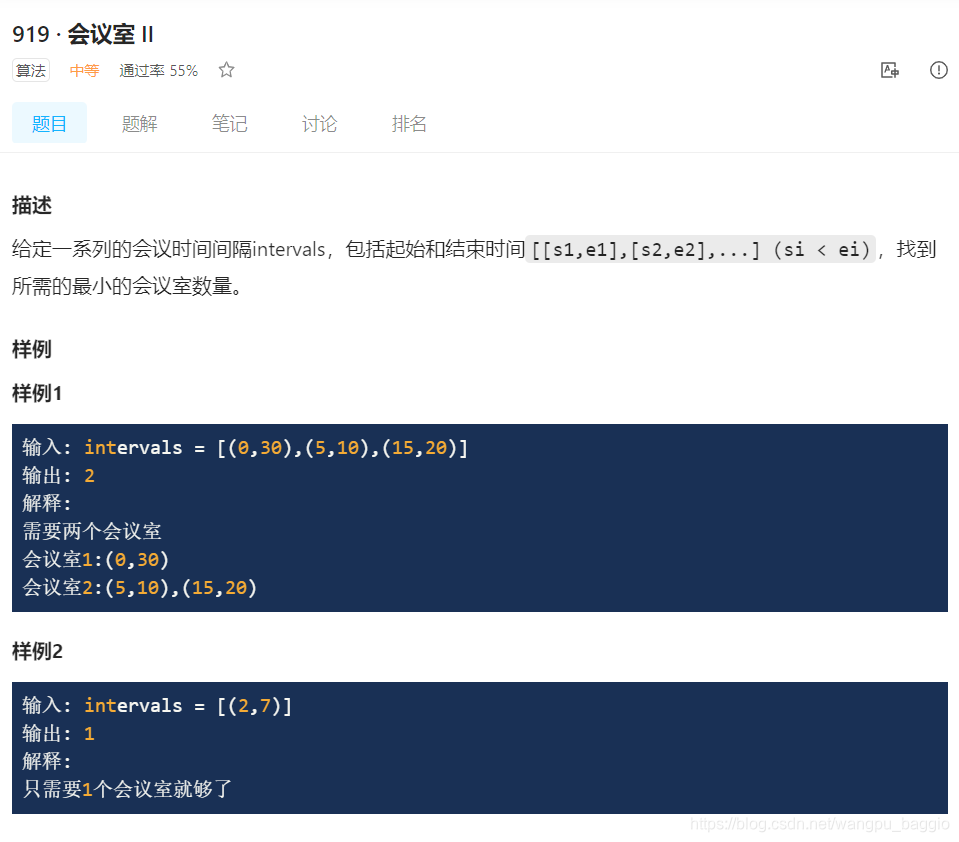
https://www.lintcode.com/problem/919/description
这个题，需要的最少meeting room的数量，和上面的题稍微有点不同。不同之处主要是如何放置当前会议的时间段，需要去找到过去已经放置好的时段里的最早结束时间，如果当前时段的开始时间晚于这个时间，就可以放到该会议时段的后面，也就是不需要新的会议室。所以需要存储以前所有的会议时段。考虑到每次需要出栈的是以前的最早结束的会议，所以采用小根堆存储，每次出栈的是按照最小的结束时间为标准。
放置图如下所示:
代码如下:
public int minMeetingRooms(List<Interval> intervals) {
if (intervals.isEmpty() || intervals.size() == 1) return intervals.size();
Collections.sort(intervals, (a, b) -> a.start - b.start);
// 小根堆，存储会议，出堆按照结束会议的最早时间
PriorityQueue<Interval> minHeap = new PriorityQueue<>((a, b) -> a.end - b.end);
minHeap.offer(intervals.get(0));
for (int i = 1; i < intervals.size(); i++) {
Interval prev = minHeap.poll();
Interval curr = intervals.get(i);
if (curr.start >= prev.end) {
// 没有交叉，可以分配到同一个时间，将end时间延长
prev.end = Math.max(prev.end, curr.end);
} else { // 交叉，offer当前的时间间隔
minHeap.offer(curr);
}
minHeap.offer(prev);
}
return minHeap.size();
}
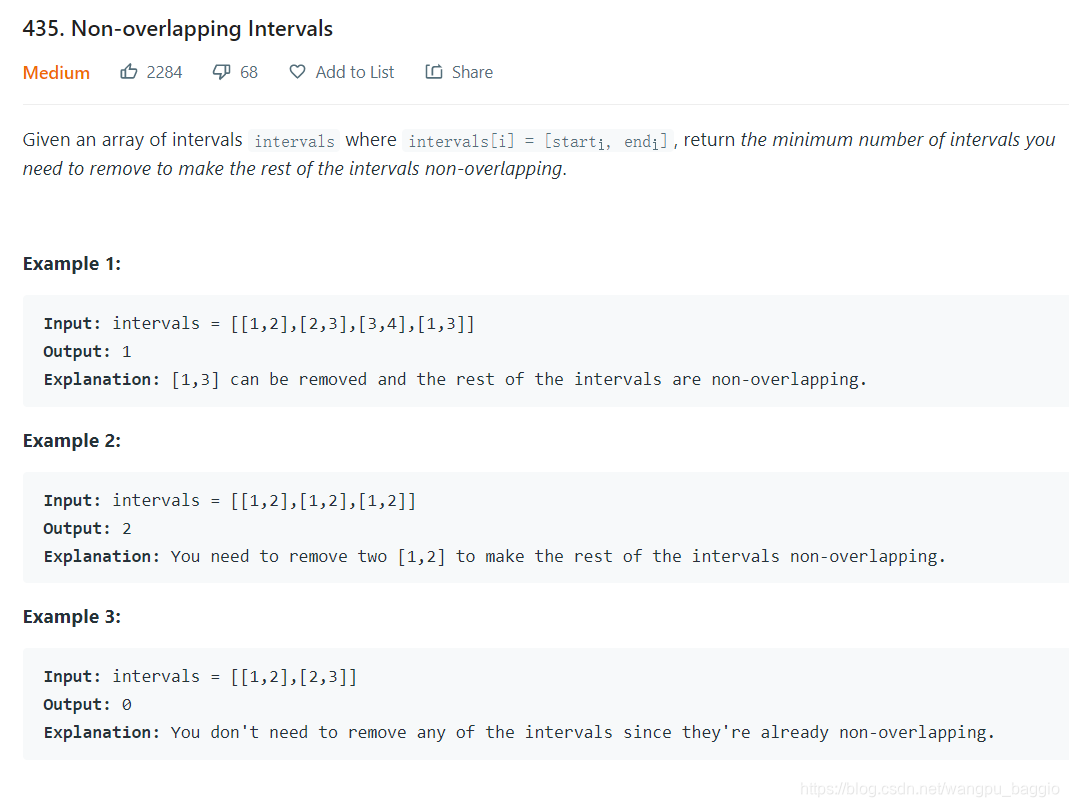
https://leetcode.com/problems/non-overlapping-intervals/
套用模板，很简单，注释在代码上已经标注了。
public int eraseOverlapIntervals(int[][] intervals) {
List<int[]> res = new ArrayList<>();
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
int[] prev = intervals[0];
int count = 0; // 移动出去的数量
for (int i = 1; i < intervals.length; i++) {
int[] curr = intervals[i];
if (curr[0] < prev[1]) { // 交叉，需要移出结束时间大的，保留较早时间结束的interval，count加1
prev[0] = curr[1];
prev[1] = Math.min(prev[1], curr[1]);
count++;
} else {
prev = curr;
}
}
return count;
}
扫一扫
到【灌水乐园】发言
