并查集Day2（基础~路径压缩带权并查集扩展域并查集）-优快云博客

本文链接：https://blog.youkuaiyun.com/wangluoyi1/article/details/144649709

带权并查集

导入：

有关并查集的基本操作是合并和查找，具体用递归来实现，带权并查集意味着在原先普通并查集每个集合的每条边 $or$ 每个点都有权值。会根据题目具体条件，根据情况去在原先的 $father$ 数组里加条件限定节点之间的联系，这一般情况下可分为维护 $dist$ (记录当前节点到根结点的距离)和维护 $size$ (集合内结点个数)的并查集。做提前预告，并且在之后的文中所提到的权值都指的是以上两种情况。

证明其正确性：

考虑带权并查集对初学者莫过于模糊，先可以用并查集Day1已经讨论过的知识来解释：

因为使用带权并查集要维护每一个结点到其祖先结点的权值( $dist$ )，之后还要维护每一个集合的大小( $num$ )。
所以为了在合并集合时更方便，只需在根结点的位置上存储该集合的大小，之后又由于我们在路径压缩的时候压缩权值，就只用 $O(1)$ 能查询每个点到其根结点的权值。

更详细的可参考OI-WIKI的证明

实现：

Part1:有关 $size$ 的带权并查集

int find(int x)
{
    if(father[x] == x) return x;   
    int fn = find(father[x]);     //递归找father[x]的根结点fn
    size[x] += size[father[x]];   //在回溯的时候加上原先根结点的的size
    return father[x] = fn;        //因为要找到祖先后size才能确定
}

尤其是递归这部分，为什么要在回溯时加 $size$ ？

由于在寻找祖先，原先的集合的祖先在新的集合中结点位置还没有固定，因此我们需要先找到当前 $x$ 结点的 $father[x]$ 更新后的位置，随后才能在回溯时一步步更新结点。
另外加一点，在更新就会有不同情况：看几道例题

例题一：信息传递

简单说当找到有一个方式能代替传递次数，可以假想如果我要传到距离这个集合中离自己这个节点距离为2的另一个结点，那么是不是就可以看作是结点个数呢。具体可以看注释里的例子和思路：

/*--------------------------------------------------------------------
思路
将人数作为边的权值
把接受信息的人作为父亲，发送信息的人作为儿子
当有两个集合有共同的祖先时证明传递成功

1 2  1->2->3->4->5
2 3  5->5
3 4  0+1+1 = 2
4 5 过程：5得知4   -->5得知5、4、3   
5 4       4得知5、3-->4得知4、3、2、1 

---------------------------------------------------------------------*/
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
namespace Dino
{
	const int N = 1e5+100;
	const int INF = 0x3f3f3f3f;
	int a[N], fa[N], num[N];
	int n, minn = INF;
	int find(int x)
	{
		if(fa[x] == x) return x;
		int fn = find(fa[x]);
		num[x] += num[fa[x]];
		return fa[x] = fn;
	}
	inline void check(int x,int y)
	{
		int fx = find(x);
		int fy = find(y);
		if(fx != fy)
		{
			fa[fx] = fy;
			num[x] = num[y]+1;
		}else{
			minn = min(minn,num[x]+num[y]+1);
		}
	}
	auto work=[]()
	{
		memset(a,0,sizeof(a));
		cin >> n;
		for(int i=1; i <= n; i++)
		{
			fa[i] = i;
		}
		for(int i=1,x; i <= n; i++)
		{
			cin >> x;
			check(i,x);
		}
		cout << minn << endl; 
	};
}
signed main()
{
	fastio;
	return Dino::work(), 0;
}

Part2:有关 $dist$ 的带权并查集

不难，可以先了解一个概念向量。既然向量既有大小又有方向刚好与我们的带权并查集匹配，那不就爽了。另外，因为 $Union$ 函数之所以不存在是因为其他操作中完全可以取而代之。

例题一：食物链

根据题意，森林中有三种动物，我们可以把它看作用并查集维护动物之间关系的一个题目。

重点在于：转化条件为权值。

例如：0 —— 这个节点与它的父节点是同类

1 —— 这个节点被它的父节点吃

2 —— 这个节点吃它的父节点

其实我们的定义不是随便制定的，根据题目中的要求，说话的时候，第一个数字(即下文所说的 $d$ )制订了后面两种动物的关系：

1 —— $X$ 与 $Y$ 同类

2 —— $X$ 吃 $Y$

我们注意到，当 $d = 1$ 的时候， $\left ( d-1 \right ) = 0$ ，也就是我们制定的意义，当 $d=2$ 的时候， $\left ( d-1 \right )=1$ ，代表 $Y$ 被 $X$ 吃，也是我们指定的意义。

确定权值之后，我们要确定有关的操作。我们把所有的动物全部初始化 $relation[i]=0$ ， $f[i]=i$ 。

之后考虑路径压缩，公式就是 $relation[now]=(relation[now]+relation[fa[now]]) \mod3$

可以穷举推，这里我给出穷举过程

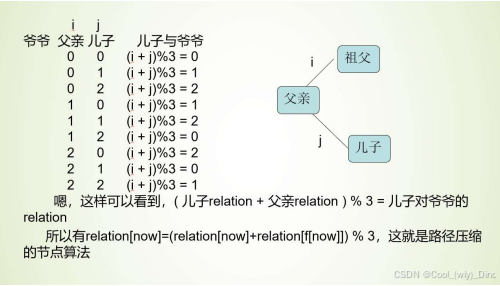
具体来说还是向量三角形的问题，只要画个图考虑就好先可以根据代码理解。

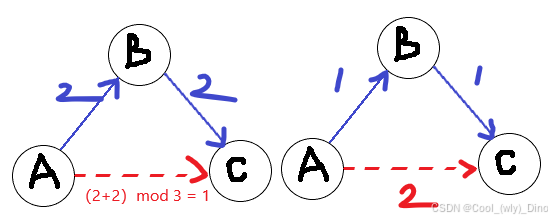
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
namespace Dino
{
	const int N = 2e5+500;
	int n, m, k, cnt = 0;
	int fa[N];
	
	int find(int x)
	{
		if(fa[x] == x) return x;
		return fa[x] = find(fa[x]);
	}
	
	inline void add(int x,int y,int d)
	{
		int fx = find(x);
		int fy = find(y);
		if(d == 1)
		{
			if(fx != fy && fx != find(y+n) && fx != find(y+2*n))
			{
				fa[fx] = fy;
				fa[find(x+n)] = find(y+n);
				fa[find(x+2*n)] = find(y+2*n);
			}else if(fx == find(y+n) || fx == find(y+2*n)){
				cnt++;
			}
		}else{
			if(fx != fy && fx != find(y+n) && fx != find(y+2*n))
			{
				fa[fx] = find(y+2*n);
				fa[find(x+n)] = fy;
				fa[find(x+2*n)] = find(y+n);
			}else if(fx == fy || fx == find(y+n))
			{
				cnt++;
			}
		}
	}
	
	auto work=[]()
	{
		cin >> n >> k;
		for(int i=1; i <= 3*n; i++) fa[i] = i;
		for(int i=1,x,y,d; i <= k; i++)
		{
			cin >> d >> x >> y;
			if((d == 2 && x == y) || x > n || y > n)
			{
				cnt++;
				continue;
			}
			add(x,y,d);
		}
		cout << cnt << endl;
	};
}
signed main()
{
	fastio;
	return Dino::work(), 0;
}

不完美的先散花