递归、搜索、回溯

递归算法在C++中的应用

原创已于 2025-10-22 16:56:48 修改 · 932 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #回归算法

于 2025-02-20 10:55:10 首次发布

1.递归

递归是指在函数的定义中使用函数自身的方法。常用于二叉树的遍历，深度优先遍历（DFS）等情况。

（1）那么为什么会用到递归？

因为遇到了相同的子问题，因此使用递归自己调用自己。

（2）如何写好递归？

1. 函数头的设计：先找到相同的子问题

2. 函数体的书写：只关心摸某一个子问题是如何解决的

3. 注意函数出口

（3）如何理解递归？

不要在意递归的细节展开图，把递归的函数当成一个黑盒，相信这个这个黑盒即可。

2. 汉诺塔问题

为什么可以用递归：具有相同的子问题

（1）函数头的设计

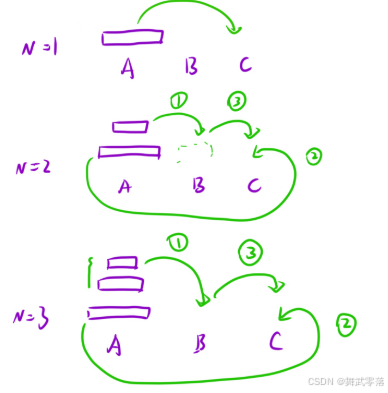
通过dfs函数实现：将A柱子上的一堆盘子借助B移动到Z柱上。

void dfs( A, B, C, int n)

（2）函数体：只关心一个子问题在做什么

1. 将A柱子上的n - 1个盘子借助B移动到Z柱上：dfs(A, B, C, n - 1)

2. 将A柱子上的最后一个盘子移动到c盘上

3. 将B柱子上的n - 1盘子借助A移动到C上：dfs（B, A, C, n - 1）

（3）递归的出口

当只有一个盘子时，直接将盘子移动到C盘，然后返回。

面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）

class Solution {
public:
    void dfs(vector<int>& A, vector<int>& B, vector<int>& C, int n)
    {
        if(n == 1) 
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
        dfs(A, C, B, n - 1);
        C.push_back(A.back());
        A.pop_back();
        dfs(B, A, C, n - 1);
    }
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        dfs(A, B, C, A.size());
    }
};

3.合并两个有序链表

（1）函数头的设计

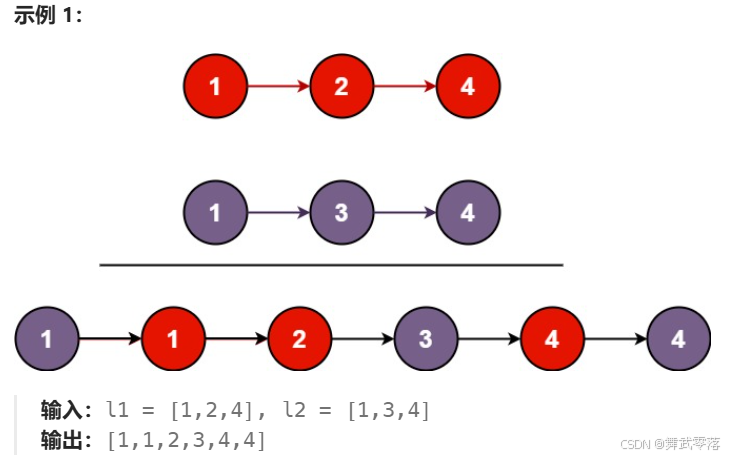
相同的子问题：合并两个链表。dfs(l1, l2)

（2）函数体：只关心一个子问题在做什么

1. 比较节点大小

2. 将较小的节点与合并好的链表连接

3. 返回合并好的链表

（3）递归的出口

当某一链表走到空指针时返回

21. 合并两个有序链表 - 力扣（LeetCode）

class Solution {
public:
    ListNode* dfs(ListNode* l1, ListNode* l2)
    {
        if(l1 == nullptr) return l2;
        if(l2 == nullptr) return l1;

        if(l1->val <= l2 ->val) 
        {
            l1->next = dfs(l1->next, l2);
            return l1;
        }
        else 
        {
            l2->next = dfs(l2->next, l1);\
            return l2;
        }
        
    }
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        return dfs(l1, l2);
    }
};

4. 二叉树剪枝

后序遍历

（1）函数头的设计

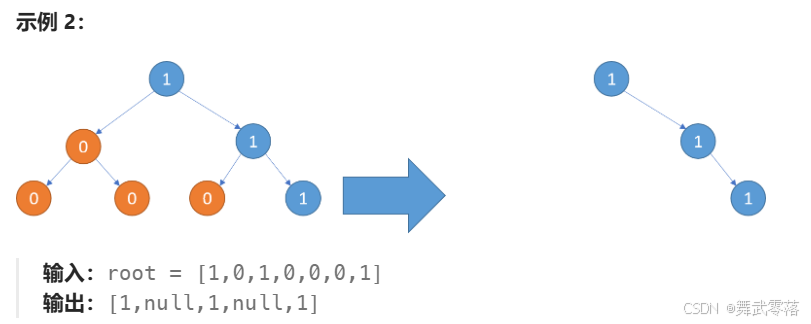
相同的子问题：判断子节点是否为0，为0则剪枝。TreeNode* pruneTree(TreeNode* root)

（2）函数体：只关心一个子问题在做什么

1. 先处理左右子树是否剪枝

2. 判断所在节点的左右节点是否需要剪枝

（3）递归的出口

1. 节点为空

2. 函数体执行结束

814. 二叉树剪枝 - 力扣（LeetCode）

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if(root == nullptr) return nullptr;

        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);

        if(root->left == nullptr && root->right == nullptr && root->val == 0) 
            root = nullptr;
        return root;
    }
};

5.验证二叉树

中序遍历

相同的子问题：判断当前节点所在子树是否是二叉树。

（1）函数头的设计

（2）函数体：只关心一个子问题在做什么

1. 判断左子树是否是二叉搜索树

2. 判断当前节点是否符合二叉搜索树：当前节点的值与其左子树最大的值相比较

3. 判断右子树是否是二叉搜索树

（3）递归的出口

1. 当节点为空

2. 判断当前节点所在子树和其左右子树是否是二叉搜索树之后

class Solution {
public:
    long long prev = LONG_MIN;
    bool isValidBST(TreeNode* root) 
    {
        if(root == nullptr) return true;

        bool left = isValidBST(root->left);
        if(left == false) return false;

        bool cur = false;
        if(root->val > prev) 
        {
            prev = root->val;
            cur = true;
        }
        if(cur == false) return false;
        bool right = isValidBST(root->right);

        return left && right && cur;
    }
};

98. 验证二叉搜索树 - 力扣（LeetCode）

6. 二叉树所有路径

前序遍历

（1）函数头的设计

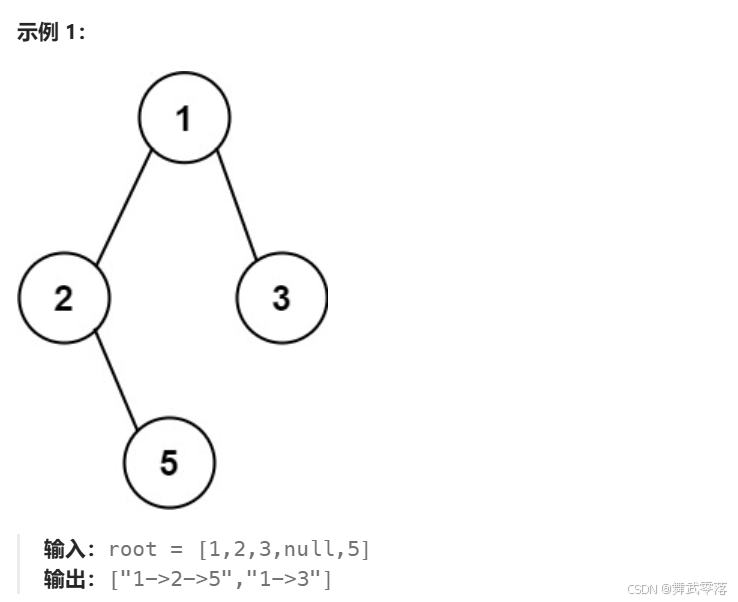
相同的子问题：判断当前节点是否为叶子节点

（2）函数体：只关心一个子问题在做什么

1. 记录下当前的路径

2. 判断当前节点是否是叶子节点，是则记录下此条路径

3. 完成前序遍历

（3）递归的出口

是空节点或遍历到叶子节点后

class Solution {
public:
    vector<string> ret;
    void dfs(TreeNode* root, string path)
    {
        if(root == nullptr) return;

        path += to_string(root->val);
        if(root->left == nullptr && root->right == nullptr) 
        {
            ret.push_back(path);
            return;
        }
        else path += "->";

        dfs(root->left, path);
        dfs(root->right, path);
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        dfs(root, path);
        return ret;
    }
};

257. 二叉树的所有路径 - 力扣（LeetCode）

7. 全排列

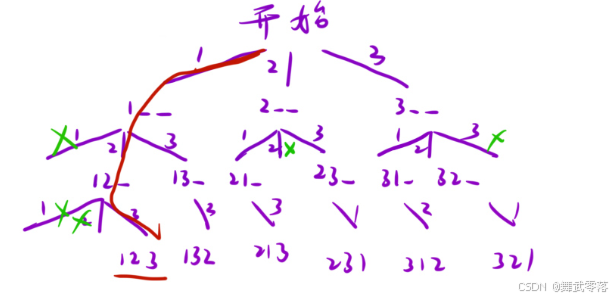
class Solution {
    vector<vector<int>> ret;
    vector<int> path;
    bool check[7];
public:
    void dfs(vector<int> nums)
    {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }
        for(int i = 0; i < nums.size(); i++)
        {
            if(check[i] == false)
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums);
                //回溯
                path.pop_back();
                check[i] = false;
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        dfs(nums);
        return ret;
    }
};

46. 全排列 - 力扣（LeetCode）

8.子集

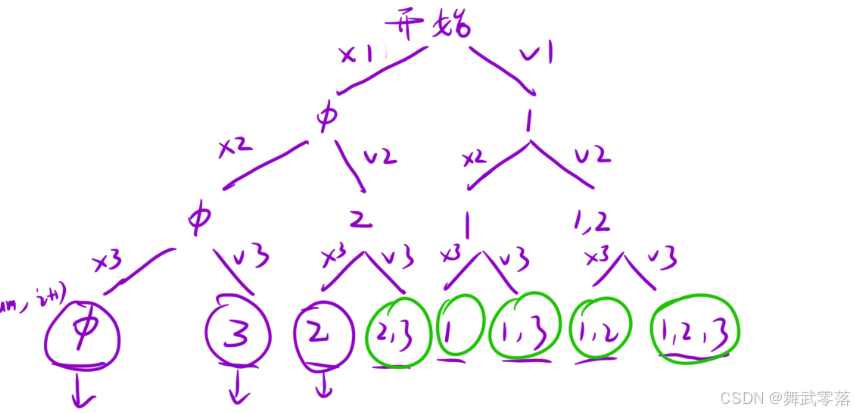
class Solution {
    vector<vector<int>> ret;
    vector<int> path;
public:
    void dfs(vector<int>& nums, int i)
    {
        if(i == nums.size())
        {
            ret.push_back(path);
            return;
        }
        path.push_back(nums[i]);
        dfs(nums, i + 1);
        path.pop_back();

        dfs(nums, i + 1);
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }
};

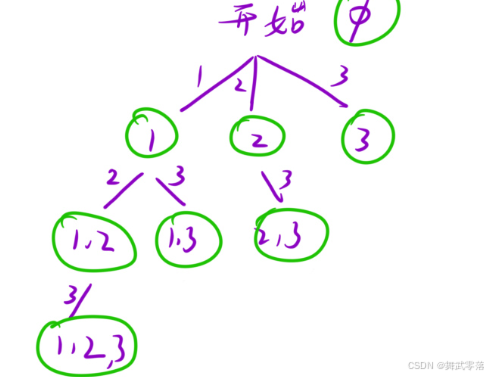
class Solution {
    vector<vector<int>> ret;
    vector<int> path;
public:
    void dfs(vector<int>& nums, int pos)
    {
        ret.push_back(path);
        for(int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            dfs(nums, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }
};

78. 子集 - 力扣（LeetCode）