面试常见算法

俗话说面试造火箭，工作拧螺丝，IT人必须接受这个现实问题。

一般的面试过程中，即便学历、行业背景、年龄、距离、开发语言、技术栈、项目经历等细节都合适，可能在写算法这一关错过。说明算法是很重要的，数据结构，五大常用算法：分治法，贪心算法，动态规划，分支限界法等还是复习一下为好。LeetCode刷题。

时间复杂度是一个算法运行所需要的时间。

空间复杂度是一个算法运行所需要的储存空间。

一  二叉树

二叉树生成（先序或层次）

非递归遍历算法思想：

层次：根节点入队列开始循环，输出当前节点，出队列，左儿子入队列（不为空的话），右儿子出队列（不为空的话）

先序：根节点入栈开始循环，输出当前节点，右节点入栈，左节点入栈

中序：根节点入栈开始循环，一直找左儿子，依次入栈。最后一个左儿子输出，出栈，访问此时栈顶的父节点，出栈；针对右儿子子树，继续前边的循环。出栈的时候，需要记录右子树已遍历过。

后序：可以先得到逆后序遍历，入栈2，再出栈。  逆后序遍历像先序遍历，不过一直先访问右儿子，再访问左儿子。

平衡树是为了解决二叉查找树退化为链表的情况。

性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

红黑树是为了解决平衡树在插入、删除等操作需要频繁调整的情况。

 

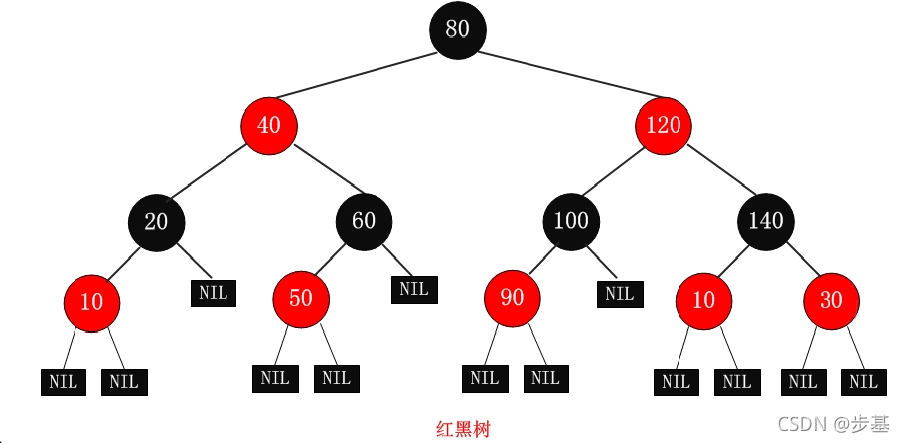
红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：
(01) 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
(02) 特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

二  排序

int a[7] = {3, 8, 1, 9, 2, 5, 4};   //下方代码使用

1 快速算法思想：

以数组第一个数作为key = a[0];

j从右往左查找第一个a[j]>=a[0],j--

i从左往右查找第一个a[i]>=a[0],i++

此时swap(a[i],a[j])

退出循环时swap(a[i],a[0])，i位置左边都是小于key的数，右边都是大于key的数

时间复杂度：

最好：O ( n *l o g  n ) 
最坏：O ( n 2 ) 
平均：O ( n* l o g  n ) 
空间复杂度：O ( n* l o g  n ) 

稳定性：不稳定

2 归并排序

归并排序要点在于合并merge，分治法递归mergeSort反而实现简单。

//////////////////归并排序//////////////////////

void merge(int a[], int begin, int mid, int end){

    int left = begin, right = mid + 1, k = end;

    int *tmp = new int[end - begin + 1]; //新开辟临时数组

    int i = 0;

    while (left < right)    {

        while (left <= mid && right <= end)

            tmp[i++] = a[left] <= a[right] ? a[left++] : a[right++];

        //其中一个数组已排序完成

        while (left <= mid)

            tmp[i++] = a[left++];

        while (right <= end)

            tmp[i++] = a[right++];

    }

    for (i = 0; i < end - begin + 1; i++)    {

        a[begin + i] = tmp[i];

        cout << "a[i]" << a[i] << endl;

    }

    delete[] tmp;

}

void mergeSort(int a[], int begin, int end){

    if (begin == end)        return;

    int mid = (begin + end) / 2;

    mergeSort(a, begin, mid); //分治排序

    mergeSort(a, mid + 1, end);

    merge(a, begin, mid, end); //合并

}

3 单链表逆序

单链表逆序头插法，after节点插到cur前边。须注意after->next是否有节点即可。

pre

head          cur             after         *         *        *

////////////////////////单链表逆序/////////////////////////////

//链表节点

struct linkNode

{

    int iData;

    linkNode *next;

    linkNode()

    {

        iData = 0;

        next = NULL;

    }

};

//创建链表

linkNode *createLink(int a[], int iCount){

    linkNode *head = new linkNode;

    linkNode *cur = head;

    for (int i = 0; i < iCount; i++)    {

        cur->next = new linkNode;

        cur->next->iData = a[i];

        cur = cur->next;

    }

    return head;

}

void reverse(linkNode *head){

    linkNode *pre = head;

    linkNode *cur;

    linkNode *after;

    while (pre->next)

    {

        cur = pre->next;

        after = cur->next;

        pre->next = after;

        //头插法

        if (after->next)

        {

            pre->next = after;

            pre = after;

            after = after->next;

            pre->next = cur;

            cur->next = after;

        }

        else

        {

            after->next = cur;

            cur->next = NULL;

            return;

        }

    }

}

三 top k问题

算法思想：

先做1趟快排，确定k在基准key的左侧还是右侧，再部分快速排序。

例如：4    3      8      6        7     5       1      9     2

查找第3大的数。k=3

第一趟快排结果   2   3   1                  6       7      5     8     9     4

第3大的数在排序右侧中查找

第二趟快排结果         6   4   5              8    9   7

第3大的数在排序右侧中查找，此时只需对8    9     7排序，取第3大的数即可

四  五大常用算法

分治法与动态规划法

与分治法类似，动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}

分支限界法与回溯法

1. 求解目标：回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。

2. 搜索方式的不同：回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

常见的两种分支限界法：

1. 队列式(FIFO)分支限界法
   按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。
2. 优先队列式分支限界法
   按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。

例如最短路径