import java.util.ArrayList;
import java.util.Collections;
public class Sort {
public static void main(String[] args) {
}
// 1、冒泡排序
// 从最后一个索引位置开始,每次确定一个位置的数,保证后半段有序
// 第二层循环是从最前面一个一个比较,直到有序的位置
public static void bubbleSort(int[] nums){
for(int i = nums.length - 1; i > 0; i--){
for(int j = 0; j < i; j++){
if(nums[j] > nums[j + 1]){
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
// 1-2、冒泡排序优化
// 在冒泡排序的基础上增加一个标志位,如果前一轮没有进行交换,说明数组已经有序
public static void bubbleSortPro(int[] nums){
for(int i = nums.length - 1; i > 0; i--){
boolean flag = false;
for(int j = 0; j < i; j++){
if(nums[j] > nums[j + 1]){
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
flag = true;
}
}
if(!flag){
break;
}
}
}
// 2、选择排序
// 依次找出当前无序的里面最小的,放到有序半段的末尾,保证前半段有序
public static void selectionSort(int[] nums){
for(int i = 0; i < nums.length - 1; i++){
int min = i;
for(int j = i + 1; j < nums.length; j++){
if(nums[j] < nums[min]){
min = j;
}
}
if(i != min){
int tmp = nums[i];
nums[i] = nums[min];
nums[min] = tmp;
}
}
}
// 3、插入排序
// 从第二个元素开始,在有序子数组中查找该元素的合适位置并插入
public static void insertionSort(int[] nums){
for(int i = 1; i < nums.length; i++){
int tmp = nums[i];
int j = i;
while(j > 0 && tmp < nums[j - 1]){
nums[j] = nums[j - 1];
j--;
}
if(j != i){
nums[j] = tmp;
}
}
}
// 4、希尔排序
// 插入排序的改进版本,增加了步长的
// 将整个待排序的序列分割成若干子序列并分别进行插入排序,基本有序后再整体依次插入排序
// 通过不同长度的step,每次保证局部有序,逐步缩短step,然后最终实现整体有序
public static void shellSort(int[] nums) {
for (int step = nums.length / 2; step >= 1; step /= 2) {
for (int i = step; i < nums.length; i++) {
int temp = nums[i];
int j = i - step;
while (j >= 0 && nums[j] > temp) {
nums[j + step] = nums[j];
j -= step;
}
nums[j + step] = temp;
}
}
}
// 5、归并排序
// 分治算法的经典应用
public static void mergeSort(int[] nums){
int[] tmp = new int[nums.length];
internalMergeSort(nums, tmp, 0, nums.length - 1);
}
private static void internalMergeSort(int[] nums, int[] tmp, int left, int right) {
if(left < right){
int mid = (left + right) >>> 1;
internalMergeSort(nums, tmp, left, mid);
internalMergeSort(nums, tmp, mid + 1, right);
mergeSortedArray(nums, tmp, left, mid, right);
}
}
private static void mergeSortedArray(int[] nums, int[] tmp, int left, int mid, int right) {
int i = left, j = mid + 1, k = 0;
while(i <= mid && j <= right){
tmp[k++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
}
while(i <= mid){
tmp[k++] = nums[i++];
}
while(j <= right){
tmp[k++] = nums[j++];
}
for (int l = 0; l < k; l++) {
nums[left + l] = tmp[l];
}
}
// 6、快排
public static void quickSort(int[] nums){
qSort(nums, 0, nums.length - 1);
}
private static void qSort(int[] nums, int lo, int hi) {
if(lo >= hi){
return;
}
int m = partition(nums, lo, hi);
qSort(nums, lo, m - 1);
qSort(nums, m, hi);
}
private static int partition(int[] nums, int lo, int hi){
int i = lo, j = hi + 1;
while(true){
while(++i <= hi && nums[i] < nums[lo]);
while(--j >= lo && nums[j] > nums[lo]);
if(i >= j){
break;
}
swap(nums, i, j);
}
swap(nums, lo, j);
return i;
}
private static void swap(int[] nums, int lo, int j) {
int tmp = nums[lo];
nums[lo] = nums[j];
nums[j] = tmp;
}
// 7、堆排序
public class ArrayHeap {
private int[] arr;
public ArrayHeap(int[] arr) {
this.arr = arr;
}
private int getParentIndex(int child) {
return (child - 1) / 2;
}
private int getLeftChildIndex(int parent) {
return 2 * parent + 1;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/**
* 调整堆。
*/
private void adjustHeap(int i, int len) {
int left, right, j;
left = getLeftChildIndex(i);
while (left <= len) {
right = left + 1;
j = left;
if (j < len && arr[left] < arr[right]) {
j++;
}
if (arr[i] < arr[j]) {
swap(arr, i, j);
i = j;
left = getLeftChildIndex(i);
} else {
break; // 停止筛选
}
}
}
/**
* 堆排序。
* */
public void sort() {
int last = arr.length - 1;
// 初始化最大堆
for (int i = getParentIndex(last); i >= 0; --i) {
adjustHeap(i, last);
}
// 堆调整
while (last >= 0) {
swap(arr, 0, last--);
adjustHeap(0, last);
}
}
}
// 8、计数排序
public static void countSort(int[] a, int max, int min) {
int[] b = new int[a.length];//存储数组
int[] count = new int[max - min + 1];//计数数组
for (int num = min; num <= max; num++) {
//初始化各元素值为0,数组下标从0开始因此减min
count[num - min] = 0;
}
for (int i = 0; i < a.length; i++) {
int num = a[i];
count[num - min]++;//每出现一个值,计数数组对应元素的值+1
}
for (int num = min + 1; num <= max; num++) {
//加总数组元素的值为计数数组对应元素及左边所有元素的值的总和
count[num - min] += a[num - min - 1];
}
for (int i = 0; i < a.length; i++) {
int num = a[i];//源数组第i位的值
int index = count[num - min] - 1;//加总数组中对应元素的下标
b[index] = num;//将该值存入存储数组对应下标中
count[num - min]--;//加总数组中,该值的总和减少1。
}
//将存储数组的值一一替换给源数组
for(int i=0;i<a.length;i++){
a[i] = b[i];
}
}
// 9、桶排序
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
System.out.println(bucketArr.toString());
}
}
/**
* 10、基数排序
* 考虑负数的情况还可以参考: https://code.i-harness.com/zh-CN/q/e98fa9
*/
public class RadixSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
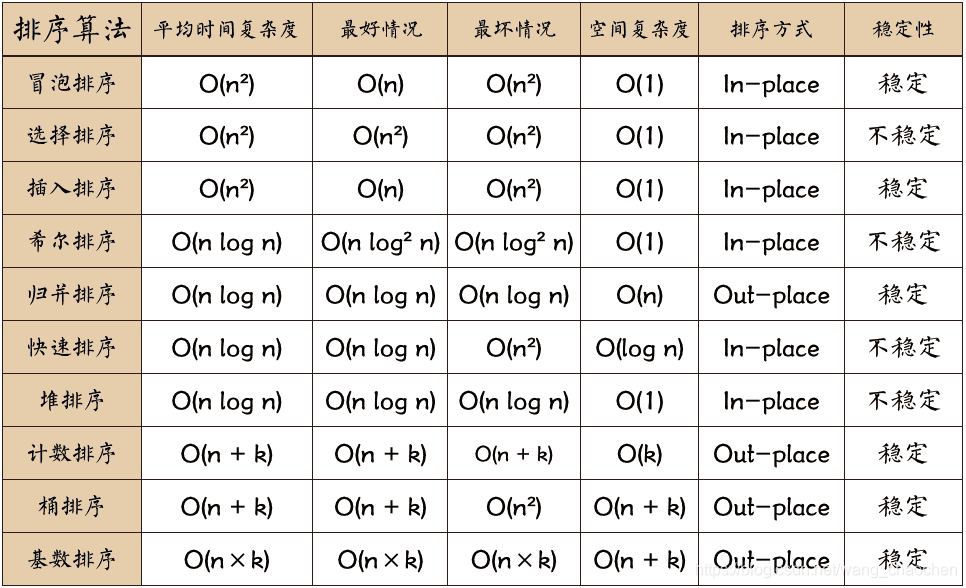
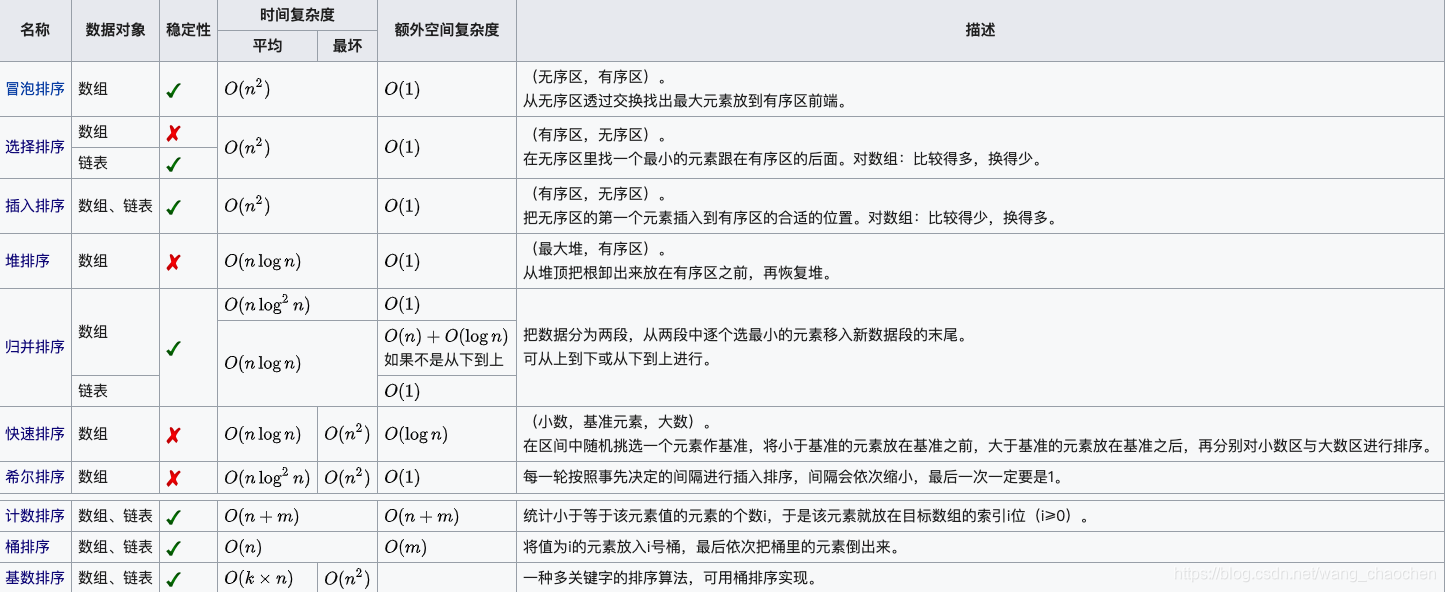
Java十大排序算法实现
最新推荐文章于 2022-12-27 15:38:40 发布





















 921
921

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








