并查集之云宗的分分合合

你好吖~

我们来聊一聊并查集吧。

一、何为并查集

并查集，从字面理解，即“对于集合进行合并与查询的操作”。它是一种树形数据结构，用于处理一些不相交的集合的合并与查询工作。

• 合并：将两个集合合二为一
• 查询：询问两个 元素是否在同一集合中

接下来，我们一起来理解一下这两个操作。

二、“并查集”之合并

红云是红派掌门，绿云是绿派掌门。现在，红派被绿派吞并，组成了一个新的门派——云宗。               ——《云宗的历史》

红绿搭配，干活不累。 

我们来分析一下这段文字。

1. 红派、绿派和云宗，都是集合，都可以依据某些关系形成一棵树。门徒是集合中的元素。
2. 红云是“红派”集合的“根节点”，绿云是“绿派”集合的“根节点”，同时也是“云宗”集合的根节点。
3. 门派间的吞并 = 集合间的合并

到底怎么合并呢？我们画个图演示一下。

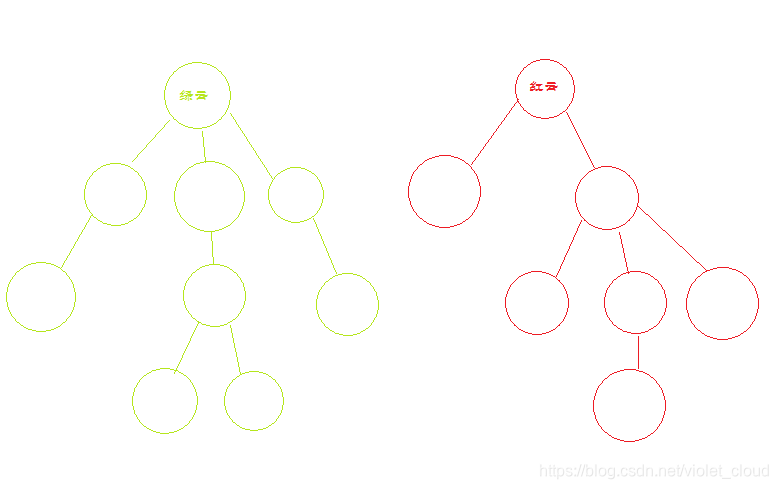
 此时绿派吞并红派。

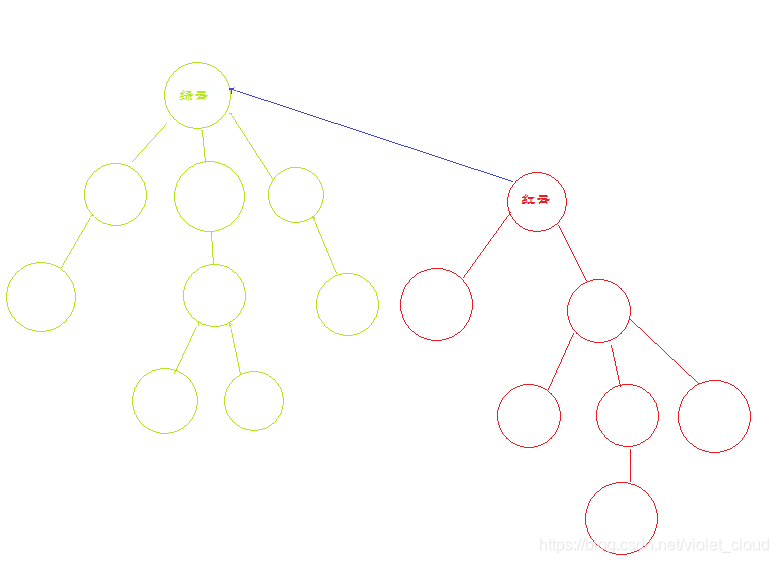
形成了云宗。

我们经过观察发现，进行合并操作，只是将红云的上司设成绿云——给他安了个父亲结点。

我们用箭头表示一下“父子关系”，箭头所指为“父节点”。

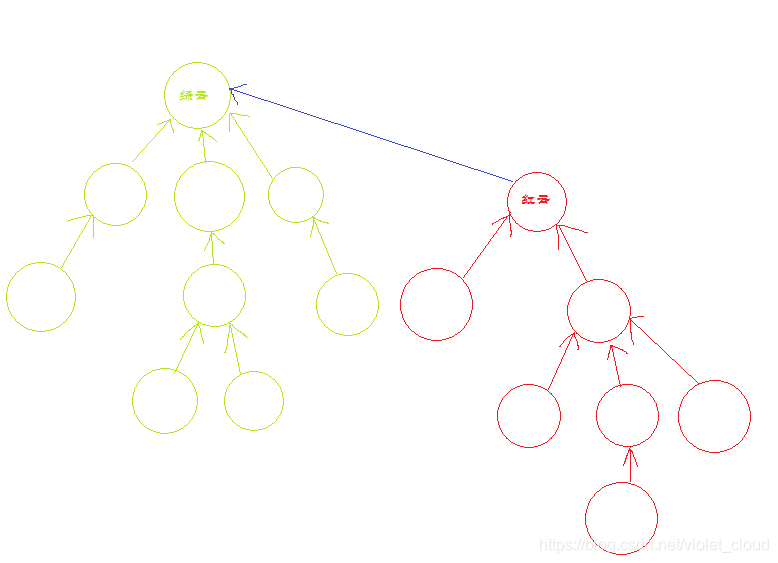
两个门派分别有自己的指向关系，而合并后，红云的“父亲”就成了绿云。 

也就是说，对于A、B两个集合，将集合A的根节点 设为集合B的根节点的子节点，这样的操作就是合并。

三、“并查集”之查询

千年后，云宗分裂为以橙云为首的橙门和以蓝云为首的蓝门。                ——《云宗的历史》

我们把两个门派的关系树列出来。

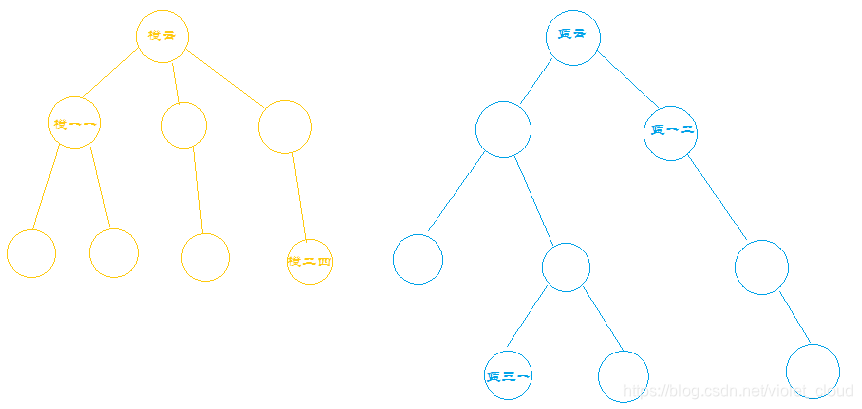
 1）询问橙一一和橙二四是否在同一门派

        法一：看名字

                        废话，但普通题目才没有这种特性呢。

        法二：搜索

                        以橙一一（或橙二四为起点），遍历整个集合，看能不能搜到对方。

                        很复杂。

        ……

        法N：看掌门

                        一个门派只有一个掌门，即一棵树只有一个根节点，如果两者在同一集合内，则两

                        者的根节点必定相同。换句话说，如果两者的根节点相同，那么两者在同一集合

                        内。

我们来演示一下。

2）询问橙一一和蓝三一是否在同一门派

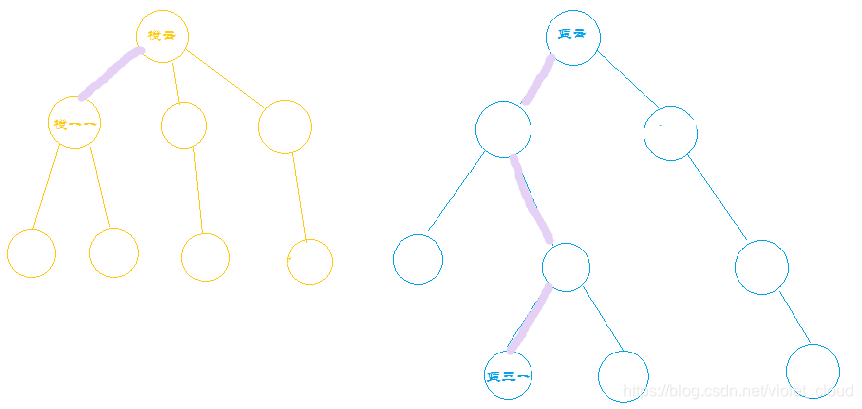
我们让两人沿着紫色的路径找到所在的树的根节点。

我们发现根节点橙云和根节点蓝云不是同一个人（哪怕是孪生兄弟也不是同一个人好叭） ，所以橙一一和蓝三一不在同一集合中。

3）询问蓝一二和蓝三一是否在同一门派

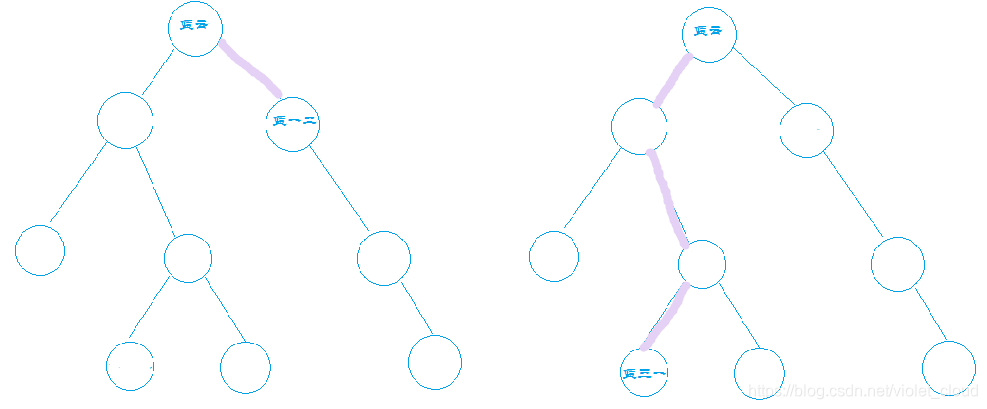
我们再次让两人沿着紫色路径找所在树的根节点。

很好，根节点蓝云和根节点蓝云是同一个人（也有可能只是名字相同好叭） ，所以蓝一二和蓝三一在同一集合内。

经过以上讲解，你是否理解了并查集的基本操作呢？

快去打一道模板题练练手吧。

题目传送门：洛谷P3367 【模板】并查集

题解通道：洛谷P3367 【模板】并查集 题解

读者：你没有附代码。

我：自己看我的题解叭。