上一节的HAN表示异构图的Attention Network,通过手动设置Meta-path,然后聚合不同Meta-path下的节点attention,学到节点最终的表示。但是这个方法是手动选择Meta-path的,因此可能无法捕获每个问题的所有有意义的关系。同样,元路径的选择也会显著影响性能
而Graph Transformer Networks是自动聚合Meta-path,同时以端到端的学习方式转换图上的节点表示形式。
几个概念
- τv\tau ^vτv:节点的类型
- τe\tau^eτe:边的类型
- ACM数据集包含:Paper(3025),Author(5835),Subject(56)个类型,τv=3,τe={PA,AP,PS,SP}\tau^v=3,\tau^e = \{PA, AP, PS, SP\}τv=3,τe={PA,AP,PS,SP},需要注意的是Author和Subject之间没有边的连接, 所以没有AS和SA的关系。
- {Ak}kK=1,K=∣τe∣\{A_k\}^K_k=1, K = |\tau^e|{Ak}kK=1,K=∣τe∣:邻接矩阵,例如Paper与Author的邻接矩阵的大小是3025×58353025 \times 58353025×5835,而Paper与Subject的邻接矩阵的大小是3025×563025 \times 563025×56,因此这两个邻接矩阵的shape大小不同。为了把shape统一到一起,需要将节点组合在一起,形成统一的一个邻接矩阵。如下图所示蓝色的部分就是PA的邻接矩阵,其余的地方数据为0,表示没有边的连接
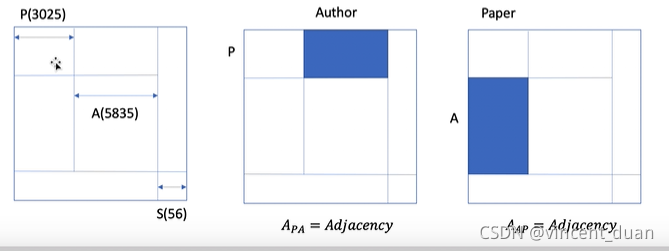
- 特征矩阵: 每个Paper都有自己的特征,例如
Paper1 = [1,0,0,0,1,1,0,....,0,0],Paper2=[1,1,0,1,0,1,0,.....,0,0],而Author的特征是将对应的Paper特征拼在一起,例如Author1 = [Paper1, Paper2]=[1,1,0,1,0,1,0,....,0,0],同理Subject也是将对应的Paper拼在一起,例如Subject1 = [Paper1, Paper3] = [1,1,0,1,1,1,0...,0,0]。需要注意的是,这里并不一定是要拼接在一起,可以做均值Pooling、或者max pooling、或者求和,可以根据自己的任务来选择。
GTN如何组合多元的Meta-path的
已知τe={PA,AP,PS,SP}\tau^e=\{PA,AP,PS,SP\}τe={PA,AP,PS,SP},想得到PAP这个Meta-path下,所形成的Paper和Paper之间的邻接矩阵,那么就可以做AdjPA∗AdjAPAdj_{PA} * Adj_{AP}AdjPA∗AdjAP,也就是meta-path={PAP}={PA,AP}=AdjPA∗AdjAP\{PAP\}=\{PA, AP\}=Adj_{PA} * Adj_{AP}{PAP}={PA,AP}=AdjPA∗AdjAP,矩阵的相乘相当于节点的转移,通过A节点得到P节点之间的连接关系。
反之,如果meta-path={PAP}={PA,PA}=AdjPA∗AdjPA\{PAP\}=\{PA, PA\}=Adj_{PA} * Adj_{PA}{PAP}={PA,PA}=AdjPA∗AdjPA,这样是没有一个具体的物理意义,同理{PA,PS},{AP,SP}=Nan\{PA,PS\},\{AP,SP\}=Nan{PA,PS},{AP,SP}=Nan,(在邻接矩阵上相乘得到0矩阵)。
meta-path={APA}={AP,AP}=AdjAP∗AdjAP=AA\{APA\}=\{AP, AP\}=Adj_{AP} * Adj_{AP}={AA}{APA}={AP,AP}=AdjAP∗AdjAP=AA得到的和Paper无关,因为我们的任务是做Paper的分类,对结果没有影响。
算法流程

矩阵A表示多种Meta-path下的邻接矩阵,利用可学习的参数wϕ1w_\phi^1wϕ1做softmax,得到的向量,与矩阵A相乘
例如:τe={t1,t2,t3,t4}\tau^e=\{t_1,t_2, t_3,t_4\}τe={t1,t2,t3,t4},有四个邻接矩阵A={A1,A2,A3,A4}A = \{A_1, A_2,A_3,A_4\}A={A1,A2,A3,A4},创建四个可学习的参数Wϕ1={α11,α21,α31,α41},Wϕ2={α12,α22,α32,α42}W_\phi^1=\{\alpha_1^1, \alpha_2^1,\alpha_3^1,\alpha_4^1\},W_\phi^2=\{\alpha_1^2, \alpha_2^2,\alpha_3^2,\alpha_4^2\}Wϕ1={α11,α21,α31,α41},Wϕ2={α12,α22,α32,α42},然后将Wϕ1W_\phi^1Wϕ1和Wϕ2W_\phi^2Wϕ2做一次softmax,然后与邻接矩阵相乘,得到Q1=α11∗A1+α21∗A2+α31∗A3+α41∗A4Q_1=\alpha_1^1 * A_1 + \alpha_2^1 * A_2 + \alpha_3^1 * A_3+\alpha_4^1 * A_4Q1=α11∗A1+α21∗A2+α31∗A3+α41∗A4相当于对A矩阵进行了一次加权求和,同理得到Q2Q_2Q2矩阵,然后将Q1Q_1Q1与Q2Q_2Q2相乘的到A1=Q1∗Q2A^1 = Q_1 * Q_2A1=Q1∗Q2,A1A_1A1相当于聚合了一次Meta-path之后的到的邻接矩阵,也就是上面讲的meta-path={PAP}={PA,PA}=AdjPA∗AdjPA\{PAP\}=\{PA, PA\}=Adj_{PA} * Adj_{PA}{PAP}={PA,PA}=AdjPA∗AdjPA
如果要学习任意长度的Meta-path,那么可以学习多个channel,这样就学习出多个Meta-path下的聚合方式,
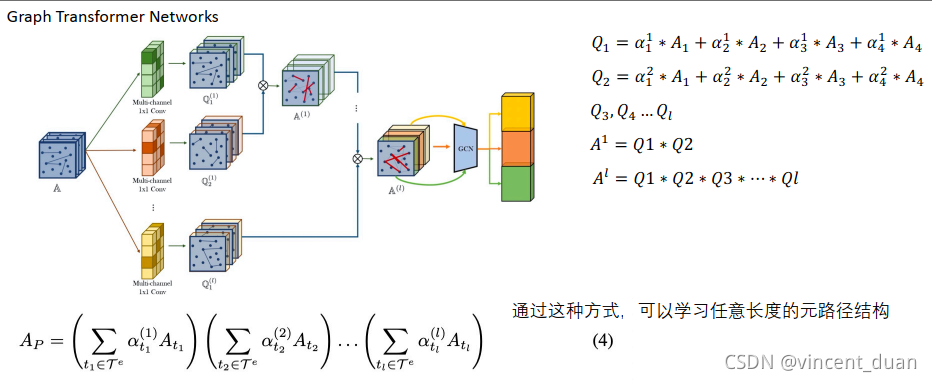





 GraphTransformerNetworks(GTN)是一种自动聚合异构图中Meta-path的方法,相较于手动设置Meta-path,GTN能以端到端的方式学习节点表示。在ACM数据集中,它处理Paper、Author和Subject三种类型的节点及不同类型的边。GTN通过矩阵运算组合多元Meta-path,例如,通过 Adj_{PA}
GraphTransformerNetworks(GTN)是一种自动聚合异构图中Meta-path的方法,相较于手动设置Meta-path,GTN能以端到端的方式学习节点表示。在ACM数据集中,它处理Paper、Author和Subject三种类型的节点及不同类型的边。GTN通过矩阵运算组合多元Meta-path,例如,通过 Adj_{PA}
















 1490
1490

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








