为了解决TransE模型在处理一对多 、 多对一 、多对多复杂关系时的局限性,TransH模型提出让一个实体在不同的关系下拥有不同的表示。如下公式所示,对于关系rrr,TransH模型同时使用平移向量rrr和超平面的法向量wrw_rwr来表示它。对于一个三元组(h,r,t)(h, r, t)(h,r,t) , TransH首先将头实体向量hhh和尾实体向量rrr,沿法线wrw_rwr,映射关系rrr对应的超平面上,用h⊥h_\perph⊥和t⊥t_\perpt⊥表示如下:
h⊥=h−wr⊤hwrt⊥=t−wr⊤twr
h_\perp=h-w_r^\top hw_r \\
t_\perp = t - w_r ^ \top tw_r
h⊥=h−wr⊤hwrt⊥=t−wr⊤twr
需要注意的是,由于关系r:可能存在无限个超平面,TransH简单地令r与w_r,近似正交来选取某一个超平面。TransH 使不同的实体在不同的关系下拥有了不同的表示形式,但由于实体向量被投影到了关系的语义空间中,故它们具有相同的维度。
我们可以通过先下面这图来进一步加深对这个超平面概念的理解:
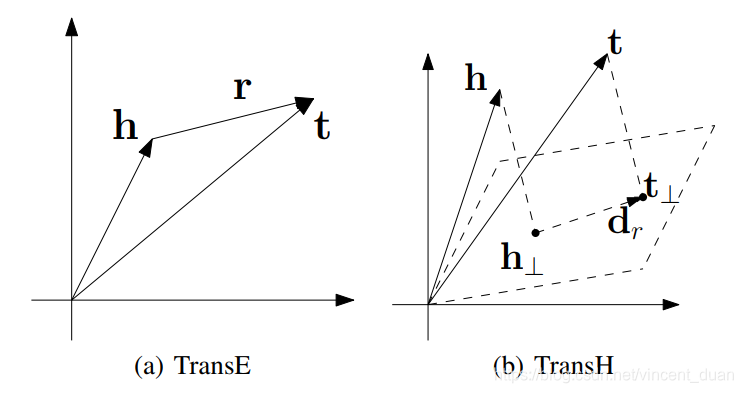
根据上图,我们可以得一个三元组元素的数学表示,h和t分别代表头结点和尾节点的向量,而关系超平面由平面的法向量wrw_rwr以及平面上的平移向量 drd_rdr表示。
具体的算法实现,对于一个三元组,我们首先需要将h和t映射到我们的超平面上,从而得到映射向量 [公式] 和 [公式] , 具体公式如下:
h⊥=h−wr⊤hwrt⊥=t−wr⊤twr
h_\perp=h-w_r^\top hw_r \\
t_\perp = t - w_r ^ \top tw_r
h⊥=h−wr⊤hwrt⊥=t−wr⊤twr
其中简单说明下wr⊤hwrw_r^\top h w_rwr⊤hwr的含义,这里wr⊤h=∣w∣∣h∣cosθw_r^\top h = | w| |h|cos\thetawr⊤h=∣w∣∣h∣cosθ表示hhh在wrw_rwr方向上投影的长度(带正负号),乘以wrw_rwr即hhh在wrw_rwr上的投影。
得到投影之后,我们就可以根据下面的score function来求得三元组的差值:
fr(h,t)=∣∣(h−wr⊤hwr)+dr−(t−wr⊤twr)∣∣22
f_r(h,t) = || (h-w_r^\top hw_r) +d_r-(t - w_r ^ \top tw_r) ||_2^2
fr(h,t)=∣∣(h−wr⊤hwr)+dr−(t−wr⊤twr)∣∣22
这个公式中所期望的结果为,如果三元组关系是正确的,则结果数值较小,反之则结果数值较大。
为了实现上述所期望的结果,作者引入了margin-base ranking function 作为损失函数来训练模型:
L=∑(h,r,t)∈Δ∑(h′,r′,t′)∈Δ(h′,r′,t′)[fr(h,t)+γ−fr′(h′+t′)]+
\mathcal{L}=\sum_{(h,r,t) \in \Delta} \sum_{(h^\prime,r^\prime,t^\prime) \in \Delta _{(h^\prime,r^\prime,t^\prime)}} [f_r(h,t) + \gamma -f_{r^\prime}(h^\prime + t^\prime) ]_+
L=(h,r,t)∈Δ∑(h′,r′,t′)∈Δ(h′,r′,t′)∑[fr(h,t)+γ−fr′(h′+t′)]+
其中,[x]+[x]+[x]+看做max(0,x)max(0,x)max(0,x),Δ\DeltaΔ表示正确三元组的集合,Δ′\Delta ^\primeΔ′表示负例集合,γ\gammaγ为margin值用于区分正例和负例。这个loss通过Mini-SGD进行训练,需要强调的一点是,训练过程中,需要让fr(h,t)f_r(h,t)fr(h,t)尽可能的小,fr′(h′,t′)f_{r^\prime}(h^\prime,t^\prime)fr′(h′,t′)尽可能大。
除此之外,在最小化loss function的过程中,模型还需要遵循三个软约束原则:
∀e∈E,∣∣e∣∣2≤1,//scale(1)∀r∈R,∣wr⊤dr∣/∣∣dr∣∣2≤ϵ,//orthogonal(2)∀r∈R,∣∣wr∣∣2=1,//unitnormalvector(3)
\forall e \in E, ||e||_2 \leq 1, // scale (1) \\
\forall r \in R, |w_r^\top d_r| /||d_r||_2 \leq \epsilon, //orthogonal (2)\\
\forall r \in R, ||w_r||_2=1,//unit normal vector (3)
∀e∈E,∣∣e∣∣2≤1,//scale(1)∀r∈R,∣wr⊤dr∣/∣∣dr∣∣2≤ϵ,//orthogonal(2)∀r∈R,∣∣wr∣∣2=1,//unitnormalvector(3)
公式一是保证所有实体的embedding都归一化。
公式二则用于保证wrw_rwr和drd_rdr正交垂直,保证drd_rdr在超平面上。
公式三则保证法向量的模为1。
为了体现上面三个约束条件,需要对loss function进行修改,加上对公式一和公式二的约束:
L=∑(h,r,t)∈Δ∑(h′,r′,t′)∈Δ(h′,r′,t′)[fr(h,t)+γ−fr′(h′+t′)]++C{∑e∈E[∥e∥22−1]++∑r∈R[(wr⊤dr)2∥dr∥22−ϵ2]+}(4)
\mathcal{L} = \sum_{(h,r,t) \in \Delta} \sum_{(h^\prime,r^\prime,t^\prime) \in \Delta _{(h^\prime,r^\prime,t^\prime)}} [f_r(h,t) + \gamma -f_{r^\prime}(h^\prime + t^\prime) ]_+ + C \left\{ \sum _{e \in E} \left[ \left \| e\right \| _2^2 -1 \right ] _+ + \sum_{r \in R}\left [ \frac {(w_r^\top d_r)^2}{\left \| d_r \right \| _2^2} - \epsilon ^2 \right ] _+ \right\} \\(4)
L=(h,r,t)∈Δ∑(h′,r′,t′)∈Δ(h′,r′,t′)∑[fr(h,t)+γ−fr′(h′+t′)]++C{e∈E∑[∥e∥22−1]++r∈R∑[∥dr∥22(wr⊤dr)2−ϵ2]+}(4)
其中C表示软约束的权重,它也是训练过程中的一个超参数。
而公式三则是在每次Mini-SGD后,对 wrw_rwr结果进行归一化实现。
最后,TransH与TransE还有一点不同之处,在于负例的生成。现实中的知识图谱不完整,需要减少假负例(即替换了一个节点后的三元组,恰好是整个知识图谱中存在的另一个三元组)的出现,因此需要根据头尾节点关系,进行节点替换,比如,对于一对多的关系,我们更多的替换头结点而不是尾节点,这样才能避免假负例出现的情况,具体的标准如下:
对于一个关系rrr, 我们首先要统计两个数值,即这个关系每个头结点平均对应的尾节点数,记做tphtphtph;及这个关系每一个尾节点平均对应的头节点数,记做 hpthpthpt 。最后通过公式p=tphtph+hptp=\frac{tph}{tph+hpt}p=tph+hpttph来表示头结点被替换的概率,而尾节点替换的概率为1−p1-p1−p
相比于transE, TransH新增了很多参数,使得loss 在SGD中求梯度变得更为复杂,下面简单介绍下,各个参数梯度求解结果。首先Loss 可以分解为一下三个式子:
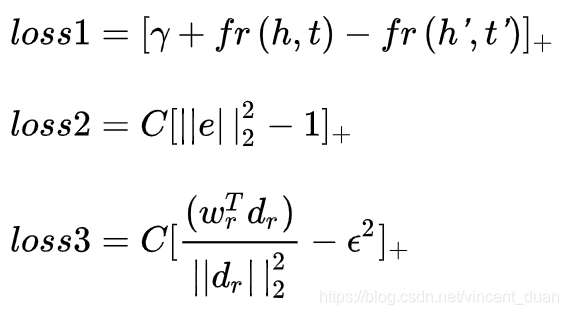
其中Loss1的各参数求导如下:
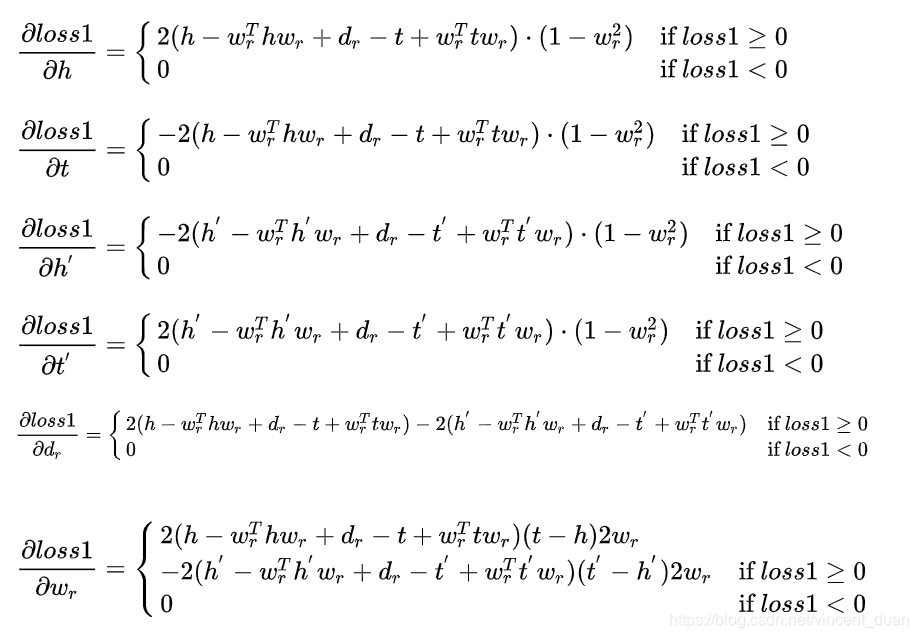
 TransH模型:实体关系表示学习的改进
TransH模型:实体关系表示学习的改进





 TransH模型针对TransE在处理复杂关系时的局限性进行了改进,提出了实体在不同关系下有不同的表示。通过超平面和法向量,实体向量被映射到关系对应的超平面上,使得不同实体在不同关系下有独特表示。模型通过损失函数和软约束进行训练,确保实体向量归一化、关系向量与法向量正交等。训练过程中采用margin-based ranking function,并调整负例生成策略,降低假负例出现。TransH的优化增加了模型复杂性,但增强了对知识图谱中复杂关系的建模能力。
TransH模型针对TransE在处理复杂关系时的局限性进行了改进,提出了实体在不同关系下有不同的表示。通过超平面和法向量,实体向量被映射到关系对应的超平面上,使得不同实体在不同关系下有独特表示。模型通过损失函数和软约束进行训练,确保实体向量归一化、关系向量与法向量正交等。训练过程中采用margin-based ranking function,并调整负例生成策略,降低假负例出现。TransH的优化增加了模型复杂性,但增强了对知识图谱中复杂关系的建模能力。
















 8853
8853

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








