PyTorch教程（十）：单层感知机以及梯度更新

单层感知机模型

$$\begin{gathered} y=XW+b \\ y=\sum x_i\ast w_i+b \end{gathered}$$

单层感知机模型的每一个输入节点$x_i$和对应的权重$w_i$相乘累加后，与bias相加，便得到了预测值。

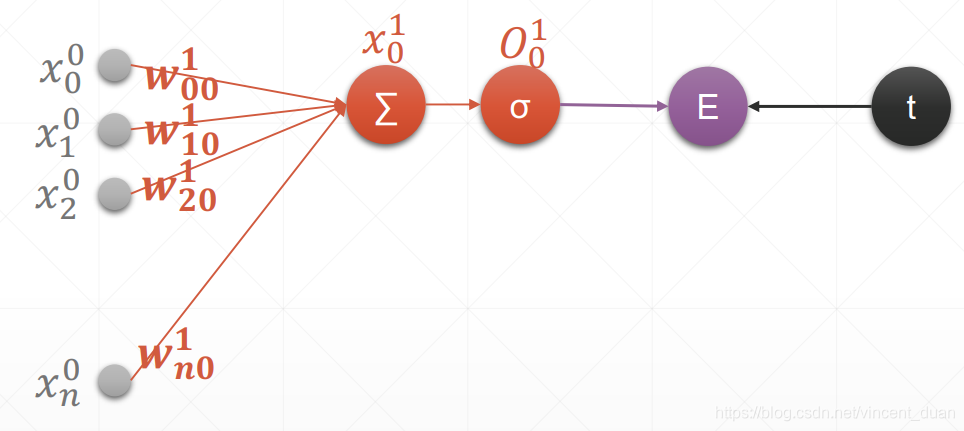
我们使用sigmoid函数作为激活函数，通常使用符号$\sigma$表示。
对于最左边的输入层的上标，也就是$x_n^0$中的0表示第0层，n表示第0层第n个元素节点。

从$w$到$\sigma$是1层，$w_{ij}^1$表示第1层,i表示连接的上一层$x_i$，j表示本层的第j个节点。因为上图中只有一层，所以j=0 。$x_0^1$中1表示第一层，0表示第一层的0号节点【这里讨论单层输出感知机，所以第一层只有一个节点】。$x_0^1$经过激活函数之后，有一个输出值$O_0^1$，其中1表示第一层，0表示第0号节点。

随后，$O_0^1$与target值计算：$Error（Loss）=\sum (O_0^1-target{)}^2$

梯度

Loss计算公式：
$$E=\frac{1}{2}(O_0^1-t{)}^2$$
这里引入了一个额外的$\frac{1}{2}$是为了与求导后的数2抵消掉。不会影响单调性的。
$$\begin{gathered} \frac{\partial E}{\partial w_{j0}}=(O_0-t)\ast \frac{O_0}{\partial w_{j0}} \\ \frac{\partial E}{\partial w_{j0}}=(O_0-t)\frac{\sigma (x_0^1)}{\partial w_{j0}} \\ \frac{\partial E}{\partial w_{j0}}=(O_0-t)\sigma (x_0)(1-\sigma (x_0))\frac{\partial x_0^1}{\partial w_{j0}} \end{gathered}$$
求导之前需要先向右计算一次所有的变量值，这就是向前传播
$$\frac{\partial x_0}{\partial w_{j0}}=\frac{\partial \sum w_{j0}{x}_j^0}{\partial w_{j0}}=x_j^0$$
因此上面的公式得到最终结果：
$$\frac{\partial E}{\partial w_{j0}}=(O_0-t))O_0(1-O_0)x_j^0$$

方法实现

输入10个特征的x

x = torch.randn(1,10)
# tensor([[ 0.5817, -1.1089, -0.9756, -0.4556, -0.2144, -1.1662,  1.9232,  0.2331,
#         -1.2987, -0.4950]])
w = torch.randn(1,10,requires_grad = True)
# tensor([[-1.0490, -1.7553,  0.1665, -0.0458, -0.8664, -0.3328, -0.1398,  1.2416,
#          1.3097, -0.4996]], requires_grad=True)
o = torch.sigmoid(x@w.t())
# tensor([[0.5831]], grad_fn=<SigmoidBackward>)
loss = F.mse_loss(torch.ones(1,1),o)
# tensor(0.1738, grad_fn=<MseLossBackward>)
loss.backward()
w.grad
# tensor([[-0.1179,  0.2248,  0.1977,  0.0923,  0.0435,  0.2364, -0.3898, -0.0472,
#          0.2632,  0.1003]])

这样就得到了每一个$w$的梯度，随后可以根据$w^{\prime }=w-0.001\ast \nabla w$来更新参数了。