【三角】和差角公式的证明与积化和差和差化积公式的推导

基础三角公式

单位圆

所需基本三角公式：

sin(a) = -sin(-a) 

cos(a) = cos(-a)

 

正切与正弦/余弦的和/差角公式的证明

 

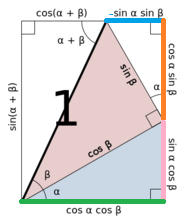
由右图可知 sin(a+b) 和 cos(a+b) 公式，将 b 用 -b 替换即可得差角公式

由左图可知 tan(a+b) 的公式，将b用-b替换即可得差角公式。由 cot = 1/tan 可得余切的和差角公式

 

和差化积公式的证明

基于和差角公式得如下四组等式

cos(a+b) - cos(a-b) = cos(b)cos(a) - sin(b)sin(a) - [cos(b)cos(a) + sin(b)sin(a)] = -2sin(b)sin(a)

cos(a+b) + cos(a-b) = cos(b)cos(a) - sin(b)sin(a) + cos(b)cos(a) + sin(b)sin(a) = 2cos(b)cos(a)

sin(a+b) - sin(a+b) = cos(b)sin(a) + sin(b)cos(a) - [cos(b)sin(a) - sin(b)cos(a)] = 2sin(b)cos(a)

sin(a+b) + sin(a+b) = cos(b)sin(a) + sin(b)cos(a) +  cos(b)sin(a) - sin(b)cos(a) = 2cos(b)sin(a)

 

PS：只需记忆一条边，再进行公式推理乘上系数2即可：

记忆图片

 

PS：应用时如给 cos(100)-cos(50) 列一个二元方程，需要自己得出 a与b 是多少

  可解得  

 

 

积化和差公式证明

基于和差化积公式得如下四组等式

sin(a)sin(b) = -[ cos(a+b) - cos(a-b) ]/2

cos(b)cos(a) = [ cos(a+b) + cos(a-b) ]/2

sin(b)cos(a) = [ sin(a+b) - sin(a-b) ]/2

cos(b)sin(a) = [sin(a+b) + sin(a+b)]/2

 

注：两幅和差角证明的几何插图来源于网络