数值优化（四）——修正阻尼牛顿法

目录

线搜索最速梯度的困难

 经典牛顿法

修正阻尼牛顿法

必要性

如何构建修正矩阵M

 Cholesky分解

---

 

线搜索最速梯度的困难

数值优化（三）——线搜索最速梯度下降

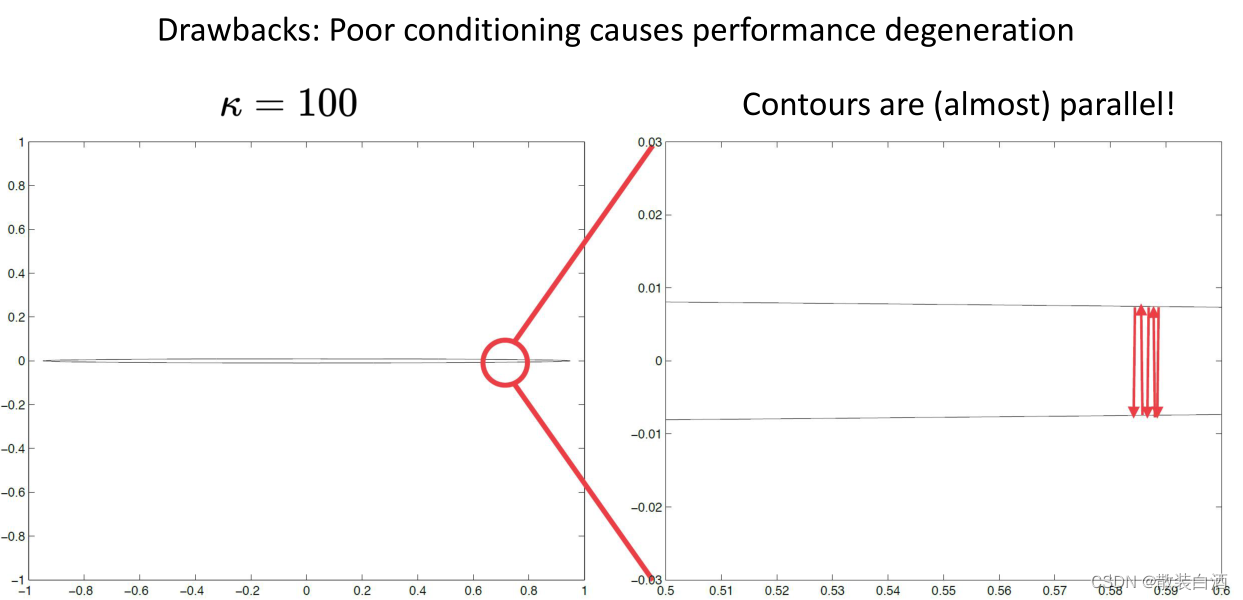
        对于光滑函数，当函数的曲率很大时，最速梯度下降的效果很差。因为最速梯度下降法只利用了函数的一阶信息即梯度，而曲率或条件数是二阶信息。因此，如果函数足够光滑，我们可以利用二阶信息改进下降方向，以加速算法迭代。

 经典牛顿法

        牛顿法其实际表现比梯度法要好，但该方法对函数的要求较高，需要二阶连续可微。牛顿法的基本思想是用迭代点的梯度信息和二阶导数对目标函数进行二次函数逼近，然后把二次函数的极小值作为新的迭代点，并不断重复这一过程，直到求出极小值。

        首先考虑一维情况，若给定初始值x，则可以构造如下的迭代格式：

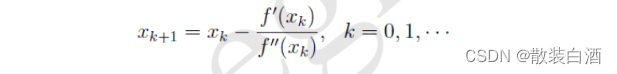
         下面考虑多维情况（N>1），对于二阶连续可微函数，考虑函数在迭代点处二阶泰勒展开：

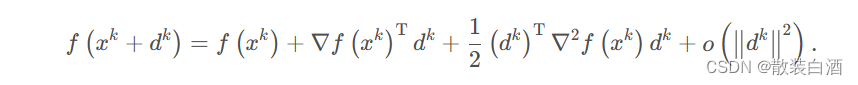
         忽略上式的高阶项，并将等式的右边看成关于d的函数求其稳定点（驻点），可以得到：

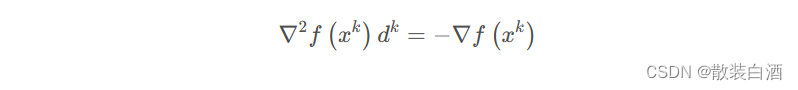
        当Hessian矩阵非奇异时，经典牛顿法的迭代格式如下:

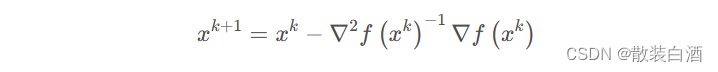
         由上式可知，迭代步长恒为1，即不用额外考虑步长的选取，也称该方法为经典牛顿法。

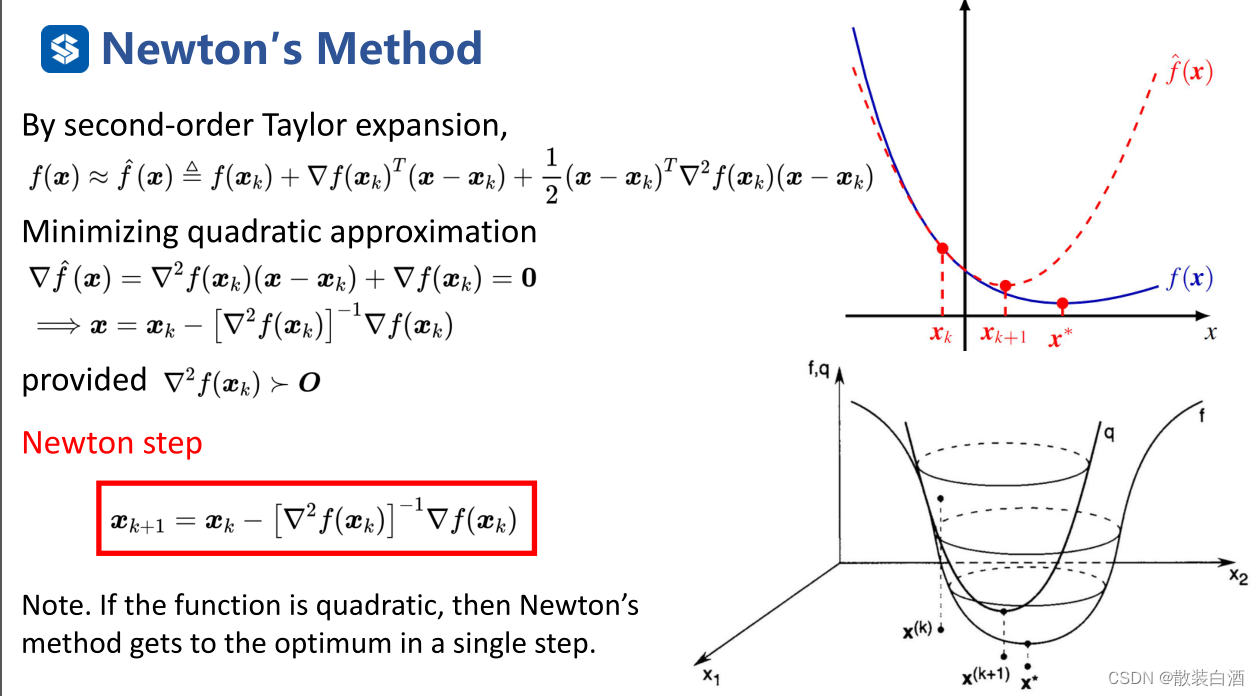
         经典牛顿法是收敛速度很快的算法，尤其是当目标函数为二次函数时，由于二次泰勒展开函数与原目标函数不是近似而是完全相同的二次式，Hessian矩阵退化成一个常数矩阵，只需要一步迭代就可以达到极小值点，但收敛性是有条件的：

        （一）初值敏感，即初值必须距离问题的解充分近，当初值距离问题的解较远时，经典牛顿法多数情况下失败。因此，实际情况下经常先用梯度类算法求得较低精度的解，然后再用牛顿加速获得高精度解。

        （二）Hessian矩阵需要为正定矩阵，非正定条件下可能迭代发散。收敛的前提是算法的搜索方向得让函数下降，搜索方向一定与负梯度方向之间的夹角为锐角。

        （三）条件数很大时，对初值要求会更高。

修正阻尼牛顿法

必要性

综上，经典牛顿法缺陷如下：

（1）每一步迭代都需要求解一个n维线性方程组，计算量大，Hessian矩阵极不容易计算也不容易存储；

（2）Hessian矩阵奇异或非正定，经典牛顿可能会发散；

（3）当迭代点距离较远时，步长=1会使迭代不稳定，有些情况甚至发散。

因此，从下面三方面考虑修正阻尼牛顿法：

 （一）构造一个严格正定（所有特征值大于0）的矩阵M，使其尽可能接近Hessian矩阵，且条件数较低；

（二）通过解线性方程组求出d，而不是通过求逆运算；

（三）用线搜索确定步长来增加算法稳定性（阻尼法）。

如何构建修正矩阵M

1、当函数为凸函数时，此时Hessian矩阵肯定为半正定矩阵，可采用如下方法构造M:

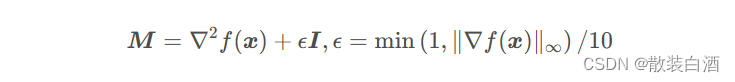
2、当函数为非凸函数时，Hessian矩阵为对称不定矩阵，则可采用Bunch-Kaufman分解与块对角线修正。

 Cholesky分解

设A对称正定，则存在唯一的对角线元素为正的下三角矩阵L，使得：

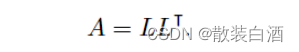
 该分解称为Cholesy分解。