史上最易懂的最小二乘法实践：线性最小二乘法推导与Python求解编程教程

最小二乘法有什么用？一般用它做什么事？

我们最早接触最小二乘法是在高中的时候学的。最小二乘法一般被用来拟合数据。什么叫做拟合数据？
就是给定你一堆数据，然后你假设这些数据是满足某种函数的，比如你假设这些数据是一条直线。现在问题来了到底这些数据所对应的那条直线斜率是多少截距是多少？这就得用最小二乘法来求解。
总结：最小二乘法拟合数据的步骤有两步。1.首先，假设这些数据符合某种函数。而这种函数往往有几个待设定的参数，不同数据对应不同参数。（就像直线一样不同数据，拟合这些数据的直线的斜率和截距都不一样）。2.然后，使用最小二乘法求解前面步骤提到的那几个待设定参数。具体怎么求解请看后面的内容。

从实例中学习线性最小二乘法

假设我们需要拟合下面这三个点。

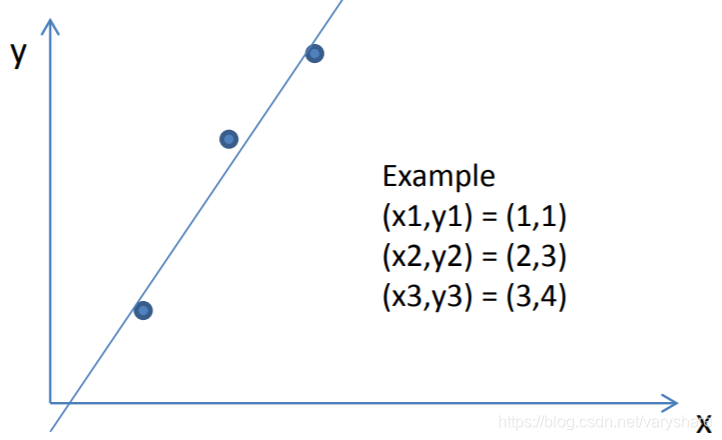
前面提到了第一步我们需要假设这些数据符合某种函数。在这里我们假设它们是符合线性函数的。假设拟合他们的直线方程为$y=kx+b$。其中k是斜率，b是截距。这两个都是未知的待求解的量
如果他们完全是在直线上那么他们应该要满足$y=kx+b$。现在有三个数据点那么代入到$(kx+b)=y$可以得到三个式子（由于数据并不完全在直线上所以是约等于）。
$$\begin{gathered} (kx1+b)\approx y1 \\ (kx2+b)\approx y2 \\ (kx3+b)\approx \end{gathered}$$