1. Camera坐标系->Pixel坐标系
xoy为相机坐标系,uv为像素坐标系。
Xc,Yc,Zc为为相机坐标系的点,u,v为像素坐标系的点。其关系为: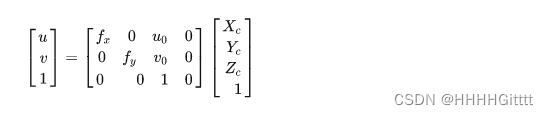
即:相机坐标系的点通过相机内参矩阵得到像素坐标系中对应的点
 文章讲述了在图像处理中,如何将相机坐标系(Xc,Yc,Zc)中的点通过相机内参矩阵转换到像素坐标系(u,v)的过程,强调了这一转换在计算机视觉和图像理解中的重要性。
文章讲述了在图像处理中,如何将相机坐标系(Xc,Yc,Zc)中的点通过相机内参矩阵转换到像素坐标系(u,v)的过程,强调了这一转换在计算机视觉和图像理解中的重要性。
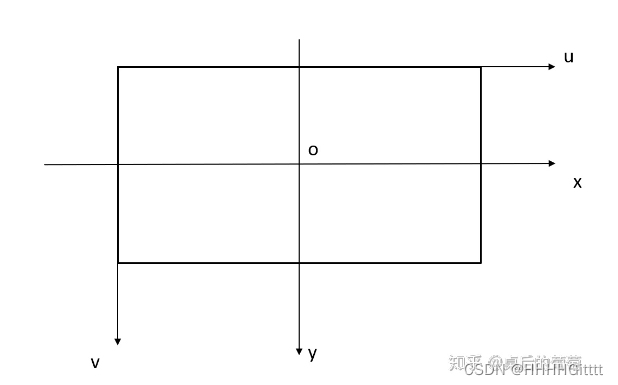
xoy为相机坐标系,uv为像素坐标系。
Xc,Yc,Zc为为相机坐标系的点,u,v为像素坐标系的点。其关系为: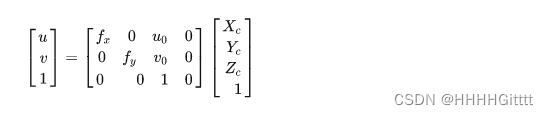
即:相机坐标系的点通过相机内参矩阵得到像素坐标系中对应的点
您可能感兴趣的与本文相关的镜像

PyTorch 2.6
PyTorch 是一个开源的 Python 机器学习库,基于 Torch 库,底层由 C++ 实现,应用于人工智能领域,如计算机视觉和自然语言处理
 6062
6062

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


