mini-batch梯度下降
在大数据等数据量大的时候,使用深度学习会导致很长的计算时间。故我们引用了一些优化算法,提高算法运行效率。
mini-batch梯度下降将数据集分为t个子集。每一个子集分别进行梯度下降。


理解mini-batch梯度下降
batch梯度下降的图像如图左图所示,mini-batch梯度下降的图像如图右图所示
可见mini-batch梯度下降的曲线并非光滑下降的。因为不同的小数据子集,其计算花费不一定为最小。可能由于极端数据,导致某一子集中,计算花费变大。但是总体趋势,却是下降的。

如何选择mini-batch子集的大小
如果mini-batch size=m,即整个数据集是一个整体的大向量-batch 梯度下降
如果mini-batch size=1,即每个数据都是独立,独立进行梯度下降-stochastic随机梯度下降
batch梯度下降缺点:
每一轮迭代过程的计算时间过长(因为要遍历整个数据集),且占用大量内存
stochastic随机梯度下降缺点:
总体的运行时间过长
mini-batch介于两种算法之间

如何选择你的mini-batch的大小
假如数据量小于2000,使用batch梯度下降
大于2000,使用mini-batch。且mini-batch size最好是2的次方数,已满足内存的空间。
注意,使用mini-batch时一定要注意不要超过cpu/gpu的存储空间

mini-batch算法补充介绍:
训练中的另一个重要概念是epoch。每学一遍数据集,就称为1个epoch。
举例:
若数据集中有1000个样本,批大小为10,那么将全部样本训练1遍后,网络会被调整1000/10=100次。但这并不意味着网络已达到最优,我们可重复这个过程,让网络再学1遍、2遍、3遍数据集。
注意每一个epoch都需打乱数据的顺序,以使网络受到的调整更具有多样性。同时,我们会不断监督网络的训练效果。通常情况下,网络的性能提高速度会越来越慢,在几十到几百个epoch后网络的性能会趋于稳定,即性能基本不再提高。
指数加权平均数
加权平均的值:
vt = β vt-1 + (1 - β)θt
θt为实际的每天温度
vt为加权平均的值
β为参数

我们计算指数加权平均数为综合了几天的平均值。可以采用1/1-β 计算。
例如:
β=0.9时,1/1-β =10,相当于综合了10天的平均数。曲线更平缓。
β=0.5时,1/1-β =2,相当于综合了2天的平均数.曲线上下波动更大。

指数加权平均的偏差修正
我们知道指数加权平均相当于综合几天的平均值,那么初期第一天,第二天,前面是没有数据的。就无法达到综合几天的理念。故原来的公式,会产生初期阶段曲线值很低(紫色的线)。
为了克服这种情况,我们修改了公式为:
加权平均的值 = vt / 1 - βt
由此初期变成了β t,vt除以一个很小的数,会让初期的值大一些。防止紫色线的情况

动量梯度下降法Momentum gradient descent
我们可以看到传统的优化函数,梯度下降方法。其运行过程中,会产生很多的来回摇摆的震动,导致计算时间大大增加(如蓝色的线)。但是我们增加梯度下降的学习率的话,想要加快算法运行的时间。会导致更大的震动,最后可能无法收敛到最优值。
故我们引入了新的优化函数,动量梯度下降法。其类似于计算梯度下降的指数加权平均数。故得出的曲线将更光滑。能够节省大量的计算时间,即可达到最优值。
计算公式:vθ = β vθ + (1 - β)θt

有的书上会忽略,公式中的(1 - β)。相当于vdw缩小了1 / 1 - β 倍。则学习率α 也要改变1 / 1 - β倍。这两种方法,都类似效果。区别在于学习率α。但是缺点在于,当你调整β参数时,同时可能还要修改学习率α。

RMSprop(root mean square prop)算法
另一种优化方法,采用RMSprop算法。我们可以看到我们要尽可能增大水平方向的迭代速度,减慢竖直方向的震动幅度。
故我们要减小Sdw,增大Sdb。我们在w = w - α dW / √Sdw + ε ,尽可能除以一个小的数,会导致w变大。来增加函数在水平方向的速度。
我们在b = b - α db / √Sdb + ε ,尽可能除以一个大的数,会导致b变小。来减小函数在竖直方向的震动。
本身根据原来梯度下降的函数图像,就是b方向震动幅度大,w方向幅度小。也就是本来梯度下降,b的导数db大,w的导数dw小。所以,RMSprop正是利用此点,除以大的会变小,除以小的会变大,达到目的。
注意:
1.公式中的 dw2 与 db2 都是element-wise的平方。 直觉来说,我们希望(1 - β)乘一个更大的dw 与 db来让加权平均的值更大。就能让曲线更平滑,消除震动。所以采用dw平方,db平方。(参见标题:指数加权平均的偏差修正)
2.我们还需要注意w = w - α dW / √Sdw ,中的√Sdw不接近0,这样会导致w的值异常大。故我们增加了ε ,一般ε=10-8,来防止除以很小的数这种情况的发生。

Adam优化算法
RMSprop算法与Adam算法,被证明为适用于不同结构的深度学习网络中。其中Adam算法由Momentum梯度下降法 与 RMSprop算法组合而成。
公式中Momentum梯度下降法的Vdw,RMSprop算法的Sdw 都加入了偏差修正。
即:
Vdw / ( 1 - β1t )
Sdw / ( 1 - β2t )
最后的w,b更新采用了,修正后的vdw 除 根号 修正后的sdw+ε


Adam算法的参数选择:
其中
学习率α需要被调整
β1一般默认采用0.9
β2一般默认采用0.999
ε一般默认采用10^-8

学习率衰减
如果我们固定单一一个学习率不变,我们可以看到,由于采用mini-batch梯度下降法。每一个不同的batch之间,会产生噪音,影响整体结果。故最后会无法收敛,且与最优值在一个大的区间范围内震荡。
为了解决这种问题,我们采用学习率越来越小。即最后曲线,会在一个小区间震荡。十分接近最优值。

注意公式中,1 epoch代表一次遍历整个数据集。

学习率衰减还有不同的方法,如:
指数衰减 (exponentially decay),常数k除以根号epoch,离散衰减,
或者有的人手动来减小学习率(如果数据量不大的话)

局部最优问题
我们原来经常讨论,局部最优问题。即梯度下降会被困在局部低点,无法达到全局最优值,一般出现在二维函数中。但是对于特征数多,出现的高维空间。我们一般会产生saddle point(鞍点),而不是卡在局部最优值。(某一方向是凸函数,某一方向是凹函数)
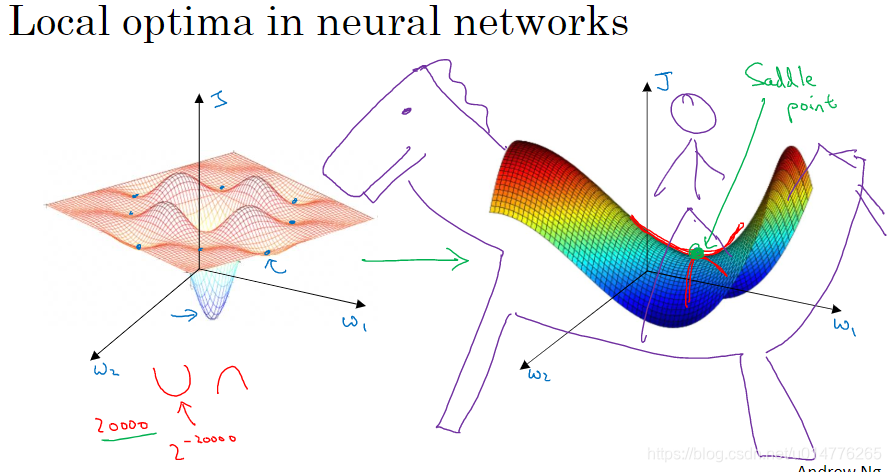
如果产生鞍点,会导致某一方向梯度接近0,其这一段下降速度会很慢。所以我们采用优化的梯度下降,Adam,RMSprop算法来避免这些问题。








 本文深入探讨深度学习中的优化算法,包括mini-batch梯度下降、动量梯度下降法(Momentum)、RMSprop算法及Adam优化算法。解析各种算法的工作原理,及其在大数据集上的应用优势。同时,介绍了学习率衰减策略,以及如何解决局部最优问题。
本文深入探讨深度学习中的优化算法,包括mini-batch梯度下降、动量梯度下降法(Momentum)、RMSprop算法及Adam优化算法。解析各种算法的工作原理,及其在大数据集上的应用优势。同时,介绍了学习率衰减策略,以及如何解决局部最优问题。
















 645
645

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








