吴恩达deeplearning.ai《改善深层神经网络：超参数调试、正则化以及优化》-深度学习的实用层面（一）

训练/开发/测试集

数据集划分：training set,dev set (cross validation set)，test set
一般会按照比例划分，但是对于大数据来说。如果有1000 000的数据。我们会缩小dev set和test set的大小。因为这两个数据集，是用来选择合适的算法，与评估算法的各项指标的。故，本案例中，采取了10 000，即1%的比例

另一个问题：训练集数据，测试集数据来源不匹配

产生原因：

我们从网上收集了大量的猫的图片来训练。
但是我们的验证集，测试集图片的来源是来自 app中用户上传的图片。这些图片由用户拍照，可能模糊，或者分辨率不高。且数量很少。
故此时，我们要保证验证集，测试集来源于同一个分布。（如果我们没有test set，只有dev set来替换test set的评估功能，同时dev set还有原来的算法选择功能，也是可以的）

偏差与方差

如果train set 的错误率很高，dev set的错误率很高，且两者接近。则为 high bias（欠拟合）的情况。
如果train set的错误率很高，且dev set的错误率更高。则为high bias 和 high variance的情况（欠拟合与过拟合同时存在）
我们使用贝叶斯错误率来评估，训练集与测试集上的错误率是否高。如果贝叶斯错误率为15%，那么训练集上错误率为15%，则不算欠拟合。

过拟合与欠拟合同时存在的情况如下图。

在二维空间其可能不好理解。但是在更高维参数空间，更可能出现，某一个区域欠拟合，某一个区域过拟合。

机器学习基础

假如神经网络high bias，我们就需要更大的网络或者训练时间更长（不一定产生效果），更合适的神经网络模型

假如神经网络high variance，我们就需要更多的数据量，或者使用正则化来减少high variance，更合适的神经网络模型

深度学习优点：

不需要过多关注，bias 和 variance中的平衡问题。即：bias改变的时候，可能影响variance也会同时改变。而深度学习，在使用上述方法时，对于对方的影响较小

正则化

这里我们解释一下吴恩达视频中说的，L2正则化：w的欧几里得范数平方
经过搜素，其实就是我们线性代数中说的向量的模，也叫作L2范数

注意：L2正则化为L2范数的平方，故不需要开平方。为所有元素的平方和。上图为引用。助于理解。

L1范数

L1范数是指向量中各个元素绝对值之和。
使用L1正则化，会是参数W变得稀疏（参数中有很多0）

对于b的正则化，我们一般可以忽略。因为W参数是nx维的向量，里面包含了nx个参数。而b参数，只是单一一个数。其单个数对于整体正则化的影响是很小的。故，b参数的正则化一般是可以忽略的。

总结：目前人们更倾向于多用L2正则化。

对于矩阵范数（也叫作平方范数）W^[l]:表示W矩阵中，所有元素的平方和。（n^[L],n^[L-1]）.其中n【l-1】表示隐藏单元的数量。n【l】表示l层单元的数量
在线性代数中，||x||的形式称作：弗洛贝尼乌斯范数 （吴恩达：一些原因，它不叫做L2范数。但是意思基本相同）

L2正则化（L2 regularization）有时也被叫做：权重衰减（weight decay）

原因：

将公式展开，W^[L]提出来。其相当于系数（1-αλ/m） ，这个系数小于1.故类似于梯度下降，W^[L]的系数在一轮轮的递减

为什么正则化可以减少过拟合

因为如果正则化系数λ，足够大。就会导致系数W^[L]越来越小。相当于使用正则化，使神经网络中的隐藏单元的效果越来越小。

因为如果正则化系数λ，足够大。就会导致系数W^[L]越来越小。以tanh激活函数举例，系数z^[L]就会越来越小。我们观察tanh激活函数图像可以看出，在中间一段区间，函数图像基本可以看做为线性的。也就是导致整个参数z^[L]越来越线性。越线性也会导致，神经网络更容易high bias。

注意：

我们使用梯度下降做优化算法时，在损失函数中要加上正则化项。因为梯度下降必须保证其是单调下降的。前面的项∑ L(y⁽ⁱ⁾ , y⁽ⁱ⁾ ) 并不能保证其是单调下降的，故增加单调下降的正则化项，才能保证整个损失函数为单调下降的

dropout正则化

思路:

给每一层隐含层设置概率。如给每一层设置0.5的概率，则会随机删除掉一些节点。并且删除与节点连接的线。



inverted dropout
keep-prob为节点保留的概率
np.multiply(a3,d3) 是element wise，对应元素相乘

注意：

此处a3=a3/keep-prob
因为a3由于dropout减少了20%，为了弥补a3减少的损失。赋值时，a3=a3/keep-prob（相当于除以0.8）.这样期望值不会影响，即不影响z4。
早期的dropout没有除keep-prob，导致了在测试阶段其期望值混乱

keep-prob越接近1，表示节点的保留越多。drop-out算法主要运用在机器视觉领域（其输入图片的特征数庞大，且训练的图片数量很少）所以采用drop-out防止过拟合。

此外，drop-out算法可以对输入层设定参数，其x1，x2，x3输入层的参数，一般设定接近于1。

其他正则化方法

数据加强

如果训练数据不够时，我们可以对图片数据采用翻转，裁剪。对数字数据采用形变等方法扩大数据量，防止过拟合。

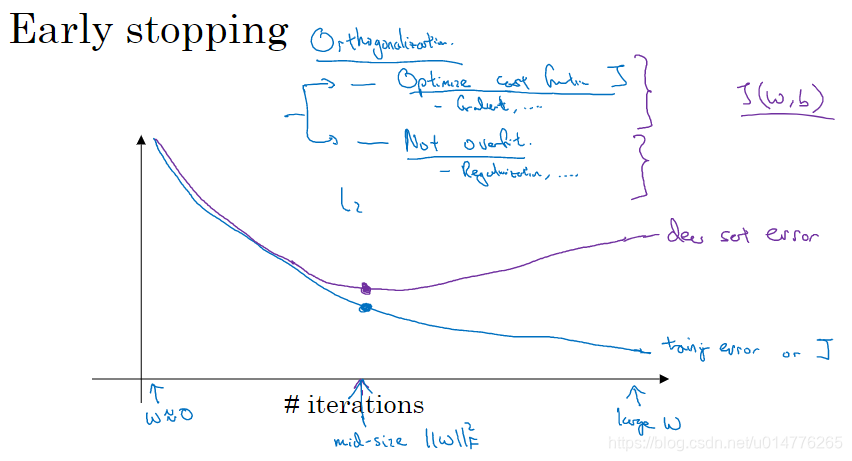
early stopping

我们会发现验证集的错误率会先下降，再上升。故，选用验证集曲线最低点的参数是最佳的。我们可以使用early stopping算法，跑一次即可选出参数。
或者采用L2正则化，但是需要手动调整λ的值。

正则化输入

我们使用subtract mean方法，将数据的平均值归一为0。
之后我们使用normalize variance方法，除以x2轴方向方差，使数据在x2轴方向做到与x1轴的尺度基本相同。

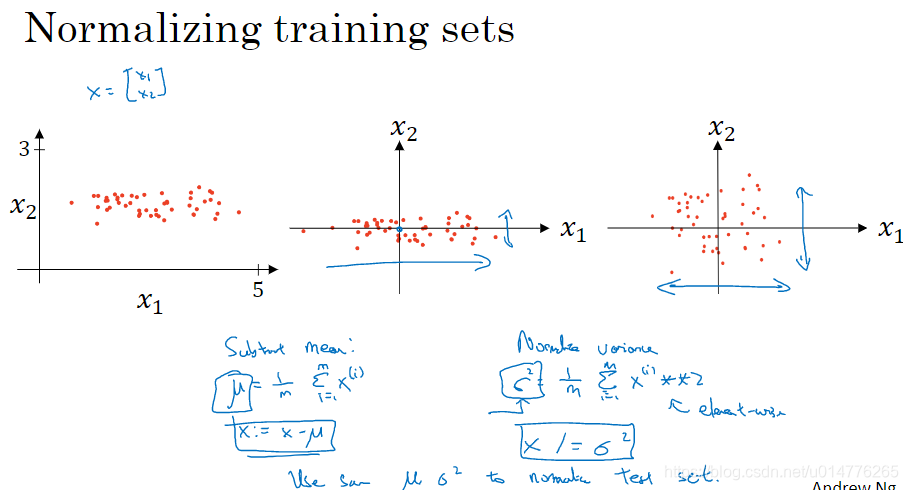
当我们的不同数据特征，范围相差较大时，建议使用归一化操作。

即：

x1的范围[1,1000]
x2的范围[0，1]
此时如果采用梯度下降，其在椭球体的长边上为起点，想要下降到椭球体的最低点。其需要很长时间的路程（梯度下降消耗更多时间）。故采用归一化，将特征归一成一个尺度。使用梯度下降时，其图形更接近半球体。即任何位置为起点，所走的路程都最短，节约梯度下降的计算时间

梯度消失与梯度爆炸

假设我们有一个层数很多的神经网络，其采用线性激活函数。且经过训练其b向量为0.
则，我们可以得到y^ = w^[L] w^[L-1] `````````w^[2] w^[1] x
若w向量中每个w^[i] 的值都为 1/2。则可以计算出每个节点的值为 1/2 ,1/4,1/8······由此可见，若w^[i]的值小于1，经过多层的神经网络计算。其最后的激活函数的值，会呈指数式下降。产生了梯度消失。即过于小，采用梯度下降其每次下降步长很小，大大增加梯度下降计算时间。
同理，若w^[i]的值都大于1。其节点值会指数式上升。产生梯度爆炸，同样大大增加梯度下降的计算时间。

神经网络的权值初始化

我们可以看到当输入的节点越多时（n越大时），会导致z越大。所以为了防止节点值越来越大，我们需要w的导数在[0,1]区间增长快，[1,+∞]区间增长慢。故，选用2/n为w的导数。

则反推，w^[L]为np.sqrt(2/n^[L-1])故第L层权重的计算公式w^[L]如下：

注：

经过验证证明，如果使用ReLU激活函数，采用2/n^[L-1]，其效果更好。
如果使用tanh激活函数，1/n^[L-1]效果更好。也可使用2/n^[L-1]+n^[L]

梯度的数值逼近

在实施反向传播时，有时我们不知道导数g(θ)是否计算正确。故我们需要一种方法来检验。所以我们就提出了双边误差的方法来检验导数。原理基本上就是导数的高数定义，如上图。

梯度检验

检验反向传播时导数计算的正确性。将各个向量 w^[1],b^[1]…w^[L],b^[L]作成一个大向量θ，将dw^[1],db^[1]…dw^[L],db^[L]形成一个大向量dθ。其θ与dθ维度相同。

检查dθappear与dθ之间的欧几里得范数（向量距离，即差平方开根号），若与ε数量级相当，则是正确的。若远远大于ε数量级，则梯度求解错误

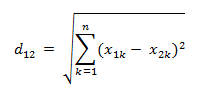
梯度检验的注意事项

1.在训练中不要运用，只在debug中使用。
训练中需要多轮迭代，使用梯度检查会导致每一轮都要计算。及其占用计算资源

2.假如梯度检查失败了，要回去看看哪里有bug。
比如：db^[L]差距很大，dw^[L]差距很小。那么很可能反向传播db求解过程中，出现了bug

3.记住求梯度时，正则项也要算在内

4.使用dropout算法时，不要同时使用梯度检查。应当暂停dropout，之后开始梯度检查

5.先使用随机初始化w，b参数后，训练后，再运行梯度检查
如果初始化w，b为0.那么运行梯度检查一定是正确的。但是如果w，b不是0，那么有可能产生梯度检查错误