deeplearning笔记2：改善深层神经网络

train/dev(cross-validation)/test set设定

• in smaller datasets like 100, 1000, 10000，the proportion of every part is 70%/30%，or 60%/20%/20%.
• in large datasets like 1 million data or more，the proportion of every part like：98%/1%/1%，or 99.5%/0.25%/0.25%，99.5%/0.4%/0.1%.
• note that ：dev set should have same distribution of test set。比如：如果你的train data为网络中猫的照片，而test data为手机拍摄的猫的照片，则至少应该保证你的dev data也为手机拍摄的猫的照片。
• 由于dev set已经承担了validation的责任，所以没有test set也是可以的。

model bias 和 variance的分析

• bias 过低时，可能导致大的variance，如图（3）；适当增加bias，可以降低variance，如图（1）
  

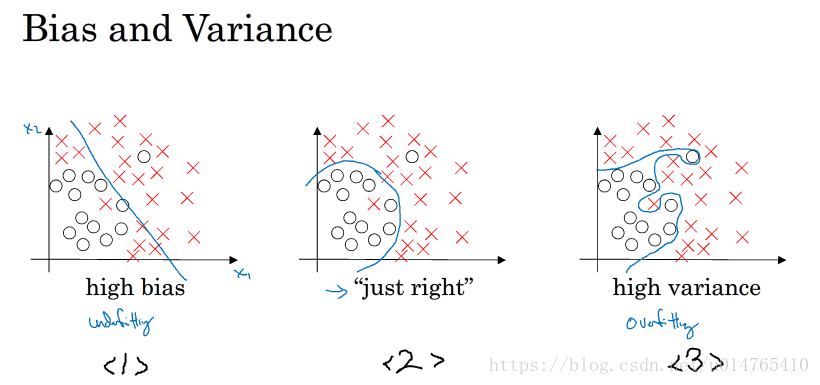
• model也可能出现这种情况，同时拥有高bias和高variance。如下图所示：
  
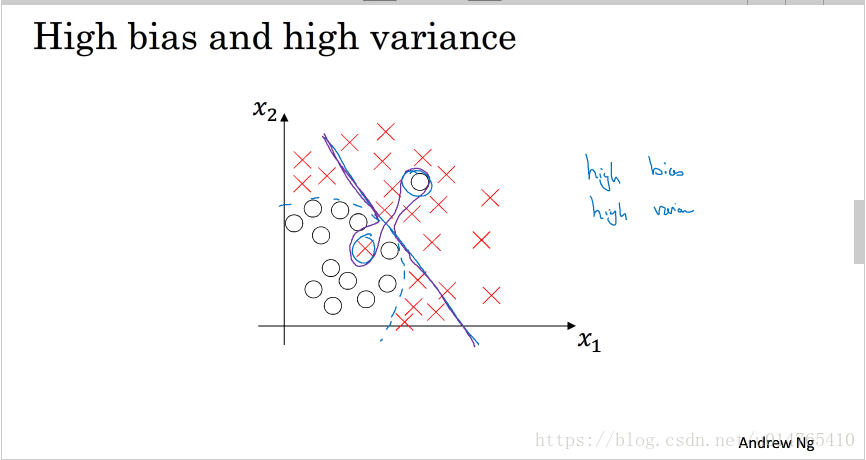
  在实际应用中，我们可以通过检测model 的bias和variance情况，来决定采用何种方法提高model的performance。如：当model有很高的bias时，我们可以通过：1）增加训练时间；2）训练一个bigger nerual network；3）调整神经网络的结构；等方法来降低bias。当model有很高的variance时，我们可以通过1）增加data set；2）正则化；3）调整神经网络结果；等方法降低variance。深层神经网络的一个最大优点是在调节bias时，不会伤害到variance，vice versa。

正则化

• logistic regression中正则化方式可以采用L1，或L2，其中通过L1正则化可以获得sparse weight which most of them equals 0。公式如下：
  
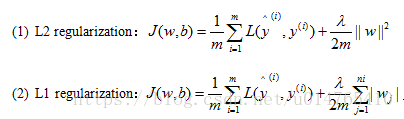
• 神经网络正则化公式如下：
  
  
• dropout regularizaiton
  以下面的3层神经网络为例，介绍dropout regularization:
  
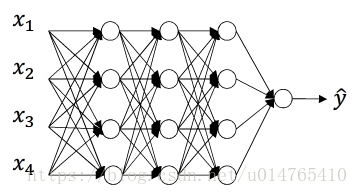
  以第3层网络的dropout为例说明：
  step1：自定义keep-probability；
  step2：给第3层hidden layer各个unit随机赋予一个probability：np.random.rand(a3.shape[0]，as.shape[1])，对于probability<keep-prabability的unit，将其remove。可以通过以下code实施：

import numpy as np
d3 = np.random.rand(as.shape[0],as.shape[1])<keep-prob  #d3为boolean value:{True:保留的unit,False:去掉的unit};
a3 = np.multply(a3,d3) #将hidden layer3中的各个unit根据keep-prob进行删减后，得到新的hidden layer3
a3 /= keep-prob #为了保证修改前后hidden layer3的期望值不变，将新的a3除以keep-prob，从而保证，z^[4]^（z^[4]^=w^[4]^a^[3]^+b^[4]^）值不变

note that：dropout只在training阶段实施：在进行forward propagation和backward propagation前，先实施dropout，然后在进行propagation。每一次iteration中，dropout的unit都是随机的（根据各个unit上的随机概率与keep-prob的大小，决定其去留）。
dropout相当于L2 regularizaiton，能够降低|w|²的值。他常被用于计算机视觉，在这个领域input vector维度很高，为了避免overfitting，需要对w进行正则化，从而降低模型的复杂度。
dropout regularization的一个缺点是：使用它之后，很难计算cost function，因而很难绘制costfunction-iteration图来进行debug，一个折中的办法是，首先关闭dropout，绘制costfunction-iteration图，查看costfunction是否降低，如果没有bug，则打开dropout；

• 其它的正则化方法
  
  
  

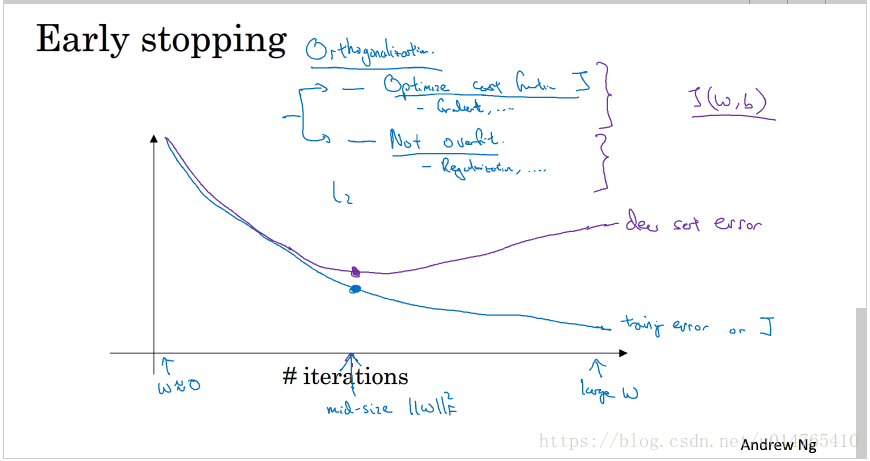
归一化输入

当你的trainingdata各个feature的scale不同时，你可以对trainingdata进行normalization(mean=0,variance=1)，这能加快gradient descent的收敛速度。需要注意的是：你的testdata需要用同样的normalization进行处理。
normalization并不会harm machine learning，所以，如果你不确定是否需要使用normalization，你可以always使用它。

梯度消失与梯度爆炸

When training deep neural network , exploding or vanishing gradient may happen ;Initializing your weight skillfully can effectly avoid this situation；

• 什么是梯度消失与梯度爆炸
  
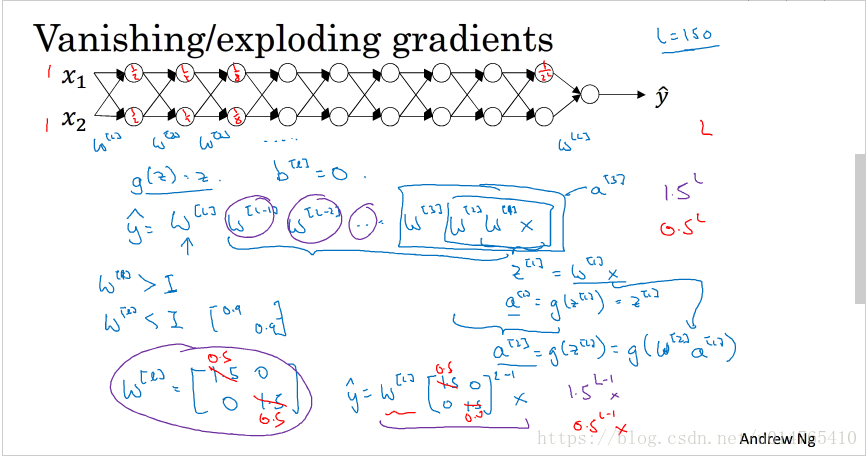
  以上图的神经网络为例说明：
  assuming that ：active function g(z)=z
  当各层的weight > 1时，则最后的output y=w^[L]w^[L-1]…w^[1] x，y将以w^L的方式增长，对应的gradient称为exploding gradient。
  当各层的weight < 1时，则y将以w^L的方式消减，对应的gradient称为vanishing gradient。
  无论是exploding or vanishing gradient，都会降低gradient descent的收敛速度，特别是当gradient与L呈指数级差别时，更是如此。以上问题可以通过合适的初始化weight，来解决。（L：hidden layer的层数）
• 神经网络weight的初始化
  
  为了降低exploding or vanishing gradient的影响，我们可以initialize weight to guarantee the variance of weight equals 1/n，namely, variance(w^[l])=1/n^[l-1],n^[l-1] denote the number of unit in layer l-1。
  为了达到上述目的，我们可以将weight初始化为：w^[l] = np.random.randn(shape) * np.sqrt(1/n^[l-1]) #注意使用randn可以保证variance of weight符合要求。
  If active function is ReLu：then : w^[L]=np.random.randn(shape)*np.sqrt(2/n^[L-1]);
  If active function is tanh ：then :w^[L]=np.random.randn(shape)*np.sqrt(1/n^[L-1]);sometimes,people use np.random.randn(shape)*np.sqrt(1/(n^[L-1]+n^[L]))
  w^[L] denote the weight of L layer;
  n^[L-1] denote the number of unit in L-1 layer；

通过gradient check formular来进行梯度检验

• gradient check formular
  
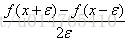
  我们可以利用上述公式，检验backward propagation中的dw计算是否正确，具体实现方式如下：
  gradient dw_approx的近似值采用公式：dwi=(J(w1,w2,…wi+theta,…)-J(w1,w2,…,wi-theta,…))/2*theta；（assuming ：theta=10^-7）
  检查 dw_approx与dw是否相等，如果：||dw_approx-dw||2/(||dw_approx||2+||dw||2)近似等于theta，则说明gradient计算正确；如果与theta相差好几个数量级，如10^-3，则说明dw计算有误。
  
• gradient checking tips
  gradient check只用于debug；
  如果检查出异常，则检查dw各个分量与gradient check formular的差异，进行debug；
  如果cost function有正则化项的话，则检测时，dw也要加上正则化项；
  dropout regularization不能用gradient checking；
  AndrowNg建议（只是偶尔使用）：在初始化weight后使用一次gradient checking；然后training 几轮后，当weight都远离了0时，在使用一次；

Mini-batch梯度下降中的一些注意事项

• in large datasets(millions dataset)：mini-batch GD do better than batch GD。
• mini-batch size的选择
  当dataset < 2000，可以直接用batch GD
  mini-batch size可以选择2的指数级，如：64,128,256,512等较为常见；
  mini-batch size要与CPU/GPU内存 相符合。
  可以将mini-batch size作为一个hyperparameter用cross-validation进行验证。

some algorithms better than standard gradient descent

在介绍其它算法前，首先了解一下指数加权平均：

指数加权平均

• 指数加权平均
  以days 和 temperature的关系来说明指数加权平均的定义：
  如下图所示，theta_i表示第i天的温度。vⁱ表示i天温度的加权平均（用来拟合第i天的温度）。
  令v⁰=0，则vⁱ=0.9 v^i-1 + 0.1 theta_i，用该公式拟合的第i天的温度vⁱ降低了当天温度theta_i的权值，且以一定权值加入了第i天以前的所有day的温度，这种方式得到的第i天的温度，稳定性更强，同时也能够极大的避免outlier的扰动。
  
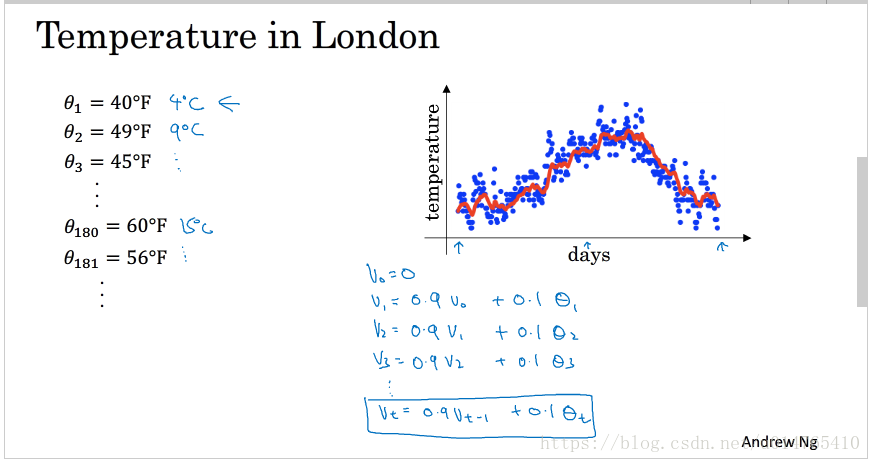
  将上述公式一般化：vⁱ=beta * v^i-1 + (1-beta) * theta_i，如下图所示：
  beta=0.9时，代表vⁱ为10天数据的加权平均；
  beta=0.98时，代表vⁱ为50天数据的加权平均；
  当beta取值较大时，说明vⁱ上第i天的数据比例较小，其对天数day的响应会相对滞后，day-temperature曲线相对平滑。当beta取值较小时，则vⁱ对day的响应很及时，但是，可能很容易受outlier的影响，day-temperature曲线非常的粗糙。
  
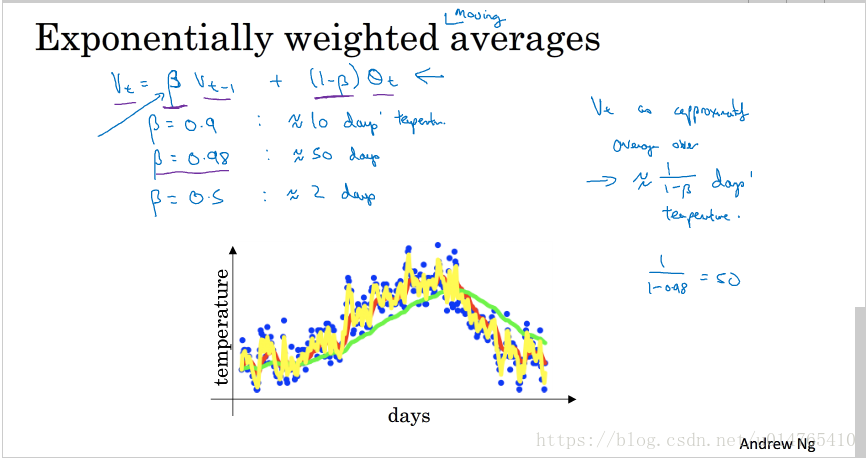
  下面解释“指数加权平均”的数学意义，以v¹⁰⁰为例：
  v¹⁰⁰ = 0.9 v⁹⁹ + 0.1 theta_100
  v¹⁰⁰=0.9(0.9v⁹⁸+0.1 theta_99) + 0.1 theta_100 = 0.1 theta_100 + 0.10.9 theta_99 + 0.9²v⁹⁸=0.1 theta_100 + 0.10.9 theta_99 + 0.10.9² theta_98 + 0.9³ v⁹⁷
  从上边的演算可以看出v¹⁰⁰实际上是theta_i vector与 0.1(0.9)^i-100 vector的乘积。值得一提的是，beta^1/(1-beta) 约等于 1/e，当betaⁿ的值过了1/e这个点后，其值会迅速下降。
• 指数加权平均的偏差修正
  原指数加权平均公式：vⁱ = beta v^i-1 + (1-beta) theta_i，该公式存在一个问题，即：由于设定v⁰=0，因此，在最初的拟合过程中，vⁱ偏小，随着时间的推移，该公式对temprature的拟合越来越好，如下图所示（绿色曲线为标准曲线，紫色曲线为该公式拟合的结果）：
  
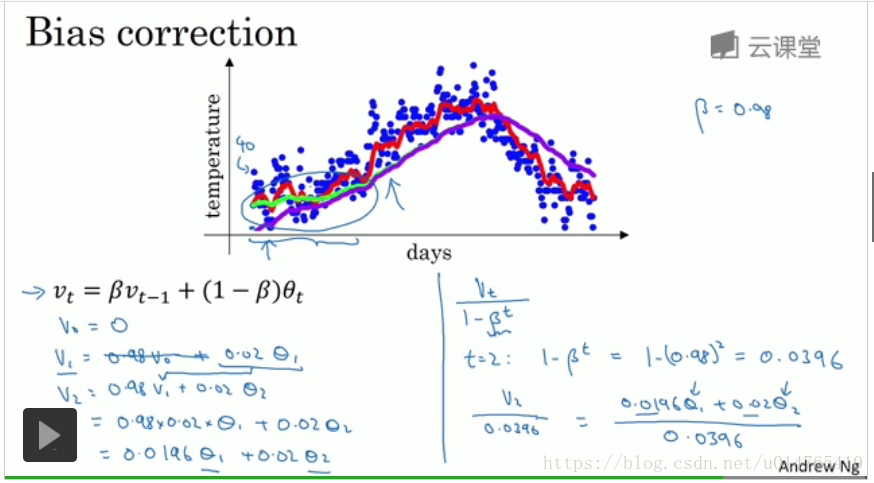
  为了解决上述的困境，在原公式的基础上，在加一个步骤：vⁱ = vⁱ/1-(beta)ⁱ，其中i为day。当i较小时，(beta)ⁱ的值较大，分母整体较小，此时可以增加原始vⁱ的值，而当i较大时，(beta)ⁱ的值较小，分母整体接近于1，此时vⁱ与原始的vⁱ相近。这种做法，在一定程度上解决了“指数加权平均”在最初的拟合过程中，数值偏小的问题。将改进方法总结如下：
  step1：ⁱ = beta v^i-1 + (1-beta) theta_i
  step2：vⁱ = vⁱ/1-(beta)ⁱ

动量梯度下降法(momentum)

动量梯度下降算法 核心思想：利用“指数加权平均”，计算dw，db，具体操作如下图所示：
初始化：v_dw=0，v_db=0
通过gradient descent计算：dw，db
v_dw := beta * v_dw + (1-beta) * dw
v_db := beta * v_db + (1-beta) * db
更新w,b：
w := w - alpha * v_dw
b := b - alpha * v_db
动量梯度算法在求w,b的更新步长时，除考虑当前迭代中的dw， db外，还考虑了前 1/(1-beta) 次的dw，db，从而alleviate the oscillation of weight, b，进而加快学习速度。
一般，beta=0.9时，算法运行效果较好。
note that：动量梯度算法 perform better than 标准梯度算法。

除上述介绍的动量梯度算法之外，还有一种“动量梯度算法”（如下图right-hand formular），他将dw,db上的系数（1-beta）去除，即：v_dw := beta * v_dw + dw，w := w - alpha * v_dw，这种改变相当于对v_dw做了1/(1-beta)的缩放，它使得alpha对beta的变化很敏感，因此，建议使用前述“动量梯度算法”。

RMSprop(root mean squaring prop)

RMSprop与momentum一样，可以减小在迭代过程中w,b的oscillation.
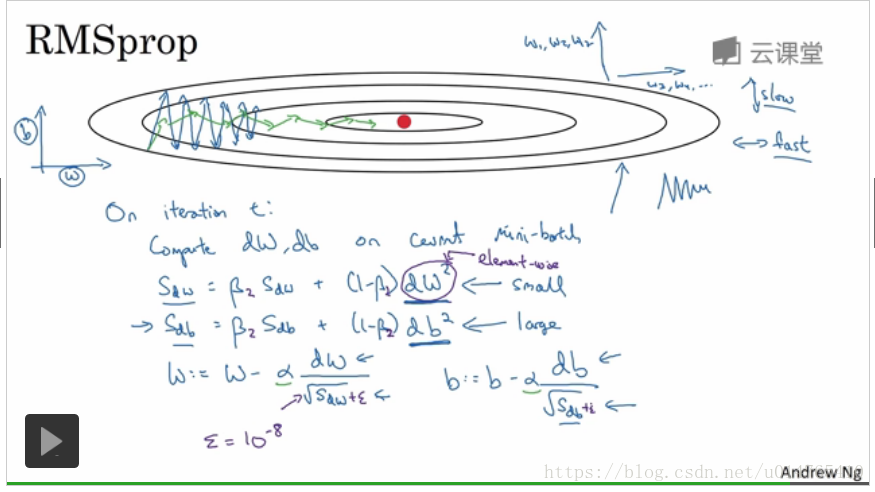
其具体定义如下图示：
初始化S_dw，S_db 为 0
利用gradient descent 计算 dw，db

为了防止由于S_dw或S_db = 0，而使更新步长过大，可在原更新步长的分母项上 加一个数值10^-8，如下图所示；
在RMSprop中，可以使用较大的learning rate。

Adam优化算法（adaptive moment estimation）

Adam优化算法结合了“momentum”和“RMSprop”两个算法，可加快neural network的学习速度，具体如下图所示：

在adam中，beta1，beta2，ekson常采用以下默认值，alpha需要进行选择，具体如下图示：

学习速率衰减

当各种gradient descent algorithm运行了一段时间后，w，b会比较接近其minimum，此时，如果还用以前的learning rate进行update的话，很可能错过w，b的minimum，因此，可以构建一个learning rate随着iteration进行而不断衰减的公式，从而使得learning rate适应w,b的变化，具体公式如下：

下图列了一些其他的learning rate衰减公式：
formular1: exponential decay：epoch.num：遍历trainingdata的次数
formular3: t:iteration的次数
formular4: discrete staircase：每到达一定的iteration次数，就更换一次alpha
formular5:如果你的learning model比较小的话，可以采用手动的方式调节alpha的大小，如：每几个小时，or几天手动调节一次。

local optima VS saddle point

如下图所示，在low dimenstional space，我们常会遇到“局部最优点”，这些point会影响 optimal algorithm的判断，使他们限于“局部最优点”，阻止他们向global optima迈进。而在high dimenstional space(>20000)，比起“局部最优点”，我们更常遇到的是“saddle point：gradient=0的点”，他会使optimal algorithm在很长的一段时间内进入一个平坦区，从而导致“w,b 更新缓慢，原地踏步”，而"momentum，RMSprop，Adam ”等算法均能有效克服saddle point的影响，加快algorithm学习进程。

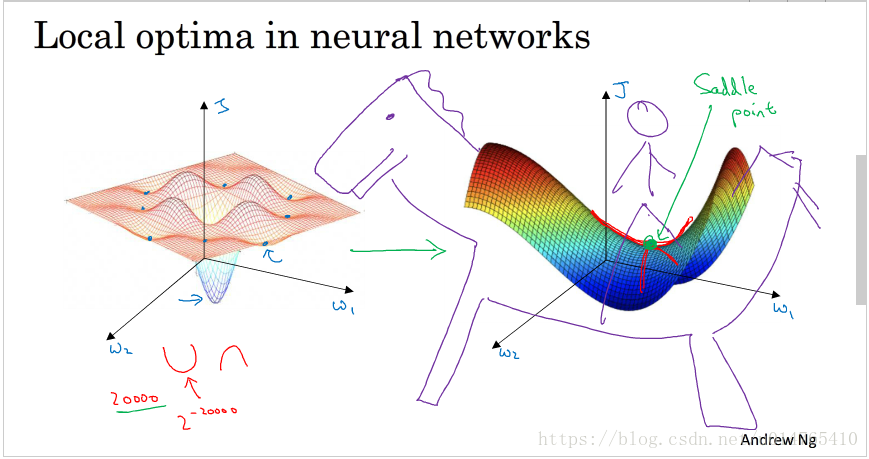
Note that：从上面的示例也可以看出，我们对于low dimension space的认识，并不能直接转嫁到high dimension space。

超参数调试

各个hyperparameter的重要程度，如下图所示：

notation interpretion：
alpha: learning rate
beta：指数加权平均的参数
beta1,beta2,ekson：Adam算法的hyperparameter
the importance of hyperparameter：红色方框内超参数第一重要；黄色方框内超参数第二重要；紫色方框内超参数第三重要；蓝色字体为一些超参数默认值；

如何选取超参数值

• 比起规则选取，随机选取，更有可能探究到best hyperparameter，如下图所示，如果采用规则选取，则hyperparameter1最多可选取5个点（左图），而如果采用随机选取，则hyperparameter1可以选取25个点（右图）。
  
  通过上述的随机选取，可以初步确定一个最优hyperparameter的范围，在该范围内，在密集布点，寻求最优的hyperparameter。
  
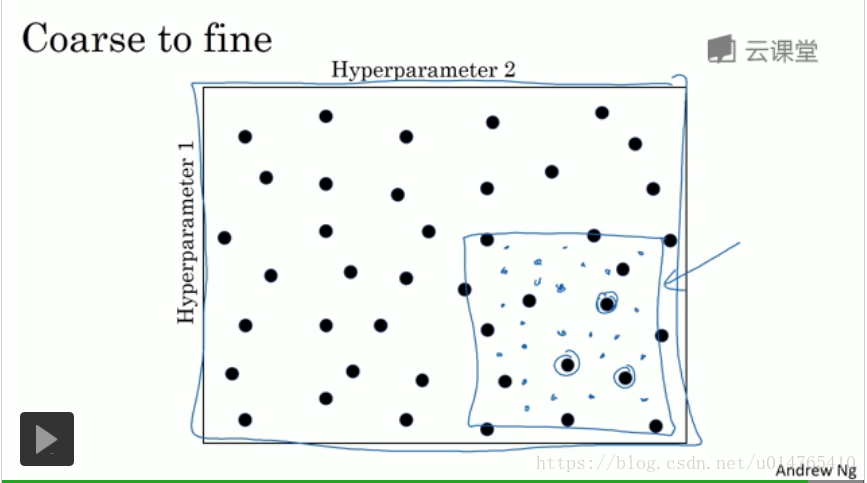
• 为hyperparameter选择合适的范围
  首先说明learning rate的选取：
  错误的做法是，直接让alpha = np.random(0.0001,1)，因为，这样做，alpha落在区间[0.1,1]的概率为90%，而只有10%的概率会落在[0.0001,0.1]，而我们希望的是，alpha可以均匀的落在区间：0.0001-0.001-0.01-0.1-1，可以采用的做法如下：
  r= -4 * np.random.rand()
  alpha=10^r
  或者是：
  令alpha belong to [10^a,10^b]
  r=np.random(a,b)
  alpha=10^r
  
  指数加权平均中的参数beta：
  如果想将beta的搜索范围限于[0.9,0.999]，错误的做法是直接使：beta=np.random(0.9,0.999)，这样无法到到均匀采样的效果，且beta在不同的区间内取值，对于指数加权平均会造成不同的影响，如：beta=0.9，or ,beta=0.9005，其加权平均基本都是取值last 10 samples，但是，如果beta=0.999，or，beta=0.99则其加权平均分别是在last 1000 ,last 100个samples上进行的，会影响最终的指数加权平均的走向。
  正确的做法是：限定1-beta的搜索范围为[0.1,0.001]，like alpha，令：
  r=np.random.(-3,-1)
  1-beta 为：10^r
  
  与learning rate和beta搜索范围定义不同，layer数目，以及hidden layer units数目的搜索范围可以直接采用np.random(a,b)的方式（a,b均为int）。
  在实际工作中，绘制不同hyperparameter下，cost function的走势，选择能够使cost function最小的hyperparameter。如果，服务器CPU足够的话，可以同时绘制不同hyperparameter下，cost function的走势，如果，服务器CPU不够的话，一次只绘制一个hyperparameter下，cost function的走势，隔几天后，改变hyperparameter的取值，查看cost function的走势，如果cost function升高的话，则说明该hyperparameter取值bad，舍掉。
  

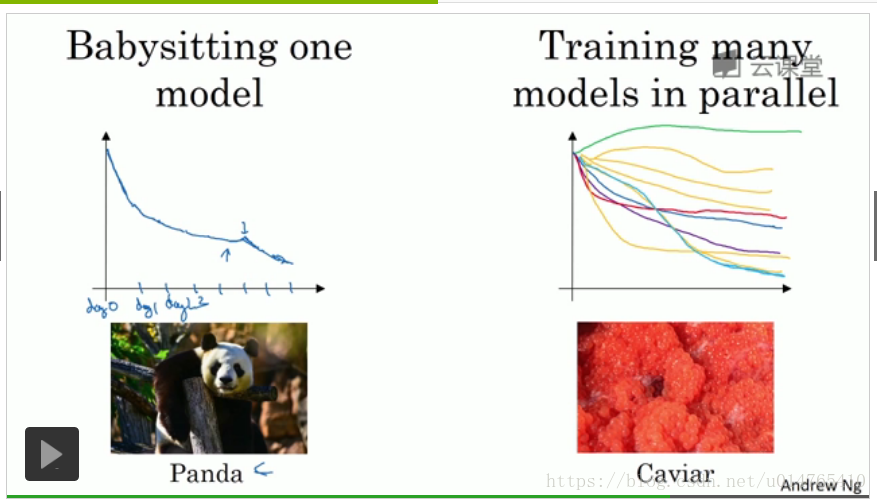
Batch 正则化

Batch正则化原理

Batch正则化，实施的是mini-batch gradient descent，其正则化的含义是针对各层hidden layer的z值展开的，具体过程如下：

在上述第3步求Znorm中，分母之所以要加入eclipson，是为了防止分母为0的情况发生。
在上述第4步中，引入gama和beta，是为了使Z拥有不同的mean和variance：如果不引入gama和beta，则Z的mean=0,variance=1，在activation function sigmoid中，Z值将集中在曲线中间部分，这会使得active function从sigmoid 转化为一个linear (如下图)，从而降低active function的power。

在logistic 中，我们将input 进行normalize(mean=0,variance=1)，能够加快学习的速度。在neural network中，我们可将batch norm应用于每一层hidden layer中，从而加快其学习速度，其实施过程如下：
step1：求hidden layer的z值；
step2：求z的batch norm，z_norm；
step3：将z_norm作为hidden layer中active function的输入；
step4：计算下一层hidden layer的z值，重复上述步骤1-3；
在batch norm中，gama和beta为parameter，同weight一样，可以通过gradient descent ，momentum，RMSprop，Adam获得更新方式（如：w := w - dw）。
具体步骤如下图所示：

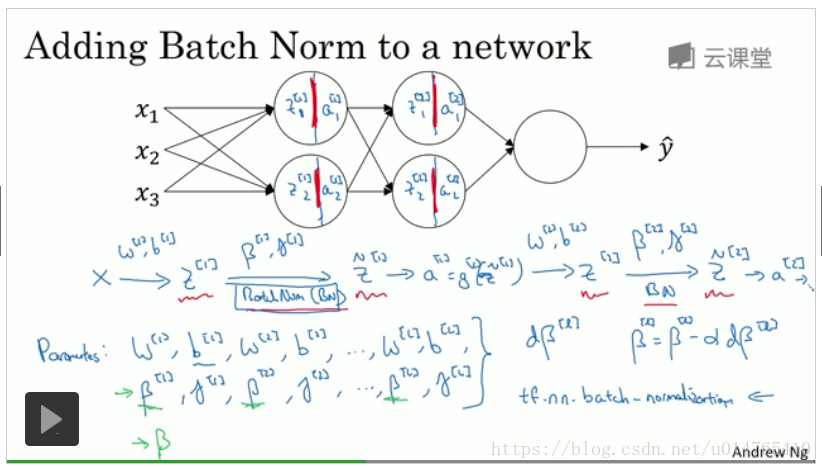
值得一提的是，如果neural network决定使用batch norm，则在计算z时，可以将b(截距)舍去，即：z=wx。这是因为，在计算z_norm时，将z去中心化时，同样会从z中去除b。

如何在预测test sample时使用batch norm

当用batch norm训练neural network时，在利用训练好的neural network进行test sample的预测时，首先要将test sample 进行 batch norm，具体操作如下：
way1：利用指数加权平均求test sample normalization中的mean和variance
step1：假设每一次iteration中得到的mean ,variance为m_i，v_i，i为iteration次数
step2：利用指数加权平均求最后一次iteration时的mean，variance:
将mean ,variance初始化为0
在每一次iteration i中执行下述步骤：
对于每一层的hidden layer：
mean := beta * mean + (1-beta) * m_i
variance := beta * variance + (1-beta) * v_i
最终得到的mean，variance即为test sample normalization的mean,variance。
way2：将所有的trainingdata一次性的投入训练好的neural network，利用batch norm的公式，求得每一层hidden layer的mean,variance。

batch norm的意义

• batch norm可以使得neural network对于input distribution的变化更加的robust：
  不管input的distribution为什么，至少可以保证每个hidden layer的z值mean和variance为定值，从而降低z distribution的变化程度，使得各个hidden layer的训练相对稳定，从而使neural network对于input 的变化具有更强的适应性。
• batch norm在一定程度上具有正则化的功能（但其主要用途并不是“正则化”）
  

softmax 回归

softmax是用来解决多分类问题的：在neural network的final layer使用softmax active fuction，输出的是各类的概率值，softmax function具体如下：
在求得 final layer z后：

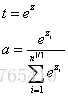
softmax-neural network的具体框架如下：

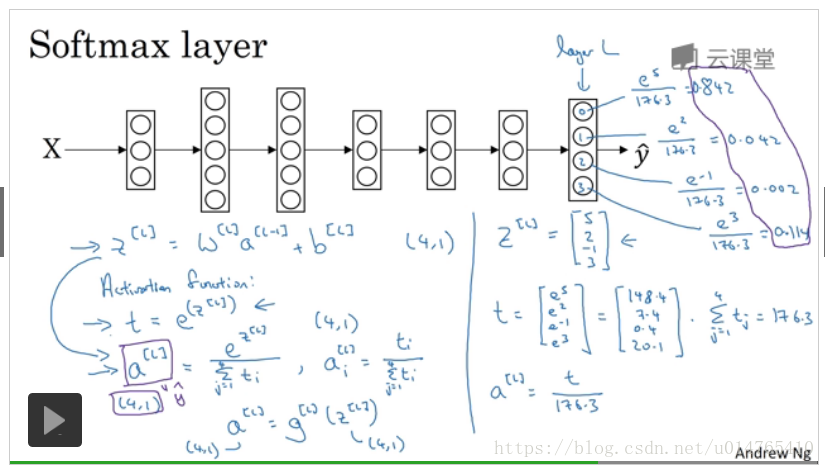
softmax的cost function是最大似然估计，如下PPT:

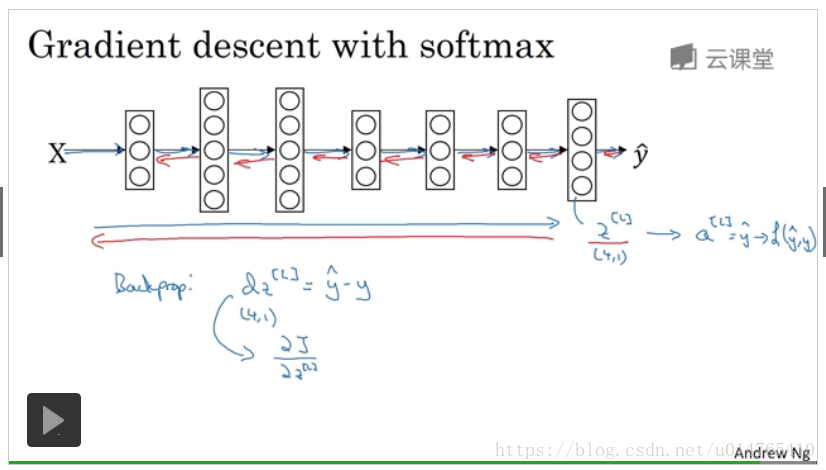
softmax的backward propagation中第一个;(similar to standard backward propagation in standard neural network）,如下PPT所示：

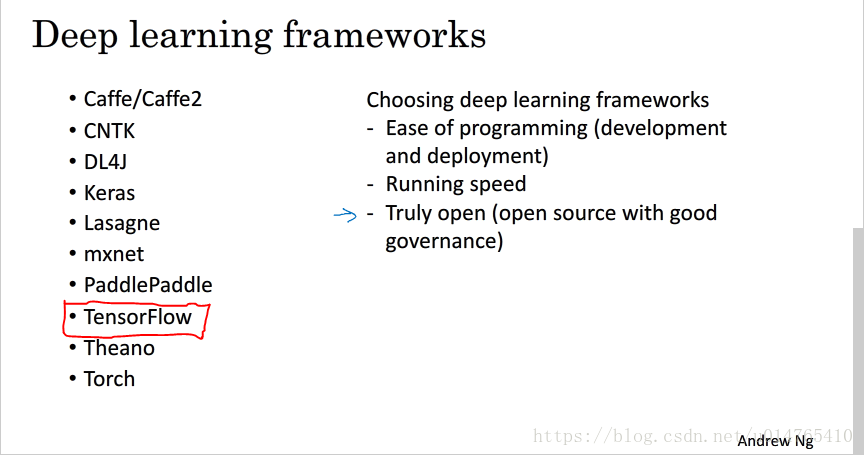
深度学习框架