磁悬浮轴承控制策略：电流环PID控制器设计及参数整定

磁悬浮轴承电流环被控制对象等效为RL串联电路模型，电路输入为电压，输出/控制目标为电流。电路拓扑如下：

图1 磁悬浮轴承电路等效模型​​

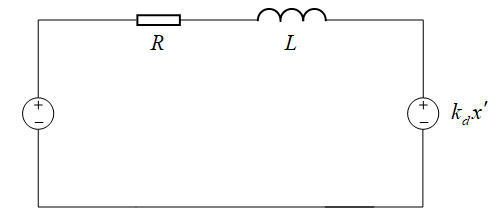
忽略反电势影响，电路微分方程及拉氏变换：

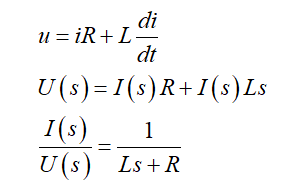
因此电路等效传递函数为：

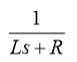
其中，L为标称电感，R为标称电阻。

考虑控制器采样时间T，同于PWM周期T，将系统延时等位为：

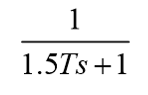
功率驱动增益为：Kpwm。

采用PI控制器，则系统框图为：

图2  磁悬电流环控制框图

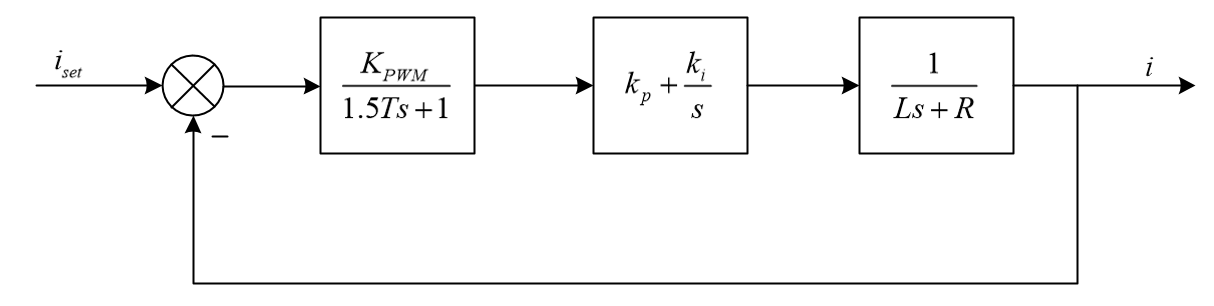
系统开环传递函数：

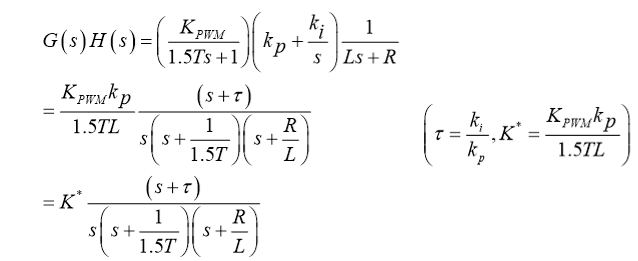
 通过零极点对消方法，得：

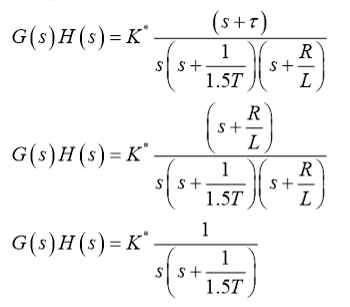
其中：

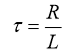
计算系统闭环传递函数，并按照典型II型系统最优阻尼比整定参数，得：

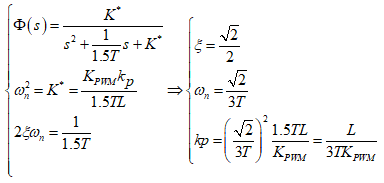
系统参数整定，计算kp、ki：

 将kp、ki带入系统闭环传递函数，并等效化简：

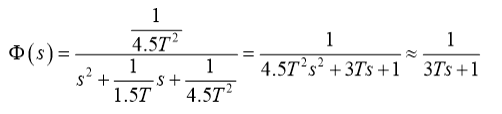
得电流环等效传递环数：

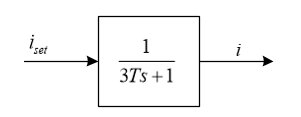
按如下设定系统参数，并计算控制参数：

单元	参数定义	参数	数值	单位
功率单元	电压	Udc	100	VDC
	开关频率	f	20000	Hz
	开关周期	T	0.00005	s
	桥臂增益	Kpwm	1	No
——	——	——	——	——
磁轴承参数	电感	L	5.36E-03	H
	电阻	R	0.15	Ω
——	——	——	——	——
电流环	根轨迹增益	K*	8.89E+07	No
	PID比例系数	Kp	3.57E+01	No
	PID积分系数	Ki	1000	No
	惯性时间常数	Ts	150	us
	响应时间95%	ts	450	us

在MATLAB/simulink搭建仿真模型：

图3 仿真模型

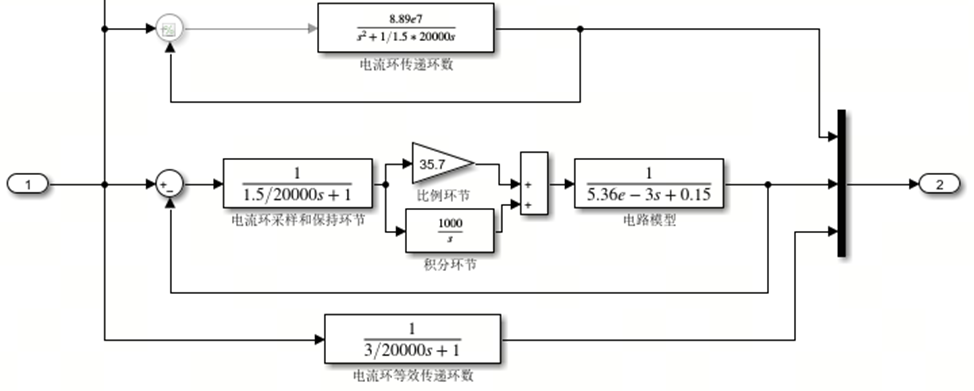
根据所搭建传递函数，分析系统响应时间如下：

图4 系统阶跃响应

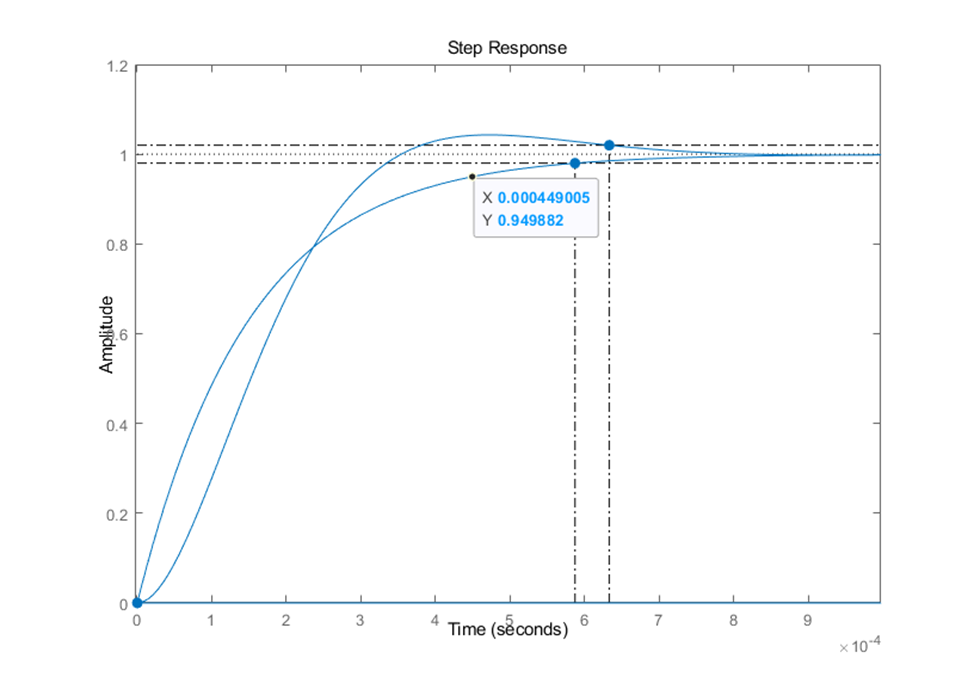
结果表明，阶跃响应时间仿真结果和计算结果基本一致 ，参数整定合理。