An Easy Problem?! - POJ 2826

最新推荐文章于 2020-12-13 20:49:05 发布

提比-我有特殊的AC技巧

最新推荐文章于 2020-12-13 20:49:05 发布

阅读量458

点赞数

CC 4.0 BY-SA版权

分类专栏： POJ 几何

本文链接：https://blog.youkuaiyun.com/u014733623/article/details/47778649

POJ 同时被 2 个专栏收录

206 篇文章

订阅专栏

几何

39 篇文章

订阅专栏

本文探讨了一个有趣的编程挑战：如何通过两块木板接取雨水的最大面积。文章详细介绍了输入格式、解题思路，包括如何判断木板是否平行、是否有交点、如何计算交点以及如何处理精度问题。提供了简洁的AC代码实现，帮助读者理解并解决类似问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

An Easy Problem?!

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 10792		Accepted: 1622

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.

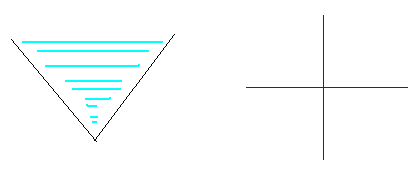
Your mission is to calculate how much rain these two boards can collect.

Input

The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one.

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.

Sample Input

Sample Output

1.00
0.00

题意：用木板去接雨水，问最多接多少面积的雨水。

思路：1、判断是否和y轴平行，是否有交点。不符合的直接输出0；

2、求出交点

3、得到两个木板到交点所在竖直直线的夹角，判断木板是否在同一边。如果在同一边，还要判断上面的木板是否覆盖下面的木板使得雨水无法进入。

4、处理精度。

我的代码比起网上其他人的代码还是比较简短的，可以借鉴下。

AC代码如下：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){}
};
double PI=acos(-1.0),eps=1e-8;
typedef Point Vector;
Vector operator + (Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator * (Vector A,double p){return Vector(A.x*p,A.y*p);}
Vector operator / (Vector A,double p){return Vector(A.x/p,A.y/p);}
int dcmp(double x){return (x>eps)-(x<-eps);}
double Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}
double Length(Vector A){return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}
bool SegmentIntersection(Point a1,Point a2,Point b1,Point b2)
{
    double c1=Cross(a2-a1,b1-a1);
    double c2=Cross(a2-a1,b2-a1);
    double c3=Cross(b2-b1,a1-b1);
    double c4=Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<=0 && dcmp(c3)*dcmp(c4)<=0
    &&dcmp(min(a1.x,a2.x)-max(b1.x,b2.x))<=0
    &&dcmp(min(a1.y,a2.y)-max(b1.y,b2.y))<=0
    &&dcmp(min(b1.x,b2.x)-max(a1.x,a2.x))<=0
    &&dcmp(min(b1.y,b2.y)-max(a1.y,a2.y))<=0;
}
bool jiaodian(Point a1,Point a2,Point b1,Point b2,Point &as)
{
    double s1=Cross(a1-b1,b2-b1);
    double s2=Cross(a2-b1,b2-b1);
    as=(a2*s1-a1*s2)/(s1-s2);
    return 1;
}
int T,t,n,m;
int main()
{
    int i,j,k;
    double c1,c2,h,ans;
    Point a,b,c,d,e,f;
    scanf("%d",&T);
    for(t=1;t<=T;t++)
    {
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y);
        if(a.y<b.y)
          swap(a,b);
        if(c.y<d.y)
          swap(c,d);
        if(dcmp(a.y-b.y)==0 || dcmp(c.y-d.y)==0 || SegmentIntersection(a,b,c,d)==0)
        {
            printf("0.00\n");
            continue;
        }
        jiaodian(a,b,c,d,e);
        f=Point(0,1);
        c1=fabs(Angle(a-e,f));
        c2=fabs(Angle(c-e,f));
        h=min(a.y,c.y)-e.y;
        if(c1>c2)
          swap(a,c);
        if(dcmp(a.x-e.x)*dcmp(c.x-e.x)<=0)
          ans=h*h*(tan(c1)+tan(c2))/2;
        else
        {
            ans=fabs(h*h*(tan(c1)-tan(c2))/2);
            if(dcmp(a.x-c.x)==0 || dcmp(a.x-e.x)==dcmp(a.x-c.x))
              ans=0;
        }
        if(dcmp(h)==0) //这里卡精度了
          ans=0;
        printf("%.2f\n",ans+eps);
    }
}