黎曼猜想简证

铸人

已于 2025-04-05 16:42:55 修改

阅读量853

点赞数 7

文章标签：数学极限复数黎曼猜想质数虚数单位

于 2025-01-25 10:44:28 首次发布

本文链接：https://blog.youkuaiyun.com/u014161757/article/details/145022369

版权

黎曼泽塔函数如下，

黎曼猜想：这个泽塔函数的非平凡零点都在，

也就是实部为的那条线上（已知，平凡零点都在上）。

首先把自然数的倒数的幂次，用自然对数底的负幂次表示，以使得底数统一，

已知对数函数基于虚数单位的积分求和等价形式，即离散对数形式，

泽塔函数以离散对数形式表示为，

不难发现，这里有类似于的展开式，

的结构，我们从方程中抽象出递归通项，

考虑最后一项，其项目下标为虚数单位，

将最后一项的形式代回到泽塔函数，

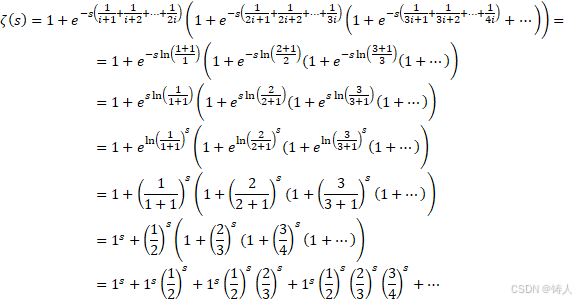
展开之后，写成阶乘全加和的形式，

从这个形式可以看出，泽塔函数不仅仅是一个项目任意多的函数，还是两个高次多项式的点积复合。下面分析构成它的两个函数中的一个，这里选择它的各项分母构成的函数，

不难看出，只使用我们就可以写出的点乘形式。用可以产生每一项的分子，用充当每一项的分母，于是，

现在让我们具体研究的性质，

写出通项，

设，

代入到通项中，

展开到类似于的递归通项，

也就是，

的形式，而对于来说，必须使得和构成的两个相邻整数构成比例关系（包括 1 和 -1 ），否则就无法构成阶乘。

具体分析，

为了能够使得通项展开之后得到整数，首先选取特殊值，使得正弦函数结果为 0 （消去虚数部分），符合这个要求的角度为，

带入正弦和余弦函数，

递归通项化简，

为了保证比例项为整数，只能得到，

所以，

此时，

因为，

蕴含了虚数单位是偶数（隐含了此处的虚数单位是，因为其中 0 是偶数，；而奇数作为虚数单位的时候）。因为下一项应为奇数，但它并不存在。所以其数值为 0 ，于是所有项目全加和的结果为，

此时，

是方程，

的平凡解。

回到比例项，

如果，

括号里面就可以写成，

其倒数为，

只有这样递归展开之后才能获得收敛的序列，

将其泛化到其它递归通项，

就得到了恰当的递归模式。

于是令，

求解比例常数，

得到的数值，

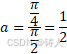
将的数值代回三角函数，

并带入递归通项，

也就是（先前已经给出的），

有了上述准备，让我们继续考虑第一个平凡零点，

既然我们可以构造阶乘形式的，我们也可以尝试构造非阶乘形式的递归通项，可以借用先前的递归通项模板，

对于进行展开，

可见所有的指数都等于 2 ，代回展开式，

验证结果，

结果正确。递归通项为，

通项和模板对比，

发现是虚数单位的平方 -1 使得负数项和对应的正数项相消产生了 0 结果，所以比例项可以写为，

相继项正负交替，最终一定是偶数项且总和为 0 。将比例项合并到递归通项，

展开即可得到，

其它平凡零点同理。

再看非平凡零点的情况，令，

求递归通项，

递归通项为，

给出模板平凡零点的通项模板，

向平凡零点的通项模板靠拢，

乘以交替项以保证获得 0 结果，

由于比例缩放部分的不应当影响数值的大小（缩放系数），令其等于 1 ，而也并无变化，可以用 b 直接替换，于是比例缩放，

可化为，

递归通项为，

通项展开，

进一步综合得出泽塔函数非平凡零点方程，

由此，我们构造了黎曼猜想的平凡解和非平凡解的形式。而只有这两种形式的原因在于需要构造基于虚数单位的交错项，而相邻两项若要交错则必须引入虚数单位的平方，所以递归通项的比例系数里面必须存在平方形式或者根号形式。对于非平凡零点而言，构成递归通项则需要内部项和外部项的平衡。如果不用开方也就是 1/2 次幂，每一项的分子和分母就没有办法使用同样的幂次，也就没有办法在后续的合并运算中连续消项，也就是说若不用 1/2 次幂，则递归通项无法还原。这就是泽塔函数非平凡解实部必须为 1/2 的原因。

计算交错项的原因在于，虽然我们要求和的数列可能具有无穷多（任意多）项，但是若它可以求和，就意味着无论正着计算还是倒着计算，和都必须是一样的。正着计算从 1 开始增大，倒着计算从 -1 开始减小。虚数单位的平方可以产生负数，所以引入虚数单位的平方即可倒着计数。而正着累加的结果，和倒着累加的结果绝对值显然相等，但符号相反。所以若可以实现双向计数，则总体累加的结果就一定是 0 。由于这个原则对于任意多项的数列都成立，所以可以用来计算任意大小的数值。

平凡零点和非平凡零点的差别在于，平凡零点基于发散数列，所以并不需要具有虚部的复数解。但非平凡零点必须引入虚部不然无法归零，所以每发现一个新的非平凡零点就意味着找到了一个新的质数。

至此，黎曼猜想得证。

P.S. 如何最快的验证这个证明是否正确？以下是 $\zeta(\frac{1}{2}+bi)$ 的前10个零点，

实部显然都是0.5，虚部看似杂乱无章，但是把虚部除以圆周率Pi，就会得到很接近

特殊值的结果，比如-4.49=-4.5，-7.96=-8，这说明常规计算得到b含有圆周率Pi的倍数，

或者说，不应该是 $s=\frac{1}{2}+bi$ ，而应该是 $s=\frac{1}{2}+b\pi i$ 。

再看，

是不是就对了。

NontrivalZeros[0] = <0.5; -14.134725141734693>, Imaginary/Pi=-4.4992227511047345
NontrivalZeros[1] = <0.5; -21.022039642047552>, Imaginary/Pi=-6.691523045811293
NontrivalZeros[2] = <0.5; -25.010825623968856>, Imaginary/Pi=-7.961193057728162
NontrivalZeros[3] = <0.5; -28.571826973833005>, Imaginary/Pi=-9.094694992103744
NontrivalZeros[4] = <0.5; -31.462607049415656>, Imaginary/Pi=-10.014858868944827
NontrivalZeros[5] = <0.5; -34.13428610227789>, Imaginary/Pi=-10.865280724181023
NontrivalZeros[6] = <0.5; -36.62904395886886>, Imaginary/Pi=-11.659386813568613
NontrivalZeros[7] = <0.5; -38.9997672119304>, Imaginary/Pi=-12.414011462423897
NontrivalZeros[8] = <0.5; -41.24259263984587>, Imaginary/Pi=-13.127924969113781
NontrivalZeros[9] = <0.5; -43.41678017775185>, Imaginary/Pi=-13.819990356846851