向量运算

零向量

任意一维都是0的向量，例如[0，0，0]，3D零向量。
零向量是唯一大小为零的向量，也是唯一一个没有方向的向量。但不是点，只是没有位移。

负向量

要得到任意向量的负向量，只需要简单的将向量的每个分量都变负。例如-[x,y,z]=[-x,-y,-z]。
向量变负，将得到一个和原向量大小相等，方向相反的向量。

注意，向量在图中的位置是无关紧要的，只有大小和方向才是最重要的

向量大小（长度或模）

推导：对2D中任意向量v，能构造一个以v为斜边的直角三角形，由勾股定理可知，对于任意直角三角形，斜边的长度的平方等于两直角边长度的平方和，则：

因此可以得到n维向量大小的计算公式：

标量和向量的乘法

运算方式：

1. 标量和向量不能相加，但是能相乘，得到的是一个与原向量平行，但长度不同或方向相反的新向量。
2. 向量乘以标量k的效果就是以因子|k|缩放向量的长度。
3. 向量也能除以非零标量，效果等同于乘以标量的倒数。
4. 计算方式，就是让n维向量的每一维都乘以标量k，例如：k [x,y,z] = [kx,ky,kz]

注意事项：

1. 标量与向量相乘时，不需要写乘号。将两个量挨着写即表示相乘（常将标量写在左边）
2. 标量和向量的乘法和除法优先级高于加法和减法。例如：3a+b = (3a)+b
3. 标量不能除以向量，并且向量不能除以另一个向量
4. 负向量能被认为是乘法的特殊情况，乘以标量-1

标准化向量

即单位向量（或法线）：方向与原向量方向相同，大小为1的向量。
计算公式：将向量除以向量的大小（模） v（norm） = v / ||v||
零向量不能被标准化，因为零向量没有方向。

向量的加减法

计算公式：两个向量的对应维度相加减，例如
[x,y,z] + [a,b,c] = [x+a,y+b,z+c]
[x,y,z] - [a,b,c] = [x-a,y-b,z-c]
[x,y,z] - [a,b,c] = [x,y,z] + (- [a,b,c])

点a到点b的向量，为b-a。

注意事项：

1. 向量不能和标量或维度不同的向量相加减。
2. 和标量加法一样，向量加法满足交换律，但向量减法不满足交换律。永远有 a+b=b+a，但是a-b=-(b-a)，仅当a = b时，a-b=b-a

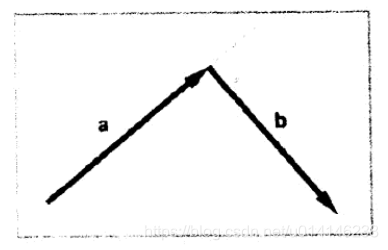
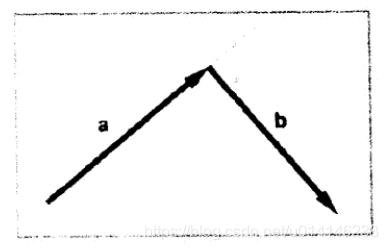
向量a和b相加的几何解释：平移向量，使向量a的头连接向量b的尾，接着从a的尾向b的头画一个向量。这就是向量加法的“三角形法则”。如图：

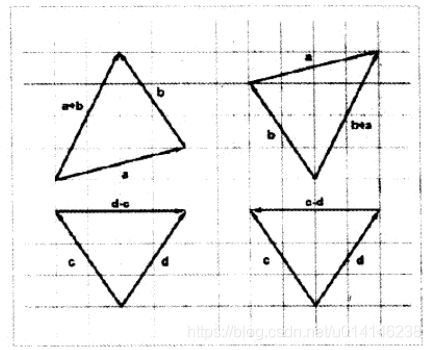
向量点乘（内积）

运算法则：
[a1,a2,a3…,an] 点乘 [b1,b2,b3…,bn] = a1b1+a2b2+a3b3…+anbn

几何解释：
点乘的结果描述了两个向量的相似程度，点乘结果越大，两向量越接近。

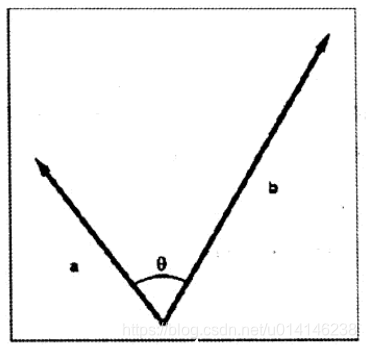
点乘等于向量大小与向量夹角的cos值的积：

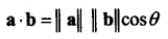
点乘结果判断角度范围：

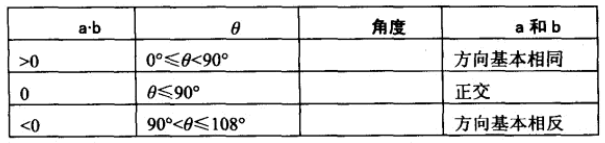
向量投影

示意图：

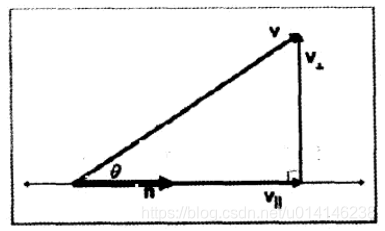
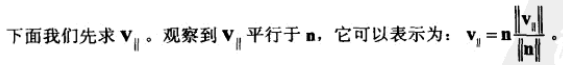
根据三角函数可得：

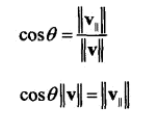
代入原公式得：

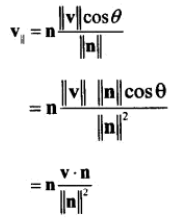
另一分量为：

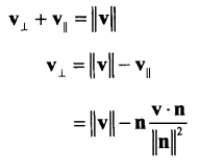
向量叉乘

仅可用于3D向量，和点乘不同，点乘得到一个标量并满足交换律，向量叉乘得到一个向量并且不满足交换律，但满足反交换律，即 a x b = -(b x a)。

运算法则：

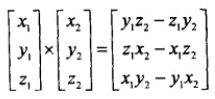
几何解释：
叉乘得到的向量垂直于原来的两个向量。


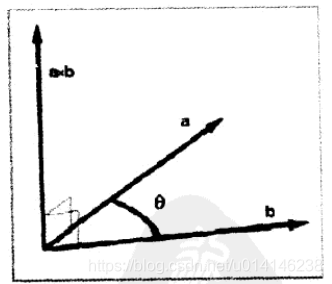
如果a，b平行或任意一个为0，则a x b = 0。叉乘对零向量的解释为：它平行于任意其它向量。注意这和点乘的解释不同，点乘的解释是和任意其它向量垂直。（当然，定义零向量平行或垂直于任意向量都是不对的，因为零向量没有方向。）

已经证明了a x b垂直于a、b。但是垂直于a、b有两个方向。a x b指向哪个方向呢？通过将a的头于b的尾相接，并检查从a到b是顺时针还是逆时针，能够确定a x b的方向。在左手坐标系中，如果a和b呈顺时针，那么a x b指向您。如果a x b呈逆时针，a x b远离您。在右手坐标系中，恰好相反。如果a和b呈顺时针，a x b远离您，如果a和b呈逆时针，a x b指向您。
顺时针图：

逆时针图：

注意：尾尾相连是用来求向量间的夹角，头尾相连决定顺时针还是逆时针方向。

线性代数公式