飞行控制 | 传感器原理、坐标转换、校准与数据融合

注：本文为 “飞行控制” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

基于四旋翼飞行器的陀螺仪、加速度计、磁力计传感器说明

williamgavin 原创于 2017-08-04 15:11:54 发布

本文详细介绍了陀螺仪、加速度计和磁力计的工作原理及其在飞行器中的应用，阐释了各传感器的特性，如陀螺仪测量旋转状态、加速度计检测受力情况、磁力计定位方位，并提供了传感器校准方法及飞行器 PID 调试步骤。

一、陀螺仪、加速度计和磁力计的定义及区别

1、陀螺仪、加速度计和磁力计的定义

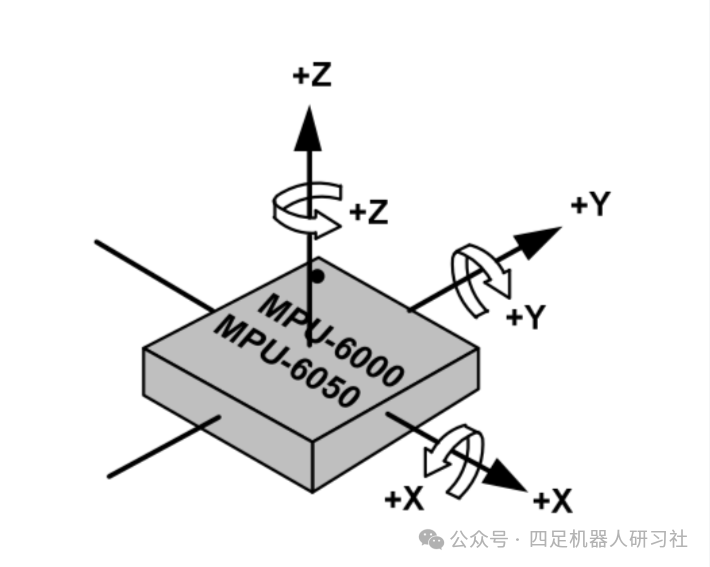
（1）陀螺仪（Gyroscope、GYRO-Sensor） 又称角速率传感器，三轴陀螺仪的工作原理是通过测量三维坐标系内陀螺转子的垂直轴与设备之间的夹角，计算角速度，进而判别物体在三维空间的运动状态。三轴陀螺仪可同时测定上、下、左、右、前、后等 6 个方向（合成方向可分解为三轴坐标），最终能够判断设备的移动轨迹和加速度。简言之，陀螺仪通过测量自身旋转状态确定设备当前运动状态，包括运动方向（向前、向后、向上、向下、向左、向右）及角速度变化（加速或减速），但无法实现设备方位（东、南、西、北）的判断。

（2）加速度计（Accelerometer、G-Sensor） 又称重力感应器，能够感知任意方向上的加速度（重力加速度仅为地表垂直方向的加速度）。加速度计通过测量组件在某一轴向的受力情况输出结果，表现形式为轴向的加速度大小和方向（$X$、$Y$、$Z$）。其与陀螺仪存在一定相似性，但陀螺仪更侧重测量设备自身的旋转情况（原位运动），而加速度计主要用于测量设备的受力情况，即三轴运动情况。尽管加速度计可能在小范围内换算出角速度，但受设计原理限制，更适用于空间运动判断。

（3）磁力计（Magnetic、M-Sensor） 又称地磁传感器，可用于检测磁场强度和方向，实现设备方位的定位。磁力计的工作原理与指南针类似，能够测量当前设备与东、南、西、北四个方向的夹角。

2、陀螺仪、加速度计和磁力计的功能优势

（1）陀螺仪：擅长测量设备的自身旋转运动。

（2）加速度计：擅长检测设备的受力情况。

（3）磁力计：擅长检测设备的方位。

3、具体应用场景

陀螺仪可感知“设备发生了旋转”，加速度计可感知“设备产生了直线位移（如向前移动若干距离）”，磁力计可感知“设备所处的方位（如朝向西方）”。

二、相关问答及技术说明

（1）飞行器传感器安装前校准的必要性

传感器的精度会随使用时间和温度变化而产生偏差，长期使用后会出现零点漂移现象，因此需要对传感器进行标定。传感器在使用过程中或存储后进行的性能复测称为校准，其本质与标定一致。若陀螺仪、加速度计和磁力计在安装前未进行校准，会直接影响飞行器的航向角（Yaw）、横滚角（Roll）和俯仰角（Pitch）的测量精度，进而影响飞行器的飞行稳定性和控制准确性。

（2）传感器校准的实现方法

• 磁力计校准：需将设备进行全方位 $720^{\circ }$ 旋转（整体旋转轨迹类似球体运动）。通过上位机记录磁力计的 $X$、$Y$、$Z$ 三轴原始数据，并将数据导入 Excel 表格进行处理。计算各轴数据的最大值与最小值的平均值，即 $\frac{\text{最大值}+\text{最小值}}{2}$，再将磁力计原始数据减去该平均值，即可大致消除零点漂移的影响。建议多次测量并计算，理想状态下多组测量结果的偏差应极小。经校准后，后续试验中通常无需再次对磁力计进行校准。

• 加速度计与陀螺仪校准：二者均有专用的校准语句，如下图所示：
  当上述语句赋值为 $1$ 时，表示启动校准；赋值为 $0$ 时，表示不进行校准。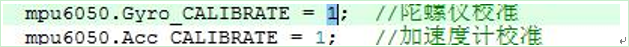

  

（3）飞行器 PID 调试方法及步骤

PID 调试的重点是明确调节目标，清晰分辨比例（P）、积分（I）、微分（D）参数取值过大或过小对系统的影响，且调试初期需确保四轴稳定时角速度为 $0$，若不为 $0$，需在原始数据中扣除偏差值。

• P 调节（比例调节）：只要被控对象存在误差，比例调节即会启动。参数取值过小会导致控制效果不佳；取值过大则会使系统不稳定，存在静差，施加外力后易出现震荡。实际调节中，应使系统处于“刚出现震荡但能最快稳定”的状态。（对应误差的当前状态）

• I 调节（积分调节）：只要被控对象存在静差，积分调节便会发挥作用，其主要功能是减小甚至消除静差。参数取值过小会导致系统不稳定；取值过大则会产生超调现象，引发震荡，同时会增加调节时间。实际调节中，建议先调节 P 参数、再调节 D 参数，最后调节 I 参数，前期通过 P、D 调节使系统效果达到较好水平，再通过 I 调节进一步提升系统稳定性。（对应误差的过去累积状态）

• D 调节（微分调节）：主要作用是加快调节响应速度，缩短调节时间，实现系统的快速响应。参数取值过小会导致调节时间过长，调节效果不佳；取值过大则会使系统不稳定，产生震荡。其本质是对未来误差的预测。（对应误差的未来变化趋势）

推荐调节思路：按 $P\to D\to I$ 的顺序调节，可使系统达到稳定状态。具体操作如下：先将 $D$、$I$ 参数置为 $0$，逐步增大 $P$ 参数，直至飞行器出现适当过冲并开始震荡；随后增加 $D$ 参数，削弱 $P$ 调节后期的作用，缓解过冲现象，直至无过冲；最后加入 $I$ 调节，优化系统稳定性。

第一步：调节内环 Pitch 通道

（1）将期望角度直接输入内环；
（2）修改输出参数，仅输出 $Pitch$ 相关值，即 KaTeX parse error: Expected 'EOF', got '_' at position 14: \text{posture_̲value}[0] = 0 -…，共输出 4 组数据；
（3）飞行器静止时，通过上位机观测角速度是否为 $0$，若不为 $0$，需在原始数据中扣除偏差值（理论上静止状态下角速度应为 $0$，实际存在偏差时需进行修正）；
（4）在匿名上位机中输入 PID 参数，反复调试直至角度稳定；
（5）将确定的 PID 参数写入程序文件（$parameter.c$）；
（6）下载程序至飞行器。

第二步：调节外环 Pitch 通道

（1）启用外环控制，将外环输出作为内环输入，同时将期望值输入外环；
（2）修改外环 PID 参数，直至施加外力后，飞行器能快速恢复至角度为 $0$ 的初始位置；
（3）将确认的 PID 参数写入程序文件；
（4）下载程序并进行验证。

第三步：调节 Roll 通道内环参数

调试方法与“调节内环 Pitch 通道”一致。

第四步：调节 Roll 通道外环参数

调试方法与“调节外环 Pitch 通道”一致。

第五步：系统微调

根据实际试飞情况，观察飞行姿态及误差，进行参数微调（若在调试架上已调试至最佳状态，实际飞行时通常不会出现明显问题）。

注意事项：当 Roll、Pitch 方向的 PID 参数调试完成后，需将 out_roll、out_pitch、out_yaw 三个参数赋值至 posture\_value}[] 数组中；若未完成该操作，飞行器飞行过程中易出现姿态失稳问题，进而引发翻机的安全风险。

三、参考资料

什么是陀螺仪、加速度计、磁力计

陀螺仪、加速度计、磁力仪等传感器汇总

---

无人机运动学控制中的坐标系及惯性坐标系与机体坐标系之间的矩阵转换、欧拉角

autotian 原创于 2019-10-24 17:33:23 发布

一、无人机控制中的坐标系

在无人机运动学研究中，涉及三种关键坐标系。

1.1 地球中心坐标系（ECEF）

地球中心坐标系的原点位于地心。X 轴通过格林尼治子午线与赤道的交点，正方向由原点指向该交点；Z 轴从原点指向北极；Y 轴与 X、Z 轴构成右手坐标系。

在该坐标系下，点的位置用 GPS 坐标表示时，对应 WGS-84 坐标系。WGS-84 坐标系中，X 轴指向 BIH（国际时间服务机构）1984.0 定义的零子午面（格林尼治子午线）与协议地球极（CTP）赤道的交点；Z 轴指向 CTP 方向；Y 轴与 X、Z 轴构成右手坐标系。

GPS 可获取 WGS-84 坐标系中的速度向量，为便于利用该速度向量进行无人机控制，需将其转换至无人机所在位置的“平面坐标系”。

1.2 NED 坐标系

由于地心坐标系下 GPS 信号的形式不便于直接应用于无人机控制，因此引入 NED 坐标系。NED 坐标系是导航计算中常用的坐标系，其三个坐标轴分别指向北、东、地，故又称北东地坐标系，三个方向保持固定。

当无人机搜星满足起飞条件后，该位置可确定为 NED 坐标系的原点。

1.3 机体坐标系

机体坐标系与飞行器固联，符合右手法则，原点位于飞行器重心处。X 轴指向飞行器机头前进方向，Y 轴由原点指向飞行器右侧，Z 轴方向通过 X、Y 轴按右手法则确定。机体坐标系是无人机惯性导航的基础坐标系，IMU（惯性测量单元）获取的加速度状态信息均为该坐标系下的数值。IMU 输出的 X 轴加速度信息，不能直接应用于 NED 坐标系。

无人机中的坐标转换，核心是 NED 坐标系（惯性系）与机体坐标系之间的转换。

二、无人机 IMU 单元

IMU 单元（惯性测量单元）是用于测量物体三轴姿态角（角速率）及加速度的装置。IMU 由陀螺仪和加速度计组成，具体功能如下：

• 陀螺仪：检测载体相对于导航坐标系的角速度信号；
• 加速度计：三个单轴加速度计分别检测物体在坐标系独立三轴的加速度信号。

IMU 的精度直接影响惯性系统的整体精度。

三、无人机中矩阵的确定与变换

3.1 无人机的姿态

空间中的无人机可通过其位置和方向进行完整描述。

设 $O-xyz$ 为标准正交坐标系，$\mathbf{x},\mathbf{y},\mathbf{z}$ 为其单位向量。图中无人机的参考点为 $O^{\prime }$，其在空间中的位置可表示为：

$${\mathbf{o}}^{\prime }=o_x^{\prime }\mathbf{x}+o_y^{\prime }\mathbf{y}+o_z^{\prime }\mathbf{z}$$

其中，$o_x^{\prime },o_y^{\prime },o_z^{\prime }$ 分别为无人机参考点 $O^{\prime }$ 在 $x,y,z$ 轴上的坐标分量。

$O^{\prime }$ 的坐标可简洁表示为列向量：

$${\mathbf{o}}^{\prime }=\left[\begin{array}{c}{o}_x^{\prime }\\ o_y^{\prime }\\ o_z^{\prime }\end{array}\right]$$

3.1.1 坐标系与无人机方向约束

通过坐标系 $O-xyz$ 可约束无人机位置，但无法约束其方向，后续将详细描述该坐标系的方向表征方法。

3.1.2 机身上坐标系的引入

为确定无人机方向，引入固连于无人机机身的坐标系 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$，$x^{\prime },y^{\prime },z^{\prime }$ 为该坐标系的单位向量，其与 $O-xyz$ 的转换关系为：

$$\{\begin{array}{l}{x}^{\prime }=x_x^{\prime }x+x_y^{\prime }y+x_z^{\prime }z\\ y^{\prime }=y_x^{\prime }x+y_y^{\prime }y+y_z^{\prime }z\\ z^{\prime }=z_x^{\prime }x+z_y^{\prime }y+z_z^{\prime }z\end{array}$$

3.2 旋转矩阵

（注：3.2 中旋转矩阵与 3.1 中式子各分量定义不一致，需结合式子定义理解）

描述无人机方向的 $x^{\prime },y^{\prime },z^{\prime }$ 可用矩阵表示为：

$$R=\left[\begin{array}{ccc}{x}^{\prime }& y^{\prime }& z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{x}_x^{\prime }& y_x^{\prime }& z_x^{\prime }\\ x_y^{\prime }& y_y^{\prime }& z_y^{\prime }\\ x_z^{\prime }& y_z^{\prime }& z_z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{x}^{\prime T}x& y^{\prime T}x& z^{\prime T}x\\ x^{\prime T}y& y^{\prime T}y& z^{\prime T}y\\ x^{\prime T}z& y^{\prime T}z& z^{\prime T}z\end{array}\right]$$

第三个矩阵中，因 $x$ 为单位向量 $(1,0,0)$，其与向量 $x^{\prime }$ 的点积结果即为 $x_x^{\prime }$ 的值。上述矩阵 $R$ 被称为旋转矩阵。

3.2.1 旋转矩阵的正交性

由于 $x^{\prime },y^{\prime },z^{\prime }$ 是正交坐标系下的单位向量，因此它们彼此正交且模长为 1，满足：

$$\{\begin{array}{l}{x}^{\prime T}{y}^{\prime }=0,y^{\prime T}{z}^{\prime }=0,z^{\prime T}{x}^{\prime }=0\\ x^{\prime T}{x}^{\prime }=1,y^{\prime T}{y}^{\prime }=1,z^{\prime T}{z}^{\prime }=1\end{array}$$

因此，$R$ 是正交矩阵，满足：

$$\begin{gathered} R^{T}R=I_3 \\ {R}^T=R^{-1} \end{gathered}$$

且有：

$$\det (R)=\pm 1$$

若坐标系遵循右手法则，则 $\det (R)=1$；若为左手法则，则 $\det (R)=-1$。

3.2.2 基本旋转

坐标系 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 可视为由坐标系 $O-xyz$ 通过基本旋转得到。旋转方向为逆时针时，旋转角度取值为正。

假定坐标系 $O-xyz$ 绕 $z$ 轴旋转角度 $\alpha$，其单位向量可表示为：

$$\begin{array}{rlrlrl}{\mathbf{x}}^{\prime }& =\left[\begin{array}{c}\cos \alpha \\ \sin \alpha \\ 0\end{array}\right]& {\mathbf{y}}^{\prime }& =\left[\begin{array}{c}-\sin \alpha \\ \cos \alpha \\ 0\end{array}\right]& {\mathbf{z}}^{\prime }& =\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\end{array}$$

因此，绕 $z$ 轴旋转的矩阵可表示为：

$$R_z(\alpha )=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]$$

同理，绕 $y$ 轴和绕 $x$ 轴旋转的旋转矩阵分别为：

$$R_y(\beta )=\left[\begin{array}{ccc}\cos \beta & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]$$

$$R_x(\gamma )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & -\sin \gamma \\ 0& \sin \gamma & \cos \gamma \end{array}\right]$$

这些矩阵可用于描述空间中的任意旋转。

通过上述矩阵可证明，旋转矩阵满足：

$$R_k(-\vartheta )=R_k^T(\vartheta )(k=x,y,z)$$

3.2.3 一个向量的旋转表述

为进一步理解旋转矩阵的几何意义，设两坐标系原点重合，即 $o^{\prime }=0$（$0$ 表示零向量）。

向量 $\mathbf{p}$ 可表示为：

$$\mathbf{p}=\left[\begin{array}{c}{p}_x\\ p_y\\ p_z\end{array}\right]$$

变换后的向量 ${\mathbf{p}}^{\prime }$ 可表示为：

$${\mathbf{p}}^{\prime }=\left[\begin{array}{c}{p}_x^{\prime }\\ p_y^{\prime }\\ p_z^{\prime }\end{array}\right]$$

3.2.3.1 坐标系间的点坐标变换

其中，$\mathbf{p}$ 和 ${\mathbf{p}}^{\prime }$ 分别对应同一空间点 $P$ 在坐标系 $O-xyz$ 和 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 中的坐标。

根据 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系到 $O-xyz$ 系的坐标转换关系，有：

$$\mathbf{p}=p_x^{\prime }{\mathbf{x}}^{\prime }+p_y^{\prime }{\mathbf{y}}^{\prime }+p_z^{\prime }{\mathbf{z}}^{\prime }=\left[\begin{array}{ccc}{\mathbf{x}}^{\prime }& {\mathbf{y}}^{\prime }& {\mathbf{z}}^{\prime }\end{array}\right]{\mathbf{p}}^{\prime }$$

令旋转矩阵 $\mathbf{R}=\left[\begin{array}{ccc}{\mathbf{x}}^{\prime }& {\mathbf{y}}^{\prime }& {\mathbf{z}}^{\prime }\end{array}\right]$，则坐标转换关系可表示为：

$$\mathbf{p}=\mathbf{R}{\mathbf{p}}^{\prime }$$

旋转矩阵 $\mathbf{R}$ 描述了向量从 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系到 $O-xyz$ 系的转换。由于旋转矩阵满足正交性 ${\mathbf{R}}^T\mathbf{R}=\mathbf{I}$（$\mathbf{I}$ 为单位矩阵），对上式两边左乘 ${\mathbf{R}}^T$，可得逆转换关系：

$${\mathbf{p}}^{\prime }={\mathbf{R}}^T\mathbf{p}$$

例 3.1：

设两坐标系原点重合，且 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系由 $O-xyz$ 系绕 $z$ 轴旋转 $\alpha$ 得到。由几何关系可得：

绕 $z$ 轴的坐标转换关系

点 $P$ 在 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系中的坐标为 ${\mathbf{p}}^{\prime }={\left[\begin{array}{ccc}{p}_x^{\prime }& p_y^{\prime }& p_z^{\prime }\end{array}\right]}^T$，绕 $z$ 轴旋转角度 $\alpha$ 后，在 $O-xyz$ 系中的坐标 $\mathbf{p}={\left[\begin{array}{ccc}{p}_x& p_y& p_z\end{array}\right]}^T$ 满足分量关系：

$$\{\begin{array}{l}{p}_x=p_x^{\prime }\cos \alpha -p_y^{\prime }\sin \alpha \\ p_y=p_x^{\prime }\sin \alpha +p_y^{\prime }\cos \alpha \\ p_z=p_z^{\prime }\end{array}$$

该转换关系可通过绕 $z$ 轴的旋转矩阵 ${\mathbf{R}}_z(\alpha )$ 表示为矩阵形式：

$${\mathbf{R}}_z(\alpha )=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]$$

即：

$$\mathbf{p}={\mathbf{R}}_z(\alpha ){\mathbf{p}}^{\prime }$$

旋转矩阵的几何意义

基于同一原点的两个坐标系间的坐标转换可通过旋转矩阵描述。旋转矩阵不仅定义了坐标系的方位关系，还刻画了向量在两个坐标系间的线性变换规则。

3.2.4 一个向量的旋转

3.2.3 节利用旋转矩阵实现了向量在不同坐标系间的转换，旋转矩阵还可表示同一坐标系下向量的旋转操作。

设 ${\mathbf{p}}^{\prime }$ 是 $O-xyz$ 系下的向量，$R\cdot {\mathbf{p}}^{\prime }$ 可生成一个与 ${\mathbf{p}}^{\prime }$ 模长相同的向量 $\mathbf{p}$。该性质可通过 $p^T\cdot p=p^{\prime T}\cdot R^T\cdot R\cdot p^{\prime }$ 及 $R^T\cdot R=I_3$ 证明。

例 3.2：

在 $O-xyz$ 系中，设位于 $xy$ 平面的向量 ${\mathbf{p}}^{\prime }$ 绕 $z$ 轴旋转 $\alpha$ 角。若 ${\mathbf{p}}^{\prime }$ 的坐标为 $p_x^{\prime },p_y^{\prime },p_z^{\prime }$，则旋转后的向量 $\mathbf{p}$ 可表示为：

$$\{\begin{array}{l}{p}_x=p_x^{\prime }\cos \alpha -p_y^{\prime }\sin \alpha \\ p_y=p_x^{\prime }\sin \alpha +p_y^{\prime }\cos \alpha \\ p_z=p_z^{\prime }\end{array}$$

该关系可用旋转矩阵简洁表示为：

$$\mathbf{p}=R_z(\alpha )\cdot {\mathbf{p}}^{\prime }$$

综上，旋转矩阵具有两项核心功能：一是描述两个坐标系之间的转换关系及向量在不同坐标系间的转换规则；二是实现同一坐标系下向量的旋转操作。

例 3.1 与例 3.2 的差异

两例分别对应旋转矩阵的两类应用场景。

	例 3.1（3.2.3 节）跨坐标系的向量转换	例 3.2（3.2.4 节）同坐标系的向量旋转
前提	含两个原点重合的坐标系（$O-xyz$ 与 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$），$O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系由 $O-xyz$ 系绕 $z$ 轴旋转 $\alpha$ 得到。	仅含一个坐标系（$O-xyz$），无额外坐标系。
描述对象	同一空间点 $P$ 在不同坐标系下的坐标转换（${\mathbf{p}}^{\prime }$ 为 $P$ 在 $O^{\prime }-x^{\prime }{y}^{\prime }{z}^{\prime }$ 系坐标，$\mathbf{p}$ 为 $P$ 在 $O-xyz$ 系坐标）。	同一坐标系下单个向量的旋转（${\mathbf{p}}^{\prime }$ 为旋转前向量，$\mathbf{p}$ 为旋转后向量，二者处于同一 $O-xyz$ 系）。
物理本质	坐标系方位变化导致点的坐标表示改变，点在空间中位置不变。	向量在空间中方向旋转，坐标变化源于自身方向改变，坐标系固定。
公式意义	体现不同坐标系间的向量转换规则，旋转矩阵 $R_z(\alpha )$ 作为坐标系间的转换桥梁。	体现同一坐标系下的向量旋转操作，旋转矩阵 $R_z(\alpha )$ 作为向量旋转的操作算子。

• 例 3.1 跨坐标系的坐标转换，不同坐标系下点坐标的换算；例 3.2 同坐标系的向量旋转，固定坐标系内向量的旋转实现；二者通过场景一致的数学形式，展现旋转矩阵的通用性。

• 旋转矩阵 $R_z(\alpha )$ 本质是线性变换算子，作用是对向量进行旋转式线性变换；

• 例 3.1 中，坐标系绕 $z$ 轴转 $\alpha$ 等价于向量绕 $z$ 轴转 $-\alpha$，因旋转矩阵正交性 $R_z(-\alpha )=R_z^T(\alpha )$，转换关系与向量直接旋转 $\alpha$ 形式一致；

• 例 3.2 中，直接对向量应用旋转算子 $R_z(\alpha )$，是线性变换的直接体现。

3.3 旋转矩阵的组合

为推导旋转矩阵的组合规则，考虑以共同原点 $O$ 为基础的三个坐标系 $O-x_0{y}_0{z}_0$、$O-x_1{y}_1{z}_1$ 和 $O-x_2{y}_2{z}_2$。向量 $\mathbf{p}$ 在这三个坐标系中的表示分别为 ${\mathbf{p}}^0$、${\mathbf{p}}^1$ 和 ${\mathbf{p}}^2$。

设 $R_i^j$ 表示坐标系 $i$ 转换至坐标系 $j$ 的旋转矩阵，则有：

1. ${\mathbf{p}}^1=R_0^1{\mathbf{p}}^0$（从 $O-x_0{y}_0{z}_0$ 系到 $O-x_1{y}_1{z}_1$ 系的转换）；
2. ${\mathbf{p}}^0=R_1^0{\mathbf{p}}^1$（从 $O-x_1{y}_1{z}_1$ 系到 $O-x_0{y}_0{z}_0$ 系的转换）；
3. ${\mathbf{p}}^0=R_2^0{\mathbf{p}}^2$（从 $O-x_2{y}_2{z}_2$ 系到 $O-x_0{y}_0{z}_0$ 系的转换）。

将第一式和第三式代入第二式，可得：

$$R_2^0=R_0^1{R}_2^1$$

该式描述了连续旋转的组合规则。初始坐标系 $O-x_0{y}_0{z}_0$ 通过 $R_2^0$ 旋转至 $O-x_2{y}_2{z}_2$ 系的过程可分解为两步：

1. 基于 $R_1^0$ 旋转，建立与 $O-x_1{y}_1{z}_1$ 系的联系；
2. 基于 $R_2^1$ 旋转，建立与 $O-x_2{y}_2{z}_2$ 系的联系。

所有旋转均可表示为一系列微小旋转的组合，每个旋转基于前一个坐标系进行，连续旋转的组合通过旋转矩阵的右乘实现。根据 $R_i^j$ 的性质 $R^T=R^{-1}$，可得：

$$R_i^j=(R_j^i{)}^{-1}=(R_j^i{)}^T$$

连续旋转也可基于固定坐标系描述，即所有旋转均参考初始坐标系 $O-x_0{y}_0{z}_0$ 进行。设 $R_1^0$ 为 $O-x_1{y}_1{z}_1$ 系基于 $O-x_0{y}_0{z}_0$ 系的旋转矩阵，$R_2^0$ 为 $O-x_2{y}_2{z}_2$ 系基于 $O-x_0{y}_0{z}_0$ 系的旋转矩阵（包含 $O-x_1{y}_1{z}_1$ 系基于 $R_2^1$ 的旋转），则有：

$$R_2^0=R_2^1{R}_1^0$$

其中，$R_2^0$ 为基于固定坐标系的连续旋转组合，通过单个旋转矩阵的左乘获得。

旋转组合的关键特性是矩阵乘法不满足交换律，因此两个旋转矩阵的组合结果依赖于单个旋转的执行顺序。

例 3.3：

下图展示了物体坐标系在不同旋转次序下的最终方向差异，直观体现了旋转顺序对结果的影响。

四、欧拉角

旋转矩阵包含九个元素，但由于正交矩阵的约束条件，这些元素并非完全独立（存在六个约束关系）。描述刚性物体的方向仅需三个独立参数，这种基于三个参数的方向描述称为最小表示。最小表示可通过角度集合 $\varphi =[\phi ,\upsilon ,\psi {]}^T$ 实现。

坐标系的基本旋转矩阵（3.2.2 节所述）是单个角度的函数，连续两次旋转的组合共有 27 种可能，其中 12 种符合物理意义（第一次旋转有 3 个轴可选，第二次旋转排除已选轴有 2 种选择，第三次旋转排除第二次所选轴有 2 种选择，总计 $3\times 2\times 2=12$ 种）。这 12 种组合均属于欧拉角的不同形式，本节重点介绍 ZYX（Roll-Pitch-Yaw）型欧拉角（滚转 - 俯仰 - 偏航）。

4.1 RPY 角

RPY 角起源于航海领域，属于 ZYX 型欧拉角，又称 Roll-Pitch-Yaw（滚转 - 俯仰 - 偏航），用于描述飞行器在空中的姿态变化。角度集合 $\varphi =[\phi ,\upsilon ,\psi {]}^T$ 可表示固定于飞行器质点的坐标系。

4.1.1 滚转 - 俯仰 - 偏航角的定义

滚转（Roll）、俯仰（Pitch）和偏航（Yaw）的定义与坐标系轴线设置相关，具体如下：绕 $x$ 轴的旋转为偏航角，绕 $y$ 轴的旋转为俯仰角，绕 $z$ 轴的旋转为滚转角。

对于飞机而言，机头方向指向 $z$ 轴正方向，$x$ 轴正方向定义为机身上方，坐标系设置如下图所示：

4.1.2 旋转矩阵与飞机坐标系

1. 绕 $z$ 轴旋转角度 $\psi$（偏航角），对应的旋转矩阵为 $R_z(\psi )$：

2. 绕 $y$ 轴旋转角度 $\theta$（俯仰角），对应的旋转矩阵为 $R_y(\theta )$：

3. 绕 $x$ 轴旋转角度 $\varphi$（滚转角），对应的旋转矩阵为 $R_x(\varphi )$：

坐标系旋转的组合结果可通过基于固定坐标系的基本旋转矩阵自左乘获得，即：

$$R(\varphi )=R_z(\phi )R_y(\psi )R_x(\theta )$$

展开后为：

$$\begin{array}{rl}R(\varphi )& =\left[\begin{array}{ccc}\cos \phi \cos \theta & -\sin \phi & \cos \phi \sin \theta \\ \sin \phi \cos \theta & \cos \phi & \sin \phi \sin \theta \\ -\sin \theta & 0& \cos \theta \end{array}\right]\left[\begin{array}{ccc}\cos \psi & 0& \sin \psi \\ 0& 1& 0\\ -\sin \psi & 0& \cos \psi \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]\\ & =\left[\begin{array}{ccc}{c}_{\phi }{c}_{\theta }& c_{\phi }{s}_{\theta }{s}_{\psi }-s_{\phi }{c}_{\psi }& c_{\phi }{s}_{\theta }{c}_{\psi }+s_{\phi }{s}_{\psi }\\ s_{\phi }{c}_{\theta }& s_{\phi }{s}_{\theta }{s}_{\psi }+c_{\phi }{c}_{\psi }& s_{\phi }{s}_{\theta }{c}_{\psi }-c_{\phi }{s}_{\psi }\\ -s_{\theta }& c_{\theta }{s}_{\psi }& c_{\theta }{c}_{\psi }\end{array}\right]\end{array}$$

其中，$c_{\cdot }=\cos (\cdot )$，$s_{\cdot }=\sin (\cdot )$。

设旋转矩阵 $R$ 为：

$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$

根据 ZYX 型欧拉角（滚转 $\varphi$、俯仰 $\theta$、偏航 $\psi$）与旋转矩阵的对应关系，可通过以下公式求解欧拉角：

• 当俯仰角 $\theta \in (-\pi /2,\pi /2)$（无人机常规姿态，无大角度翻转）时：
  $$\begin{array}{rl}\varphi & =\text{Atan2}(r_{21},r_{11})\\ \theta & =\text{Atan2}\left(-r_{31},\sqrt{r_{32}^2+r_{33}^2}\right)\\ \psi & =\text{Atan2}(r_{32},r_{33})\end{array}$$

• 当俯仰角 $\theta \in (\pi /2,3\pi /2)$（无人机大角度翻转，如倒飞、俯仰角超90°）时：
  $$\begin{array}{rl}\varphi & =\text{Atan2}(-r_{21},-r_{11})\\ \theta & =\text{Atan2}\left(-r_{31},-\sqrt{r_{32}^2+r_{33}^2}\right)\\ \psi & =\text{Atan2}(-r_{32},-r_{33})\end{array}$$

其中，$\text{Atan2}(y,x)$ 为双参数反正切函数，用于计算 $y/x$ 的反正切值（区别于单参数 $\arctan (y/x)$），可通过 $y$ 和 $x$ 的正负直接判断角度所在象限，从而确定 $[0,2\pi )$ 范围内的唯一角度值。

4.2 无人机中的欧拉角

结合前文旋转矩阵的相关知识，以下具体探讨其在无人机中的应用。

在无人机系统中，定义：

• 绕 $z$ 轴的旋转为偏航角（Yaw）；
• 绕 $y$ 轴的旋转为俯仰角（Pitch）；
• 绕 $x$ 轴的旋转为滚转角（Roll）。

如 3.2.2 节所述，基本旋转矩阵可用于将变换后的位移、速度、力转换为原坐标系下的对应物理量。若已知无人机相对于惯性系（NED 坐标系）的角度，即可确定其在惯性系下的运动状态。若以无人机机体坐标系为原始坐标系，需将机体坐标系下的变量转换至惯性系时，需乘以旋转矩阵的逆。由于旋转矩阵的逆等于其转置，转换矩阵表达式如下：

$$\begin{array}{rl}{R}_{b/m}& =R_{\varphi }{R}_{\theta }{R}_{\psi }\\ & =\left[\begin{array}{ccc}\cos \theta \cos \psi & \cos \theta \sin \psi & -\sin \theta \\ \sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi & \sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi & \sin \varphi \cos \theta \\ \cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi & \cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi & \cos \varphi \cos \theta \end{array}\right]\end{array}$$

其中，$R_{b/m}$ 表示以机体坐标系为原始坐标系，将机体坐标系下的变量转换至惯性系所需的旋转矩阵。

4.3 无人机中的万向锁

陀螺仪由一根穿过圆盘的轴线及高速旋转的圆盘（转子）组成。根据陀螺定轴性原理，陀螺的自转轴（竖直轴）在惯性空间内的方向保持不变。

---

无人机中的 IMU 单元（MEMS 三轴加速计、三轴陀螺仪、三轴磁力计）

autotian 原创于 2020-03-01 22:41:03 发布

1、三轴加速度计

（1）测量比力

三轴加速度计是一种惯性传感器，用于测量物体的比力。比力定义为去除重力后的整体加速度，或单位质量上所受的非引力作用力。当加速度计处于静止状态时，其可感知重力加速度，此时整体加速度为 $0$；当加速度计做自由落体运动时，整体加速度等于重力加速度，但传感器内部处于失重状态，此时三轴加速度计的输出为 $0$。

（2）测量角度

基于上述工作原理，三轴加速度计可用于测量角度。如图所示，加速度计内部弹簧的压缩量由传感器与地面的夹角决定，而比力可通过弹簧压缩长度间接测量。因此，在无外力作用的情况下，加速度计能够精确测量俯仰角和滚转角，且测量结果无累积误差。

MEMS 三轴加速度计的工作原理主要包括压阻式、压电式和电容式三种：

• 压阻式：比力（压力或位移）与传感器电阻变化成正比；
• 压电式：比力与传感器输出电压变化成正比；
• 电容式：比力与传感器电容变化成正比。

上述物理量的变化可通过对应的放大电路和滤波电路进行采集。该类传感器的显著缺点是受振动干扰影响较大。

受测量原理限制，三轴加速度计无法测量偏航角。

可测量俯仰角和横滚角：

2、三轴陀螺仪

功能

用于测量无人机的角速度，并通过对角速度积分计算得到角度信息。

工作原理

理解三轴陀螺仪的工作原理需以科里奥利力为基础。

科里奥利力定义

当质点相对惯性系做直线运动时，因自身惯性，其相对旋转体系的运动轨迹会呈现曲线形态。为描述该轨迹偏移现象，在旋转体系中引入虚拟力——科里奥利力，其矢量表达式为：
$${\vec{F}}_c=-2m\vec{\omega }\times \vec{v}$$
也可写为：${\mathbf{F}}_{\text{coriolis}}=-2m{}^b\omega \times v$

物理量及符号含义：

• $m$：质点质量
• $\vec{\omega }$（或${}^b\omega$）：旋转体系的角速度矢量；其中上标“$b$”是坐标系标识，代表物体固连坐标系（体坐标系），用于明确该矢量是在物体固连坐标系下描述的
• $\vec{v}$（或$v$）：质点相对惯性系的速度矢量
• “$\times$”：矢量叉乘运算

说明：
科里奥利力是虚拟力，并非真实作用力，仅用于在旋转参考系中描述“直线运动在旋转体系中呈现轨迹偏移”的现象。

陀螺仪结构与信号转换

陀螺仪内部设置两个运动状态的质量块，二者运动相位相差 $180^{\circ }$，即速度方向相反、大小相等。当陀螺仪发生旋转时，两个质量块会产生方向相反的科里奥利力，该力会压迫对应的电容极板产生位移，进而导致电容出现差分变化。电容变化量与旋转角速度成正比，通过检测电容变化即可间接获取旋转角度信息。

3、三轴磁力计

功能与原理

三轴磁力计可采集设备在 $X$、$Y$、$Z$ 三个轴向所受的磁场强度数据，该数据传入微控制器后，通过特定算法计算得到与磁北极相关的航向角，进而实现地理方位的检测。

磁力计通常由三个相互垂直的磁阻传感器组成，每个轴向的传感器负责检测该方向上的地磁场强度。

上图所示为采用晶体结构合金材料的磁阻传感器，其电阻值会随外界磁场强度的变化而改变，通过检测电阻变化可实现磁场强度的测量。

除磁阻式原理外，三轴磁力计还可基于洛伦兹力原理设计：电流在磁场中会受到洛伦兹力作用，该力驱动电容等元件产生物理变化，通过检测这种变化即可实现磁场强度与方向的测量。

---

IMU（陀螺仪、加速度计）& Magnetometer（磁力计）校准方法和流程

枯荣有常 原创于 2020-04-15 19:02:46 发布

本文详细介绍了惯性测量单元（IMU）与磁力计的校准原理及方法，探讨了地磁场特性及其在导航定位中的应用，通过十二位置标定法实现对加速度计、陀螺仪及磁力计的全面校准。

一、校准的定义与目的

1、校准目的

传感器在生产过程中，受工艺精度、技术水平等因素影响，存在固有缺陷，导致实际应用中测量数据存在误差。校准的关键是通过特定方法修正这些误差，提升测量精度。

2、出厂校准与用户校准

一般情况下，传感器厂商会在产品出厂前进行初步校准。以 Sensonor 公司的 Stim300 传感器为例：

用户采购 IMU 器件后，通常需进一步校准，校准参数主要包括零偏稳定性、比例因子（含温度特性）、非正交性等。批量应用与单个试验样机的校准方式及参数选择存在差异，下文重点阐述单个 IMU（含加速度计、陀螺仪）的校准方法。

3、坐标系定义与基础方程

（1）坐标系设定

• 导航坐标系：东-北-天（East-North-Up, ENU）；
• 载体坐标系：右-前-上（Right-Front-Up, RFU）。

（2）重力矢量与地球自转角速度

重力矢量和地球自转角速度在地理坐标系下的表达式如下：

（3）速度微分方程

速度微分方程为：

当传感器处于静止状态时，方程左侧速度微分为 $0$，右侧第二项（地球自转角速度相关项）可忽略，仅保留第一项（比力相关项）和第三项（重力相关项），此时需确保载体坐标系与导航坐标系的转换矩阵 $C_{nb}$ 为已知量。

4、校准条件

• 基础校准（零偏与比例因子）：传感器需保持静止且处于水平状态；

• 非正交性参数校准：需将载体坐标系的 $X$、$Y$、$Z$ 三轴分别与导航坐标系的对应轴平行，确保转换矩阵 $C_{nb}$ 为单位矩阵，此时比力满足 $f_b=f_n$（$f_b$ 为载体坐标系比力，$f_n$ 为导航坐标系比力）。

  

二、IMU 校准

1、加速度计校准

（1）校准方法：六位置校准法

该方法可校准 $X$、$Y$、$Z$ 三轴的零偏（Bias）和比例因子（Scale Factor Error），共 6 个参数。

（2）校准原理与公式

分别将加速度计的 $Z$、$X$、$Y$ 轴朝向重力方向与反重力方向，通过测量各位置的输出值，计算零偏和比例因子：

（3）注意事项

若载体坐标系定义为“前-右-上”（Front-Right-Up, FRU），则比例因子与重力加速度的乘积项 $(1+s)\cdot g$ 的符号需反向，具体如下：

2、陀螺仪校准

（原文未提供具体校准方法，此处保留原结构，待补充相关技术细节）

三、磁力计校准

1、地磁场特性

地球磁场的分布类似于条形磁体，磁场方向由磁南极指向磁北极：

• 磁极点处：磁场与当地水平面垂直；
• 赤道处：磁场与当地水平面平行；
• 北半球：磁场方向倾斜指向地面。

磁感应强度的单位为特斯拉（Tesla, T）或高斯（Gauss, G），二者换算关系为 $1\text{T}=10^4\text{G}$。地磁场强度随地理位置变化，通常范围为 $0.4\text{G}\sim 0.6\text{G}$。需注意，磁北极与地理北极并不重合，二者夹角约为 $11.5^{\circ }$。

2、地球磁场分布图

3、地磁要素

（1）坐标系与要素定义

以观测点 $O$ 为原点建立地理坐标系 $OXYZ$：$X$ 轴指向北，$Y$ 轴指向东，$Z$ 轴垂直指向地面。

地磁场强度矢量 $\vec{T}$ 的各分量定义如下：

• 北向分量 $B_n$：$\vec{T}$ 在 $X$ 轴的投影；
• 东向分量 $B_e$：$\vec{T}$ 在 $Y$ 轴的投影；
• 垂向分量 $B_z$：$\vec{T}$ 在 $Z$ 轴的投影；
• 水平分量 $B_h$：$\vec{T}$ 在水平面 $O-XY$ 的投影；
• 磁偏角 $D$：磁子午面（$B_h$ 与 $B_z$ 所在平面）与地理子午面（$O-XZ$ 平面）的夹角，东偏为正，西偏为负；
• 磁倾角 $I$：$\vec{T}$ 与水平面 $O-XY$ 的夹角。

上述 $T$、$B_h$、$B_n$、$B_e$、$B_z$、$D$、$I$ 统称为地磁场七要素，已知其中 3 个独立要素即可推导其余要素。

（2）要素间数学关系

$$\{\begin{array}{l}{B}_h=\sqrt{B_n^2+B_e^2}\\ T=\sqrt{B_h^2+B_z^2}=\sqrt{B_n^2+B_e^2+B_z^2}\\ \tan D=\frac{B_e}{B_n}\\ \sin I=\frac{B_z}{T}\\ \cos I=\frac{B_h}{T}\\ \tan I=\frac{B_z}{B_h}\end{array}$$

4、中国地磁要素分布

中国境内地磁场要素的大致分布情况如下：

• 总磁场强度 $T$：$0.41\text{G}\sim 0.60\text{G}$；
• 水平分量 $B_h$：由南至北从 $0.4\text{G}$ 降至 $0.21\text{G}$；
• 垂向分量 $B_z$：由南至北从 $-0.1\text{G}$ 增至 $0.56\text{G}$；
• 磁倾角 $I$：由南至北从 $-10^{\circ }$ 增至 $70^{\circ }$；
• 磁偏角 $D$：由东向西从 $-11^{\circ }$ 增至 $5^{\circ }$，零偏线由北向南经甘肃安西及西藏得宋地区。

5、地磁场的一级近似

不考虑地磁轴与地球自转轴的偏离问题，地磁强度分量可用以下解析式来描述：

实际运算中，需将磁力计在水平面 $X$、$Y$ 轴的测量值投影至北向，东向分量置零。

6、十二位置标定法

加速度计与磁力计的校准常采用十二位置标定法，该方法覆盖 36 个轴向。标定过程中，载体坐标系定义为“前-上-右”（Front-Up-Right, FUR），导航坐标系定义为“北-天-东”（North-Up-East, NUE），具体位置如下表所示：

十二位置标定法位置分布表

位置序号	1	2	3	4	5	6	7	8	9	10	11	12
第一轴（X 轴）	北	南	南	北	天	天	地	地	北	南	北	南
第二轴（Y 轴）	天	天	地	地	南	北	北	南	西	东	东	西
第三轴（Z 轴）	东	西	东	西	东	西	东	西	天	天	地	地

各方向轴向分布统计表

由上表可知，$X$、$Y$、$Z$ 三轴在每个方向（北、南、天、地、东、西）均出现 6 次，具体分布统计如下表：

方向	出现次数	方向	出现次数	方向	出现次数	方向	出现次数	方向	出现次数	方向	出现次数
北	6	南	6	地	6	天	6	西	6	东	6

通过在上述 12 个位置分别采集传感器输出数据，结合地磁场与重力场的已知特性，可建立校准模型，求解零偏、比例因子、非正交性等误差参数，实现加速度计与磁力计的全面校准。

参考资料

1. 《自主定位定向技术》
2. 《Applications of Magnetoresistive Sensors in Navigation Systems》
3. 《三轴磁阻式传感器标定方法研究》
4. 《一种十二位置不对北的磁罗盘标定方法》
5. 《基于 WMM 2005 的地磁计算》
6. ST 集成传感器方案实现电子罗盘功能
7. 地磁导航的应用风口来了？
8. 以 IndoorAtlas 为基础，百度地图将深度整合地磁定位技术
9. 高三物理复习微专题 1—《地磁场》
10. 椭球面

---

【传感器】IMU（加速度计 + 陀螺仪）PI 数据融合及解算四元数、求解欧拉角

-Y--Y-_ 原创于 2021-12-15 16:31:26 发布

本文从入门视角解析 IMU 数据，介绍加速度计与陀螺仪的作用、原始数据到有效姿态信息的转换逻辑，详细讲解姿态估计、四元数转换、欧拉角计算，以及加速度计（Accelerometer）与陀螺仪（Gyroscope）的数据融合过程，并结合实例代码展示基于 MPU9250 的姿态估计与滤波实现。

关键问题解析（入门视角）

1. IMU 输出数据及物理意义

以 BMI088 为例，其由加速度计和陀螺仪组成，输出数据的物理意义如下：

• 加速度计：单位为 mG（1 mG = 0.0098 m/s²），测量机体坐标系下三轴加速度。静止时仅受重力（1G = 1000 mG），满足 $\sqrt{a_x^2+a_y^2+a_z^2}\approx 1000\text{mG}$；
• 陀螺仪：单位为 °/s，测量绕机体坐标系 X、Y、Z 轴的旋转角速度。

（注：测量范围、精度等参数暂不展开。）

2. 目标数据与坐标转换逻辑

以云台应用为例，需获取世界坐标系（n 系） 下的偏航角（yaw，绕 Z 轴）和俯仰角（pitch，绕 X 轴），坐标系定义如下：

• 世界坐标系（n 系）：X 轴向东，Y 轴向北，Z 轴向天；
• 机体坐标系（b 系）：X 轴指向云台正前，Y 轴指向云台正左，Z 轴向天。

基础原理

重力向量在 n 系中固定为 $[0,0,-g]$，加速度计可测得该向量在 b 系中的表示 $[a_x,a_y,a_z]$。通过两个坐标系对同一向量的不同描述，可求解坐标系变换关系，进而得到姿态角（pitch/roll），但无法直接推导 yaw（仅依赖重力无法感知绕 Z 轴旋转）。

四元数引入原因

直接对坐标变换矩阵（T 矩阵）微分求解姿态变化复杂度高，引入四元数可简化旋转微分计算，主要转换关系如下：

1. 四元数 $Q$ 转姿态矩阵 $T$：
   

2. 四元数与欧拉角转换：g角
   $$\left[\begin{array}{c}\phi \\ \theta \\ \psi \end{array}\right]=\left[\begin{array}{c}\text{atan2}(2(wx+yz),1-2(x^2+y^2))\\ \text{arcsin}(2(wy-zx))\\ \text{atan2}(2(wz+xy),1-2(y^2+z^2))\end{array}\right]$$

3. 一阶龙格库塔法推导四元数微分迭代形式：
   

4. 加速度计与陀螺仪融合（消除积分误差）：
   

3. 数据融合主要流程

1. 初始化：初始角度 $[0,0,0]$，对应四元数 $[1,0,0,0]$；
2. 估算重力向量：通过当前四元数将 n 系重力向量 $[0,0,G]$ 转换为 b 系估算值 $V$：
   
3. 计算误差：测量重力向量与估算值的叉积误差；
4. 误差补偿：将误差经 PI 调节后补偿到陀螺仪数据；
5. 迭代更新：求解新的四元数并单位化；
6. 转换输出：将四元数转为欧拉角（pitch/roll/yaw）。

实例代码实现

/***************************************************************************************
                                      声 明
    本项目代码仅供个人学习使用，可以自由移植修改，但必须保留此声明信息。移植过程中出现
其他不可估量的 BUG，天际智联不负任何责任。请勿商用！

程序版本：V1.01
程序日期：2018-1-26
程序作者：愤怒的小孩 E-mail：1138550496@qq.com
版权所有：西安天际智联信息技术有限公司
****************************************************************************************/
#include "imu.h"
#include "math.h"
#include "filter.h"
#include "mpu9250.h"
#include "control.h"
#include "ICM20948.h"

// 互补滤波权重
#define Kp_New      0.9f              
#define Kp_Old      0.1f              
// 物理量转换系数
#define Acc_Gain    0.0001220f        // 加速度AD值转G（满量程±4g，LSBa=2*4/65535.0）
#define Gyro_Gain   0.0609756f        // 陀螺仪AD值转°/s（满量程±2000°/s，LSBg=2*2000/65535.0）
#define Gyro_Gr     0.0010641f        // 陀螺仪AD值转rad/s（π/180 * LSBg）
// 姿态解算参数
#define Kp          1.50f             // 比例增益（加速度计/磁力计收敛速率）
#define Ki          0.005f            // 积分增益（陀螺仪零偏收敛速率）
#define halfT       0.005f            // 采样周期的一半（单位：s）

// 全局变量定义
FLOAT_ANGLE Att_Angle;                // 姿态解算后的欧拉角（yaw/pitch/roll）
FLOAT_XYZ   Gyr_rad, Gyr_radold;      // 陀螺仪数据（弧度制）
FLOAT_XYZ   Acc_filt, Gry_filt, Acc_filtold; // 滤波后加速度/陀螺仪数据
float       accb[3], DCMgb[3][3];     // 机体坐标系加速度、方向余弦阵（n→b）
uint8_t     AccbUpdate = 0;           // 加速度数据更新标志
float       q0 = 1, q1 = 0, q2 = 0, q3 = 0; // 四元数初始值
float       exInt = 0, eyInt = 0, ezInt = 0; // 积分误差

/************************** 快速计算 1/Sqrt(x) **************************/
static float invSqrt(float x)
{
    float halfx = 0.5f * x;
    float y = x;
    long i = *(long*)&y;
    i = 0x5f3759df - (i>>1);
    y = *(float*)&i;
    y = y * (1.5f - (halfx * y * y));
    return y;
}

/************************** 原始数据预处理 **************************/
void Prepare_Data(void)
{
    static uint8_t IIR_mode = 1;

    // 读取IMU原始数据并去零偏
    MPU9250_Read();    
    MPU9250_Offset();  

    // 加速度数据滤波（去极值滑动窗口滤波）
    SortAver_FilterXYZ(&MPU9250_ACC_RAW, &Acc_filt, 12);

    // 加速度AD值转物理量（m/s²）
    Acc_filt.X = (float)Acc_filt.X * Acc_Gain * G;
    Acc_filt.Y = (float)Acc_filt.Y * Acc_Gain * G;
    Acc_filt.Z = (float)Acc_filt.Z * Acc_Gain * G;

    // 陀螺仪AD值转物理量（rad/s）
    Gyr_rad.X = (float) MPU9250_GYRO_RAW.X * Gyro_Gr;
    Gyr_rad.Y = (float) MPU9250_GYRO_RAW.Y * Gyro_Gr;
    Gyr_rad.Z = (float) MPU9250_GYRO_RAW.Z * Gyro_Gr;

    // IIR低通滤波（加速度）
    if(IIR_mode)
    {
        Acc_filt.X = Acc_filt.X * Kp_New + Acc_filtold.X * Kp_Old;
        Acc_filt.Y = Acc_filt.Y * Kp_New + Acc_filtold.Y * Kp_Old;
        Acc_filt.Z = Acc_filt.Z * Kp_New + Acc_filtold.Z * Kp_Old;

        Acc_filtold.X = Acc_filt.X;
        Acc_filtold.Y = Acc_filt.Y;
        Acc_filtold.Z = Acc_filt.Z;
    }

    // 赋值加速度数组并标记更新
    accb[0] = Acc_filt.X;
    accb[1] = Acc_filt.Y;
    accb[2] = Acc_filt.Z;
    if(accb[0] && accb[1] && accb[2])
    {
        AccbUpdate = 1;
    }
}

/************************** IMU姿态解算（四元数+PI融合） **************************/
void IMUupdate(FLOAT_XYZ *Gyr_rad, FLOAT_XYZ *Acc_filt, FLOAT_ANGLE *Att_Angle)
{
    uint8_t i;
    float matrix[9] = {1.f, 0.0f, 0.0f, 0.0f, 1.f, 0.0f, 0.0f, 0.0f, 1.f};
    float ax = Acc_filt->X, ay = Acc_filt->Y, az = Acc_filt->Z;
    float gx = Gyr_rad->X, gy = Gyr_rad->Y, gz = Gyr_rad->Z;
    float vx, vy, vz;  // 估算重力向量（机体坐标系）
    float ex, ey, ez;  // 重力向量误差
    float norm;        // 归一化系数

    // 四元数平方项（减少重复计算）
    float q0q0 = q0*q0, q0q1 = q0*q1, q0q2 = q0*q2, q0q3 = q0*q3;
    float q1q1 = q1*q1, q1q2 = q1*q2, q1q3 = q1*q3;
    float q2q2 = q2*q2, q2q3 = q2*q3, q3q3 = q3*q3;

    // 加速度数据有效性判断
    if(ax*ay*az == 0) return;

    // 加速度计数据归一化（单位化重力向量）
    norm = invSqrt(ax*ax + ay*ay + az*az);
    ax *= norm;
    ay *= norm;
    az *= norm;

    // 四元数估算重力向量（机体坐标系）
    vx = 2*(q1q3 - q0q2);
    vy = 2*(q0q1 + q2q3);
    vz = q0q0 - q1q1 - q2q2 + q3q3;

    // 计算重力向量误差（叉积）
    ex = ay*vz - az*vy;
    ey = az*vx - ax*vz;
    ez = ax*vy - ay*vx;

    // 误差积分
    exInt += ex * Ki;
    eyInt += ey * Ki;
    ezInt += ez * Ki;

    // 陀螺仪数据补偿（PI调节）
    gx += Kp*ex + exInt;
    gy += Kp*ey + eyInt;
    gz += Kp*ez + ezInt;

    // 四元数微分更新（一阶龙格库塔）
    q0 += (-q1*gx - q2*gy - q3*gz) * halfT;
    q1 += (q0*gx + q2*gz - q3*gy) * halfT;
    q2 += (q0*gy - q1*gz + q3*gx) * halfT;
    q3 += (q0*gz + q1*gy - q2*gx) * halfT;

    // 四元数单位化
    norm = invSqrt(q0q0 + q1q1 + q2q2 + q3q3);
    q0 *= norm;
    q1 *= norm;
    q2 *= norm;
    q3 *= norm;

    // 构建方向余弦阵（n→b）
    matrix[0] = q0q0 + q1q1 - q2q2 - q3q3;
    matrix[1] = 2.f * (q1q2 + q0q3);
    matrix[2] = 2.f * (q1q3 - q0q2);
    matrix[3] = 2.f * (q1q2 - q0q3);
    matrix[4] = q0q0 - q1q1 + q2q2 - q3q3;
    matrix[5] = 2.f * (q2q3 + q0q1);
    matrix[6] = 2.f * (q1q3 + q0q2);
    matrix[7] = 2.f * (q2q3 - q0q1);
    matrix[8] = q0q0 - q1q1 - q2q2 + q3q3;

    // 四元数转欧拉角（Z→Y→X，单位：°）
    Att_Angle->yaw += Gyr_rad->Z * RadtoDeg * 0.01f;  // yaw（陀螺仪积分）
    Att_Angle->pit = -asin(2.f * (q1q3 - q0q2)) * 57.3f;  // pitch
    Att_Angle->rol = atan2(2.f * q2q3 + 2.f * q0q1, q0q0 - q1q1 - q2q2 + q3q3) * 57.3f;  // roll

    // 方向余弦阵赋值
    for(i = 0; i < 9; i++)
    {
        *(&(DCMgb[0][0]) + i) = matrix[i];
    }

    // 失控保护（调试时可注释）
    // Safety_Check();
}

参考资料

1. 四元数完全解析及资料汇总

2. mpu6050 姿态解算与卡尔曼滤波（1）数学

---

感知定位篇之 IMU：陀螺仪和加速度计及互补滤波

子墨_bupt 原创于 2024-04-17 09:00:00 发布

1. IMU 介绍

IMU（Inertial Measurement Unit，惯性测量单元）是检测/测量加速度与旋转运动的传感器，基于惯性定律实现，涵盖从毫米级 MEMS 器件到高精度激光陀螺/光纤陀螺等类型。

组成部分

基础 6 轴 IMU 包含：

• 3 轴陀螺仪：测量绕 X/Y/Z 轴的旋转角速度（单位：°/s）；
• 3 轴加速度计：测量 X/Y/Z 轴的线加速度（单位：m/s²），静止时可感知重力加速度（9.8 m/s²）。

应用意义

陀螺仪的漂移误差对惯导系统位置误差的影响为时间三次方函数，高精度陀螺仪制造难度大、成本高，是影响惯性系统性能的重要因素。

2. 陀螺仪

2.1 陀螺仪测量原理

陀螺仪仅测量瞬时角速度（不直接输出姿态），姿态角需通过角速度积分得到：
$${\theta }_t={\theta }_{t-1}+\omega \cdot \Delta t$$
其中：

• ${\theta }_t$：当前角度；
• ${\theta }_{t-1}$：上一时刻角度；
• $\omega$：采样时刻角速度；
• $\Delta t$：采样时间间隔。

实际应用中仅能获取离散采样信号，假设 $\Delta t$ 内角速度恒定，通过累加实现积分。

2.2 陀螺仪零飘

误差来源

零飘（零偏）：静止时陀螺仪输出角速度非 0，而是在某一值附近波动；温漂：零偏随温度变化。二者会导致积分误差随时间累积，最终姿态失效。

校准方法

上电后采集 1000 帧静止状态下的陀螺仪原始数据，计算方差（判断是否静止，方差 < 阈值则有效），以标准差作为零偏值；积分前将原始数据减去零偏，可显著降低漂移。

3. 加速度计

测量特性

加速度计测量三轴线加速度，消费级器件高频噪声大，单独使用效果差，主要误差来源：

• 轴间误差：三轴实际安装角度偏离 90°（如 88°），非严格正交；
• 尺度误差：测量值与真实加速度比例偏移（如 1 m/s² 实际测为 0.8 m/s²）。

校准方式

可通过椭球拟合、6 面法标定补偿上述误差（部分场景如扫地机可省略）。

姿态解算价值

静止/匀速运动时，重力加速度方向固定（竖直向下），通过其在三轴的投影可推导俯仰角、滚转角，但无法感知偏航角（绕竖直轴旋转不改变重力投影）。

4. 滤波融合

传感器特性对比

传感器	短期特性	长期特性	主要误差
陀螺仪	精度高、响应快	积分漂移严重	零飘、温漂
加速度计	噪声大、响应慢	重力方向稳定	高频噪声、轴间/尺度误差

4.1 互补滤波

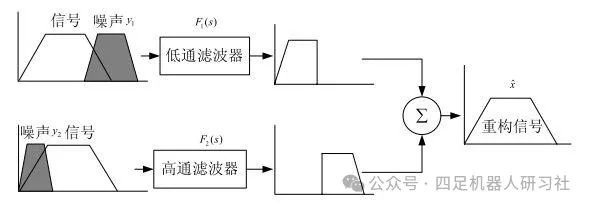
设计思路

通过高通滤波器保留陀螺仪高频有效信号（滤除低频漂移），低通滤波器保留加速度计低频有效信号（滤除高频噪声），融合后获得全频段稳定的姿态角。

简化版互补滤波

$$\theta =k\cdot {\theta }_{\text{gyro}}+(1-k)\cdot {\theta }_{\text{acc}}$$
其中：

• $0<k<1$：权重系数（k 越大越信任陀螺仪，反之信任加速度计）；
• ${\theta }_{\text{gyro}}$：陀螺仪积分角度；
• ${\theta }_{\text{acc}}$：加速度计解算角度。

进阶版互补滤波

低通滤波器 $LPF=\frac{C}{C+s}$，高通滤波器 $HPF=\frac{s}{C+s}$，其中 $C$ 为滤波系数（常数），$s$ 为微分算子（Laplace变换中的 $s$）。

融合公式：
$$\theta =\frac{s}{C+s}{\theta }_{\text{gyro}}+\frac{C}{C+s}{\theta }_{\text{acc}}$$

化简后的微分方程：
$$\dot{\theta }={\omega }_{\text{gyro}}-C(\theta -{\theta }_{\text{acc}})$$

其中：

• $\theta$：融合后的角度估计值。
• ${\theta }_{\text{gyro}}$：陀螺仪测量的角度（通过积分角速度得到）。
• ${\theta }_{\text{acc}}$：加速度计测量的角度（通过重力向量计算）。
• ${\omega }_{\text{gyro}}$：陀螺仪测量的角速度。
• $C$：滤波系数，可根据场景调整（如 $C=\tau$，其中 $\tau$ 为时间常数）。

其他融合方法

除互补滤波外，卡尔曼滤波是常用选择：基于状态估计模型，结合传感器噪声特性自适应调整权重，姿态估计精度更高。

参考资料

1. [什么是 IMU？-优快云 博客]
2. 说透互补滤波 (1) - 线性互补滤波器从原理到实现 - 知乎 (zhihu.com)

---

via:

• 基于四旋翼飞行器的陀螺仪、加速度计、磁力计传感器说明_加速度计 陀螺仪 区别-优快云 博客
  https://blog.youkuaiyun.com/williamgavin/article/details/76685789
• 无人机运动学控制中的坐标系，及惯性坐标系与机体坐标系之间的矩阵转换 欧拉角_无人机 坐标系转换-优快云 博客
  https://blog.youkuaiyun.com/qq_35379989/article/details/102726614
• 无人机中的 IMU 单元（MEMS 三轴加速计、三轴陀螺仪、三轴磁力计）_重力计和三轴加速度计区别-优快云 博客
  https://guoqing.blog.youkuaiyun.com/article/details/104598337
• IMU(陀螺仪、加速度计)&Magnetometer(磁力计) 校准方法和流程_imu 校准-优快云 博客
  https://blog.youkuaiyun.com/wuwuku123/article/details/105540349
• 【传感器】IMU (加速度计 + 陀螺仪)PI 数据融合以及结算四元数并求解欧拉角_imu 四元数的定义世界坐标系-优快云 博客
  https://blog.youkuaiyun.com/weixin_44410512/article/details/121950016
• 感知定位篇之 IMU:陀螺仪和加速度计及互补滤波_imu 传感器-优快云 博客
  https://blog.youkuaiyun.com/qq_60513199/article/details/137801025