数学定义误用 | 数学概念命名对学生常见错误的影响

注：本文为 “数学定义误用” 相关文章及讨论合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

Surprises from Mathematics Education Research: Student (Mis) use of Mathematical Definitions

数学教育研究中的意外发现：学生对数学定义的（误）使用

Author (s): Barbara S. Edwards and Michael B. Ward
Reviewed work (s):
Source: The American Mathematical Monthly, Vol. 111, No. 5 (May, 2004), pp. 411-424
Published by: Mathematical Association of America
Stable URL: https://www.jstor.org/stable/4145268
Accessed: 25/06/2012 12:31

1. INTRODUCTION

1. 引言

The authors of this paper met at a summer institute sponsored by the Oregon Collaborative for Excellence in the Preparation of Teachers (OCEPT). Edwards is a researcher in undergraduate mathematics education. Ward, a pure mathematician teaching at an undergraduate institution, had had little exposure to mathematics education research prior to the OCEPT program. At the institute, Edwards described to Ward the results of her Ph.D. dissertation [5] on student understanding and use of definitions in undergraduate real analysis. In that study, tasks involving the definitions of “limit” and “continuity,” for example, were problematic for some of the students. Ward’s intuitive reaction was that those words were “loaded” with connotations from their nonmathematical use and from their less than completely rigorous use in elementary calculus. He said, “I’ll bet students have less difficulty or, at least, different difficulties with definitions in abstract algebra. The words there, like ‘group’ and ‘coset,’ are not so loaded.”
本文作者在俄勒冈教师培养卓越合作项目（Oregon Collaborative for Excellence in the Preparation of Teachers, OCEPT）赞助的暑期研讨会上相识。爱德华兹是本科数学教育领域的研究者。沃德是一名纯数学家，任职于某本科院校，在参与 OCEPT 项目前几乎未接触过数学教育研究。研讨会上，爱德华兹向沃德介绍了她的博士论文成果 [5]，该论文聚焦本科实分析课程中学生对定义的理解与使用情况。在这项研究中，涉及 “极限”（limit）和 “连续性”（continuity）等定义的任务对部分学生构成了挑战。沃德的直观反应是，这些词汇在非数学语境中的含义，以及在初等微积分中不够严谨的使用，使其带有 “多重隐含意义”。他表示：“我敢打赌，学生在抽象代数中的定义学习上遇到的困难会更少，或者至少是不同类型的困难。抽象代数中的词汇，比如‘群’（group）和‘陪集’（coset），就没有这么多隐含意义。”

Eventually, with OCEPT support, the authors studied student understanding and use of definitions in an introductory abstract algebra course populated by undergraduate mathematics majors and taught by Ward. The “surprises” in the title are outcomes that surprised Ward, among others. He was surprised to see his algebra students having difficulties very similar to those of Edwards’s analysis students. (So he lost his bet.) In particular, he was surprised to see difficulties arising from the students’ understanding of the very nature of mathematical definitions, not just from the content of the definitions. Upon hearing of Edwards’s dissertation work, some other mathematicians who teach undergraduates found those difficulties surprising even when restricted to real analysis.
最终，在 OCEPT 的支持下，作者们对一门由沃德授课、面向数学专业本科生的抽象代数入门课程展开研究，探讨学生对定义的理解与使用情况。标题中的 “意外发现” 指的是让沃德等人感到意外的研究结果。他没想到自己教授的代数专业学生，会遇到与爱德华兹的实分析专业学生极为相似的困难（因此他输掉了赌注）。尤其让他意外的是，这些困难并非仅源于定义的内容本身，更源于学生对数学定义本质的理解不足。一些教授本科生的数学家在听闻爱德华兹的论文研究后，即便仅针对实分析领域的情况，也对学生存在的这些困难感到意外。

Hereafter, we present a simple two-part theoretical framework borrowed from philosophy and from mathematics education literature. Although it is not our intent to give an extensive report of either study, we next indicate the methodology used in Edwards’s dissertation and in our joint abstract algebra study so that the reader may know the context from which our observations are drawn. We then list the “surprising” difficulties of the two groups of students, documenting them with examples from the studies and using the framework to provide a possible explanation for them. We conclude with what we see as the implications for undergraduate teaching, along with some specific classroom activities that the studies and our experience as teachers suggest might be of value.
下文将介绍一个源于哲学和数学教育文献的两部分简单理论框架。尽管我们无意对两项研究进行详尽阐述，但接下来会说明爱德华兹博士论文及双方联合开展的抽象代数研究中所采用的研究方法，以便读者了解研究观察的背景。随后，我们将列出两组学生面临的 “意外” 困难，结合研究中的实例进行说明，并借助该理论框架给出可能的解释。最后，我们将阐述这些研究结果对本科教学的启示，以及结合研究和教学经验提出的一些有价值的具体课堂活动。

2. FRAMEWORK

2. 理论框架

It is commonly noted in mathematics departments that undergraduate mathematics majors often experience difficulties when trying to write mathematical proofs in their introductory abstract algebra, real analysis, or number theory courses. Some researchers have investigated certain aspects of students’ understanding or success in proof-writing [8], [16], [11]. In particular, Moore [11] notes that, while attempting to write formal proofs, students do not necessarily understand the content of relevant definitions or how to use these definitions in proof-writing. Edwards’s study with real analysis students [5] found that some undergraduate mathematics majors, even those who would be deemed successful based upon their grades, had difficulties understanding the role that mathematical definitions play in mathematics in general. There were particular difficulties in understanding the philosophical categorization of mathematical definitions and in using definitions to perform mathematical tasks, such as proving theorems.
数学系普遍观察到，数学专业本科生在抽象代数入门、实分析或数论课程中尝试撰写数学证明时，往往会遇到困难。部分研究者已针对学生在证明撰写中的理解情况或成功率的相关方面展开研究 [8]、[16]、[11]。尤其是穆尔（Moore）[11] 指出，学生在尝试撰写形式化证明时，未必理解相关定义的内容，也未必知晓如何在证明中运用这些定义。爱德华兹针对实分析专业学生的研究 [5] 发现，部分数学专业本科生（即便那些根据成绩被认为表现优秀的学生），在理解数学定义在数学学科中的整体作用方面存在困难。他们在理解数学定义的哲学分类，以及运用定义完成定理证明等数学任务时，面临的困难尤为突出。

Definitions play a key role in mathematics, but their creation and use differ from those of “everyday language” definitions. First, we turn to philosophers and lexicographers for useful categorizations and observations about definitions. Afterward, we look to mathematics education literature for some insights on the use of mathematical definitions.
定义在数学中扮演着关键角色，但其创建与使用方式与 “日常语言” 中的定义有所不同。首先，我们借鉴哲学家和词典编纂者对定义的有益分类与见解。随后，从数学教育文献中探寻关于数学定义使用的相关启示。

Philosopher Richard Robinson [15] distinguishes between lexical and stipulative definitions. Robinson writes “Lexical definition is that sort of word-thing definition in which we are explaining the actual way in which some actual word has been used by some actual person” [15, p. 35]. Lexicographer Sidney I. Landau [10] discusses the same category, but uses the term extracted definitions in place of lexical definitions because they are “definitions that are based on examples of actual usage, definitions extracted from a body of evidence” [10, p. 165]. Herein, we follow Landau’s terminology since Edwards used “lexical” in a different way in her earlier work.
哲学家理查德・罗宾逊（Richard Robinson）[15] 将定义分为词汇定义（lexical definitions）和规定性定义（stipulative definitions）两类。罗宾逊写道：“词汇定义是一种词 - 物对应定义，用于解释某个实际词汇被某些人实际使用的方式”[15, 第 35 页]。词典编纂者西德尼・I・兰道（Sidney I. Landau）[10] 也讨论了同一类别，但用 “提取性定义”（extracted definitions）替代了 “词汇定义”，因为这类定义 “基于实际使用案例，是从大量实例中提取而来的”[10, 第 165 页]。本文将采用兰道的术语，因为爱德华兹在其早期研究中对 “lexical” 的使用方式有所不同。

By contrast, Robinson uses stipulative definition to “mean the explicit and self-conscious setting up of the meaning-relation between some word and some object, the act of assigning an object to a name (or a name to an object)” [15, p. 59]. Its chief advantage is “the improvement of concepts or the creation of new concepts, which is the key to one of the two or three locks on the door of successful science” [15, p. 68]. Landau says such definitions “are imposed on the basis of expert advice” with the goal of “ease and accuracy of communication between those versed in the language of science” [10, p. 165].
相比之下，罗宾逊将规定性定义（stipulative definition）定义为 “明确且有意识地建立某个词汇与某个对象之间的意义关联，即给对象赋予名称（或给名称赋予对象）的行为”[15, 第 59 页]。其主要优势在于 “完善概念或创造新概念，这是打开成功科学大门的两三把钥匙之一”[15, 第 68 页]。兰道表示，这类定义 “基于专家建议而制定”，目的是 “让精通科学语言的人之间能够便捷、准确地沟通”[10, 第 165 页]。

Thus, extracted definitions report usage, while stipulated definitions create usage, indeed create concepts, by decree. Moreover, when a term is defined by stipulation, it is to be free from connotation, that is, free from all the associations the term may have acquired in its nontechnical use. We think of mathematical definitions as stipulated, whereas most “everyday language” definitions are extracted.
因此，提取性定义是对用法的描述，而规定性定义则是通过明确规定来创造用法，甚至创造新概念。此外，当一个术语通过规定性方式定义时，它应摆脱隐含意义，即不受该术语在非技术语境中可能获得的所有关联含义的影响。我们认为数学定义属于规定性定义，而大多数 “日常语言” 定义属于提取性定义。

We turn next to the mathematics education literature to describe how students use definitions in mathematics. According to Vinner [21] and Tall [19], each mathematical concept has associated with it a concept definition and concept image.1 The concept definition can be the stipulated definition assigned to a given concept. The concept image, on the other hand, is a nonverbal representation of an individual’s understanding of a concept. It includes the “visual representations, the mental pictures, the impressions and the experiences associated with the concept name” [21, p. 68]. We agree with Vinner in believing that mathematics instructors generally would imagine their students’ concept image as growing out of a given concept definition, as illustrated in the simple diagram of Figure 1.
接下来，我们结合数学教育文献，描述学生在数学中对定义的使用情况。根据文纳（Vinner）[21] 和托尔（Tall）[19] 的观点，每个数学概念都关联着一个概念定义（concept definition）和一个概念意象（concept image）¹。概念定义可以是为特定概念设定的规定性定义。而概念意象则是个体对概念理解的非语言表征，包括 “与概念名称相关的视觉表征、心理图像、印象和经验”[21, 第 68 页]。我们认同文纳的观点，即数学教师通常会认为学生的概念意象是基于给定的概念定义形成的，如图 1 中的简单示意图所示。

1 Our brief summary is based on our interpretation of Vinner [21], where the interested reader will find a more complete exposition.
¹ 本简要概述基于我们对文纳 [21] 相关研究的解读，感兴趣的读者可查阅该文献以获取更完整的阐述。

When faced with a task involving a concept, rigorous mathematics demands that concept usage follow one of the schemes charted by Vinner in Figures 2-4. The tasks we have in mind, for example, are proving theorems or identifying an object as having a certain defined structure, such as being a group. The key element is that in whatever ways the concept image enters into the processing and completion of the task, the ultimate output will be based solely on the concept definition.
当面对涉及某一概念的任务时，严谨的数学要求对概念的使用需遵循文纳在图 2-4 中所描绘的方案之一。我们所指的任务包括定理证明，或判断某个对象是否具有特定的定义结构（如是否为群）等。核心要点在于，无论概念意象以何种方式参与任务的处理与完成，最终结果都必须完全基于概念定义。

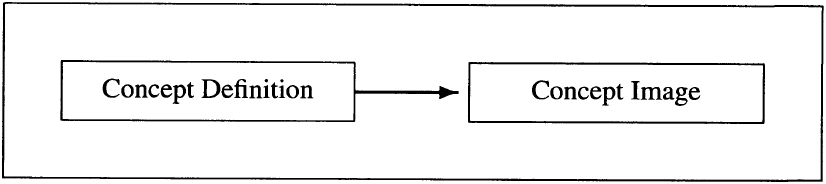
Figure 1. The idealized development of a formal mathematical concept [21].
图 1. 形式化数学概念的理想化形成过程 [21]。
（Concept Definition → Concept Image，即 “概念定义→概念意象”）

Figure 2. Interplay between definition and image [21].
图 2. 定义与意象的相互作用 [21]。
（Input → Concept Definition + Concept Image → Output，即 “输入→概念定义 + 概念意象→输出”）

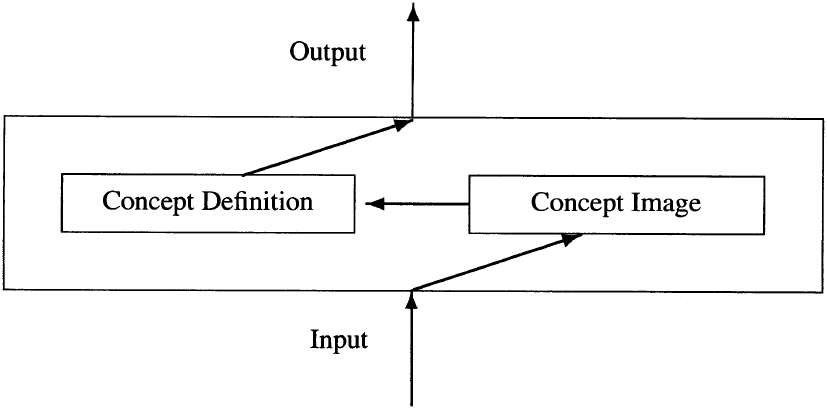
Figure 3. Deduction following intuitive thought [21].
图 3. 基于直觉思维的推理 [21]。
（Input → Concept Image → Concept Definition → Output，即 “输入→概念意象→概念定义→输出”）

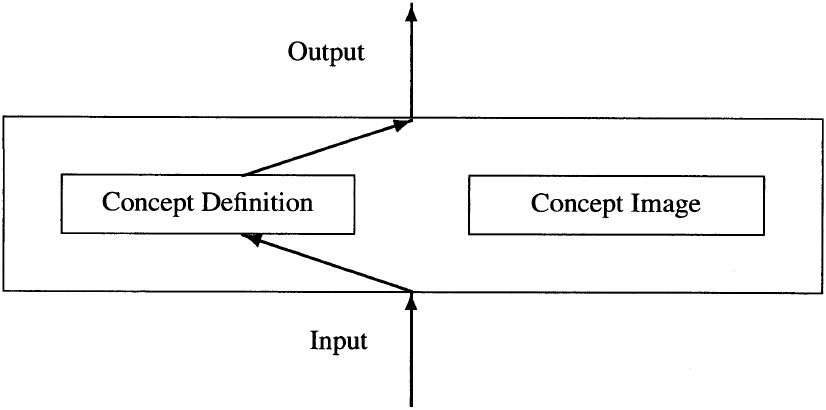
Figure 4. Purely formal deduction [21].
图 4. 纯形式化推理 [21]。
（Input → Concept Definition → Output，即 “输入→概念定义→输出”）

To summarize, we have introduced the categories of stipulated definitions, to which mathematical definitions belong, and extracted definitions. We have also provided cognitive models, based on concept definition and concept image, of some aspects of the processes by which definitions are used in the completion of mathematical tasks.
综上所述，我们介绍了规定性定义（数学定义所属类别）和提取性定义这两类定义。同时，基于概念定义和概念意象，我们提出了在完成数学任务过程中定义使用相关环节的认知模型。

3. METHODOLOGY

3. 研究方法

The purpose of both studies was to look beneath student understanding of the content of mathematical definitions to discern their understandings of the role played by formal definitions in mathematics. This is somewhat tricky since it is possible that a student might apply a definition in a mathematically incorrect way for at least two reasons. It could be an incomplete or faulty understanding of the concept that it defines. On the other hand, it could be a mathematically incorrect understanding of the role of mathematical definitions in general. A further difficulty influencing the design of these studies arose from the possibility that, if asked directly, students might profess a seemingly adequate understanding of the role of formal definitions in mathematics without really understanding this role. It is not uncommon for students (or any person for that matter) to repeat something they have heard without full understanding. For instance, students may say, perhaps to please instructors, that “mathematics is necessary in all walks of life,” without being able to give one meaningful example beyond the day-to-day interactions involved in commerce.
两项研究的目的均是深入探究学生对数学定义内容的理解，进而揭示他们对形式化定义在数学中所扮演角色的认知。这一研究目标颇具挑战性，因为学生以数学上不正确的方式运用定义可能源于至少两种原因：一是对定义所阐释的概念本身理解不完整或存在偏差；二是对数学定义在整体数学体系中的作用存在数学层面的错误认知。此外，研究设计还面临另一项困难：若直接询问学生，他们可能会声称自己充分理解形式化定义在数学中的作用，但实际上并未真正掌握。学生（或任何人）常常会重复一些自己并未完全理解的内容，这种情况并不罕见。例如，学生可能为了取悦教师而表示 “数学在各行各业中都不可或缺”，但除了日常商业交易中的简单应用外，他们无法给出任何有意义的例子。

Both studies employed similar research methods. For the methodology of the real analysis study see [5] and [6]. In the algebra study, the participants were enrolled in an “Introduction to Group Theory” course taught by Ward and observed by Edwards. Data for the study were in the form of two written class assignments² in which all fourteen students participated and interviews with eight student volunteers from the class. Each of these eight students participated in two one-hour task-based interviews (see the appendix). The first interview began with the question “What is mathematics?” By asking follow-up questions as needed, the interviewer made sure each student said something about the nature and role of definitions in mathematics. In both interviews students were asked to read a set of definitions that either had been or were to be introduced in their class, after which they were asked to work on a task related to the given definitions. We chose the definitions and tasks in an attempt to create situations in which students might have a conflict between their concept image and the concept definitions. We also selected definitions and tasks that our experience suggested would be difficult for the students. Our particular interest was to observe whether and, if so, how the students used the definitions in overcoming their difficulties. Students had access to the written definitions at all times during the interview. The interviews were audio-taped and video-taped. Verbatim transcripts of the interviews were made and analyzed.
两项研究采用了相似的研究方法。实分析研究的具体方法详见 [5] 和 [6]。在代数研究中，参与者是沃德授课、爱德华兹观察的 “群论入门” 课程的学生。研究数据包括两项所有 14 名学生均参与的书面课堂作业 ²，以及对该班级 8 名自愿参与学生的访谈记录。这 8 名学生每人参与了两次时长为一小时的任务型访谈（详见附录）。第一次访谈以 “数学是什么？” 这一问题开篇，访谈者通过必要的追问，确保每位学生都能谈及数学定义的本质与作用。在两次访谈中，学生均需阅读一组已在课堂上介绍过或即将介绍的定义，随后完成与这些定义相关的任务。我们对定义和任务的选择，旨在构建能让学生的概念意象与概念定义产生冲突的情境，同时也选取了根据教学经验判断对学生具有挑战性的定义和任务。我们尤为关注的是观察学生是否会运用定义来克服困难，以及若运用的话，具体如何运用。访谈过程中，学生可随时查阅书面定义。访谈全程进行了录音和录像，并形成逐字转录文本以供分析。

2 The written exercises are not discussed in this paper.
² 本文暂不讨论这些书面作业。

Analysis of the interview transcripts involved the following process. Independently, we read and reread the transcripts, studied the students’ written responses, and did an initial categorization based upon an interpretation of each student’s expressed view on the role of mathematical definitions and his or her mathematical behavior while working on the given tasks. We wrote brief case studies for each of the eight students and then met to compare our initial findings. We discussed our findings for each student and came to an agreement on a coding scheme to use for further study. Working individually, we then reread the transcripts using our coding scheme and met several times after this to discuss and refine our conclusions about each student. It was from comparing these results with each other and with Edwards’s dissertation conclusions that the surprises emerged.
访谈文本的分析过程如下：我们首先独立反复阅读转录文本，研究学生的书面作答情况，并根据每位学生对数学定义作用的表述以及完成任务时的数学行为，进行初步分类。随后，我们为这 8 名学生分别撰写了简要的案例分析报告，并共同讨论对比初步研究结果，就后续研究采用的编码方案达成一致。之后，我们各自运用该编码方案重新研读转录文本，并多次会面讨论、完善对每位学生的结论。正是通过对比这些研究结果以及爱德华兹的博士论文结论，我们得出了那些 “意外发现”。

4. THE SURPRISES

4. 意外发现

Surprise 1: Many students do not categorize mathematical definitions the way mathematicians do.

意外发现 1：许多学生对数学定义的分类方式与数学家不同

Mathematicians understand (and would be hard pressed to remember a time when they did not understand) that mathematical definitions are stipulated. As Robinson puts it [15, p. 59]:
数学家们清楚（且很难回忆起自己曾经不清楚的时刻），数学定义属于规定性定义。正如罗宾逊所表述的 [15, 第 59 页]：

Above all, the mathematicians, ever since Euclid at latest, have been making their own meanings for words. ‘By a denumerable series’, they say, for example, ‘we shall mean a series which you can put into one-to-one correspondence with the positive integers without changing its order.’ This is not a historical description of what has been meant by ‘denumerable’ in the past or is commonly meant by it now. It is an announcement of what is going to be meant by it in the present work, or a request to the reader to take it in that sense.
“最重要的是，至少从欧几里得时代起，数学家们就一直在为词汇赋予自己的含义。例如，他们会说‘所谓可数级数（denumerable series），是指可以在不改变顺序的情况下与正整数建立一一对应的级数’。这并非对‘可数’一词过去含义或当下普遍含义的历史描述，而是宣布该词在本文中的特定含义，或要求读者以此含义理解该词。”

Mathematics instructors may not be aware that some students do not categorize mathematical definitions among stipulated definitions. Indeed, this study came about by Ward betting Edwards that students in abstract algebra would have no choice but to treat the definitions as stipulated. To illustrate how some students fail to place mathematical definitions firmly in the stipulated category, we cite two examples from our abstract algebra study and one from Edwards’s dissertation study.
数学教师可能并未意识到，部分学生并未将数学定义归为规定性定义。事实上，本研究的开展源于沃德与爱德华兹的一个赌注 —— 沃德认为抽象代数专业的学生别无选择，只能将定义视为规定性定义。为说明部分学生未能明确将数学定义归入规定性定义类别，我们列举两个来自抽象代数研究的例子和一个来自爱德华兹博士论文研究的例子。

Asked “What is mathematics?” in the first interview of the abstract algebra study, Andre³ brought up the notions of theorem and definition. He said, “That is basically what a theorem is, a definition… Once [a theorem] is proven, it becomes a definition … At some point in time, we proved that 1 plus 1 is 2. Therefore, the definition is that always 1 plus 1 equals 2…” At first, Andre’s response seemed so strange that we were tempted to regard it as an outlier. However, by thinking in terms of the categorization of definitions, one can explain Andre’s point of view. For Andre, mathematical definitions reported facts. Andre was a student for whom all properties of a mathematical object held “by definition.” His definitions were extracted, though not from common usage, but rather from the body of knowledge about the concept. They were not stipulative in any sense.
在抽象代数研究的第一次访谈中，当被问及 “数学是什么？” 时，安德烈（Andre）³ 提到了定理和定义的概念。他说：“定理本质上就是一种定义…… 一旦（定理）被证明，它就成了定义…… 在某个时刻，我们证明了 1 加 1 等于 2，因此，定义就是 1 加 1 永远等于 2……” 起初，安德烈的回答显得十分特殊，我们险些将其视为特例。但从定义分类的角度来看，他的观点是可以解释的。对安德烈而言，数学定义是对事实的描述。在他看来，数学对象的所有性质都是 “根据定义” 成立的。他所理解的定义是提取性的，但并非源于日常用法，而是源于与概念相关的知识体系，绝非规定性定义。

3 All student names are pseudonyms.
³ 所有学生姓名均为化名。

Heidi, another student in the algebra study, provides another example of a student who seemed not to categorize mathematical definitions the way mathematicians do. However, she seemed to teeter on the cusp of understanding. We see her case as evidence that a student’s understanding of the categorization of mathematical definitions is not necessarily clear cut. Students do not fit nicely into one group (those who understand) or the other (those who do not understand). We think of this as a transition stage similar to what Burger and Shaughnessy [4] describe as transition stages of students understanding between van Hiele levels in geometry. According to Burger and Shaughnessy, it is possible that students may exhibit different levels of understanding on different tasks and some may even oscillate between levels of understanding on the same task.
海蒂（Heidi）是代数研究中的另一名学生，她的情况也表明部分学生对数学定义的分类方式与数学家不同，但她似乎正处于理解的临界点。我们认为，她的案例证明学生对数学定义分类的理解并非非黑即白 —— 学生并非简单地分为 “理解组” 和 “不理解组”。这一阶段类似于伯格（Burger）和肖内西（Shaughnessy）[4] 所描述的学生在几何范・希尔（van Hiele）水平之间的过渡阶段。根据伯格和肖内西的研究，学生在不同任务中可能表现出不同的理解水平，部分学生甚至在同一任务中会在不同理解水平之间波动。

The depth of Heidi’s understanding of the role of mathematical definitions was unclear to us after analyzing statements she made in her first interview. Sometimes she seemed to be exhibiting a mathematically correct view of definitions, as when she talked about a hierarchy of definitions and axioms being used to prove theorems. But a few lines later she said, “You have to make the definitions from what something actually is.”
分析海蒂在第一次访谈中的表述后，我们难以确定她对数学定义作用的理解深度。有时她会表现出对定义的数学层面正确认知，例如她提到定义和公理的层级结构可用于证明定理。但紧接着她又表示：“定义必须基于事物的实际本质来制定。”

In her second interview, Heidi was presented (for the first time) with the definition for coset multiplication (see the appendix, Definition 4). Before the interview, the definition of coset had been discussed in class (appendix, Definition 2). Heidi had calculated cosets and had observed some of their properties as part of a classroom activity. Ward had proved the basic properties of cosets in lecture, and Heidi had probably done some homework on cosets. Before she could even begin dealing with the coset multiplication definition, which was what we wanted to observe, she had to calculate some cosets. Unfortunately, she could not calculate them. She worked unsuccessfully for more than twenty minutes. Edwards asked her why the definition of “coset,” which was in front of her, was not helping her find the cosets. She replied, “Because I know how to do it, because I did it…” In her struggles, she repeatedly made similar statements. She did not seem to read the definition until pointedly prompted to do so by the interviewer.
在第二次访谈中，海蒂（首次）接触到了陪集乘法的定义（见附录定义 4）。访谈前，课堂上已讨论过陪集的定义（附录定义 2），海蒂也在课堂活动中计算过陪集并观察了其部分性质。沃德在课堂上证明了陪集的基本性质，海蒂很可能也完成了相关家庭作业。然而，在开始处理我们想要观察的陪集乘法定义之前，她需要先计算一些陪集，但她却无法完成这一操作，尝试了 20 多分钟仍未成功。爱德华兹询问她为何面前的 “陪集” 定义无法帮助她计算陪集，她回答：“因为我知道该怎么做，我以前做过……” 在尝试过程中，她多次表达了类似的想法。直到访谈者明确提示，她才开始阅读定义。

Heidi’s insistence on trying to remember how to compute cosets rather than to look at the definition was, perhaps, partly explained by embarrassment or a feeling that by now she ought to know the definition. However, taking into consideration the ambiguity in her descriptions of definitions in her first interview, another factor appeared to be at work. Having seen repeated instances of cosets over a period of days, she may have believed the definition should no longer be needed. Having been repeatedly shown instances of a chair, one does not need a definition in order to build or sit in a chair. Heidi seemed to believe that mathematical objects could be defined in the same way and that, if necessary, she should have been able to extract the definition from the instances.
海蒂坚持尝试回忆陪集的计算方法而非查阅定义，部分原因可能是出于尴尬，或是认为自己现在理应掌握该定义。但结合她在第一次访谈中对定义描述的模糊性，另一个因素似乎也在起作用：经过数天对陪集实例的反复接触，她可能认为不再需要定义了。就像人们在多次见过椅子后，无需定义就能制作或使用椅子一样，海蒂似乎认为数学对象也可以通过这种方式定义，且必要时她能从实例中提取出定义。

Stephanie, a participant in Edwards’s dissertation study (whose case is also discussed in [6]), seemed to believe that mathematical definitions were more like extracted definitions than like stipulated definitions. Just as a lexicographer must document a word’s extracted usage before it becomes a dictionary entry, Stephanie said that, when a mathematician writes a definition, “you would have to like have your colleagues, like review it, make sure it’s legitimate and there’s no errors.”
斯蒂芬妮（Stephanie）是爱德华兹博士论文研究的参与者（其案例也在 [6] 中讨论），她似乎认为数学定义更接近提取性定义而非规定性定义。她表示，就像词典编纂者必须先记录某个词的实际使用情况，才能将其纳入词典条目一样，数学家在撰写定义时，“必须让同事审核，确保定义合理且无错误”。

Andre, Heidi, and Stephanie were competent students. In fact, two of them earned high grades in their mathematics courses. Nevertheless, they categorized mathematical definitions incorrectly. All of them experienced difficulties that could be explained partly by their failure to place mathematical definitions firmly in the stipulated category.
安德烈、海蒂和斯蒂芬妮都是能力不错的学生，事实上其中两人在数学课程中取得了优异成绩。然而，他们对数学定义的分类方式存在错误，且他们所面临的部分困难，正是源于未能明确将数学定义归入规定性定义类别。

The readers may now wish to think of their own experiences with student misuse of definitions and consider the role miscategorization may play in that misuse.
读者此刻或许可以结合自己遇到的学生误用定义的案例，思考分类错误在其中可能扮演的角色。

Surprise 2: Many students do not use definitions the way mathematicians do, even when the students can correctly state and explain the definitions.

意外发现 2：即便学生能正确陈述和解释定义，许多人仍未以数学家的方式运用定义

The improper use of definitions is not a surprise. In an extreme (but familiar) case, definitions are not used at all! Anyone who has ever taught an advanced mathematics course will have seen students complete tasks as in Figure 5. Vinner calls that the “Intuitive Response.” Most mathematics instructors would assume such a response occurs when the student does not know or does not understand the definition. Instructors generally assume that if a student can accurately state and explain a definition, then victory is at hand and such purely intuitive responses will be banished, as will other misuses of definitions. Our data, alas, suggests otherwise. That is a surprise.
定义的不当使用并非意外。在极端（但常见）的情况下，学生甚至完全不使用定义！任何教授过高等数学课程的教师都见过学生以图 5 所示的方式完成任务。文纳将这种方式称为 “直觉反应”（Intuitive Response）。大多数数学教师会认为，这种反应源于学生不知道或不理解定义。教师通常假设，若学生能准确陈述并解释定义，就意味着问题已解决，这种纯直觉反应及其他定义误用情况都会消失。但遗憾的是，我们的数据表明事实并非如此 —— 这正是意外之处。

For example, in Edwards’s study, Stephanie was able to explain the definition of infinite decimal given in her real analysis course.⁴ She could use the definition to explain why $0.333\cdots =1/3$ (see [6] for details). Nevertheless, she disregarded the definition when she argued that $0.999\cdots$ was not equal to one. Instead, she used her concept image, which was based on long division. One can get $0.333\cdots$ by dividing 1 by 3, she said, but one does not get $0.999\cdots$ by dividing 1 by 1. The definition in front of her was ignored. When the concept definition conflicted with her concept image, the concept image won. Consistent with her categorization of mathematical definitions, she seemed to think the concept definition for repeating decimal had not been extracted quite correctly in the case of $0.999\cdots$.
例如，在爱德华兹的研究中，斯蒂芬妮能够解释实分析课程中给出的无限小数（infinite decimal）定义⁴。她能运用该定义解释为何 $0.333\cdots =1/3$（详见 [6]）。然而，当论证 $0.999\cdots$ 不等于 1 时，她却忽视了这一定义，转而依赖基于长除法形成的概念意象。她说，1 除以 3 能得到 $0.333\cdots$，但 1 除以 1 无法得到 $0.999\cdots$，完全忽略了面前的定义。当概念定义与概念意象发生冲突时，概念意象占据了主导地位。这与她对数学定义的分类认知一致 —— 她似乎认为，在 $0.999\cdots$ 这一案例中，循环小数的概念定义并未被正确提取。

4 The definition was: Let $c_1,c_2,...,c_n,...$ be an infinite sequence of integers with $0\le c_i\le 9$. The number sup ⁡ { 0. c 1 c 2 ⋯ c n ∣ n = 1 , 2 , 3 , . . . } \sup \{0.c_{1} c_{2}\cdots c_{n} | n=1,2,3, ...\} sup{0.c1​c2​⋯cn​∣n=1,2,3,...} is denoted by $0.c_1{c}_2\cdots c_n\cdots$ and is called an infinite decimal.
⁴ 该定义为：设 $c_1,c_2,...,c_n,...$ 为一整数序列，且满足 $0\le c_i\le 9$。数 sup ⁡ { 0. c 1 c 2 ⋯ c n ∣ n = 1 , 2 , 3 , . . . } \sup \{0.c_{1} c_{2}\cdots c_{n} | n=1,2,3, ...\} sup{0.c1​c2​⋯cn​∣n=1,2,3,...} 记为 $0.c_1{c}_2\cdots c_n\cdots$，称为无限小数。

Similarly, in the same study, Jesse gave an acceptable definition of continuity, yet used his concept image in claiming the absolute value function is not continuous at 0. Even though he kept saying that according to the definition the function should have been continuous, in the end, he placed more value on a memory from his introductory calculus course that something was “different” about the absolute value function.
同样在这项研究中，杰西（Jesse）能给出连续性的合理定义，但在声称绝对值函数在 0 点不连续时，却依赖了自己的概念意象。尽管他一再表示根据定义该函数应该是连续的，但最终还是更倾向于初等微积分课程中的记忆 —— 绝对值函数在 0 点 “有所不同”。

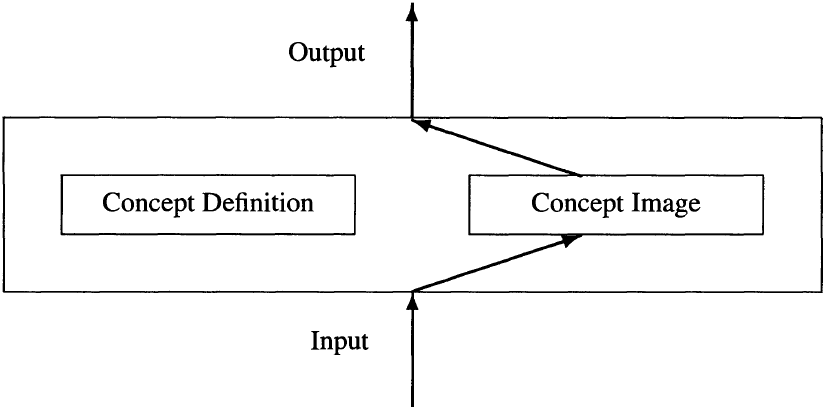
Figure 5. Intuitive response [21].
图 5. 直觉反应 [21]。
（Input → Concept Image → Output，即 “输入→概念意象→输出”）

Surprise 3: Many students do not use definitions the way mathematicians do, even in the apparent absence of any other course of action.

意外发现 3：即便看似别无选择，许多学生仍未以数学家的方式运用定义

Vinner writes, “It seems to us that many teachers at the secondary and the collegiate levels expect a one way process for the concept formation as shown in Figure 1, namely, they expect that the concept image will be formed by means of the concept definition and will be completely controlled by it” [21, p. 71]. That was certainly what Ward thought. He had no doubt about it in the case where the definition is simply a formula, as for coset multiplication (appendix, Definition 4). He had little doubt about it in general for a first course in abstract algebra, for terms like “group” and “ring” therein defined certainly could carry no connotation on which to build a concept image independent of the definition. He attributed the difficulties of Stephanie and Jesse to entrenched, flawed concept images formed by prior experience with repeating decimals and continuity. In the absence of any prior experience, Ward expected the interviews for the algebra study to show a concept image being formed and controlled by the concept definition. There seemed to be no alternative.
文纳写道：“在我们看来，许多中学和大学教师都期望概念形成过程是单向的，如图 1 所示，即概念意象通过概念定义形成，并完全受其控制”[21, 第 71 页]。沃德对此深表认同。对于像陪集乘法这样仅以公式形式呈现的定义（附录定义 4），他毫不怀疑这一点。对于抽象代数入门课程中的一般术语（如 “群” 和 “环”），他也几乎没有疑问 —— 这些术语的定义显然不会带有独立于定义本身的隐含意义，因此无法形成脱离定义的概念意象。他将斯蒂芬妮和杰西的困难归因于：他们此前对循环小数和连续性的学习经验，形成了根深蒂固且存在偏差的概念意象。而在学生缺乏相关先验经验的情况下，沃德期望代数研究的访谈结果能证明，概念意象是基于概念定义形成并受其控制的 —— 似乎除此之外别无可能。

We selected the definition of coset multiplication for use in our second interview because it is a known trouble maker in group theory. Some sources of the trouble have been studied in [3] and [2]. For students who might not have difficulty with the content of the definition, we ensured trouble of another kind by asking the students to consider a situation in which coset multiplication was not well-defined. Whatever the source of the trouble, our particular interest was in observing whether and, if so, how the students used definitions as tools in dealing with the trouble.
我们选择在第二次访谈中使用陪集乘法的定义，是因为它是群论中公认的难点。部分相关难点来源已在 [3] 和 [2] 中进行了研究。对于那些可能在定义内容理解上无困难的学生，我们通过设置陪集乘法不满足良定义的情境，人为制造了另一类挑战。无论困难源于何处，我们尤为关注的是观察学生是否会将定义作为工具来应对困难，以及具体如何运用。

Heidi, after finally calculating the necessary cosets, read the definition of coset multiplication and said, “Would you do it like in a FOIL form… ?” FOIL, First-Outer-Inner-Last, refers to the distributive property for multiplying two binomials. Here it amounts to elementwise multiplication of the two cosets. (Ironically, in some cases, Heidi’s scheme is actually equivalent to the given definition, a fact that is not entirely obvious.) Andre did a similar computation (under the moniker “Marvin the Martian” because the lines he drew to designate the products formed an alien-looking face).
海蒂在最终算出所需陪集后，阅读了陪集乘法的定义并问道：“是不是要用 FOIL 法则来计算……？”FOIL（First-Outer-Inner-Last，即首项 - 外项 - 内项 - 末项）指的是两个二项式相乘的分配律，在此处相当于对两个陪集进行元素级乘法运算。（颇具讽刺意味的是，在某些情况下，海蒂的方法与给定定义实际上是等价的，这一点并非显而易见。）安德烈也进行了类似的计算（他将其称为 “火星人马文法”，因为他为标记乘积而画的线条形成了一个类似外星人的面孔）。

Blake, another student in the algebra study, had a sophisticated understanding of the structure of mathematics. His description of the nature of mathematical definition was on target. In both interviews, he repeatedly sought answers in the given definitions, making comments like “It has got to be in this definition …” Nevertheless, realizing that the operands in coset multiplication are sets, he wondered for some time if the definition of coset multiplication was only a “weird way” to indicate “simply listing them [the coset elements] all out,” by which he meant forming the union of the two cosets. He then tried to imagine how the given formula might describe union.
布莱克（Blake）是代数研究中的另一名学生，他对数学结构有着深刻的理解，对数学定义本质的描述也十分准确。在两次访谈中，他多次从给定定义中寻找答案，发表诸如 “答案肯定在这个定义里……” 之类的言论。然而，当意识到陪集乘法的运算对象是集合时，他曾一度疑惑，陪集乘法的定义是否只是一种 “奇怪的表达方式”，实则是 “将陪集元素全部列出”（即求两个陪集的并集），并试图构想给定公式如何描述并集运算。

For Heidi and Andre, the coincidental fact that each coset in the problem we presented contained two elements led them to write expressions such as { V , H } { D , F } \{V, H\}\{D, F\} {V,H}{D,F}. Presumably, that cued the FOIL response because of the visual similarity with $(V+H)(D+F)$. For Blake, the fact that two sets were being operated together brought to mind another set operation, union. He then tried to imagine how the given formula might describe union. For all three students, the concept image for coset multiplication was not formed as envisioned in Figure 1, even though we conjectured there would be no alternative. Instead, we saw the appearance of an inappropriate, preexisting, concept image, namely, either FOIL or union. The inappropriate concept image competed with or may even have replaced the concept definition as the controlling force in the formation of the concept image (see Figure 6). Upon reading an unfamiliar mathematical definition, an experienced mathematician is more likely to form a concept image (at least a partial concept image) based solely on the concept definition and then afterward to explore its relationship to existing images. Heidi, Andre, and Blake did not use the concept definition in the way an experienced mathematician would use it.
在我们给出的问题中，每个陪集恰好包含两个元素，这一巧合让海蒂和安德烈写出了 { V , H } { D , F } \{V, H\}\{D, F\} {V,H}{D,F} 这类表达式。推测来看，这种表达式与 $(V+H)(D+F)$ 在视觉上的相似性，触发了他们对 FOIL 法则的联想。而对布莱克而言，两个集合进行运算这一事实，让他联想到了另一种集合运算 —— 并集。对于这三名学生而言，陪集乘法的概念意象并未如我们猜想的那样（如图 1 所示）形成，而是出现了不恰当的、预先存在的概念意象（即 FOIL 法则或并集运算）。这种不恰当的概念意象与概念定义竞争，甚至可能取代了概念定义，成为概念意象形成的主导因素（见图 6）。经验丰富的数学家在阅读不熟悉的数学定义时，更倾向于首先仅基于概念定义形成概念意象（至少是部分概念意象），随后再探究其与已有意象的关联。但海蒂、安德烈和布莱克并未以这种方式运用概念定义。

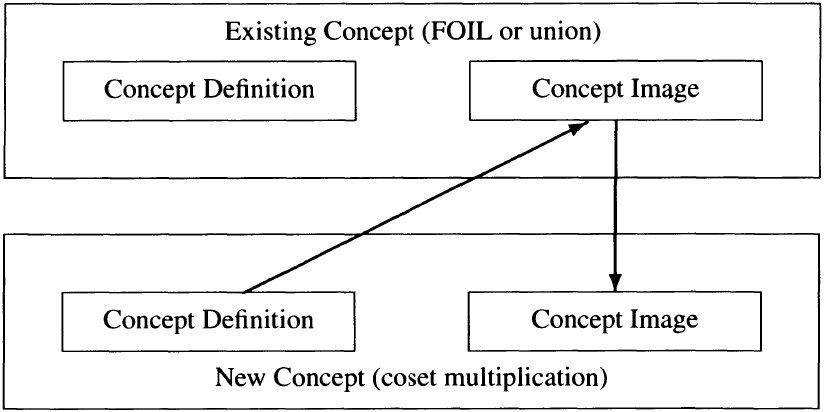
Figure 6. Inappropriate image influencing image formation.
图 6. 不恰当意象对意象形成的影响
（Existing Concept (FOIL or union) → Concept Definition → Concept Image (New Concept: coset multiplication)，即 “已有概念（FOIL 法则或并集）→概念定义→概念意象（新概念：陪集乘法）”）

5. IMPLICATIONS FOR TEACHING

5. 对教学的启示

In this section we give some implications for teaching inspired by these studies. We also suggest some sample classroom activities. Investigating the effectiveness of these suggestions could be the basis for future research.
本节将基于上述研究结果，提出一些对教学的启示，并推荐一些具体的课堂活动。这些建议的有效性可作为未来的研究方向。

Implication 1.

启示 1：
The special nature of mathematical definitions should be treated as a concept in its own right, one that should be understood at some level by all college mathematics students.
数学定义的特殊性应被视为一个独立概念，所有大学数学专业学生都应在一定程度上理解这一概念。

This is especially important in a student’s first proof-intensive course, which we refer to generically as an “introduction to proof” course. Certainly a case can be made for insisting that students know the exact content of the definitions they use, but this is not sufficient. It is very clear from our analysis of the data in these studies that students also need to understand the specific role definitions play in mathematics. Thus in such courses the nature of mathematical definitions needs to be addressed more directly and more often.
这一点在学生的第一门证明密集型课程（我们统称为 “证明入门” 课程）中尤为重要。固然，要求学生掌握所使用定义的具体内容是合理的，但这并不足够。我们对研究数据的分析明确表明，学生还需要理解定义在数学中所扮演的特定角色。因此，在这类课程中，需要更直接、更频繁地探讨数学定义的本质。

In particular, introduction to proof courses certainly should include a unit on the categorization and use of mathematical definitions. The introductory material in this article should be sufficient for describing the categorization of definitions, although reading chapter 4 of Robinson [15] for additional background would be very enlightening for the instructor. Chapter 3 in Solow [17] and chapter 3 (especially pages 82-83) in Exner [7] illustrate methods for teaching the use of mathematical definitions.
具体而言，证明入门课程应包含一个关于数学定义分类与使用的单元。本文的引言部分已足够说明定义的分类方式，不过教师阅读罗宾逊 [15] 的第 4 章以获取更多背景知识，将会大有裨益。索洛（Solow）[17] 的第 3 章和埃克斯纳（Exner）[7] 的第 3 章（尤其是第 82-83 页）介绍了数学定义使用的教学方法。

It may be informative for students (and instructors) to search the dictionary for words that have both extracted and stipulated definitions. For instance, The American Heritage Dictionary [1] lists both extracted and stipulative definitions for the word “radical,” namely, “excellent; wonderful” and “the root of a quantity as indicated by the radical sign,” respectively. This is an especially good example because it shows how the use of words over time can evolve new extracted definitions. The definition “excellent; wonderful” is not found in dictionaries printed thirty years ago. Mathematical definitions are not extracted from popular usage in the way “excellent” has become a definition for “radical.” Though mathematical definitions can vary over time and context, mathematicians are careful to stipulate which definitions are to be used in their own work.
让学生（和教师）查阅词典中同时具有提取性定义和规定性定义的词汇，可能会颇有启发。例如，《美国传统词典》（The American Heritage Dictionary）[1] 中 “radical” 一词就同时列出了这两类定义：提取性定义为 “极好的；绝妙的”，规定性定义为 “根号所表示的一个数的根”。这是一个尤为恰当的例子，因为它展示了词汇的用法如何随着时间推移演变出新的提取性定义 ——“极好的；绝妙的” 这一定义在 30 年前的词典中并未出现。数学定义并非像 “radical” 的 “极好的” 这一定义那样，从通俗用法中提取而来。尽管数学定义可能会随时间和语境变化，但数学家会明确规定自己研究中所使用的定义。

There are other available activities that focus on the nature of mathematical definitions. We give a few recommendations here.
还有其他一些聚焦于数学定义本质的课堂活动，以下推荐几个示例：

A short version of the junior high activity in [12] played out very well for Ward, even in an upper-division axiomatic geometry course. It quickly illustrates why mathematical definitions are and must be stipulated with such precision. The activity went as follows.
沃德在高年级公理几何课程中开展了 [12] 中一项初中活动的简化版本，效果极佳。该活动能快速说明为何数学定义需要且必须被如此精确地规定，具体过程如下：

• Question from Ward: What is a quadrilateral?
  沃德的问题：什么是四边形？

• Response from the class: A four-sided figure.
  全班学生的回答：四条边的图形。

• Ward drew a four-sided figure with curved sides.
  沃德画了一个四条边均为曲线的图形。

• Response: Oops, a four-sided figure having straight line segments as sides.
  学生回应：哦，是由直线段组成的四条边的图形。

• Ward drew an open four-sided figure …
  沃德画了一个不闭合的四条边图形……

The activity continued in this fashion until an acceptable definition was given. (Reference [12] gives further details and follow-up activities.)
活动以这种方式持续进行，直至学生给出可接受的定义（[12] 提供了更多细节和后续活动）。

Even more to the point are activities that engage students in actually formulating definitions in the same way that practicing mathematicians do. For example, Edwards uses David Henderson’s geometry text [9] in a course for mathematics majors who intend to teach either high school or community college mathematics. Early in the course students have a definition of “triangle” that is useful for a while on the Euclidean plane, on the sphere, and on the hyperbolic plane, even though triangles on the sphere can sometimes look a good deal different than the triangle on the plane that we have seen since elementary school. However, students eventually find that the Side-Angle-Side Theorem (SAS) is not true for all triangles on the sphere. At this point they must do what all mathematicians do—look for the special case or cases for which the theorem is valid. This leads to a special definition of a “small triangle,” one for which SAS is true on the sphere.
更具针对性的活动是让学生以执业数学家的方式亲自构建定义。例如，爱德华兹在一门面向未来将教授高中或社区大学数学的数学专业学生的课程中，使用了大卫・亨德森（David Henderson）的几何教材 [9]。课程初期，学生学习的 “三角形” 定义在欧几里得平面、球面和双曲面上均适用一段时间 —— 尽管球面上的三角形有时与我们从小学起就熟悉的平面三角形看起来大相径庭。但学生最终会发现，边角边定理（SAS）并非对球面上的所有三角形都成立。此时，他们必须像所有数学家那样，寻找该定理成立的特殊情况，进而得出 “小三角形” 的特殊定义 —— 在球面上，边角边定理对 “小三角形” 成立。

Implication 2.

启示 2：
Instructors can better understand the struggles undergraduate students face in proof-intensive courses by thinking in terms of the required shift to the concept definition-based logical reasoning illustrated in Figures 2-4. The students very likely have thirteen years of conditioning in courses where Vinner’s Intuitive Response (Figure 5) is closer to the norm. This transition can be difficult, not to mention puzzling, for many students.
教师可以通过图 2-4 所示的、基于概念定义的逻辑推理转变要求，更好地理解本科生在证明密集型课程中面临的困境。学生在之前的 13 年学习中，已习惯了以文纳的 “直觉反应”（图 5）为主导的课程模式，这种转变对许多学生而言既困难又令人困惑。

A brief presentation (like the one herein, for example) on concept definition and concept image might provide students with a framework in which to think about what is happening in their classes. In fact, Vinner’s discussion on concept definition and concept image [21, pp. 68-73] is probably accessible enough to be of value to an undergraduate. That presentation might be done in conjunction with a reading on the centrality of rigor and proof in mathematics such as is found in Stewart (“What Mathematics Is About” [18, chap. 3]) in order to explain why the shift to increased rigor is necessary.
简要介绍概念定义与概念意象（例如本文中的相关内容），可为学生提供一个框架，帮助他们理解课堂上的学习内容。事实上，文纳关于概念定义与概念意象的讨论 [21, 第 68-73 页] 通俗易懂，对本科生颇具价值。教师可结合一篇关于数学严谨性与证明核心地位的读物（如斯图尔特（Stewart）的《数学是什么》[18, 第 3 章]）进行讲解，以说明为何需要向更高严谨性转变。

Ward used the material from Vinner in two recent courses, an upper-division course in axiomatic geometry and an introduction to proof course. In geometry, he spent about twenty minutes on the first day of class discussing concept image versus concept definition and showing Figures 1-5. Most of the students immediately adopted Vinner’s terminology. When asking about a step in a proof, many would say “My concept image is… [usually referring to a diagram]. How do I make that rigorous?” When an unjustified claim was made in a proof (for example, “ABCD is a quadrilateral”), Ward would ask: “Is that based on concept image (the diagram) or concept definition (A, B, C, and D are distinct coplanar points, no three of which are collinear, and any pair of the segments AB, BC, CD, and DA either have no points in common or have only an endpoint in common)?” The students all seemed to see the point of such questions.
沃德在近期的两门课程（高年级公理几何和证明入门）中运用了文纳的相关内容。在几何课程中，他在第一堂课用了约 20 分钟时间，讨论概念意象与概念定义的区别，并展示了图 1-5。大多数学生很快就掌握了文纳的术语，在询问证明中的某个步骤时，许多学生会说 “我的概念意象是……（通常指图形），如何让它变得严谨？” 当证明中出现无依据的断言（例如 “ABCD 是四边形”）时，沃德会问道：“这一断言是基于概念意象（图形）还是概念定义（A、B、C、D 是共面的不同点，且无三点共线，线段 AB、BC、CD、DA 中的任意两条要么无公共点，要么仅有一个端点重合）？” 学生们似乎都能理解这类问题的意义。

In the introduction to proof course, Ward introduced the concept image/concept definition terminology and Vinner’s figures late in the course after several structural proof techniques (in the style of Velleman [20], Solow [17], or Exner [7, chap. 3]) had been introduced. He referred to various proofs done earlier in the course and showed how the diagrams modeled the process used in class to produce the proofs. For example, in proofs about sets, Venn diagrams provided a useful part of a concept image in some cases. Figure 2 or Figure 3 modeled the process by which those proofs were constructed. For proving injectivity and surjectivity of functions, Ward had stressed how a proof strategy could be outlined by simply looking at the quantifiers in the definitions. He then related that to Figure 4. For the students who continued to write heuristic, arm-waving pseudo-proofs, Ward pointed to Figure 5.
在证明入门课程中，沃德在介绍了多种结构化证明技巧（参考维勒曼（Velleman）[20]、索洛 [17] 或埃克斯纳 [7, 第 3 章] 的风格）后，于课程后期引入了概念意象 / 概念定义的术语及文纳的示意图。他回顾了课程前期的各类证明，展示了这些示意图如何模拟课堂上的证明构建过程。例如，在集合相关证明中，维恩图（Venn diagrams）在某些情况下是概念意象的重要组成部分，图 2 或图 3 可模拟这些证明的构建过程。在证明函数的单射性（injectivity）和满射性（surjectivity）时，沃德强调了如何仅通过分析定义中的量词来勾勒证明策略，并将其与图 4 关联起来。对于那些仍在撰写启发性、表述模糊的伪证明的学生，沃德则以图 5 为例进行说明。

Implication 3.

启示 3：

The results of this research should be considered in the mathematical preparation of future teachers.
未来教师的数学培养应纳入本研究结果。

One might ask if it is sufficient to wait until students are enrolled in post-calculus mathematics courses to begin talking about the special nature of mathematical definitions? In Edwards’s dissertation study with students in a beginning real analysis course, Jesse provided some evidence against waiting. Especially in Jesse’s early interviews, he displayed a belief (and even acted accordingly) that the words of a definition were secondary to one’s understanding of the related concept. To use the terminology of Vinner, if one’s concept image conflicted with the related concept definition, Jesse believed the concept image should prevail. Jesse repeatedly attributed his understanding of the nature of mathematical definitions to what he had learned in his high school mathematics courses. As he explained in the second interview, his AP calculus instructor had talked early in the course about the notion of formal mathematical definitions. But Jesse said, “After about the first day in calculus, we didn’t care about this [formal definition] if you had the concept right, not really the definition, that was all that really mattered.” And again in the third interview he said, “[the calculus teacher] would even say, now this [the formal definition] may mean a lot of jargon, but this is what it really means.” We can probably understand the motives of the instructor. It is important for students to have deep conceptual understandings. Jesse’s instructor probably did not want his students to be hindered by what often seems to be the heavily symbolic and terse language of formal definitions, but he was also assuming (or hoping?) that his students would not leave his course with mathematically incorrect understandings of the concepts in calculus.
有人可能会问，是否有必要等到学生进入微积分后续数学课程后，再开始探讨数学定义的特殊性？爱德华兹在针对实分析入门课程学生的博士论文研究中，杰西的案例提供了反对延迟的证据。尤其是在杰西的早期访谈中，他表现出一种信念（且据此行事）：定义的文字表述相对于对相关概念的理解而言是次要的。用文纳的术语来说，若概念意象与概念定义发生冲突，杰西认为概念意象应占主导地位。杰西多次表示，他对数学定义本质的理解源于高中数学课程。正如他在第二次访谈中所解释的，他的大学先修课程（AP）微积分教师在课程初期曾提及形式化数学定义的概念，但杰西说：“在微积分课程的第一天之后，我们就不再关注这个（形式化定义）了 —— 只要你理解了概念，定义并不重要，这才是关键。” 在第三次访谈中他又提到：“（微积分教师）甚至会说，这个（形式化定义）可能包含很多专业术语，但这才是它的真正含义。” 我们或许能理解这位教师的初衷：让学生形成深刻的概念理解至关重要。杰西的教师可能不希望学生被形式化定义中往往晦涩难懂的符号语言所阻碍，但他同时也假设（或希望？）学生在课程结束时，不会对微积分中的概念形成数学层面错误的理解。

The goal of helping students develop deep conceptual understandings does not have to conflict with helping students see the special role played by definition in mathematics. Indeed, The National Council of Teachers of Mathematics Standards recommend that “Teachers can help students see that some words that are used in everyday language, such as similar, factor, area, or function are used in mathematics with different or more-precise meanings. This observation is the foundation for understanding the concept of mathematical definition” [13, p. 63]. In other words, the standards advise K-12 mathematics teachers to inform students of the need to beware of connotations a word may carry because of its nontechnical use and also of the need to distinguish informal concept images from precise concept definitions.
帮助学生形成深刻的概念理解，与帮助他们认识到定义在数学中的特殊作用，这两个目标并非相互冲突。事实上，美国国家数学教师委员会（The National Council of Teachers of Mathematics）的标准建议：“教师应帮助学生认识到，一些日常语言中的词汇（如‘相似的’（similar）、‘因数’（factor）、‘面积’（area）或‘函数’（function））在数学中具有不同或更精确的含义。这一认知是理解数学定义概念的基础”[13, 第 63 页]。换句话说，该标准建议 K-12 数学教师告知学生：需警惕词汇在非技术语境中可能携带的隐含意义，同时需区分非正式的概念意象与精确的概念定义。

Furthermore, it is worth noting a common method of creating definitions that seems related to extracted definitions. One defines ostensively [15, pp. 117-126], [10, pp. 167-168] when one indicates something, with a gesture perhaps, and says “this is a…” With enough repetition, one expects the listener to pick up the meaning. Recall that Heidi seemed to be under the impression that cosets could be defined ostensively.
此外，值得注意的是一种常见的定义方式，它似乎与提取性定义相关，即实指定义（ostensive definition）[15, 第 117-126 页]、[10, 第 167-168 页]—— 通过手势等方式指向某个事物，并说 “这是一个……”。经过足够多次的重复，听者便能理解该词的含义。回想一下，海蒂似乎就认为陪集可以通过实指定义来界定。

Since many mathematics majors will eventually teach mathematics at some level, they should be made aware of the dangers of defining ostensively. Prevost reports on high school sophomores who were repeating a geometry course during the summer, having failed it the previous year. He writes, “Almost all the students could parrot the definitions they had learned during the previous year. Their ‘working definition,’ however, was ‘looks like.’ … As teachers, we are guilty of reinforcing this ‘looks like’ definition. The figures we draw are stereotypical and oriented with one side parallel to the lower edge of the paper or chalkboard” [14, p. 412]. Thus, for instance, a square whose sides are not parallel to the sides of the paper was identified by the students as “a diamond, perhaps, but not a square” [14, p. 411]. In the terminology of this paper, in spite of knowing the stipulated definitions of geometric figures, those students worked as though the figures had been defined ostensively by repeated reference to stereotypical instances of figures in certain orientations. They remained at van Hiele’s “recognition” level of geometric sophistication rather than advancing to the “analysis” level. (See [4] for a discussion of the van Hiele levels.) Not surprisingly, Prevost relates this failure at accurate identification to failure in the course.
由于许多数学专业学生最终会在不同层面教授数学，因此应让他们意识到实指定义的潜在风险。普雷沃斯特（Prevost）报告了一组高中二年级学生的情况，他们因前一年几何课程不及格，在暑期重修该课程。他写道：“几乎所有学生都能复述前一年学到的定义，但他们的‘工作定义’却是‘看起来像’…… 作为教师，我们对强化这种‘看起来像’的定义负有责任 —— 我们绘制的图形都是刻板的，且总有一条边与纸张或黑板的下边缘平行”[14, 第 412 页]。例如，学生们会将边不与纸张边缘平行的正方形识别为 “可能是菱形，但不是正方形”[14, 第 411 页]。用本文的术语来说，尽管这些学生知道几何图形的规定性定义，但他们的实际运用却表明，这些图形似乎是通过反复参考特定朝向的刻板实例而进行的实指定义。他们的几何认知仍停留在范・希尔的 “识别” 水平，未能进阶到 “分析” 水平（关于范・希尔水平的讨论详见 [4]）。不足为奇的是，普雷沃斯特将这种识别错误与课程不及格相关联。

We certainly are not calling for the use in K-14 classrooms of the so-called definition-theorem-proof means of discourse that is prevalent and valuable among working mathematicians. What we are saying is that teaching for conceptual understanding is valuable but should not be done at the expense of students’ building a good understanding of the nature and use of mathematical definitions. Even before students take proof-intensive courses and even before college, instructors should attempt to plant the seeds of a more rigorous approach to the use of definitions. Thus, it is particularly important that undergraduate mathematics students who plan to teach should have experiences in their college courses that help them build robust understandings of the role and use of mathematical definitions.
我们当然并非主张在 K-14 课堂中采用执业数学家之间普遍使用且颇具价值的 “定义 - 定理 - 证明” 式表述方式。我们的意思是，以概念理解为导向的教学固然重要，但不应以牺牲学生对数学定义本质与使用的良好理解为代价。甚至在学生进入大学、接触证明密集型课程之前，教师就应尝试埋下种子，让学生逐步形成更严谨的定义使用方式。因此，对于计划从事教学工作的本科数学专业学生而言，在大学课程中获得有助于他们深刻理解数学定义作用与使用方法的学习体验，尤为重要。

6. CONCLUSION

6. 结论

We have used terms from the literature on definitions to categorize definitions as extracted (everyday language) or stipulated (mathematical). Our research has shown that undergraduate mathematics majors may not fully understand this distinction, and that this failure to understand affects their understanding of the concepts themselves. The tendency of some of the real analysis students in Edwards’s original study to rely on their concept images instead of the related concept definitions, when the two were in conflict, could be partially explained by the fact that some of the definitions used in that study were for concepts that were very familiar to the students from their previous mathematics courses (continuity and infinite decimal, for example). This was not the case in the abstract algebra study, yet some of the algebra students displayed a similar preference for concept image over concept definition.
我们借鉴定义相关文献中的术语，将定义分为提取性定义（日常语言中的定义）和规定性定义（数学中的定义）。研究表明，本科数学专业学生可能并未完全理解这一区别，而这种理解不足会影响他们对概念本身的理解。在爱德华兹最初的实分析研究中，部分学生在概念意象与概念定义发生冲突时倾向于依赖概念意象，这一现象部分可归因于：该研究中使用的部分定义所涉及的概念（如连续性和无限小数），学生在之前的数学课程中已十分熟悉。而在抽象代数研究中，情况并非如此，但部分代数专业学生仍表现出类似的倾向 —— 更倾向于依赖概念意象而非概念定义。

We have concluded, therefore, that the special nature of mathematical definitions should be addressed more directly in mathematics courses at all levels, but especially in the first proof-intensive course. Students should have experiences that focus on the use of mathematical definitions and experiences in the process of defining. Although it may be true that many students eventually “figure out” the role of mathematical definitions, it seems that it would be preferable not to leave this important facet of the nature of mathematics to chance.
因此，我们得出结论：数学定义的特殊性应在各级数学课程中更直接地予以探讨，尤其是在第一门证明密集型课程中。学生应获得聚焦于数学定义使用的学习体验，以及参与定义构建过程的体验。尽管许多学生最终可能会 “领悟” 到数学定义的作用，但将数学本质中这一重要方面交由偶然因素决定，显然并非理想之举。我们希望本文提出的理论框架与实例，能为那些有意帮助学生更深入理解数学定义及其使用方法的教师提供一个起点。

7. APPENDIX

7. 附录

Abstract Algebra Interview 1

抽象代数访谈 1

The first interview began with Edwards asking “What is mathematics?” By asking follow-up questions as needed, Edwards made sure each student said something about the nature and role of definitions in mathematics.
第一次访谈以爱德华兹提出的 “数学是什么？” 开篇。通过必要的追问，爱德华兹确保每位学生都能谈及数学定义的本质与作用。

After that introductory discussion, each student was handed the following definition. Binary operations were being studied in class, but the definition of group had not yet been presented.
在这段引入性讨论之后，每位学生都收到了以下定义。当时课堂上正在学习二元运算，但尚未介绍群的定义。

Definition 1 Let $G$ be a nonempty set together with a binary operation that assigns to each ordered pair $(a,b)$ of elements of $G$ an element of $G$ denoted by $a\ast b$. We say $G$ is a group under $\ast$ if the following three properties are satisfied.
定义 1 设 $G$ 为非空集合，其上定义了一个二元运算：对 $G$ 中的任意有序元素对 $(a,b)$，该运算均对应 $G$ 中的一个元素，记为 $a\ast b$。若该运算满足以下三条性质，则称 $G$ 关于运算 $\ast$ 构成一个群（group）。

1. The operation $\ast$ is associative; that is, $(a\ast b)\ast c=a\ast (b\ast c)$ for all $a,b,c$ in $G$.
   运算 $\ast$ 满足结合律（associative），即对任意 $a,b,c\in G$，均有 $(a\ast b)\ast c=a\ast (b\ast c)$。

2. There is an element $e$ (called the identity) in $G$, such that $a\ast e=e\ast a=a$ for all $a$ in $G$.
   $G$ 中存在一个元素 $e$（称为单位元，identity），使得对任意 $a\in G$，均有 $a\ast e=e\ast a=a$。

3. For each element $a$ in $G$ there is an element $b$ in $G$ (called the inverse of $a$) such that $a\ast b=b\ast a=e$.
   对 $G$ 中的任意元素 $a$，均存在 $G$ 中的一个元素 $b$（称为 $a$ 的逆元，inverse of $a$），使得 $a\ast b=b\ast a=e$。

After reading the definition, each student was given these three tasks to complete.
阅读定义后，每位学生需完成以下三项任务：

1. Set: $\mathbb{R}$, the set of real numbers; Binary Operation: Ordinary subtraction, $-$; Is $\mathbb{R}$ a group under subtraction?
   集合：$\mathbb{R}$（实数集）；二元运算：普通减法 $-$；实数集 $\mathbb{R}$ 关于减法是否构成群？

2. Set: $\mathbb{R}$, the set of real numbers; Binary Operation: The operation $\oplus$ where $a\oplus b=a+b+3$; Is $\mathbb{R}$ a group under $\oplus$?
   集合：$\mathbb{R}$（实数集）；二元运算：运算 $\oplus$，其中 $a\oplus b=a+b+3$；实数集 $\mathbb{R}$ 关于运算 $\oplus$ 是否构成群？

3. Set: $\mathbb{R}$, the set of real numbers; Binary Operation: Ordinary multiplication, $\times$; Is $\mathbb{R}$ a group under multiplication?
   集合：$\mathbb{R}$（实数集）；二元运算：普通乘法 $\times$；实数集 $\mathbb{R}$ 关于乘法是否构成群？

Abstract Algebra Interview 2

抽象代数访谈 2

In addition to Definition 1, the following definitions were given in the second interview. The last two were new to the students.
第二次访谈中，除定义 1 外，还提供了以下定义，其中后两个定义对学生而言是全新的。

Definition 2 Suppose $K$ is a subgroup of a group $G$ and $a$ is an element of $G$. The set { a y : y ∈ K } \{ a y : y \in K \} {ay:y∈K} is called a left coset of $K$ in $G$. It is denoted by $aK$.
定义 2 设 $K$ 是群 $G$ 的子群（subgroup），$a\in G$。集合 { a y ∣ y ∈ K } \{ a y \mid y \in K \} {ay∣y∈K} 称为 $K$ 在 $G$ 中的一个左陪集（left coset），记为 $aK$。

Definition 3 Suppose $K$ is a subgroup of a group $G$. We define $G/K$ to be the set of all left cosets of $K$ in $G$. In other words, G / K = { a K : a ∈ G } G / K = \{ a K : a \in G \} G/K={aK:a∈G}.
定义 3 设 $K$ 是群 $G$ 的子群。定义 $G/K$ 为 $K$ 在 $G$ 中的所有左陪集构成的集合，即 G / K = { a K ∣ a ∈ G } G / K = \{ a K \mid a \in G \} G/K={aK∣a∈G}。

Definition 4 Suppose $K$ is a subgroup of a group $G$. For left cosets $bK$ and $cK$ of $K$ in $G$, we define $(bK)(cK)=bcK$.
定义 4 设 $K$ 是群 $G$ 的子群。对 $K$ 在 $G$ 中的任意两个左陪集 $bK$ 和 $cK$，定义 $(bK)(cK)=bcK$。

Each student was given the following task to complete based on the definitions. The symmetry group of the square is denoted $D_4$, and $F$ denotes a reflection across one of the diagonals.
基于上述定义，每位学生需完成以下任务：正方形的对称群记为 $D_4$，$F$ 表示沿某一对角线的反射变换（reflection）。

Consider the subgroup $⟨F⟩$ of the group $D_4$ under the operation of composition.
考虑在复合运算（composition）下，群 $D_4$ 的子群 $⟨F⟩$（由 $F$ 生成的子群）。

1. Find $D_4/⟨F⟩$.
   求 $D_4/⟨F⟩$（即子群 $⟨F⟩$ 在 $D_4$ 中的所有左陪集构成的集合）。

2. Is $D_4/⟨F⟩$ a group where $(b⟨F⟩)(c⟨F⟩)$ is defined by Definition 4?
   若按定义 4 定义运算 $(b⟨F⟩)(c⟨F⟩)$，则 $D_4/⟨F⟩$ 是否构成群？

ACKNOWLEDGMENT

致谢

The authors gratefully acknowledge support from the National Science Foundation and the Oregon Collaborative for Excellence in the Preparation of Teachers (DUE-9653250).
作者衷心感谢美国国家科学基金会（National Science Foundation）和俄勒冈教师培养卓越合作项目（Oregon Collaborative for Excellence in the Preparation of Teachers，项目编号 DUE-9653250）提供的支持。

REFERENCES

参考文献

1. The American Heritage Dictionary of the English Language, 4th ed., Houghton Mifflin, Boston, 2000.
   《美国传统英语词典》(第 4 版),霍顿･米夫林出版公司(Houghton Mifflin),波士顿,2000 年｡

2. M. Asiala, E. Dubinsky, D. Mathews, S. Morics, and A. Oktac, Student understanding of cosets, normality and quotient groups, J. Math. Behavior 16 (1997) 241-309.
   M. 阿西亚拉(Asiala)､E. 杜宾斯基(Dubinsky)､D. 马修斯(Mathews)､S. 莫里克斯(Morics)､A. 奥克塔克(Oktac),《学生对陪集､正规性和商群的理解》,《数学行为期刊》(J. Math. Behavior),第 16 卷(1997 年),第 241-309 页｡

3. A. Brown, D. DeVries, E. Dubinsky, and K. Thomas, Learning binary operations, groups, and subgroups, J. Math. Behavior 16 (1997) 187-289.
   A. 布朗(Brown)､D. 德弗里斯(DeVries)､E. 杜宾斯基(Dubinsky)､K. 托马斯(Thomas),《二元运算､群与子群的学习》,《数学行为期刊》(J. Math. Behavior),第 16 卷(1997 年),第 187-289 页｡

4. W. Burger and J. M. Shaughnessy, Characterizing the van Hiele levels of development in geometry, J. Research in Math. Education 16 (1986) 31-48.
   W. 伯格(Burger)､J. M. 肖内西(Shaughnessy),《几何范･希尔发展水平的特征描述》,《数学教育研究期刊》(J. Research in Math. Education),第 16 卷(1986 年),第 31-48 页｡

5. B. Edwards, Undergraduate mathematics majors’ understanding and use of formal definitions in real analysis, unpublished doctoral dissertation, Pennsylvania State University, 1997.
   B. 爱德华兹(Edwards),《本科数学专业学生对实分析中形式化定义的理解与使用》,未发表博士论文,宾夕法尼亚州立大学,1997 年｡

6. -, An undergraduate student’s understanding and use of mathematical definitions in real analysis, in Proceedings of the Nineteenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, vol. 1, ERIC Clearinghouse for Science, Mathematics and Environmental Education, Columbus, OH, 1997, pp. 17-22.
   同上,《一名本科生对实分析中数学定义的理解与使用》,收录于《国际数学教育心理学协会北美分会第十九届年会论文集》(第 1 卷),ERIC 科学､数学与环境教育资源中心,俄亥俄州哥伦布市,1997 年,第 17-22 页｡

7. G. R. Exner, An Accompaniment to Higher Mathematics, Springer-Verlag, New York, 1996.
   G. R. 埃克斯纳(Exner),《高等数学辅助教程》(An Accompaniment to Higher Mathematics),施普林格出版社(Springer-Verlag),纽约,1996 年｡

8. G. Harel and L. Sowder, Students’ proof schemes: Results from exploratory studies, in Issues in Mathematics Education Vol. 7: Research in Collegiate Mathematics Education. III, A. H. Schoenfeld et al., eds., American Mathematical Society, Providence, 1998, pp. 234-383.
   G. 哈雷尔(Harel)､L. 索德(Sowder),《学生的证明方案:探索性研究结果》,收录于《数学教育问题》第 7 卷:《大学数学教育研究(III)》,A. H. 舍恩菲尔德(Schoenfeld)等主编,美国数学学会(American Mathematical Society),普罗维登斯,1998 年,第 234-383 页｡

9. D. W. Henderson, Experiencing Geometry in Euclidean, Spherical and Hyperbolic Spaces, 2nd ed., Prentice Hall, Upper Saddle River, NJ, 2001.
   D. W. 亨德森(Henderson),《欧几里得､球面与双曲空间中的几何体验》(第 2 版),普伦蒂斯･霍尔出版社(Prentice Hall),新泽西州上萨德尔河,2001 年｡

10. S. I. Landau, Dictionaries: The Art and Craft of Lexicography, 2nd ed., Cambridge University Press, Cambridge, 2001.
    S. I. 兰道(Landau),《词典:词典编纂的艺术与技巧》(第 2 版),剑桥大学出版社(Cambridge University Press),剑桥,2001 年｡

11. R. C. Moore, Making the transition to formal proof, Educational Studies in Math. 27 (1994) 249-266.
    R. C. 穆尔(Moore),《向形式化证明的过渡》,《数学教育研究》(Educational Studies in Math.),第 27 卷(1994 年),第 249-266 页｡

12. L. Pereira-Mendoza, What is a quadrilateral?, Math. Teacher 86 (1993) 774-776.
    L. 佩雷拉 - 门多萨(Pereira-Mendoza),《什么是四边形?》,《数学教师》(Math. Teacher),第 86 卷(1993 年),第 774-776 页｡

13. Principles and Standards for School Mathematics, The National Council of Teachers of Mathematics, Reston, VA, 2000.
    《学校数学原则与标准》(Principles and Standards for School Mathematics),美国国家数学教师委员会(The National Council of Teachers of Mathematics),弗吉尼亚州雷斯顿,2000 年｡

14. F. J. Prevost, Geometry in the junior high school, Math. Teacher 79 (1985) 411-417.
    F. J. 普雷沃斯特(Prevost),《初中几何教学》,《数学教师》(Math. Teacher),第 79 卷(1985 年),第 411-417 页｡

15. R. Robinson, Definition, Oxford University Press, London, 1954; reprinted by D. R. Hillman & Sons, Frome, U.K., 1962.
    R. 罗宾逊(Robinson),《定义》(Definition),牛津大学出版社(Oxford University Press),伦敦,1954 年;英国弗罗姆市 D. R. 希尔曼父子出版社(D. R. Hillman & Sons)1962 年重印｡

16. A. Selden and J. Selden, Validations of proofs considered as texts: Can undergraduates tell whether an argument proves a theorem? J. Research in Math. Education 34 (2003) 4-36.
    A. 塞尔登(Selden)､J. 塞尔登(Selden),《作为文本的证明有效性检验:本科生能否判断一个论证是否证明了定理?》,《数学教育研究期刊》(J. Research in Math. Education),第 34 卷(2003 年),第 4-36 页｡

17. D. Solow, How To Read and Do Proofs: An Introduction to Mathematical Thought Processes, 3rd ed., John Wiley & Sons, New York, 2002.
    D. 索洛(Solow),《如何阅读与撰写证明:数学思维过程导论》(第 3 版),约翰･威利父子出版社(John Wiley & Sons),纽约,2002 年｡

18. I. Stewart, Nature’s Numbers: Discovering Order and Pattern in the Universe, Weidenfeld & Nicholson, London, 1995.
    I. 斯图尔特(Stewart),《自然的数字:探索宇宙中的秩序与模式》(Nature’s Numbers: Discovering Order and Pattern in the Universe),韦登菲尔德与尼科尔森出版社(Weidenfeld & Nicholson),伦敦,1995 年｡

19. D. Tall, The transition to advanced mathematical thinking: Functions, limits, infinity and proof, in NCTM Handbook of Research on Mathematics Teaching and Learning, D. A. Grouws, ed., Macmillan, New York, 1992, pp. 495-511.
    D. 托尔(Tall),《向高等数学思维的过渡:函数､极限､无穷与证明》,收录于《NCTM 数学教与学研究手册》,D. A. 格鲁斯(Grouws)主编,麦克米伦出版社(Macmillan),纽约,1992 年,第 495-511 页｡

20. D. J. Velleman, How To Prove It: A Structured Approach, Cambridge University Press, Cambridge, 1994.
    D. J. 维勒曼(Velleman),《如何证明:结构化方法》(How To Prove It: A Structured Approach),剑桥大学出版社(Cambridge University Press),剑桥,1994 年｡

21. S. Vinner, The Role of Definitions in the Teaching and Learning of Mathematics, in Advanced Mathematical Thinking, D. Tall, ed., Kluwer, Dordrecht, 1991, pp. 65-81.
    S. 文纳(Vinner),《定义在数学教与学中的作用》,收录于《高等数学思维》,D. 托尔(Tall)主编,克卢维尔出版社(Kluwer),多德雷赫特,1991 年,第 65-81 页｡

Author Biographies

作者简介

BARBARA S. EDWARDS received her Ph.D. in mathematics education from Pennsylvania State University in 1997 (thus beginning her third career). Her research interests are in advanced mathematical thinking and the teaching and learning of undergraduate mathematics. She is an associate professor in the Mathematics Department at Oregon State University.
芭芭拉・S・爱德华兹（BARBARA S. EDWARDS）于 1997 年从宾夕法尼亚州立大学获得数学教育博士学位（自此开启了她的第三份职业生涯）。她的研究方向为高等数学思维及本科数学教与学。她现任俄勒冈州立大学数学系副教授。

Oregon State University, Corvallis, OR 97331
俄勒冈州立大学，科瓦利斯，俄勒冈州，97331

edwards@math.orst.edu

MICHAEL B. WARD was an undergraduate at Utah State University and received a Ph.D. from the University of Utah in 1979. He worked at Bucknell University until 1997, when he moved to Western Oregon University, thereby fulfilling a twelve-year family dream of living in the offbeat state of Oregon. Besides trying to prove the occasional theorem in group theory, he enjoys reading, walking, and spending time with his wife Elizabeth and his children Hans, Liesl, and Maren.
迈克尔・B・沃德（MICHAEL B. WARD）本科毕业于犹他州立大学，1979 年从犹他大学获得博士学位。1997 年前，他任职于巴克内尔大学，之后转至西俄勒冈大学，实现了家庭长达 12 年的愿望 —— 定居于充满特色的俄勒冈州。除了偶尔研究群论中的定理证明外，他还喜欢阅读、散步，并与妻子伊丽莎白（Elizabeth）及子女汉斯（Hans）、莉斯尔（Liesl）、玛伦（Maren）共度时光。

Department of Mathematics, Western Oregon University, Monmouth, OR 97361
西俄勒冈大学数学系，蒙茅斯，俄勒冈州，97361

wardm@wou.edu

---

Do names given to math concepts have a role in common mistakes by students?

数学概念的命名是否会导致学生常见的错误？

Perhaps this question overlaps with similar ones, … but I want to focus on a particular possible cause of confusion. I notice that students are often confused by the concepts of “infinite” and “unbounded”. So, when asked if the set of invertible matrices is compact, they reply “no, because there are an infinite number of matrices with non-zero determinant, therefore the set is unbounded”. Actually this happens in Italian, where the corresponding words (“infinito” and “illimitato”) are almost synonyms in everyday language. Does this happen in English too, or other languages? I wonder: what if we chose another name for the two concepts? Would they make this mistake anyway? One way to check this would be to compare with what happens in other languages, where perhaps the words chosen do not create the confusion. Do you have other examples of this situation? Can you suggest different math concepts which in one language are named with synonyms, but not in another? Do you know if this problem has been studied anywhere?
这个问题可能与一些类似的问题有所重叠…… 但我想要关注一个特定的可能的混淆原因。我注意到学生们常常会混淆 “无限” 和 “无界” 这两个概念。所以，当被问及可逆矩阵的集合是否是紧致的时，他们会回答 “不，因为存在无穷多个行列式非零的矩阵，因此这个集合是无界的”。实际上这种情况在意大利语中也会出现，因为在日常语言中，“infinito”（无限）和 “illimitato”（无界）几乎是同义词。这种情况在英语中也会出现吗，或者在其他语言中呢？我在想：如果我们为这两个概念选择另一个名字，学生们还会犯这个错误吗？检验这一点的一个方法是与其他语言进行比较，也许在其他语言中，所选用的词汇不会造成这种混淆。你还有其他类似的情况吗？你能提出一些在一种语言中用同义词命名但在另一种语言中不是的不同的数学概念吗？你知道这个问题在任何地方被研究过吗？

edited Jun 18, 2010 at 11:26
– Diego Matessi 67%

Your actual question seems to be more specific and linguistically oriented than your title question. (I’m sure everyone would agree that the answer to the title question is a resounding yes.) Would you consider editing the title to better match the question?
你的实际问题似乎比标题问题更具体、更具语言学倾向。（我相信每个人都会同意标题问题的答案是响亮的 “是”。）你是否考虑修改标题以更好地匹配问题？

– Pete L. Clark
Commented Jun 18, 2010 at 12:00

Infinite and unbounded probably don’t have much of a distinction for nonmathematicians in English either, but they make sense once one gets used to them. Most of my fellow students (even those not intending to become mathematicians) find the terminology mostly logical, although Spiro’s answer may be an exception…nevertheless, people make mistakes with definitions without regard to other definitions anyway, and it’s part of learning the definition in the first place, so I think that for the most part students should just be encouraged to think longer.
对于非数学家来说，在英语中 “无限” 和 “无界” 的区别可能也不大，但一旦习惯了它们，它们就说得通了。我的大多数同学（即使是那些不打算成为数学家的人）也认为这些术语大多合乎逻辑，尽管斯皮罗的回答可能是个例外…… 不管怎样，人们在定义上犯错误时本来就不考虑其他定义，这也是学习定义本身的一部分，所以我认为在大多数情况下，学生们应该被鼓励多思考。

– user1437
Commented Jun 18, 2010 at 13:25

@Pete L. Clark. I don’t know how to change the question. The reference to languages is just a suggestion on how one could find out whether it is the names which cause the confusion. Simply because other languages may have chosen better names. The answers that are coming in are in theme. Thank you all…
@彼特・L・克拉克。我不知道如何更改问题。提到语言只是建议人们如何找出是否是名称导致了混淆。仅仅是因为其他语言可能选择了更好的名称。收到的答案都符合主题。感谢大家……

– Diego Matessi
Commented Jun 18, 2010 at 14:09

Suppose, in your language, the word for “multiplication” resembles a nasty word. Perhaps that would be distracting for students. In English, in some 18th century writing, we find a polynomial is called “sexual” if it has degree six. We don’t say that any more!
假设在你的语言中，“乘法” 一词类似于一个令人不快的词。也许这会分散学生的注意力。在英语中，在一些 18 世纪的著作中，我们发现如果一个多项式的次数为六，则称其为 “性” 的。我们现在不再这样说！

– Gerald Edgar
Commented Feb 27, 2012 at 19:08

I feel “adjoint” also falls under this category
我觉得 “伴随” 也属于这一类

Commented Sep 29, 2016 at 6:32
– Rune

Answers

“Open” and “closed”. Every reasonable human being on the planet, who has not studied topology, will assume that something can either be open or closed, but not both. This often causes students to make statements like “Set A is open, therefore it is not closed, thus …”
“开” 和 “闭”。这个星球上每一个合理的没有学过拓扑学的人，都会认为某物要么是开的，要么是闭的，但不能两者都是。这常常导致学生们说出这样的话：“集合 A 是开的，因此它不是闭的，因此……”

answered Jun 18, 2010 at 13:27
– Rune

Perhaps open sets should be called exposed sets, and closed sets should be called clothed sets (you can see the interior through a dotted line, but the solid line prevents you from looking inside). This would be consistent with some pictures in ${\mathbb{R}}^2$ and ${\mathbb{R}}^3$ students see early on. And then, later, you can talk about sets being clothed and exposed. If a student says that a set cannot be exposed and clothed, you just have to mention Lady Gaga.
也许应该把开集称为暴露集，把闭集称为遮盖集（你可以通过虚线看到内部，但实线会阻止你看到内部）。这与学生们早期看到的 ${\mathbb{R}}^2$ 和 ${\mathbb{R}}^3$ 中的一些图片是一致的。然后，稍后，你可以谈论集合是遮盖的还是暴露的。如果一个学生说一个集合不能既暴露又遮盖，你只需要提到 Lady Gaga。

– Marty
Commented Jun 18, 2010 at 15:18

At least concluding a set is not closed because it’s open makes sense for a proper, non-empty subset of a connected space. Worse is the reasoning “Since $A$ is not open, it must be closed.”
至少对于连通空间的非空真子集来说，因为一个集合是开的就得出它不是闭的这一结论是说得通的。更糟糕的是这样的推理：“因为 $A$ 不是开的，所以它一定是闭的。”

– PersonX
Commented Jun 18, 2010 at 16:03

Can’t resist quoting a comment from another thread: Munkres is fond of saying: “Sets are not doors!”. Also, there are, of course, spaces with clopen sets.
忍不住引用另一个讨论中的评论：Munkres 喜欢说：“集合不是门！” 当然，还有存在既开又闭的集合的空间。

– Victor Protsak
Commented Jun 19, 2010 at 2:22

It’s a bit clunky, perhaps, but I always thought ‘enclosed’ for closed and ‘edgeless’ for open captured the intuition from open/closed intervals without introducing problems that occur by the natural linguistic analogy to doors. ‘Enclosed’ because you can’t get out (with a sequence), ‘edgeless’ because, well, there are no edges.
这可能有点笨拙，但我一直认为 “封闭的” 用于闭集，“无边的” 用于开集，能够捕捉到开区间和闭区间的直觉，而不会引入因语言上自然类比到门而产生的问题。“封闭的” 是因为你无法（通过序列）出去，“无边的” 是因为，嗯，没有边界。

– Ketil Tveiten
Commented Jun 19, 2010 at 12:12

But it can be ajar!
但它可以是半开的！

– timur
Commented Jan 20, 2011 at 2:54

My favourite is this: some books use “completely reducible” for semi-simple and “irreducible” for simple. As a result, every irreducible module is completely reducible.
我最喜欢的是这个：一些书用 “完全可约” 来表示半单，“不可约” 来表示单。结果就是，每一个不可约模都是完全可约的。

answered Jun 18, 2010 at 13:10

– Spiro Karigiannis

“Semisimple” is not without its perils: for example, 1-dimensional abelian Lie algebra is simple, but it’s not semisimple! (There are good reasons for making this choice: I just want to point out that making sure that naive parsing works isn’t always the goal.)
“半单” 并非没有其危险之处：例如，一维阿贝尔李代数是单的，但它不是半单的！（做出这种选择是有充分理由的：我只是想指出，确保天真地解析总是有效的并非总是目标。）

– Victor Protsak
Commented Jun 19, 2010 at 2:20

If you count “or” as a mathematical concept, the fact that it is fundamentally inclusive in mathematics but often exclusive in most other uses of English can lead students to mistakes.
如果你把 “或” 算作一个数学概念，那么它在数学中本质上是包容的，但在英语的大多数其他用法中通常是排他的，这会导致学生犯错误。

answered Jun 18, 2010 at 11:52
– Q.Q.J.

This reminds me about the French version of “or” and a related puzzle which I learned from Don. He can’t find an explanation of why one of the extended letters on French keyboards does not come as the whole word in which it is only used. And this is the word very often used in maths! (As this is a puzzle I am not supposed to provide the answer, but I know that it is not very obvious: ù.)
这让我想起了法语版本的 “或” 和一个相关的谜题，我是从唐那里学到的。他找不到一个解释，为什么法语键盘上的一个扩展字母并不以它唯一使用的那个完整单词的形式出现。而这个单词在数学中非常常用！（因为这是一个谜题，我不应该提供答案，但我知道它并不显而易见：ù。）

– Wadim Zudilin
Commented Jun 18, 2010 at 12:13

Où in fact translates to where, which is nevertheless common in mathematics. (Ou, without the accent, is French for or.)
“Où” 实际上翻译为 “哪里”，尽管在数学中也很常见。（没有重音符号的 “Ou” 是法语中的 “或”。）

– Niel de Beaudrap
Commented Jun 18, 2010 at 13:04

“Or” is not the same as “exclusive or” in English if there are three or more disjuncts. “A or B or C” in English commonly means “exactly one of A, B, C” whereas “A xor B xor C” is true if and only if an odd number of disjuncts holds.
如果存在三个或更多不相交的项，“或” 在英语中与 “异或” 不同。“A 或 B 或 C” 在英语中通常意味着 “A、B、C 中恰好有一个”，而 “A xor B xor C” 只有在奇数个不相交项成立时才为真。

– Timothy Chow
Commented Jun 18, 2010 at 14:04

And it gets even more xorsting as the number of disjuncts increases!
而且随着不相交项的数量增加，情况变得更加复杂！

– Q.Q.J.
Commented Jun 18, 2010 at 16:00

You just need a little xorcise…
你只需要一点 “异或锻炼”……

– Victor Protsak
Commented Jun 19, 2010 at 9:08

I’m surprised nobody has mentioned “one-to-one function” for injection and “one-to-one correspondence” for bijection.
我很惊讶没有人提到用 “一一函数” 表示单射，用 “一一对应” 表示双射。

answered Feb 28, 2012 at 19:26
– JeffE

I hadn’t realized that in teaching (maybe because I teach subjects where those terms rarely arise), but now that you mention it that did confuse me when I was a student…
我没有意识到在教学中（也许是因为我教的科目中这些术语很少出现），但现在你提到这一点，我在当学生时确实被这些术语搞糊涂了……

– Michael Lugo
Commented Feb 29, 2012 at 0:13

I didn’t even realize this was a thing! For me, the word “correspondence” just means “binary relation between two sets.”
我甚至没有意识到这是一个问题！对我来说，“对应” 这个词只是意味着 “两个集合之间的二元关系”。

– goblin GONE
Commented Mar 5, 2016 at 8:02

It’s not just students who get confused by terminology. I was recently puzzled for quite a while until I realized that finite von Neumann algebras can be infinite-dimensional.
不仅仅是学生会被术语搞糊涂。我最近也困惑了相当一段时间，直到我意识到有限冯・诺伊曼代数可以是无限维的。

edited Feb 28, 2012 at 0:13
– Peter Shor 50%

And separable von Neumann algebras need not be separable.
而且可分的冯・诺伊曼代数不一定是可分的。

– Richard Borcherds
Commented Jul 19, 2010 at 4:08

And a hyperfinite von Neumann algebra can be properly infinite.
而且超有限的冯・诺伊曼代数可以是真正的无限的。

– M Mueger
Commented Nov 16, 2015 at 23:27

My favourite example is “complex analysis” (as well as “complex” and “imaginary” numbers). Students, mostly in advance, feel it too complex. There should be probably a better name but it’s too late to change…
我最喜欢的例子是 “复分析”（以及 “复数” 和 “虚数”）。学生们大多会提前觉得它太复杂了。也许应该有一个更好的名字，但现在改已经太晚了……

answered Jun 18, 2010 at 11:26
– Wadim Zudilin

I agree that “complex” has unfortunate overtones, but it does allow one to say things like “Let’s complexify this to simplify it.”. On second thoughts, perhaps that’s a good reason to find a new term for it!
我同意 “复” 这个词有不幸的含义，但它确实允许人们说 “让我们复化这个以简化它” 之类的话。再想想，也许这正是为它找一个新术语的好理由！

– Andrew Stacey
Commented Jun 18, 2010 at 11:46

And how did we ever allow ourselves to say “complex simple Lie algebras”!?
我们是怎么让自己说出 “复单李代数” 这种话的？！

– John Stillwell
Commented Jun 18, 2010 at 12:03

Niel: Gauss complained about the real/imaginary terminology. A quote: “That this subject [imaginary numbers] has hitherto been surrounded by mysterious obscurity, is to be attributed largely to an ill adapted notation. If, for example, +1, -1, and the square root of -1 had been called direct, inverse and lateral units, instead of positive, negative and imaginary (or even impossible), such an obscurity would have been out of the question.”
尼埃尔：高斯抱怨过实数 / 虚数的术语。有一段引文：“到目前为止，这个主题 [虚数] 一直被神秘的晦暗所包围，这在很大程度上要归因于不合适的符号。例如，如果 + 1、-1 和 - 1 的平方根被称为正向单位、反向单位和侧向单位，而不是正数、负数和虚数（甚至是不可能的数），那么这种晦暗就不存在了。”

– KConrad
Commented Jun 18, 2010 at 19:49

Wadim, I am sure you’ve heard about the professor who wrote a very complicated equation on the board and with his characteristic modesty, called it an ordinary differential equation (cited by V.I. Arnold).
瓦迪姆，我相信你听说过那位教授在黑板上写了一个非常复杂的方程，并且以他特有的谦逊，称之为常微分方程（V.I. 阿诺德引用）。

– Victor Protsak
Commented Jun 19, 2010 at 2:16

Excellent point, except for the “too late to change” part. If it helps that much, we should probably just do it. There’s only a finite amount of historical work to rephrase, but there’s a potentially unbounded number of future students to benefit.
非常好的观点，除了 “太晚改变” 这一点。如果这真的有很大帮助，我们或许应该去做。需要重新措辞的历史工作是有限的，但未来可能会有无限多的学生从中受益。

– Noah
Commented Jun 19, 2010 at 22:47

The article “Surprises from mathematics education research: student (mis) use of mathematical definitions” by Edwards and Ward addresses some of your concerns in the context of U.S. undergraduates.
爱德华兹和沃德的文章《数学教育研究中的意外：学生对数学定义的（误）用]》在研究美国本科生的背景下，回应了你的一些担忧。

From the introduction:
从引言中：

…[T] asks involving the definitions of “limit” and “continuity,” for example, were problematic for some of the students. Ward’s intuitive reaction was that those words were “loaded” with connotations from their nonmathematical use and from their less than completely rigorous use in elementary calculus. He said, “I’ll bet students have less difficulty or, at least, different difficulties with definitions in abstract algebra. The words there, like ‘group’ and ‘coset,’ are not so loaded.”
例如，涉及 “极限” 和 “连续性” 定义的任务对一些学生来说是有问题的。沃德的直觉反应是，这些词汇在非数学用法中以及在初等微积分中不完全严谨的使用中带有 “沉重的” 联想。他说：“我敢打赌，学生们在抽象代数的定义上遇到的困难会少一些，或者至少是不同的困难。那里的词汇，比如‘群’和‘陪集’，并没有那么沉重的联想。”
…
He was surprised to see his algebra students having difficulties very similar to those of Edwards’s analysis students. (So he lost his bet.) In particular, he was surprised to see difficulties arising from the students’ understanding of the very nature of mathematical definitions, not just from the content of the definitions.
他惊讶地发现他的代数学生的困难与爱德华兹的分析学生的困难非常相似。（所以他输了。）特别是，他惊讶地发现困难源于学生对数学定义的本质的理解，而不仅仅是定义的内容。

answered Jul 18, 2010 at 20:18
– Jonas Meyer

Here’s a link to the pdf from Ward’s website, in case you don’t have JSTOR: wou.edu/~wardm/FromMonthlyMay2004.pdf
这是沃德网站上的 pdf 链接，以防你没有 JSTOR：wou.edu/~wardm/FromMonthlyMay2004.pdf

– Jonas Meyer
Commented Jul 19, 2010 at 0:47

That is an interesting article, but its relevance to the present question seems to be confined to the distinction the authors draw between word definitions that are “extracted” (from use) and “stipulated” (by arbitrary rules). If anything, their “surprising” conclusion, based on limited data, is that even in the absence of an obvious connotation, students presented with a new, entirely abstract definition will try to relate it to mental images of things they have seen and used before rather than proceed literally from the definition. Duh! (They passed the Turing test.)
这是一篇有趣的文章，但它与当前问题的相关性似乎仅限于作者对 “提取的”（从使用中）和 “规定的”（由任意规则）词汇定义之间的区分。如果有什么的话，他们基于有限数据得出的 “惊人” 结论是，即使在没有明显联想的情况下，面对一个全新的、完全抽象的定义的学生也会尝试将其与他们之前看到和使用过的东西的思维图像联系起来，而不是从定义本身出发。哎呀！（他们通过了图灵测试。）

– Victor Protsak
Commented Jul 19, 2010 at 6:39

There are many questions in the present question, but among them is to what extent do the words’ ordinary meanings affect students’ misunderstandings. The authors of this article claim that the effect didn’t show up in their study; “coset” has no ordinary meaning as opposed to “limit”, and yet similar problems were observed among undergraduates regarding misuse of both. At least, that is what I took out of it, and why I thought it was relevant.
当前问题中有许多问题，但其中之一是这些词汇的普通含义在多大程度上影响学生的误解。这篇文章的作者声称这种影响在他们的研究中没有显现出来；“陪集” 没有普通含义，与 “极限” 不同，然而在本科生中观察到的对两者的误用却出现了类似的问题。至少，这是我从中得出的结论，也是我认为它相关的原因。

– Jonas Meyer
Commented Jul 19, 2010 at 17:30

The idea that ‘group’ (or ‘ring’ or ‘field’ or’sheaf’) doesn’t have everyday meaning is a little strange….
“群”（或 “环” 或 “域” 或 “层”）没有日常含义的想法有点奇怪……

– LSpice
Commented Feb 17, 2016 at 21:14

I agree with L. Spice, looking back at this; why would “group” be less loaded than “continuity”?
我同意 L・斯派斯的观点，回顾一下这个问题；为什么 “群” 比 “连续性” 更不沉重呢？

– Jonas Meyer
Commented Mar 1, 2017 at 1:38

Not only is the word “complex” a problem, the word “simple” is too. I mean, how “simple” are the sporadic simple groups? I have to tell my students that “simple” does not mean “not complicated”, but rather “cannot be simplified further.”
“复” 这个词是个问题，“单” 这个词也是。我的意思是，那些散在的单群有多 “单” 呢？我不得不告诉我的学生，“单” 并不意味着 “不复杂”，而是 “不能再简化了”。

answered Jun 18, 2010 at 12:11
– John Stillwell

Is a simple polyhedron one that (a) has genus zero, (b) is triangulated, i.e., simplicial, or © has all vertices of degree 3? One can find all three in the literature.
一个单多面体是（a）亏格为零，（b）被三角化的，即单体的，还是（c）所有顶点的度数为 3 的呢？在文献中可以找到这三种说法。

– Joseph O’Rourke
Commented Jun 18, 2010 at 13:13

Worse still, what could a “complex simple Lie algebra” possibly be?
更糟糕的是，“复单李代数” 到底可能是什么？

– Allen Knutson
Commented Jun 18, 2010 at 14:12

Or simplicial complex?
或者单体复形呢？

– Victor Protsak
Commented Jun 19, 2010 at 2:13

Or my favorite from Lang’s “Algebra”: “a ring $R$ is said to be simple if it is semisimple and … .”
或者来自朗的《代数》中我最喜欢的说法：“如果环 $R$ 是半单的……，就说它是单的。”

– Chris Leary
Commented Feb 29, 2012 at 3:47

What kind of errors follow from the fact that “simple” does not mean “not complicated” and complex does not mean “complicated”? I can’t imagine that this is really a problem.
“单” 并不意味着 “不复杂”，“复” 也不意味着 “复杂”，这会引发什么样的错误呢？我真的无法想象这会是一个真正的问题。

– miracle173
Commented Aug 28, 2016 at 9:18

I don’t know of any research on this question specific to learning about mathematics. But the question opens up a big can of academic worms, outside of mathematics.
我不知道有没有任何专门针对学习数学的这个问题的研究。但这个问题在数学之外引发了一个巨大的学术问题罐子。

In linguistics, the Whorf hypothesis (sometimes called the Sapir-Whorf hypothesis) can be summarized as the notion that different peoples have different languages (syntax, lexicon, etc.), and these differences influence how they think about things. For example, different languages have different tenses available for use – does this affect how speakers perceive time?
在语言学中，沃尔夫假说（有时也称为萨丕尔 - 沃尔夫假说）可以概括为不同民族有不同的语言（语法、词汇等），这些差异会影响他们对事物的看法。例如，不同语言有不同的时态可供使用 —— 这会影响说话者对时间的感知吗？

So, I’d say to start by looking up the Whorf hypothesis – maybe it’s been considered by some applied linguists studying education.
所以，我会说先去查找沃尔夫假说 —— 也许一些研究教育的应用语言学家已经考虑过这个问题。

The other linguistic can of worms is the use of metaphor in mathematical language. Some words we use are directly visual, like “smooth” and “compact”, some are strange (to me) analogies like “sheaf” and “flabby”, and others are part of larger metaphorical systems like “consider a variety over a finite field” (the use of the positional word “over”, to express dependence like a building resting on its foundation).
另一个语言学上的问题罐子是数学语言中隐喻的使用。我们使用的一些词汇是直接可视的，比如 “光滑” 和 “紧致”，一些是奇怪的（对我来说）类比，比如 “层” 和 “松软”，还有一些是更大隐喻系统的组成部分，比如 “考虑一个在有限域 上 的簇”（使用位置词 “上” 来表达依赖关系，就像建筑依赖于其基础一样）。

If you want to read up on these aspects of mathematical language, I’d recommend books by the Berkeley linguist Lakoff – the classic “Metaphors we live by*", and the application to mathematics in "Where mathematics comes from*”. Not that I agree with everything in the latter book, but it’s an interesting read. I don’t think you can address your question seriously without reviewing the linguistics literature.
如果你想了解数学语言的这些方面，我会推荐伯克利语言学家拉科夫的书 —— 经典的《我们赖以生存的隐喻》以及应用于数学的《数学从哪里来》。我不是同意后一本书中的所有内容，但它是一本有趣的书。我认为不回顾语言学文献，你就无法严肃地对待你的问题。

answered Jun 18, 2010 at 15:46
– Marty

I do not think that the Whorf hypothesis is taken very seriously these days.
我认为沃尔夫假说在这些天里并没有被非常认真地对待。

– Chris Godsil
Commented Jun 18, 2010 at 22:22

I don’t think it’s taken seriously by those who follow Steven Pinker’s criticisms – certainly it’s been taken down on a number of occasions. But I think it still rears its head in some contexts. The question definitely suggests Whorf to me…
我认为那些跟随史蒂文・平克批评的人并不认真对待它 —— 它肯定在许多场合被驳倒了。但我认为它在某些语境中仍然会冒出来。这个问题肯定让我想到了沃尔夫……

– Marty
Commented Jun 18, 2010 at 23:26

I agree with Marty, this Whorf hypothesis seems related. Also, it seems like one of the take-away messages I got from reading 1984, though I never knew it had a name. Thanks for writing this answer.
我同意马蒂的观点，沃尔夫假说似乎与这个问题有关。此外，它似乎也是我从读《1984》中得到的一个启示，尽管我以前不知道它有一个名字。感谢你写下这个回答。

– David White
Commented Feb 27, 2012 at 23:02

Actually these days it seems linguists (patterning after Noam Chomsky) think that “language affects cognition in /no/way”. So yes, a can of worms.
实际上，这些天来，语言学家（模仿诺姆・乔姆斯基）似乎认为 “语言 / 不 / 影响认知”。所以是的，这是一个问题罐子。

– Elizabeth S. Q. Goodman
Commented Feb 29, 2012 at 0:06

I don’t think this question has anything to do with what Whorf was suggesting. (And for that matter, I’m under the impression that what people refer to as the “Whorf hypothesis” is arguably rather stronger than Whorf himself would have argued for.) In any case, what’s at issue here is simple confusion of terminology. That happens in any language, in any field, and has nothing to do with the idea (quite likely wrong, or at least vastly overstated) that the inherent structure of a language has some determining effect on how its speakers view the world at large.
我认为这个问题与沃尔夫所暗示的内容没有任何关系。（顺便说一句，我的印象是，人们所说的 “沃尔夫假说” 可能比沃尔夫自己会论证的要强得多。）无论如何，这里的问题是简单的术语混淆。这种现象在任何语言、任何领域都会发生，与语言的固有结构对说话者如何看待整个世界有某种决定性影响的想法（很可能这是错误的，或者至少被大大夸大了）没有任何关系。

– Carl Offner
Commented Feb 29, 2012 at 2:02

This is very elementary, but I find it surprisingly common: many students talk about “infinite” numbers. You know, like
这非常基础，但我发现它出奇地常见：许多学生谈论 “无限的” 数字。你知道，比如

$$0.3333333\dots$$

answered Jun 19, 2010 at 2:17
– Victor Protsak

The problem here is not terminology, but that while such elementary concepts as this are taught, teachers stay as far away as possible from talking about infinity. There is no opportunity to discuss the difference between an infinitely long representation of a number, and a number which is’semantically’ infinite. Not that I advocate teaching infinite cardinals in grade-school, but if we did (or taught some other notion of infinity with some amount of seriousness), an immediate remedy would be to point out that $0.333333\dots$ is bounded between 0.3 and 0.4.
这里的问题不是术语，而是尽管像这样的基础概念被教授，但教师尽可能远离谈论无穷大。没有机会讨论一个数的无限长表示和 “语义上” 的无限数之间的区别。我不是主张在小学教授无限基数，但如果这样的话（或者以某种严肃的方式教授其他无限的概念），一个立即的补救办法就是指出 $0.333333\dots$ 被限制在 0.3 和 0.4 之间。

– Niel de Beaudrap
Commented Jun 19, 2010 at 9:35

Right. I suspect that teachers themselves are far from comfortable with infinity, and not just grade school teachers, either.
没错。我怀疑教师自己对无穷大也远非感到自在，不仅仅是小学教师。

– Victor Protsak
Commented Jun 19, 2010 at 10:29

I am far from comfortable with infinity as well… Fortunately understanding infinity is not a necessary condition to work in mathematics.
我对无穷大也远非感到自在…… 幸运的是，理解无穷大并不是从事数学工作的必要条件。

– darij grinberg
Commented Jul 18, 2010 at 21:11

I think this is a symptom of the teaching of most students wherein Calculus is the pinnacle of their education in mathematics. If someone takes a calculus class, doesn’t get an A on the sequences and series chapter and never thinks about sequences and series again, what can we expect them to pass on to others besides “funny things happen at infinity”?
我认为这是大多数学生数学教育的顶点是微积分课程的一个症状。如果有人上了一门微积分课，在序列和级数那一章没有拿到 A，之后再也不考虑序列和级数，我们还能期待他们向别人传递除了 “在无穷远处会发生有趣的事情” 之外的什么呢？

– stankewicz
Commented Jan 20, 2011 at 14:59

Oh, and “convex”. As far as convex sets go, the mathematical usage accords well with everyday language. Not so with convex (and concave) functions. Educationists (?) have tried to remedy this by using terms “concave up” and “concave down” in calculus textbooks, a usage that I detest. (I have a hard time remembering which is which of those two.)
哦，还有 “凸”。就凸 集 而言，数学用法与日常语言很相符。但凸（和凹）函数 并非如此。教育家（？）试图通过在微积分教科书中使用 “向上凹” 和 “向下凹” 这些术语来纠正这一点，但我很讨厌这种用法。（我很难记住这两个中哪个是哪个。）

Edited based on comments: It seems that in Russian, “convex” can refer a surface curved outward, where in English usually “convex” refers to a solid whose surface curves outward. Perhaps that’s why in complex geometry, one might consider a “convex domain” or its boundary, a “convex hypersurface”.
根据评论进行了编辑：似乎在俄语中，“凸” 可以指一个向外弯曲的表面，而在英语中，“凸” 通常指一个其表面向外弯曲的实体。也许这就是为什么在复几何中，人们可能会考虑一个 “凸域” 或其边界，一个 “凸超曲面”。

edited Feb 29, 2012 at 0:21
– Harald Hanche-Olsen 75%

Qiaochu, this is a classic situation where a picture is worth a thousand words. When I teach it, positive derivative $⟺\cup$ and negative derivative $⟺\cap$. Any language-based metaphor, no matter how clever, is bound to fail.
齐奥楚，这是一个经典的 “一图胜千言” 的情况。当我教这个时，正导数 $⟺\cup$，负导数 $⟺\cap$。任何基于语言的隐喻，无论多么巧妙，都注定会失败。

– Victor Protsak
Commented Jun 19, 2010 at 4:07

Ah, right. It’s concave up/down, not convex up/down. I’ll edit the answer accordingly. Now if we insist on language-based metaphors, wouldn’t “smiling” and “frowning” work better? (At least in 1 dimension.)
哦，对。是向上凹 / 向下凹，而不是向上凸 / 向下凸。我会相应地编辑答案。现在如果我们坚持使用基于语言的隐喻，“微笑” 和 “皱眉” 会不会更好呢？（至少在一维中。）

– Harald Hanche-Olsen
Commented Jun 19, 2010 at 14:05

Curiously, it is convex up/down in Russian. And which is which is clear, due to the ordinary (non-mathematical) meaning of the word.
有趣的是，在俄语中，它是向上凸 / 向下凸。而且由于这个词的普通（非数学）含义，哪一个是什么是清楚的。

– Sergei Ivanov
Commented Jun 19, 2010 at 18:59

No, “convex up” is concave (has negative second derivative). The word “convex” (adjective) in Russian means “bent outwards”, and “convexity” (noun) typically means a fragment of a surface resulting from such bending. For example, a low quality table surface may have “convexities” (small hill-shaped defects), and they are clearly convex up (i.e., a layer of the surface is bent up from its normal place).
不，“向上凸” 是凹的（二阶导数为负）。在俄语中，“凸”（形容词）意味着 “向外弯曲”，而 “凸性”（名词）通常意味着由于这种弯曲而形成的表面的一部分。例如，一张质量低下的桌子表面可能有 “凸起”（小山形缺陷），它们显然是向上凸的（即，表面的一层从其正常位置向上弯曲）。

– Sergei Ivanov
Commented Jun 19, 2010 at 20:50

“Smiling” and “frowning”, suggested by Harald a couple of comments above, suggest a great mnemonic: a function is happy if its second derivative is positive, and sad if it is negative.
哈拉尔德在上面的几条评论中提到的 “微笑” 和 “皱眉” 提供了一个很好的记忆方法：如果一个函数的二阶导数是正的，那么这个函数是快乐的；如果它是负的，那么这个函数是悲伤的。

– Federico Poloni
Commented Feb 27, 2012 at 18:53

I nominate “trivial”. It can be rather confusing that something can be trivial, but not trivially so.
我提名 “平凡”。有些东西可以是平凡的，但并不是平凡地如此，这可能会让人感到困惑。

answered Jun 18, 2010 at 12:48
– Harald Hanche-Olsen

“Trivial” as an adjective to a result is indeed subjective. But “trivial” as math concept is not and is what you expect: trivial group, trivial subgroup, etc.
“平凡” 作为形容词用于一个结果时确实是主观的。但作为数学概念的 “平凡” 并非如此，它就是你所期望的：平凡群、平凡子群等。

– lhf
Commented Jun 18, 2010 at 13:12

@LHF: First of all, in your examples of trivial being used as a math concept, it is also being used as an adjective (and indeed, this is always the case). Grammar aside, I think I disagree with your premise: the adjective “trivial” applied mathematically is context dependent and open to interpretation. For instance is a “trivial torsor” a torsor under a trivial group? what does it mean to say that a group or a space has “trivial cohomology”? Also we had a MO question about Bombieri’s intended meaning of “trivial solution” to a certain Diophantine equation.
@lhf：首先，在你将 “平凡” 用作数学概念的例子中，它也被用作形容词（事实上，这总是如此）。抛开语法不谈，我认为我不同意你的前提：在数学中应用的形容词 “平凡” 是依赖于上下文的，并且有多种解释。例如，“平凡扭子” 是一个平凡群下的扭子吗？说一个群或一个空间有 “平凡上同调” 是什么意思？此外，我们还曾有一个 MO 问题，关于邦别里对某个丢番图方程的 “平凡解” 的意图。

– Pete L. Clark
Commented Jun 18, 2010 at 17:00

…and is the ‘trivial map’ a constant map, or the identity?
……“平凡映射” 是一个常值映射，还是恒等映射？

– Ketil Tveiten
Commented Feb 28, 2012 at 8:30

Sequence vs series? Particularly if the two notions are introduced one right after the other in a calculus course, students are doomed to mix them up.
序列与级数？尤其是如果在微积分课程中一个紧接着另一个引入这两个概念，学生们注定会将它们混淆。

answered Jun 28, 2010 at 7:38
– Alfonso Gracia-Saz

But kids are doomed to mix left and right (which are in most cases introduced to them more or less consecutively) and at that point the two words probably do not mean anything to them. Maybe the problem is that when one is introduced to too many things (i.e. two) essentially at once confusion is to be expected?
但孩子们注定会混淆左和右（在大多数情况下，这两个概念是几乎连续地向他们介绍的），在那个时候，这两个词可能对他们来说没有任何意义。也许问题是当一个人一次性被介绍太多东西（即两个）时，出现混淆是可以预期的？

– Mariano Suárez-Álvarez
Commented Jul 19,2010 at 2:30

It’s a difficult distinction if it isn’t stressed: a sequence is a mathematical object. A series is a type of expression. Equality and identity coincide in the former, not in the latter.
如果不对这一点加以强调，这是一个很难区分的概念：序列是一个数学对象。级数是一种表达式。在前者中，相等和恒等是一致的，而在后者中则不是。

– AndrewLMarshall
Commented Dec 21, 2010 at 5:40

In Italian, the words bound and limit sound the same, “limite”. This often causes confusion, like in the limit points and the boundary points of a set or a bounded function and its limit.
在意大利语中，“bound”（有界）和 “limit”（极限）发音相同，都是 “limite”。这常常会导致混淆，比如集合的 极限点 和 边界点，或者 有界函数 及其 极限。

answered Feb 27, 2012 at 17:53
– alberto.bosia

An example is French module monogène for what is “cyclic module” in English. I can’t prove that the possibility that a module monogène for a given ring may not be a groupe cyclique would be a stumbling block for a student; but it shows the phenomenon (avoid overloading). (I learned this when Serre pulled up an anglophone lecturer speaking in French on one occasion.)
一个例子是法语中的 module monogène，在英语中是 “循环模”。我无法证明对于一个给定的环，module monogène 可能不是 groupe cyclique（循环群）这一可能性是否会成为学生的绊脚石；但它展示了这种现象（避免过载）。（我是从塞尔在一次场合中纠正一个用法语演讲的英语演讲者时学到的。）

answered Jun 18, 2010 at 11:34
– Charles Matthews

In French, a “monic polynomial” is a “polynôme unitaire”, and a “unit vector” is a “vecteur unitaire”. What happens to the students when they consider a dot product on a space of polynoms?
在法语中，“首一多项式” 是 “polynôme unitaire”，“单位向量” 是 “vecteur unitaire”。当学生们在一个多项式空间上考虑一个点积时，会发生什么呢？

answered Feb 28, 2012 at 20:59
– Julien Puydt

Similar situation in German (with ‘normiert’ instead of ‘unitaire’).
德语中也有类似的情况（用 “normiert” 代替 “unitaire”）。

– user9072
Commented Feb 29, 2012 at 0:52

In French, a “unitary endomorphism” is an “endomorphisme orthogonal”… and an “orthogonal projection” is a “projection orthogonale” (the ‘e’ is for female, it’s pronounced the same). You can hardly imagine how bad I feel when I have to tell my students that orthogonal projections aren’t unitary…
在法语中，“酉内自同态” 是 “endomorphisme orthogonal”…… 而 “正交投影” 是 “projection orthogonale”（“e” 是女性化的，发音相同）。你几乎无法想象当我不得不告诉我的学生正交投影不是酉的时，我有多难受……

answered Feb 28, 2012 at 20:56
– Julien Puydt

French has thousands of homonymic pairs of words: most French people seem to understand pretty well the difference between aimait, aimais, aimé, aimée, aimés, aimées, say. Why would university students have any trouble dealing with a few words that have two meanings?!
法语中有成千上万的同音词对：大多数法国人似乎很清楚像 aimait, aimais, aimé, aimée, aimés, aimées 这样的词的区别。为什么大学生会难以处理一些有两个含义的词呢？！

– Mariano Suárez-Álvarez
Commented Feb 28, 2012 at 23:34

Oh, another one where the same happens in German.
哦，德语中也有类似的情况。

– user9072
Commented Feb 29, 2012 at 0:54

@Mariano S-A: the words you cite are not all pronounced the same for one, and second, they’re just variants of the same word depending on grammar, so there’s definitely no trouble with them.
@马里亚诺 S-A：首先，你提到的这些词并不是都发音相同，其次，它们只是同一个词的不同语法变体，所以肯定不会对它们产生困惑。

– Julien Puydt
Commented Feb 29, 2012 at 9:55

For matrices, there is also the positive entry /positive semi-definite problem.
对于矩阵，还有正条目 / 半正定的问题。

– reuns
Commented Aug 28, 2016 at 17:02

I nominate the word “kernel” as the most abused term in mathematics. The null space of a linear operator, a symmetric positive definite function on a set, a smooth probability density peaked – am I missing any? I know these are all vaguely related, but the polysemy definitely causes much confusion for students.
我提名 “核” 这个词是数学中被滥用得最厉害的术语。线性算子的零空间，集合上的对称正定函数，平滑的概率密度峰值 —— 我漏掉了什么吗？我知道这些都有一些模糊的关联，但这种多义性确实让学生们感到非常困惑。

answered Aug 28, 2016 at 8:40
– Aryeh Kontorovich

---

Where Did Math Come From?

数学源自何处？

Did you know April is Math and Statistics Awareness Month? As we celebrate the significance of mathematics in our lives, it’s worth exploring how this universal language of numbers came to be. In this article, we’ll journey through history to uncover the birth of mathematics. From ancient civilizations devising early counting methods to the modern algorithms shaping our digital age.
你知道 4 月是数学与统计宣传月吗？在我们庆祝数学对生活的重要意义之际，不妨探究这门通用的数字语言是如何诞生的。本文将穿越历史，探寻数学的起源——从古代文明发明早期计数方法，到现代算法塑造数字时代。

Old Babylonian Area Calculation, Photo Source: Mathematical Association of America
古巴比伦面积计算

The Birth of Numbers:

数字的诞生：

In the earliest days of human civilization, counting was a necessity for survival. Primitive societies developed rudimentary methods of tallying, often using sticks, stones, or other objects to keep track of quantities.
在人类文明的最初阶段，计数是生存的必需。原始社会发明了基础的计数方式，常常用树枝、石头或其他物品来记录数量。

As societies evolved, so did their counting methods. Ancient Mesopotamians…, for example, devised one of the earliest numerical systems based on the concept of place value, using symbols to represent different quantities. Similarly, ancient Egyptians utilized hieroglyphics for numerical notation…, employing a system that played a role in various aspects of their society, including administrative tasks, trade, and record-keeping.
随着社会的发展，计数方法也在不断演变。例如，古代美索不达米亚人设计了最早的基于位值概念的数字系统，使用符号来表示不同的数量。同样，古埃及人也利用象形文字进行数字记录，这种系统在他们的社会中发挥了重要作用，包括行政管理、贸易和记录保存等多个方面。

The development of numerical notations paved the way for arithmetic operations, allowing humans to perform calculations with greater efficiency. From basic addition and subtraction to more complex multiplication and division, arithmetic became a cornerstone of early mathematical thinking.
数字符号系统的发展为算术运算奠定了基础，让人类能更高效地进行计算。从基础的加减法到复杂的乘除法，算术成为早期数学思维的核心基石。

Archimedes, Photo Source: History Extra
阿基米德

Ancient Mathematics:

古代数学：

Ancient civilizations, including Mesopotamians, Egyptians, Greeks, and Indians, made significant contributions to the development of mathematics. The ancient Mesopotamians, particularly the Sumerians and Babylonias, explored arithmetic, geometry, and algebra, with notable advancements in algebraic and quadratic equations.
美索不达米亚、埃及、希腊和印度等古代文明，为数学发展作出了重大贡献。古代美索不达米亚人（尤其是苏美尔人和巴比伦人）探索了算术、几何和代数，在代数方程和二次方程领域取得了显著进展。

Meanwhile, ancient Egyptians developed practical mathematics for taxation, trade, and construction, utilizing a $\text{base-}10$ numerical system and methods of multiplication, division, and fractions. Greek mathematicians such as Euclid, Pythagoras, and Archimedes pioneered geometry and mathematical proofs, establishing the foundations of formal mathematical reasoning with works like Euclid’s “Elements.”…
与此同时，古埃及人发展了实用数学，应用于税收、贸易和建筑领域，采用十进制数字系统以及乘除运算和分数计算方法。欧几里得、毕达哥拉斯和阿基米德等希腊数学家开创了几何学和数学证明的先河，通过《欧几里得几何原本》等著作，奠定了形式化数学推理的基础。

In India, mathematicians like Ayabhata and Brahmagupta made strides in arithmetic, algebra, and trigonometry, introducing concepts like zero and positional notation that revolutionized mathematical thinking worldwide. Together, these ancient mathematical traditions laid the groundwork for modern mathematical concepts and problem-solving approaches.
在印度，阿耶波多、婆罗摩笈多等数学家在算术、代数和三角学领域取得突破，引入了零和位值制等概念，彻底改变了全球数学思维。这些古代数学传统共同为现代数学概念和解题方法奠定了基础。

Muhammad ibn Musa al-Khwarizmi, Photo Source: Facts.net
穆罕默德·伊本·穆萨·花拉子米

Middle Ages and Renaissance:

中世纪与文艺复兴时期：

During the Middle Ages and Renaissance, mathematics experienced significant advancements in both Europe and the Islamic world. Islamic scholars, including Al-Khwarizmi and Al-Biruni, made groundbreaking contributions to algebra, trigonometry, and geometry during the Islamic Golden Age.
中世纪与文艺复兴时期，欧洲和伊斯兰世界的数学都取得了重大进展。伊斯兰黄金时代，花拉子米、比鲁尼等伊斯兰学者在代数、三角学和几何学领域作出了开创性贡献。

In Europe, the translation of Arabic mathematical texts and the publication of works such as Fibonacci’s “Liber Abaci…” introduced Hindu-Arabic numerals and the decimal system, revolutionizing mathematical computation. The establishment of universities in medieval Europe, such as the University of Bologna and University of Paris, facilitated the exchange of mathematical knowledge and fostered intellectual growth. The invention of the printing press further accelerated the dissemination of mathematical texts, fueling the flourishing of mathematical scholarship during the Renaissance.
在欧洲，阿拉伯数学文献的翻译以及斐波那契《计算之书》等著作的出版，引入了印度-阿拉伯数字和十进制系统，彻底革新了数学计算。中世纪欧洲大学（如博洛尼亚大学、巴黎大学）的建立，促进了数学知识的交流和学术发展。印刷机的发明进一步加速了数学文献的传播，推动了文艺复兴时期数学研究的繁荣。

Mathematicians like Leonardo da Vinci, Nicolaus Copernicus, and Johannes Kepler made significant contributions to geometry, astronomy, and calculus, laying the foundation for modern mathematical thinking and scientific inquiry.
列奥纳多·达·芬奇、尼古拉·哥白尼、约翰尼斯·开普勒等数学家在几何学、天文学和微积分领域作出了重要贡献，为现代数学思维和科学探索奠定了基础。

René Descartes, Photo Source: World History Encyclopedia
勒内·笛卡尔，图片来源：世界历史百科全书

The Enlightenment and Modern Mathematics:

启蒙运动与现代数学

The Enlightenment heralded a period of intellectual and scientific upheaval, catalyzing profound advancements in mathematics that continue to shape the contemporary world. During this Age of Reason, thinkers embraced reason and empiricism, revolutionizing traditional beliefs and ushering in new approaches to mathematics.
启蒙运动开启了思想和科学变革的时代，推动了数学的深刻发展，这些成果至今仍在塑造当代世界。在这个理性时代，思想家们秉持理性主义和经验主义，颠覆了传统观念，开创了数学研究的新路径。

Visionary mathematicians like René Descartes and Pierre de Fermat spearheaded the development of analytic geometry, seamlessly integrating algebra and geometry into a cohesive mathematical framework. Descartes’ innovation of Cartesian coordinates laid the groundwork for modern algebraic geometry, while Fermat’s Last Theorem posed a formidable challenge to number theory.
勒内·笛卡尔、皮埃尔·德·费马等富有远见的数学家率先发展了解析几何，将代数与几何无缝融合成统一的数学框架。笛卡尔发明的笛卡尔坐标系为现代代数几何奠定了基础，而费马大定理则成为数论领域的一大难题。

Simultaneously, the invention of calculus by Isaac Newton and Gottfried Wilhelm Leibniz transformed mathematical understanding, providing potent tools for comprehending change and motion. Calculus revolutionized mechanics, astronomy, and the natural sciences, reshaping our perception of the physical universe. As the $19^{\text{th}}$ and $20^{\text{th}}$ centuries dawned, abstract mathematics emerged as a dominant force, characterized by meticulous formalism and abstraction.
与此同时，艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨发明的微积分，改变了人类对数学的认知，为理解变化和运动提供了强大工具。微积分彻底革新了力学、天文学和自然科学，重塑了我们对物理宇宙的认知。19 世纪和 20 世纪来临之际，抽象数学成为主流，以严谨的形式主义和抽象性为特征。

The Enlightenment and Modern era have witnessed extraordinary advancements in mathematics, from the inception of calculus to the ascent of abstract mathematics and the digital transformation. These milestones have not only deepened our comprehension of the mathematical realm but also expanded the horizons of human knowledge and innovation.
启蒙运动至现代，数学取得了非凡进展——从微积分的诞生到抽象数学的兴起，再到数字化转型。这些里程碑不仅加深了我们对数学领域的理解，也拓展了人类知识与创新的边界。

From basic counting methods to the groundbreaking concepts of calculus and abstract mathematics, each era has contributed to its rich tapestry. As we celebrate Math and Statistics Awareness Month, let’s acknowledge mathematics’ profound impact and embrace its endless possibilities for innovation and understanding.
从基础计数方法到微积分和抽象数学的开创性概念，每个时代都为数学的丰富图景添砖加瓦。在庆祝数学与统计宣传月之际，让我们认可数学的深远影响，拥抱它在创新与认知方面的无限可能。

---

via:

• Surprises from Mathematics Education Research: Student (Mis) use of Mathematical Definitions on JSTOR
  https://www.jstor.org/stable/4145268

• Do names given to math concepts have a role in common mistakes by students?
  https://mathoverflow.net/questions/28612/do-names-given-to-math-concepts-have-a-role-in-common-mistakes-by-students/28614

• Where Did Math Come From? — STEAM Ahead
  https://www.westeamahead.org/blog/2024/4/20/where-did-math-come-from