微积分 | 泰勒级数 / 泰勒展开

注：本文为 “微积分 | 泰勒级数” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

泰勒公式（泰勒展开式）通俗+本质详解

豆沙糕 原创 已于 2025-01-15 14:54:39 修改

泰勒公式的基本概念

泰勒公式，也称泰勒展开式，是利用一个函数在某点的信息，描述其附近取值的公式。若函数足够平滑，在已知该函数在某一点的各阶导数值的情况下，泰勒公式可利用这些导数值作为系数，构建一个多项式近似函数，从而求得该点邻域中的函数值。

泰勒公式的用途可简要概括为：用一个多项式函数去逼近一个给定的函数（即尽量使多项式函数图像拟合给定的函数图像），且逼近需从函数图像上的某个点展开。对于一些复杂函数，若直接求解某点的值存在困难，可通过泰勒公式进行近似求解，这是其应用之一。在机器学习中，泰勒公式主要应用于梯度迭代。

1. 问题的提出

多项式 $P_n(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}+a_n{x}^n$ 是最简单的一类初等函数。由于多项式的运算仅涉及有限项的加减法和乘法，在数值计算方面，多项式是人们乐于使用的工具。因此，我们常采用多项式来近似表达函数，这也是泰勒公式选择多项式函数近似表达给定函数的原因。

2. 近似计算举例

初等数学已揭示了一些函数（如 $\sqrt[5]{x}$、$\lg x$、$\sin x$、$\cos x$、$\arctan x$ 等）的重要性质，但并未说明如何计算这些函数的值。以下以 $f(x)=\cos x$ 的近似计算为例进行说明：

①. 一次（线性）逼近

利用微分近似计算公式 $f(x)\approx f(x_0)+f^{\prime }(x_0)(x-x_0)$（该式由导数/微分的极限表达公式转换得到），对 $x_0=0$ 附近的 $f(x)=\cos x$ 进行线性逼近，可得：$f(x)\approx f(0)+f^{\prime }(0)x$。

由于 $f(0)=\cos 0=1$，$f^{\prime }(0)=-\sin 0=0$，因此 $f(x)=\cos x$ 在 $x_0=0$ 附近的线性逼近函数为 $P_1(x)=1$（如下图所示）。

线性逼近的优点是形式简单、计算方便；缺点是离原点 $O$ 越远，近似度越差。

②. 二次逼近

用二次多项式 $P_2(x)=a_0+a_{1}x+a_2{x}^2$ 逼近 $f(x)=\cos x$ 时，我们期望满足以下条件：

• 在 $x=0$ 处，逼近函数和给定函数的函数值相等，即 $P_2(0)=f(0)=\cos 0=1$，由此可得 $a_0=1$；
• 在 $x=0$ 处，逼近函数和给定函数的斜率相等，即 $P_2^{\prime }(0)=f^{\prime }(0)=-\sin 0=0$，由于 $P_2^{\prime }(x)=a_1+2a_{2}x$，代入 $x=0$ 可得 $a_1=0$；
• 在 $x=0$ 处，逼近函数和给定函数的曲率相等，即 $P_2^{\prime \prime }(0)=f^{\prime \prime }(0)=-\cos 0=-1$，由于 $P_2^{\prime \prime }(x)=2a_2$，代入 $x=0$ 可得 $2a_2=-1$，即 $a_2=-\frac{1}{2}$。

因此，二次逼近函数为 $P_2(x)=1-\frac{1}{2}{x}^2$（如下图所示）。

二次逼近的效果比线性逼近好得多，但仅局限于一定范围（如 $[-\pi ,\pi ]$ 内），超出该范围，图像差异会明显增大。我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值相等，是因为这些值反映了函数（图像）最基本和最主要的性质，这些性质的逼近可使两个函数更接近（从函数图像可直观看出）。

③. 八次逼近

用八次多项式 $P_8(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_8{x}^8$ 逼近 $f(x)=\cos x$ 时，我们期望满足：

• 在 $x=0$ 处，逼近函数和给定函数的函数值相等，即 $P_8(0)=f(0)=\cos 0=1$，可得 $a_0=1$；
• 在 $x=0$ 处，逼近函数和给定函数的斜率相等，即 $P_8^{\prime }(0)=f^{\prime }(0)=-\sin 0=0$，可得 $a_1=0$；
• 更高阶导数在 $x=0$ 处相等，以保证曲率等更细致的性质一致。

通过计算可得：$\cos x\approx P_8(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}$（如下图所示）。

八次逼近（绿色图像）比二次逼近（蓝色图像）在更大范围内更接近余弦函数（红色图像）。

由上述三次不同程度的函数逼近可知：当对精确度要求较高且需要估计误差时，必须使用高次多项式来近似表达函数，同时给出误差公式。以上即为利用多项式函数逼近给定函数的过程。

3. 泰勒公式的推导

给定一个函数 $f(x)$，需寻找一个在指定点 $x_0$ 附近与 $f(x)$ 很近似的多项式函数 $P_n(x)$，记为：$P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0{)}^2+\cdots +a_n(x-x_0{)}^n$，使得 $P_n(x)$ 与 $f(x)$ 近似，且两者的误差 $R_n(x)=f(x)-P_n(x)$ 可估计。

从几何角度看，$P_n(x)$ 和 $f(x)$ 代表两条曲线，要使它们在 $x_0$ 附近靠近，需满足以下条件：

1. 两曲线在 $x_0$ 点相交，即 $P_n(x_0)=f(x_0)$；
2. 两曲线在 $x_0$ 点相切（相切比仅相交更接近），即 $P_n^{\prime }(x_0)=f^{\prime }(x_0)$；
3. 两曲线在 $x_0$ 点弯曲方向相同（弯曲方向相同比相反更接近），即 $P_n^{\prime \prime }(x_0)=f^{\prime \prime }(x_0)$；
4. 推而广之，若在 $x_0$ 附近的更高阶导数也相等，即 $P_n^{(k)}(x_0)=f^{(k)}(x_0)$（$k=1,2,\cdots ,n$），则近似程度会越来越好。

综上，所要寻找的多项式需满足下列条件：
$$\begin{array}{rl}{P}_n(x_0)& =f(x_0)\\ P_n^{\prime }(x_0)& =f^{\prime }(x_0)\\ P_n^{\prime \prime }(x_0)& =f^{\prime \prime }(x_0)\\ & ⋮\\ P_n^{(n)}(x_0)& =f^{(n)}(x_0)\end{array}$$

对多项式 $P_n(x)$ 求各阶导数并代入 $x_0$，可求解系数 $a_k$：

• 由 $P_n(x_0)=a_0=f(x_0)$，得 $a_0=f(x_0)$；
• 由 $P_n^{\prime }(x_0)=a_1=f^{\prime }(x_0)$，得 $a_1=f^{\prime }(x_0)$；
• 由 $P_n^{\prime \prime }(x_0)=2!a_2=f^{\prime \prime }(x_0)$，得 $a_2=\frac{1}{2!}{f}^{\prime \prime }(x_0)$；
• 由 $P_n^{(3)}(x_0)=3!a_3=f^{(3)}(x_0)$，得 $a_3=\frac{1}{3!}{f}^{(3)}(x_0)$；
• $⋮$
• 由 $P_n^{(n)}(x_0)=n!a_n=f^{(n)}(x_0)$，得 $a_n=\frac{1}{n!}{f}^{(n)}(x_0)$。

由此，多项式函数 $P_n(x)$ 的系数可全部由 $f(x)$ 在 $x_0$ 处的各阶导数表示，即：
$$P_n(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n$$

由于是用多项式函数无限逼近给定函数，两者之间必然存在微小误差 $f\left(x\right)-P_n\left(x\right)$，该误差记为 $R_n(x)$。

4. 泰勒公式的定义

若函数 $f(x)$ 在含 $x_0$ 的某个开区间 $(a,b)$ 内具有直到 $n+1$ 阶导数，则 $\forall x\in (a,b)$，有：

$$f(x)=\frac{f\left(x_0\right)}{0!}+\frac{f^{\prime }\left(x_0\right)}{1!}\left(x-x_0\right)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\cdots +\frac{f^{(n)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n+R_n(x)$$
即
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)$$

其中，余项（即误差）$R_n(x)=\frac{f^{(n+1)}(\xi )}{(n+1)!}(x-x_0{)}^{n+1}$，$\xi$ 是介于 $x_0$ 与 $x$ 之间的某个值。

泰勒公式的余项有多种表达方式，上述形式称为 $n$ 阶泰勒展开式的拉格朗日余项。拉格朗日余项可理解为 $n$ 阶泰勒公式多展开一阶（即 $n$ 变为 $n+1$）。注意，这里的余项即为误差。由于使用多项式函数在某点展开逼近给定函数时，必然存在微小误差，因此将该误差称为余项。

5. 扩展——麦克劳林公式

麦克劳林公式是泰勒公式的一种特殊情况，即当 $x_0=0$ 时的泰勒公式。将 $x_0=0$ 代入泰勒公式，可得：
$$f(x)=f(0)+\frac{f^{\prime }(0)}{1!}x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n+R_n(x)$$

几个常见初等函数的带有佩亚诺余项的麦克劳林公式

• $e^x=1+x+\frac{1}{2!}{x}^2+\cdots +\frac{1}{n!}{x}^n+o(x^n)$
• $\sin x=x-\frac{1}{3!}{x}^3+\cdots +\frac{(-1{)}^{m-1}}{(2m-1)!}{x}^{2m-1}+o(x^{2m-1})$
• $\cos x=1-\frac{1}{2!}{x}^2+\frac{1}{4!}{x}^4-\cdots +\frac{(-1{)}^m}{(2m)!}{x}^{2m}+o(x^{2m})$
• $\ln (1+x)=x-\frac{1}{2}{x}^2+\frac{1}{3}{x}^3-\cdots +\frac{(-1{)}^{n-1}}{n}{x}^n+o(x^n)$

佩亚诺余项为 $(x-x_0{)}^n$ 的高阶无穷小，即 $R_n(x)=o[(x-x_0{)}^n]$。

---

数学基础 – 泰勒展开式

sz66cm 原创 已于 2024-07-23 10:56:52 修改

泰勒展开

泰勒展开是一种将函数在某点附近展开成幂级数的数学工具。具体而言，对于在某点 $a$ 处具有 $n$ 阶导数的函数 $f(x)$，其泰勒展开式为：

$$f(x)=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+\cdots +\frac{f^{(n)}(a)}{n!}(x-a{)}^n+R_n(x)(x\in \text{收敛区间})$$

其中，$R_n(x)$ 是余项，用于表示级数截断后与实际函数之间的误差。对于某些函数，当 $n$ 趋近于无穷大时，余项趋近于零，泰勒级数就可以完全表示函数。

泰勒展开的前置条件

泰勒展开需要满足以下条件：

1. 函数的可微性
   函数在展开点附近必须具有足够高阶的导数。若希望展开到 $n$ 阶，则函数必须在该点具有至少 $n$ 阶的导数。

2. 函数的收敛性
   泰勒级数的收敛性依赖于函数的性质及展开点的位置。通常情况下，函数在展开点附近必须解析（即在该点及其附近有无穷多个导数且导数连续）。

3. 展开点的选择
   泰勒展开是在某个点 $a$ 附近进行的，因此需要选择一个合适的展开点 $a$。通常选择函数在该点及其附近解析的点。

泰勒展开的一般形式为：

$$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n(x\in \text{收敛区间})$$

其中 $f^{(n)}(a)$ 表示函数 $f(x)$ 在点 $a$ 处的第 $n$ 阶导数。

在实际应用中，通常考虑泰勒级数的前几项，忽略高阶小项，以得到函数在展开点附近的近似表达式。

例子 1：$e^x$ 在 $x=0$ 处的泰勒展开

对于指数函数 $e^x$，所有阶导数均为 $e^x$，在 $x=0$ 处，所有导数值均为 1。因此，其泰勒展开式为：

$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots (x\in \mathbb{R})$$

这实际上是 $e^x$ 的麦克劳林级数（泰勒级数的特殊情况，展开点 $a=0$）。

例子 2：$\sin (x)$ 在 $x=0$ 处的泰勒展开

对于正弦函数 $\sin (x)$，其奇数阶导数在 $x=0$ 处为 $\pm 1$，偶数阶导数为 0。因此，其泰勒展开式为：

$$\sin (x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots (x\in \mathbb{R})$$

同样，这也是 $\sin (x)$ 的麦克劳林级数。

例子 3：$\ln (1+x)$ 在 $x=0$ 处的泰勒展开

对于自然对数函数 $\ln (1+x)$，其 $n$ 阶导数在 $x=0$ 处为 $(-1{)}^{n+1}(n-1)!$。因此，其泰勒展开式为：

$$\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots (|x|<1)$$

总结

泰勒展开是一种强大的数学工具，它将复杂的函数表达为幂级数的形式，从而在某个点附近近似该函数。这在数值分析、物理学和工程学中有广泛应用，可以用来逼近函数值、解决微分方程、计算积分等。

了解泰勒展开的基本原理和一些典型函数的展开式，对于深入理解和应用数学分析具有重要意义。

---

常见函数的泰勒级数展开

二分掌柜的 于 2024-07-14 13:48:47 发布

flyfish

1. 指数函数

1. 指数函数
   $$e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots (x\in \mathbb{R})$$

2. 三角函数

1. 正弦函数
   $$\sin x=\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots (x\in \mathbb{R})$$
2. 余弦函数
   $$\cos x=\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots (x\in \mathbb{R})$$
3. 正切函数
   $$\tan x=\sum _{n=1}^{\infty }\frac{B_{2n}(-4{)}^n(1-4^n)}{(2n)!}{x}^{2n-1}=x+\frac{1}{3}{x}^3+\frac{2}{15}{x}^5+\frac{17}{315}{x}^7+\cdots \left(x\in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)\right)$$

3. 反三角函数

1. 反正弦函数
   $$\arcsin x=\sum _{n=0}^{\infty }\frac{(2n)!}{4^n(n!{)}^2(2n+1)}{x}^{2n+1}=x+\frac{1}{6}{x}^3+\frac{3}{40}{x}^5+\frac{5}{112}{x}^7+\cdots (|x|<1)$$
2. 反正切函数
   $$\arctan x=\sum _{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{2n+1}=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots (|x|\le 1)$$

4. 对数函数

1. 自然对数函数
   $$\ln (1+x)=\sum _{n=1}^{\infty }(-1{)}^{n+1}\frac{x^n}{n}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots (|x|<1)$$
2. 对数函数在 ( x = 1 ) 处展开
   $$\ln x=\sum _{n=1}^{\infty }(-1{)}^{n+1}\frac{(x-1{)}^n}{n}=(x-1)-\frac{(x-1{)}^2}{2}+\frac{(x-1{)}^3}{3}-\frac{(x-1{)}^4}{4}+\cdots (0<x\le 2)$$

5. 双曲函数

1. 双曲正弦函数
   $$\sinh x=\sum _{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots (x\in \mathbb{R})$$
2. 双曲余弦函数
   $$\cosh x=\sum _{n=0}^{\infty }\frac{x^{2n}}{(2n)!}=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots (x\in \mathbb{R})$$
3. 双曲正切函数
   $$\tanh x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots (x\in \mathbb{R})$$

6. 幂函数

1. 幂函数（广义二项式定理）
   $$(1+x{)}^k=\sum _{n=0}^{\infty }(\genfrac{}{}{0ex}{}{k}{n})x^n=1+kx+\frac{k(k-1)}{2!}{x}^2+\frac{k(k-1)(k-2)}{3!}{x}^3+\cdots (|x|<1)$$
2. 幂函数的另一种形式
   $$(1+x{)}^{\alpha }=1+\alpha x+\frac{\alpha (\alpha -1)}{2!}{x}^2+\cdots (|x|<1)$$

7. 几何级数

1. 几何级数
   $$\frac{1}{1-x}=\sum _{n=0}^{\infty }{x}^n=1+x+x^2+x^3+x^4+\cdots (|x|<1)$$
2. 几何级数的交错形式
   $$\frac{1}{1+x}=\sum _{n=0}^{\infty }(-1{)}^n{x}^n=1-x+x^2-x^3+x^4-\cdots (|x|<1)$$

8. 反双曲函数

1. 反双曲正切函数
   $$\text{artanh}(x)=\sum _{n=0}^{\infty }\frac{x^{2n+1}}{2n+1}=x+\frac{x^3}{3}+\frac{x^5}{5}+\cdots (|x|<1)$$
2. 反双曲余弦函数
   $$\text{arcosh}(x)=\ln \left(x+\sqrt{x^2-1}\right)(x\ge 1)$$

9. 其他函数

1. 反正切函数的另一种形式
   $$\arctan x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots (|x|\le 1)$$
2. 自然对数函数的另一种形式
   $$\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots (|x|<1)$$
3. 反正弦函数的另一种形式
   $$\arcsin x=x+\frac{1}{6}{x}^3+\frac{3}{40}{x}^5+\frac{5}{112}{x}^7+\cdots (|x|<1)$$

---

泰勒公式常见函数展开

陌雨’ 已于 2024-08-16 22:57:20 修改

1. 指数函数

$$\begin{array}{rl}{e}^x& =\sum _{n=0}^{\infty }\frac{1}{n!}{x}^n\\ & =1+x+\frac{1}{2!}{x}^2+\cdots \\ & x\in (-\infty ,+\infty )\end{array}$$

2. 三角函数

正弦函数

$$\begin{array}{rl}\sin x& =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}\\ & =x-\frac{1}{3!}{x}^3+\frac{1}{5!}{x}^5+\cdots \\ & x\in (-\infty ,+\infty )\end{array}$$

余弦函数

$$\begin{array}{rl}\cos x& =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n)!}{x}^{2n}\\ & =1-\frac{1}{2!}{x}^2+\frac{1}{4!}{x}^4+\cdots \\ & x\in (-\infty ,+\infty )\end{array}$$

正切函数

$$\begin{array}{rl}\tan x& =\sum _{n=1}^{\infty }\frac{B_{2n}(-4{)}^n(1-4^n)}{(2n)!}{x}^{2n-1}\\ & =x+\frac{1}{3}{x}^3+\frac{2}{15}{x}^5+\frac{17}{315}{x}^7+\cdots \\ & x\in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)\end{array}$$

3. 反三角函数

反正弦函数

$$\begin{array}{rl}\arcsin x& =\sum _{n=0}^{\infty }\frac{(2n)!}{4^n(n!{)}^2(2n+1)}{x}^{2n+1}\\ & =x+\frac{1}{6}{x}^3+\frac{3}{40}{x}^5+\frac{5}{112}{x}^7+\cdots \\ & x\in (-1,1)\end{array}$$

反正切函数

$$\begin{array}{rl}\arctan x& =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{2n+1}{x}^{2n+1}\\ & =x-\frac{1}{3}{x}^3+\frac{1}{5}{x}^5+\cdots \\ & x\in [-1,1]\end{array}$$

4. 对数函数

$$\begin{array}{rl}\ln (1+x)& =\sum _{n=1}^{\infty }\frac{(-1{)}^{n+1}}{n}{x}^n\\ & =x-\frac{1}{2}{x}^2+\frac{1}{3}{x}^3-\frac{1}{4}{x}^4+\cdots \\ & x\in (-1,1]\end{array}$$

5. 几何级数

几何级数 (正项)

$$\begin{array}{rl}\frac{1}{1-x}& =\sum _{n=0}^{\infty }{x}^n\\ & =1+x+x^2+x^3+\cdots \\ & x\in (-1,1)\end{array}$$

几何级数 (交错项)

$$\begin{array}{rl}\frac{1}{1+x}& =\sum _{n=0}^{\infty }(-1{)}^n{x}^n\\ & =1-x+x^2-x^3+\cdots \\ & x\in (-1,1)\end{array}$$

6. 幂函数

$$\begin{array}{rl}(1+x{)}^{\alpha }& =\sum _{n=0}^{\infty }\left(\genfrac{}{}{0ex}{}{\alpha }{n}\right)x^n\\ & =1+\alpha x+\frac{\alpha (\alpha -1)}{2!}{x}^2+\cdots \\ & x\in (-1,1)\end{array}$$

---

泰勒展开式（常见）

debug_running_Hu 已于 2024-11-17 09:30:05 修改

让我们详细讨论一些常见函数在 $x=0$ 处的泰勒展开式（也称为麦克劳林展开式）。泰勒展开式是将一个函数在某一点附近用无限多项式逼近的方法。麦克劳林展开式是泰勒展开式的一个特例，即展开点为 $x=0$。

展开式的形式为：

$$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(0)}{n!}{x}^n=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3+\dots$$

其中，$f^{(n)}(0)$ 表示函数 $f(x)$ 在 $x=0$ 处的 $n$ 阶导数。

以下是一些常见函数在 $x=0$ 处的麦克劳林展开式，以及它们的推导思路：

常见函数的麦克劳林展开式（泰勒展开式在 $x=0$ 处的特例）

泰勒展开式是将函数在某一点附近用无限多项式逼近的方法，当展开点为 $x=0$ 时，称为麦克劳林展开式，其一般形式为：

$$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(0)}{n!}{x}^n=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3+\dots$$

其中， $f^{(n)}(0)$ 表示函数 $f(x)$ 在 $x=0$ 处的 $n$ 阶导数。以下是常见函数的麦克劳林展开式及推导思路：

一、指数函数

1. 基本指数函数 $e^x$

展开式：
$$e^x=\sum _{n=0}^{\infty }\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\dots (x\in \mathbb{R})$$
推导：
指数函数的各阶导数均为自身，即 $f^{(n)}(x)=e^x$ ，在 $x=0$ 处的所有阶导数都等于1。代入泰勒展开式公式即可得到结果，该级数收敛于全体实数 $x$ 。

2. 指数函数的推广形式 $e^{ax}$

展开式：
$$e^{ax}=\sum _{n=0}^{\infty }\frac{(ax{)}^n}{n!}=1+ax+\frac{(ax{)}^2}{2!}+\frac{(ax{)}^3}{3!}+\dots (x\in \mathbb{R})$$
推导：
将 $e^x$ 的麦克劳林展开式中的 $x$ 替换为 $ax$ 即可，该级数收敛于全体实数 $x$ 。

二、三角函数

1. 正弦函数 $\sin x$

展开式：
$$\sin x=\sum _{n=0}^{\infty }\frac{(-1{)}^n{x}^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots (x\in \mathbb{R})$$
推导：
$\sin x$ 的导数依次为 $\cos x$ ， $-\sin x$ ， $-\cos x$ ， $\sin x$ …在 $x=0$ 处，这些导数的值依次为1, 0, -1, 0, 1, 0, …代入泰勒展开式后，只留下奇数项，得到上述结果，该级数收敛于全体实数 $x$ 。

2. 余弦函数 $\cos x$

展开式：
$$\cos x=\sum _{n=0}^{\infty }\frac{(-1{)}^n{x}^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots (x\in \mathbb{R})$$
推导：
类似于 $\sin x$ ， $\cos x$ 的导数在 $x=0$ 处的值依次为0, -1, 0, 1, 0, -1,…代入泰勒展开式后，只留下偶数项，得到上述结果，该级数收敛于全体实数 $x$ 。

3. 正切函数 $\tan x$

展开式：
$$\tan x=x+\frac{x^3}{3}+\frac{2x^5}{15}+\frac{17x^7}{315}+\dots \left(|x|<\frac{\pi }{2}\right)$$
推导：
该级数通过重复求 $\tan x$ 的导数并在 $x=0$ 处求值得到，系数会越来越复杂。由于 $\tan x$ 在 $\frac{\pi }{2}$ 的奇数倍处有垂直渐近线，因此该级数在 $|x|<\frac{\pi }{2}$ 的区间内收敛。

4. 余切函数 $\cot x$

展开式：
$$\cot x=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\frac{2x^5}{945}-\dots (0<|x|<\pi )$$
推导：
与正切函数类似，通过重复求导得到。注意到 $\frac{1}{x}$ 项的存在，表明 $\cot x$ 在 $x=0$ 处存在奇点（极点），因此这是一个洛朗级数（非严格意义上的麦克劳林级数），在 $0<|x|<\pi$ 的区间内收敛。

5. 正割函数 $\sec x$

展开式：
$$\sec x=1+\frac{x^2}{2}+\frac{5x^4}{24}+\frac{61x^6}{720}+O(x^8)\left(|x|<\frac{\pi }{2}\right)$$
推导：
正割函数的高阶导数计算复杂，展开式仅给出前几项，其中 $O(x^8)$ 表示被省略的项的阶数不低于 $x^8$ 。其收敛半径为 $\frac{\pi }{2}$ ，即级数在 $|x|<\frac{\pi }{2}$ 内收敛。

6. 余割函数 $\csc x$

展开式：
$$\csc x=\frac{1}{x}+\frac{x}{6}+\frac{7x^3}{360}+O(x^5)(0<|x|<\pi )$$
推导：
类似于正割函数，余割函数在 $x=0$ 处无定义，展开式包含 $\frac{1}{x}$ 项以表示其在 $x=0$ 附近的奇异性，收敛半径为 $\pi$ ，即级数在 $0<|x|<\pi$ 内收敛。

7. 正割平方函数 ${\sec }^{2}x$

展开式：
$${\sec }^{2}x=1+x^2+\frac{2x^4}{3}+\frac{17x^6}{45}+\dots \left(|x|<\frac{\pi }{2}\right)$$
推导：
可通过对 ${\sec }^{2}x$ 重复求导，或利用 ${\sec }^{2}x=1+{\tan }^{2}x$ 及 $\tan x$ 的麦克劳林展开式推导，其收敛区间为 $|x|<\frac{\pi }{2}$ 。

8. 利用三角恒等式推导其他展开式

已知三角函数展开式后，可结合三角恒等式推导更多函数的展开式。例如，由 $\sin (2x)=2\sin x\cos x$ ，将 $\sin x$ 和 $\cos x$ 的麦克劳林展开式代入并整理，即可得到 $\sin (2x)$ 的麦克劳林展开式。

三、反三角函数

反正切函数 $\arctan x$

展开式：
$$\arctan x=\sum _{n=0}^{\infty }\frac{(-1{)}^n{x}^{2n+1}}{2n+1}=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\dots (|x|\le 1)$$
推导：
对 $\arctan x$ 求导得 $\frac{1}{1+x^2}$ ，利用几何级数展开式后积分，可得到 $\arctan x$ 的展开式，该级数在区间 $[-1,1]$ 上收敛。

四、对数函数

自然对数 $\ln (1+x)$

展开式：
$$\ln (1+x)=\sum _{n=1}^{\infty }\frac{(-1{)}^{n+1}{x}^n}{n}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\dots (-1<x\le 1)$$
推导：
通过计算 $\ln (1+x)$ 的各阶导数并在 $x=0$ 处求值得到，该展开式在 $-1<x\le 1$ 的区间内收敛。

五、双曲函数

1. 双曲正弦函数 $\sinh x$

展开式：
$$\sinh x=\sum _{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\dots (x\in \mathbb{R})$$
推导：

双曲正弦函数定义为 $\sinh x=\frac{e^x-e^{-x}}{2}$ ，利用 $e^x$ 的麦克劳林展开式可推导出其展开式，该级数收敛于全体实数 $x$ 。

2. 双曲余弦函数 $\cosh x$

展开式：
$$\cosh x=\sum _{n=0}^{\infty }\frac{x^{2n}}{(2n)!}=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\dots (x\in \mathbb{R})$$
推导：

双曲余弦函数定义为 $\cosh x=\frac{e^x+e^{-x}}{2}$ ，类似于 $\sinh x$ ，利用 $e^x$ 的麦克劳林展开式可推导得到，该级数收敛于全体实数 $x$ 。

六、幂函数与几何级数

1. 几何级数 $\frac{1}{1-x}$

展开式：
$$\frac{1}{1-x}=\sum _{n=0}^{\infty }{x}^n=1+x+x^2+x^3+x^4+\dots (|x|<1)$$
推导：

可视为等比数列求和公式的极限形式，该级数仅在 $|x|<1$ 的区间内收敛。

2. 幂函数 $(1+x{)}^r$ （广义二项式定理）

展开式：
$$(1+x{)}^r=\sum _{n=0}^{\infty }(\genfrac{}{}{0ex}{}{r}{n})x^n=1+rx+\frac{r(r-1)}{2!}{x}^2+\frac{r(r-1)(r-2)}{3!}{x}^3+\dots (|x|<1)$$
推导：

其中 $\left(\genfrac{}{}{0ex}{}{r}{n}\right)=\frac{r(r-1)\cdots (r-n+1)}{n!}$ 为广义二项式系数。当 $r$ 为非负整数时，展开式为有限项（普通二项式定理）；当 $r$ 为其他实数时，级数在 $|x|<1$ 收敛。该展开式包含多种特例（如令 $r=-1$ 可得到几何级数展开式）。

七、其他函数

1. 误差函数 $\text{erf}(x)$ 的近似

近似展开式：
$$\text{erf}(x)\approx \frac{2}{\sqrt{\pi }}\left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\dots \right)(x\in \mathbb{R})$$
说明：

误差函数定义为 $\text{erf}(x)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t^2}dt$ ，上述为其麦克劳林展开式的前几项，完整展开式较复杂，该级数收敛于全体实数 $x$ 。

总结

1. 上述展开式仅在其收敛区间内有效，超出区间时级数发散。
2. 实际应用中，通常取展开式的前几项进行近似计算，项数需根据精度要求选择。
3. 利用函数的导数、积分、变量替换或恒等式，可由已知展开式推导更多函数的泰勒级数展开式。

---

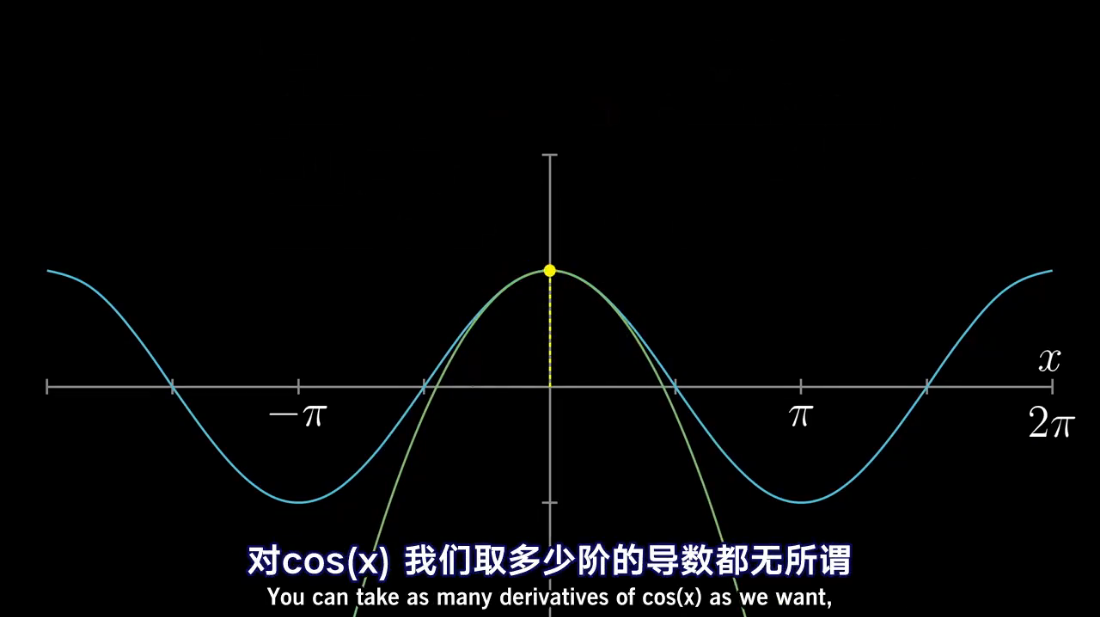
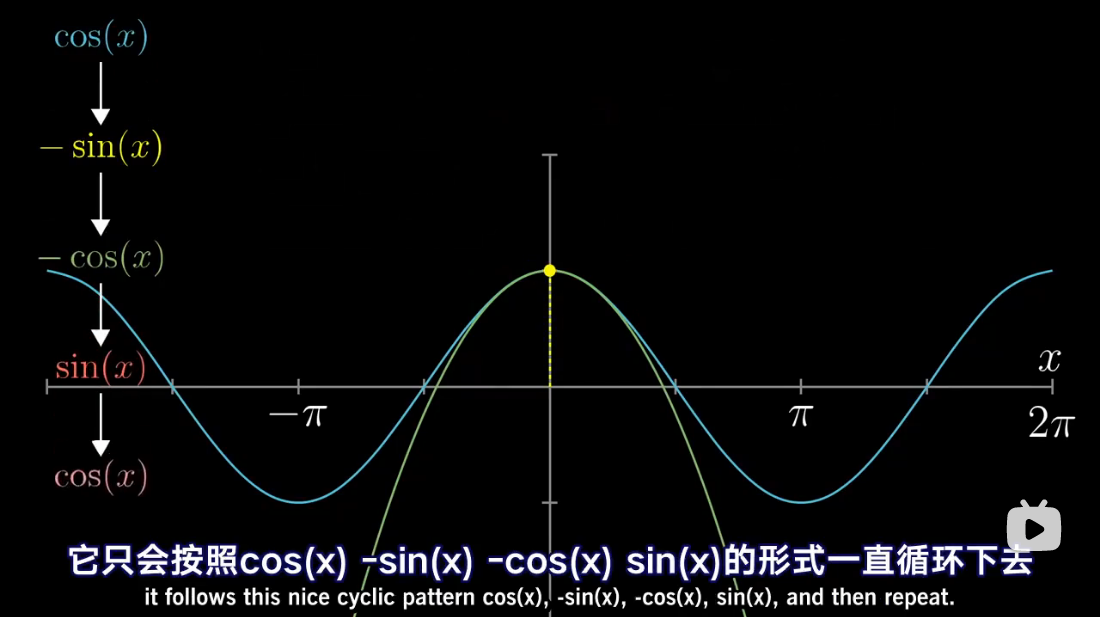
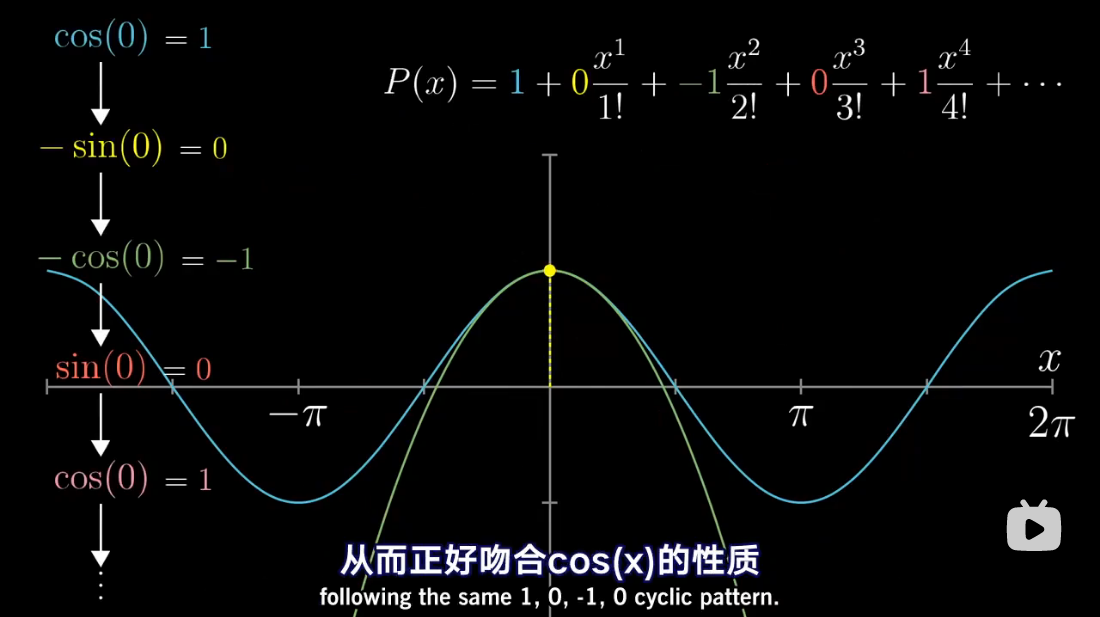
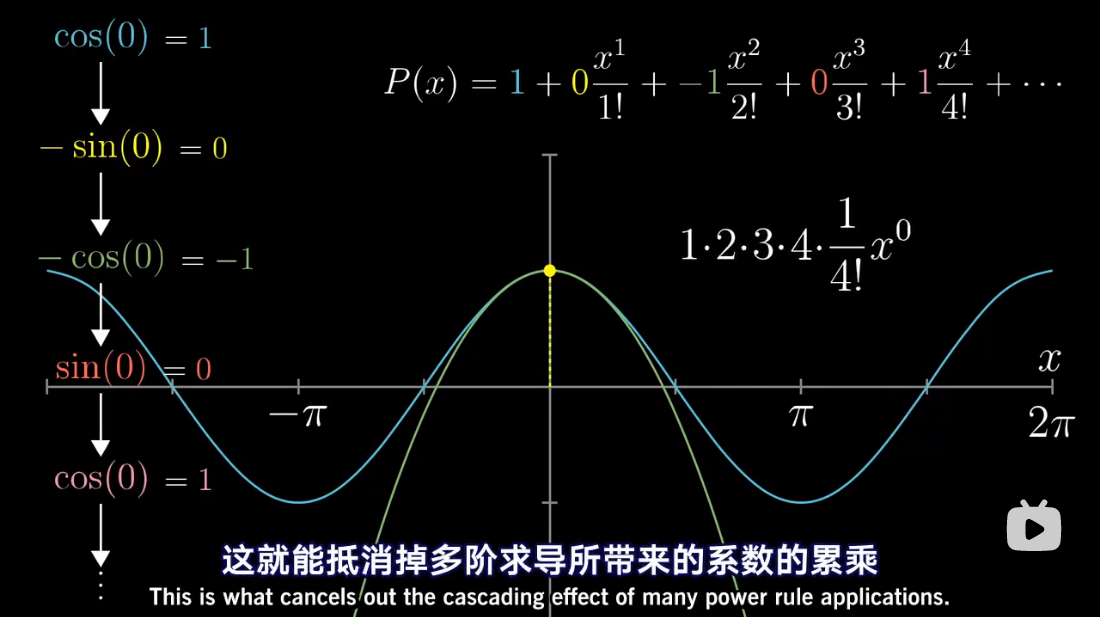
图解泰勒展开

 

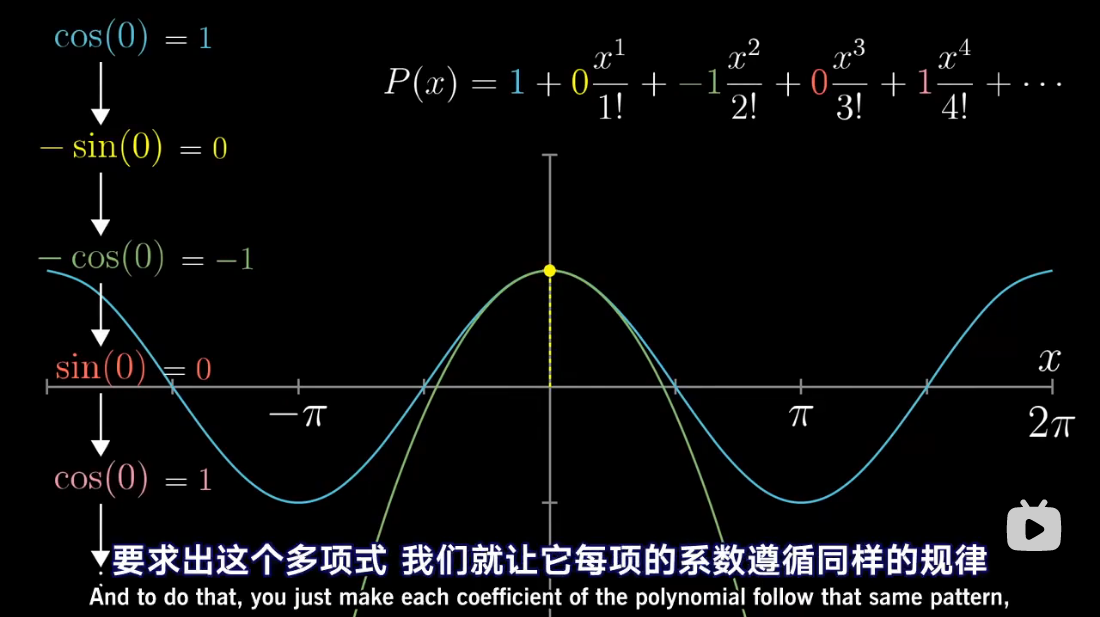
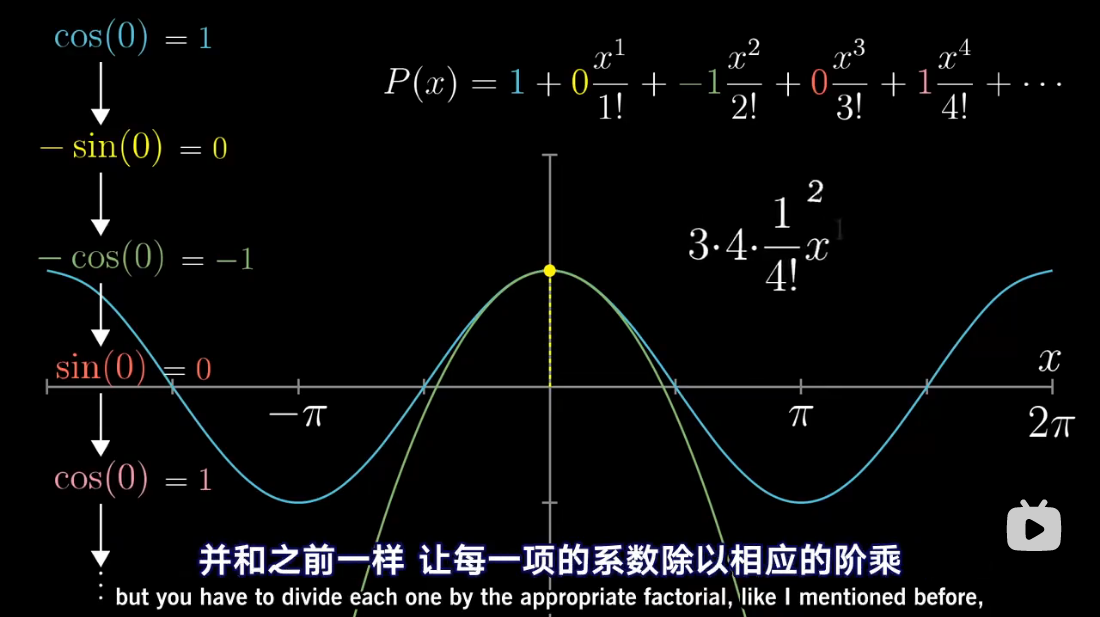
累乘抵消

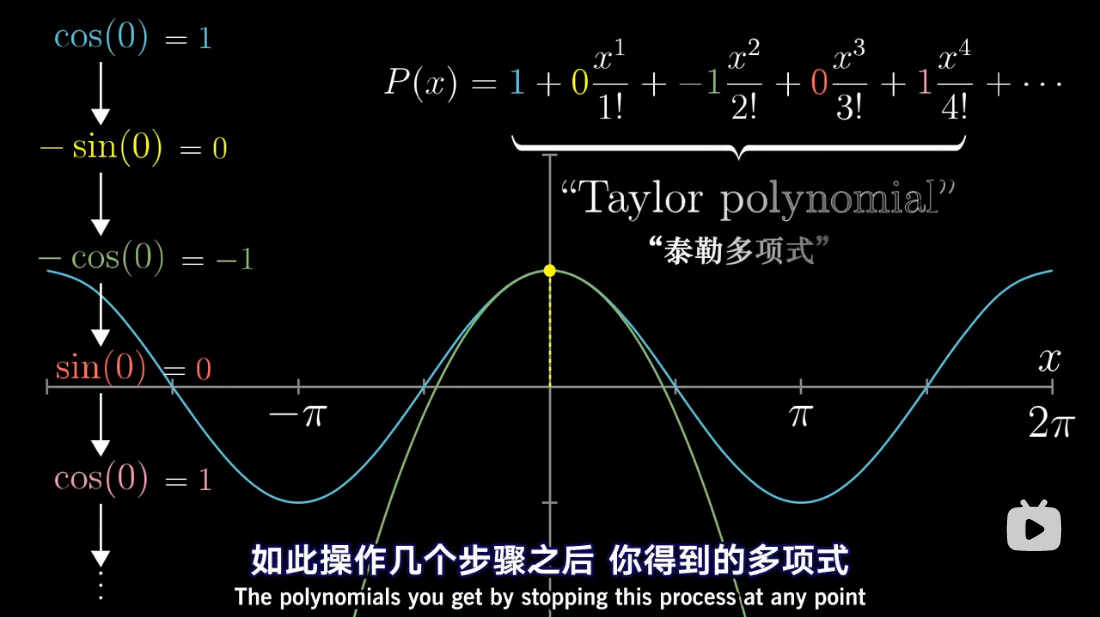
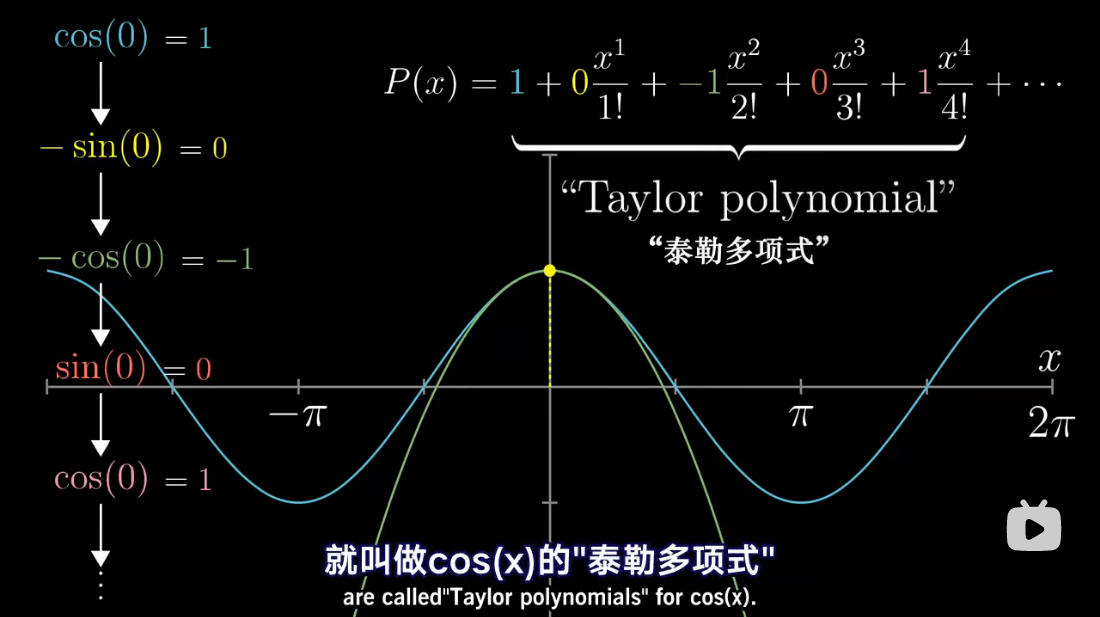
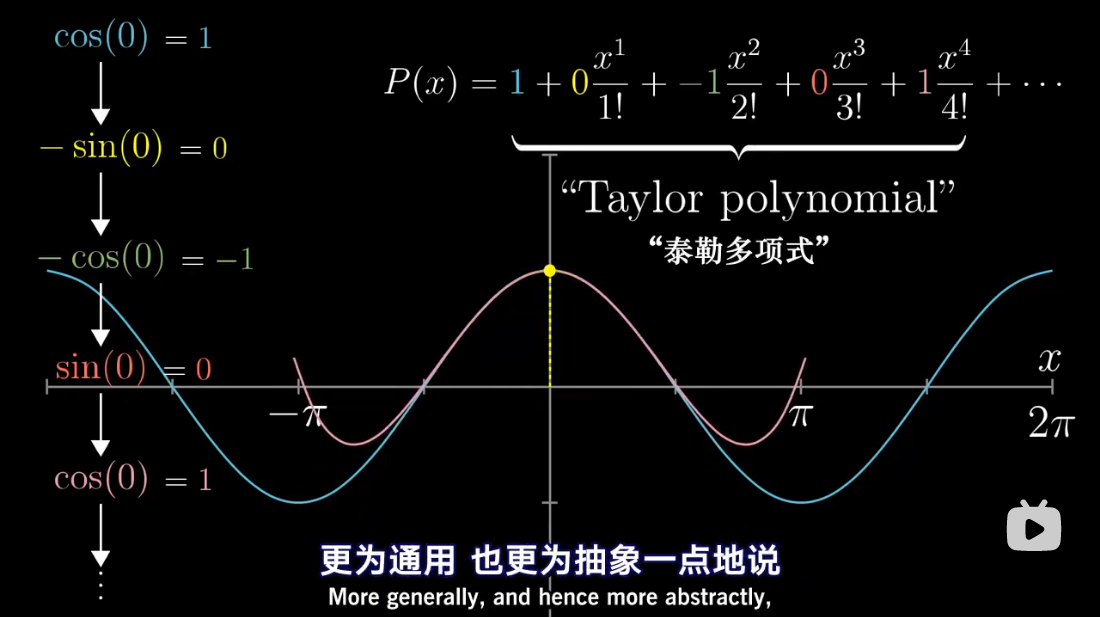
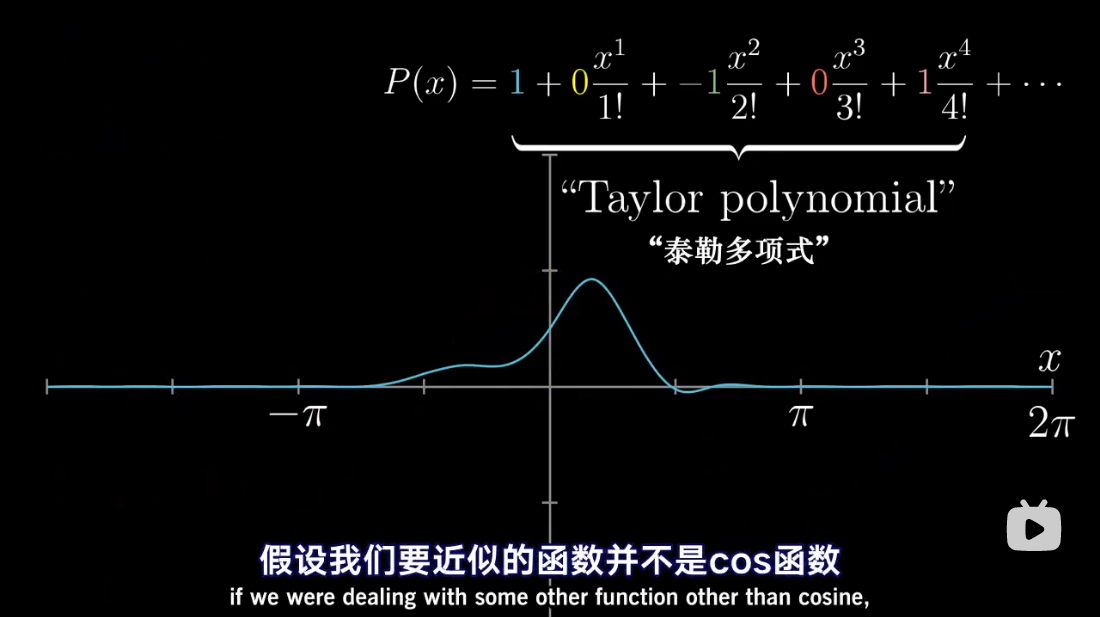
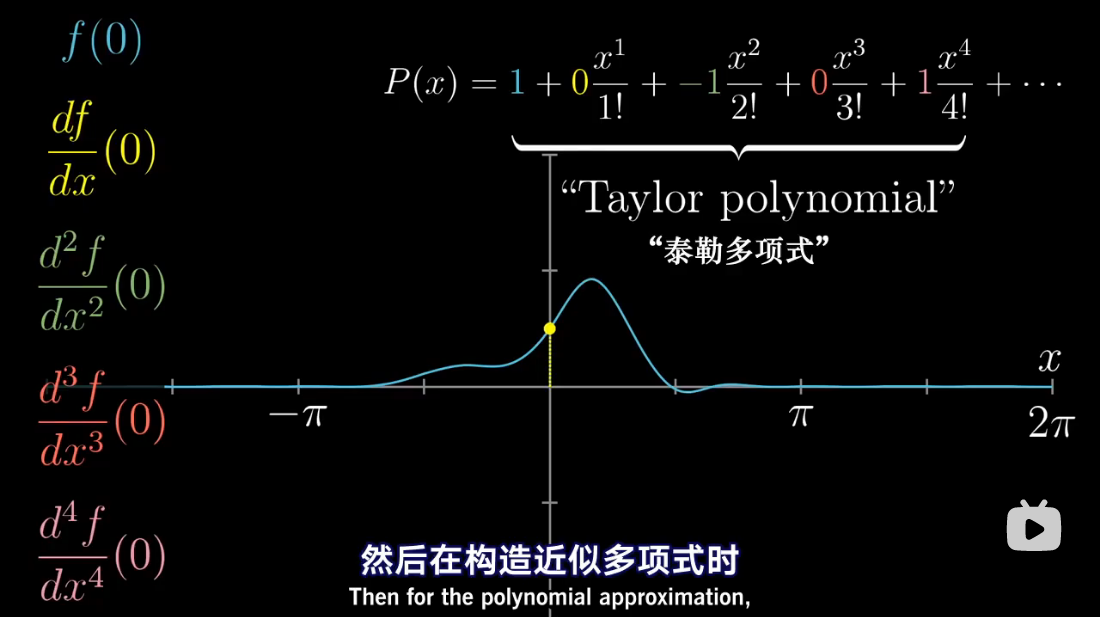
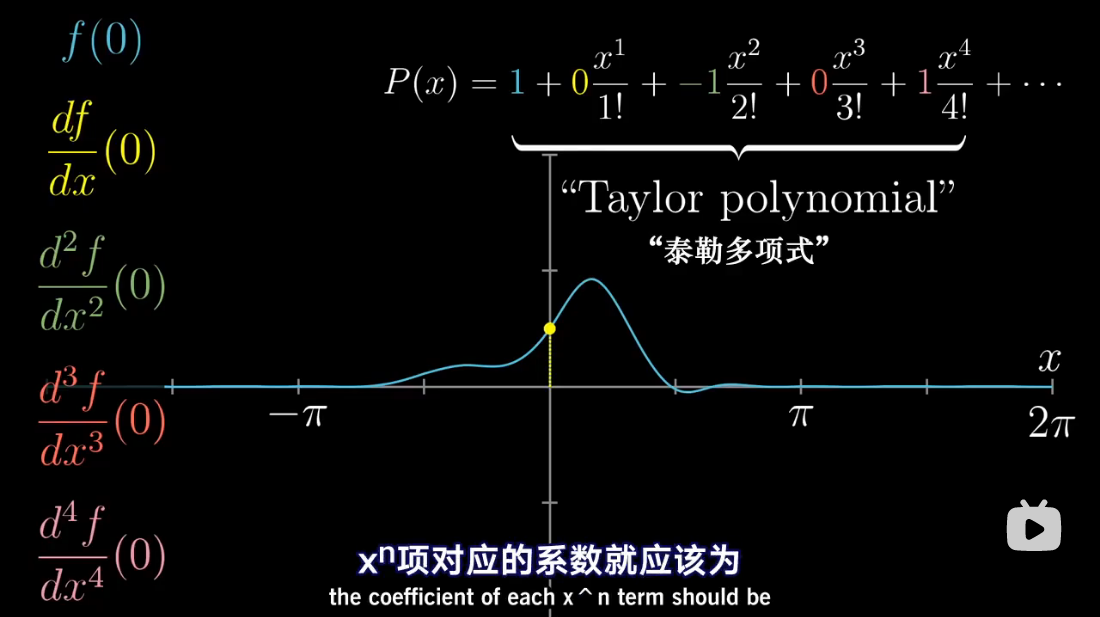
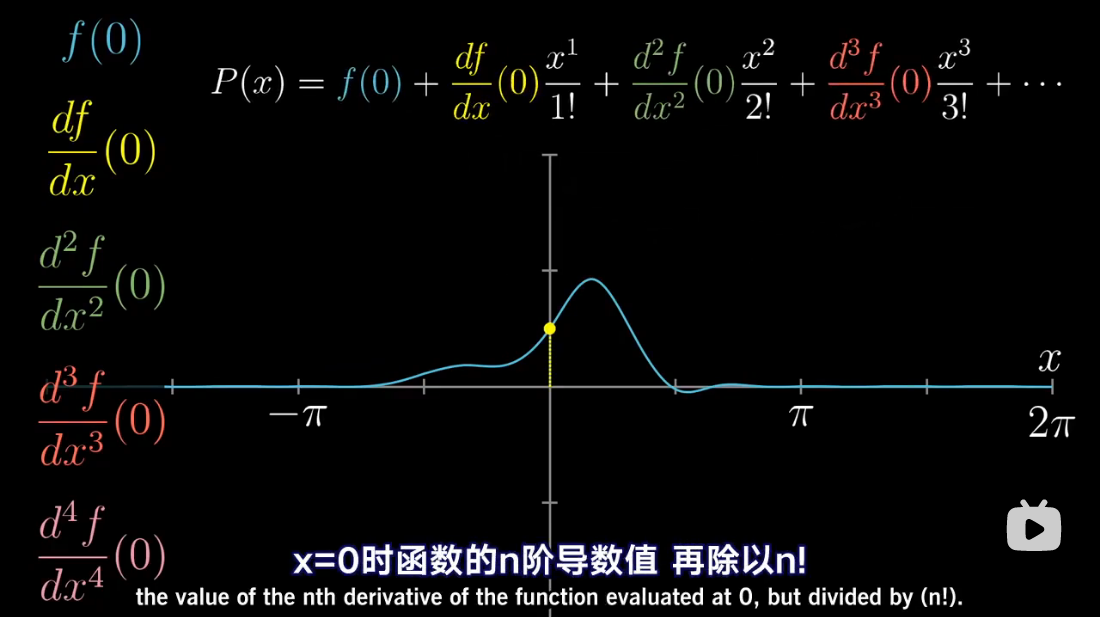
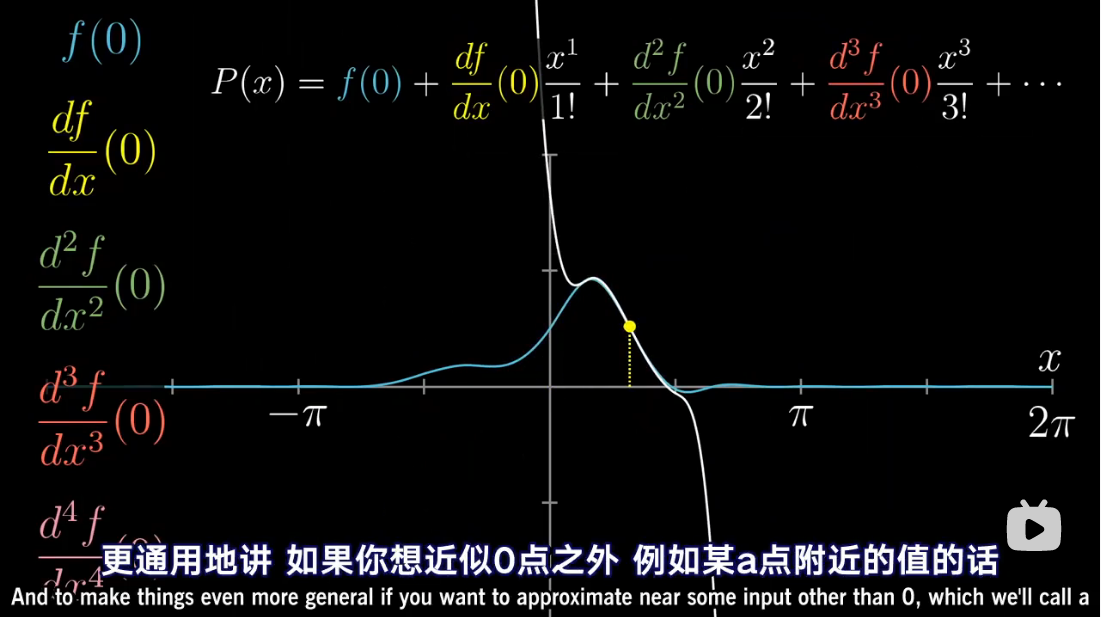
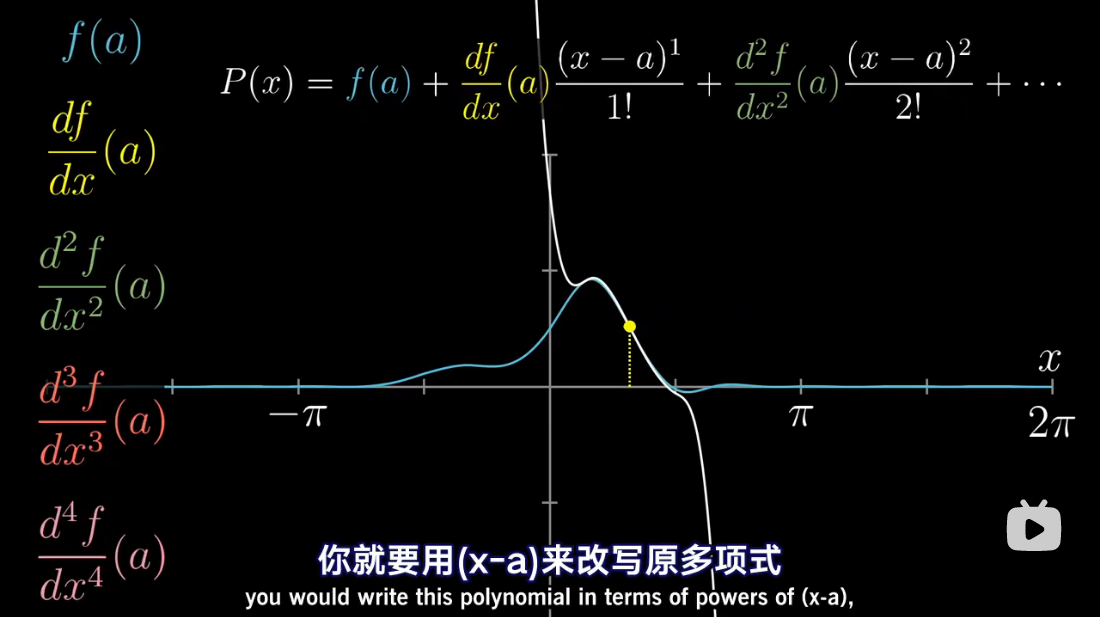
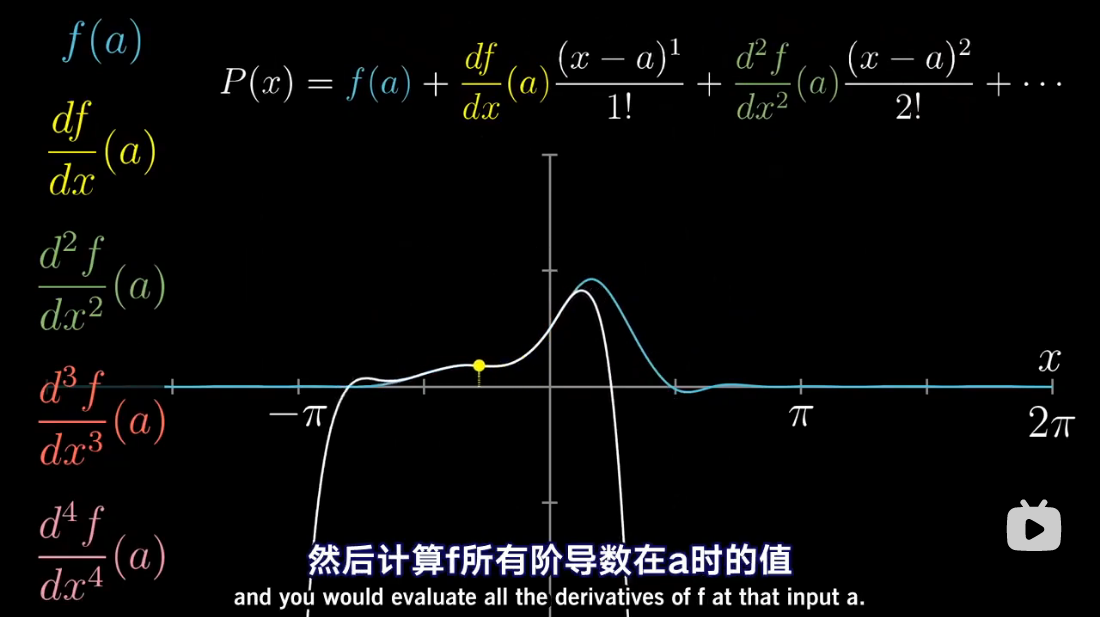
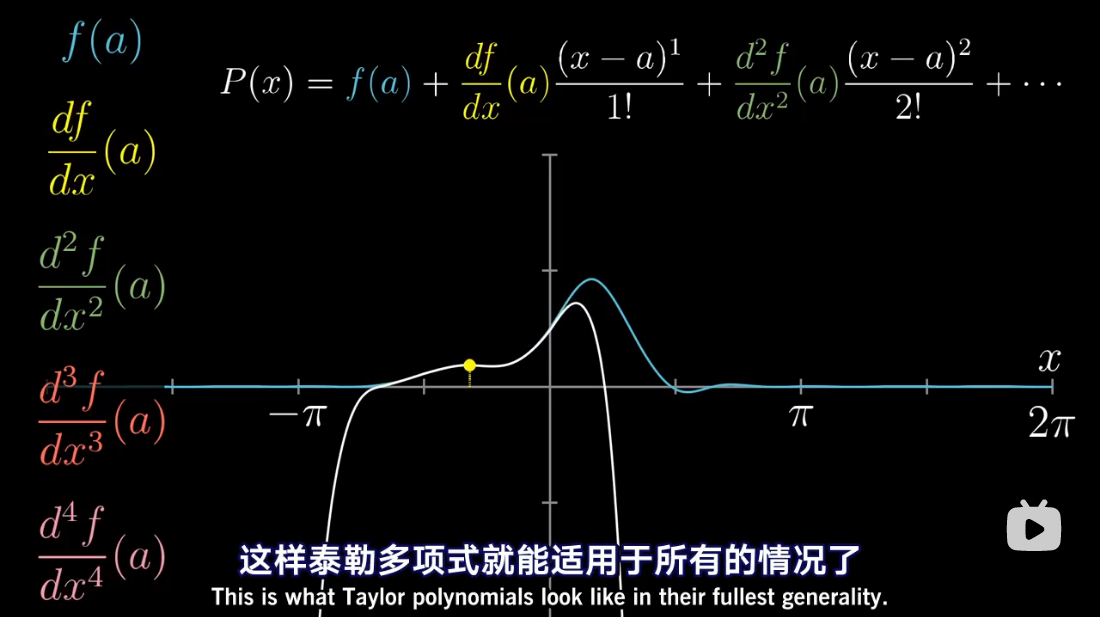
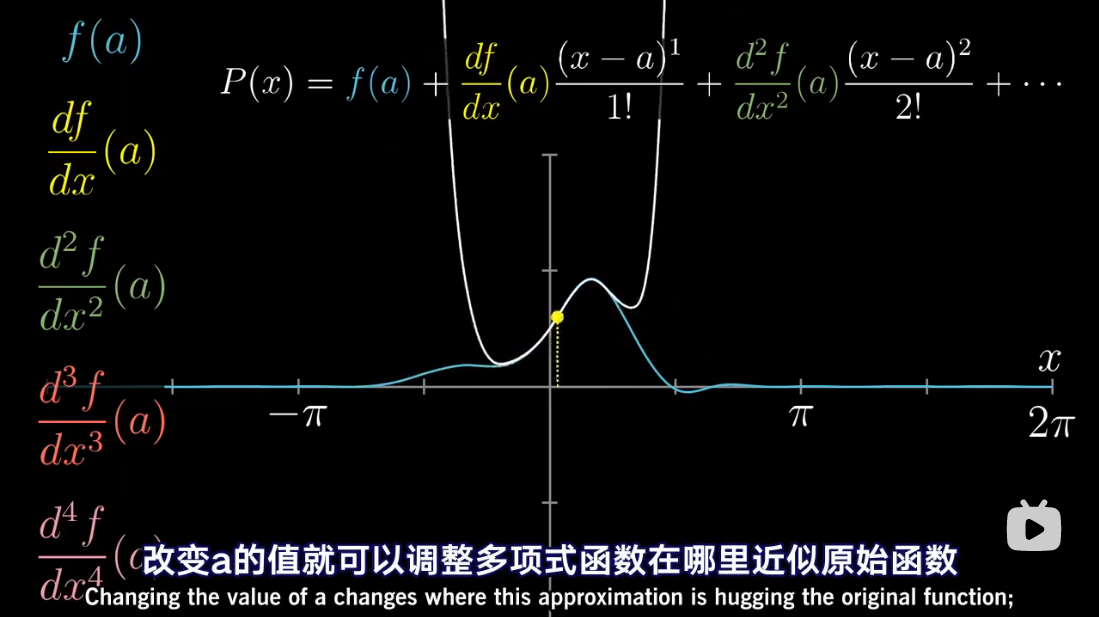
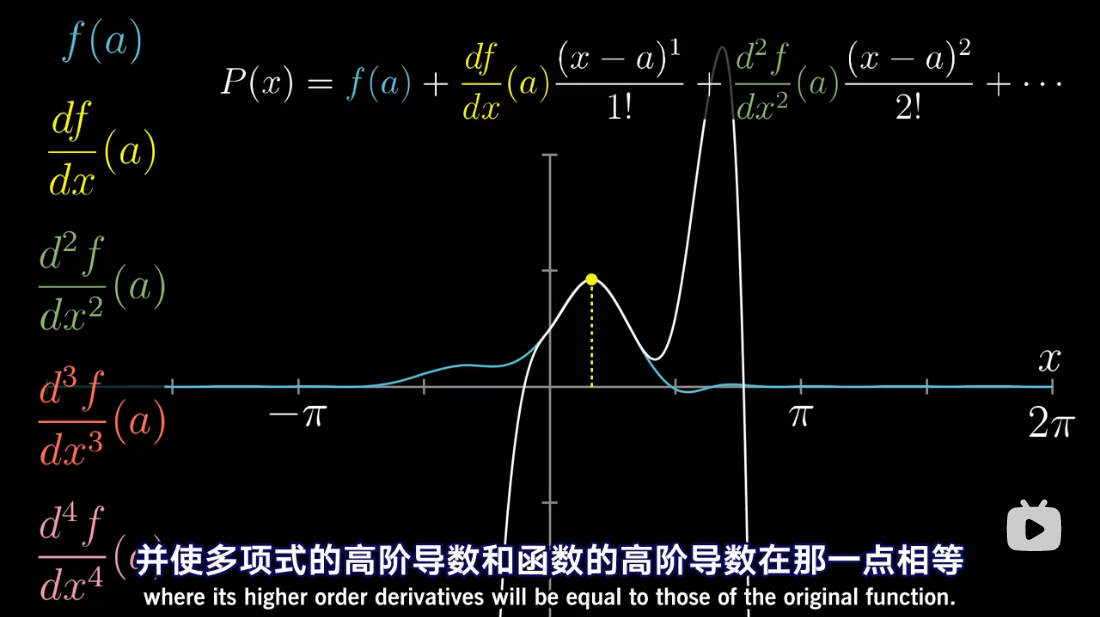
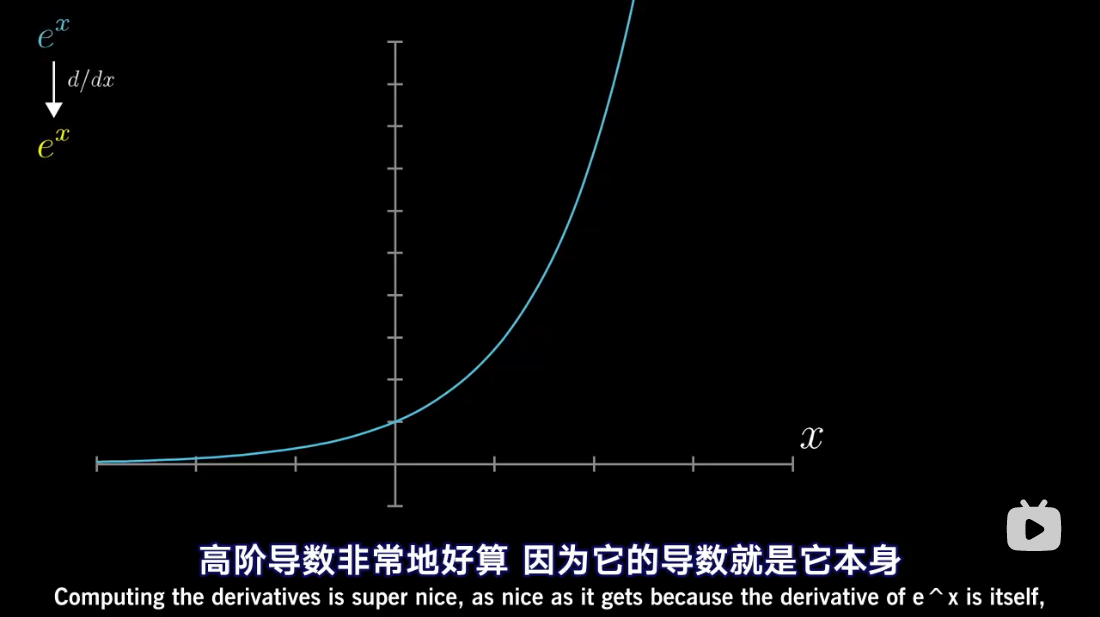
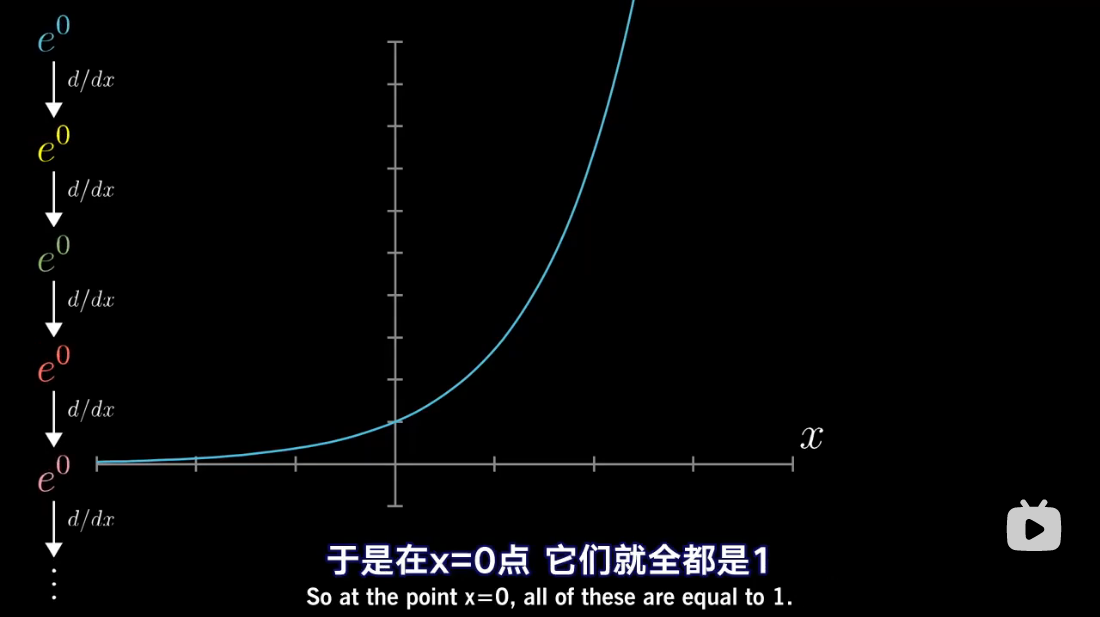
泰勒多项式几何解释

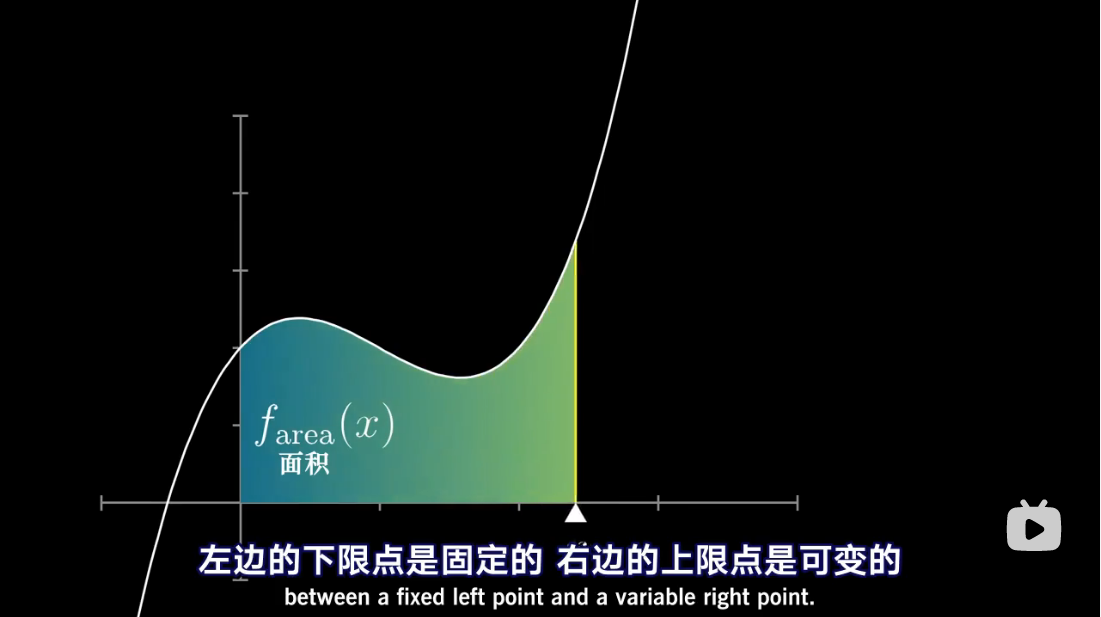
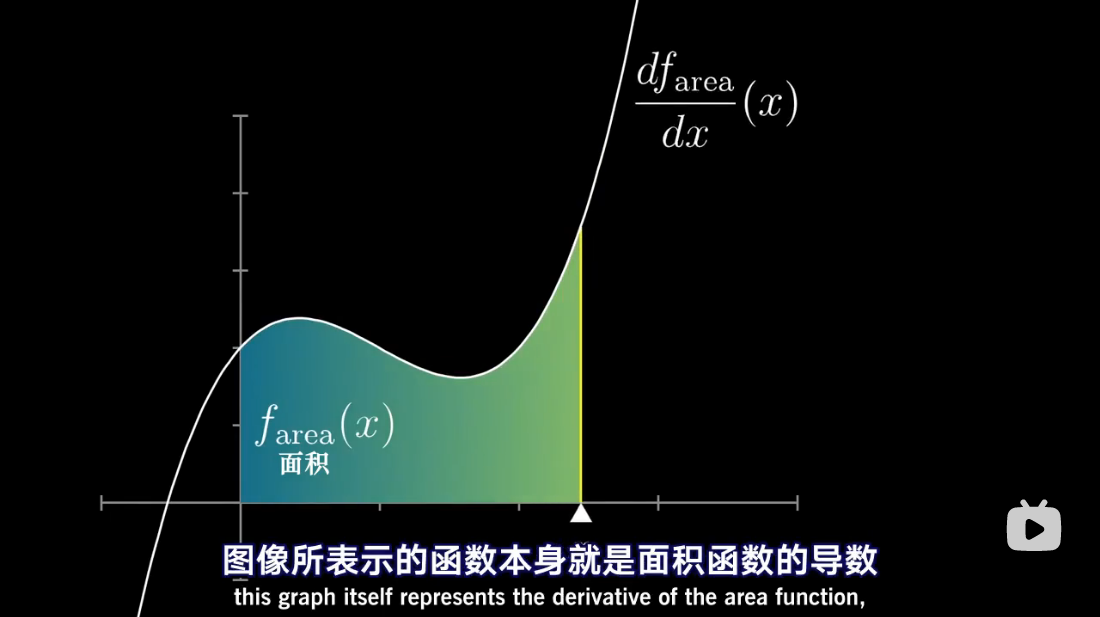
泰勒对应项

级数

泰勒多项式

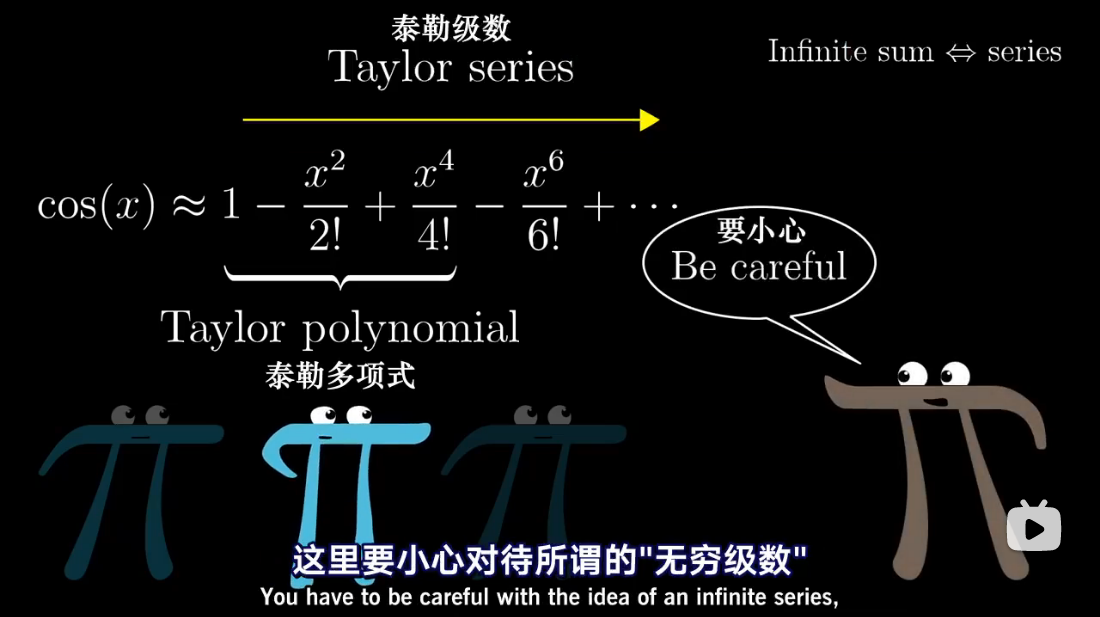
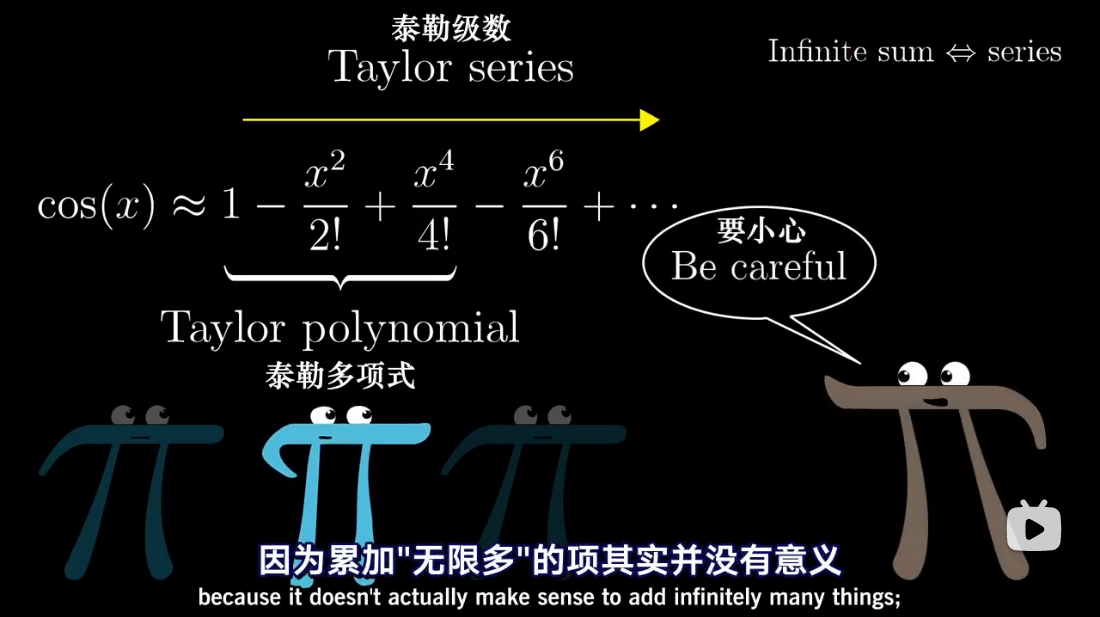
收敛

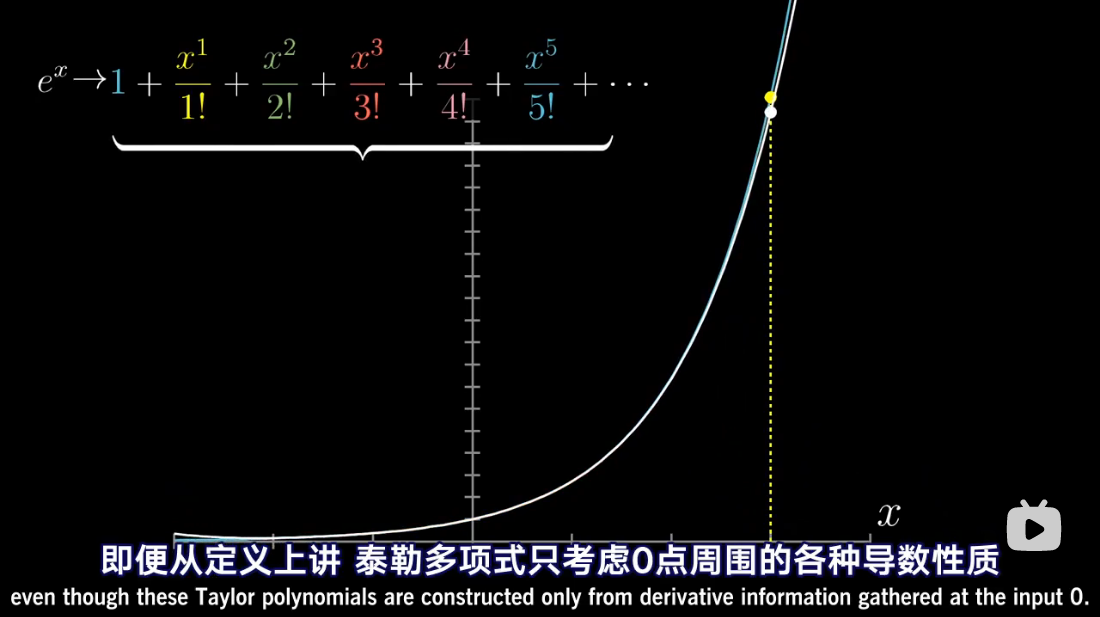
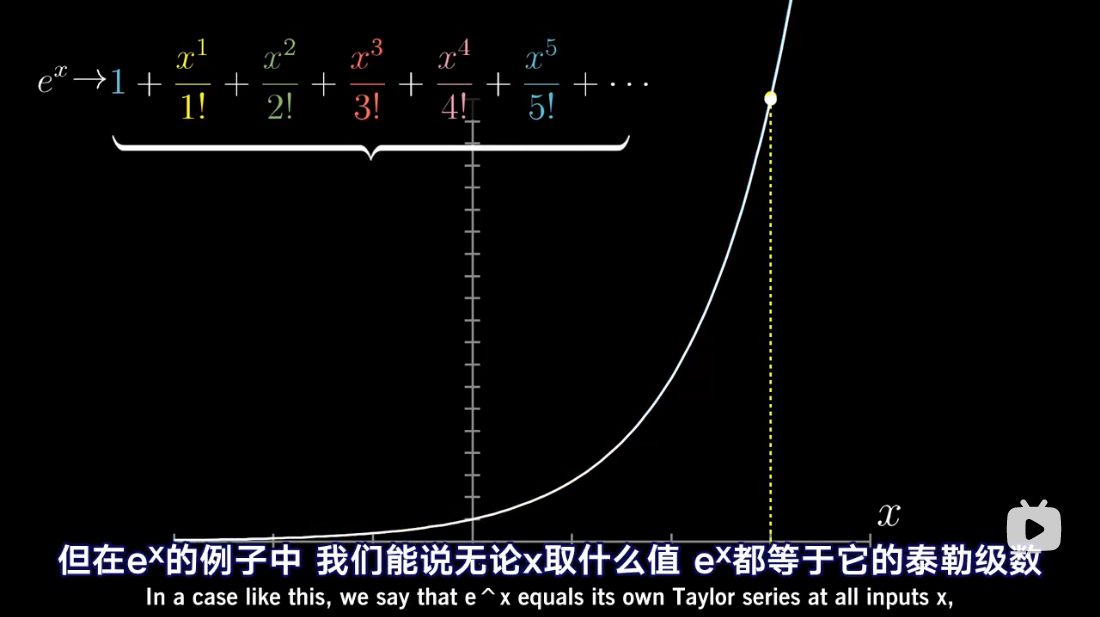
发散

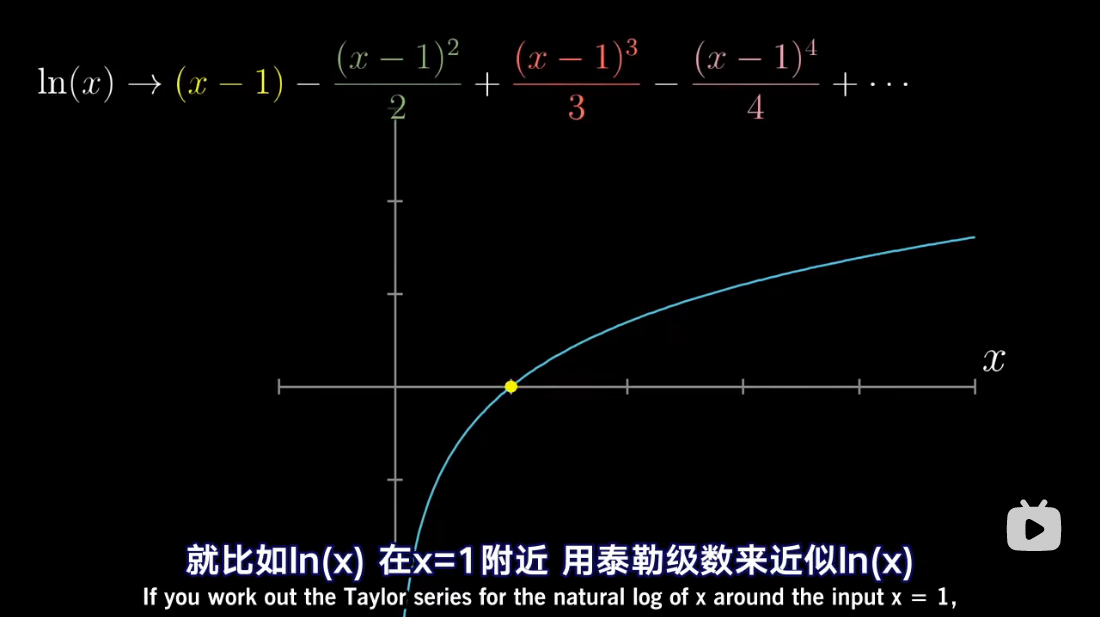
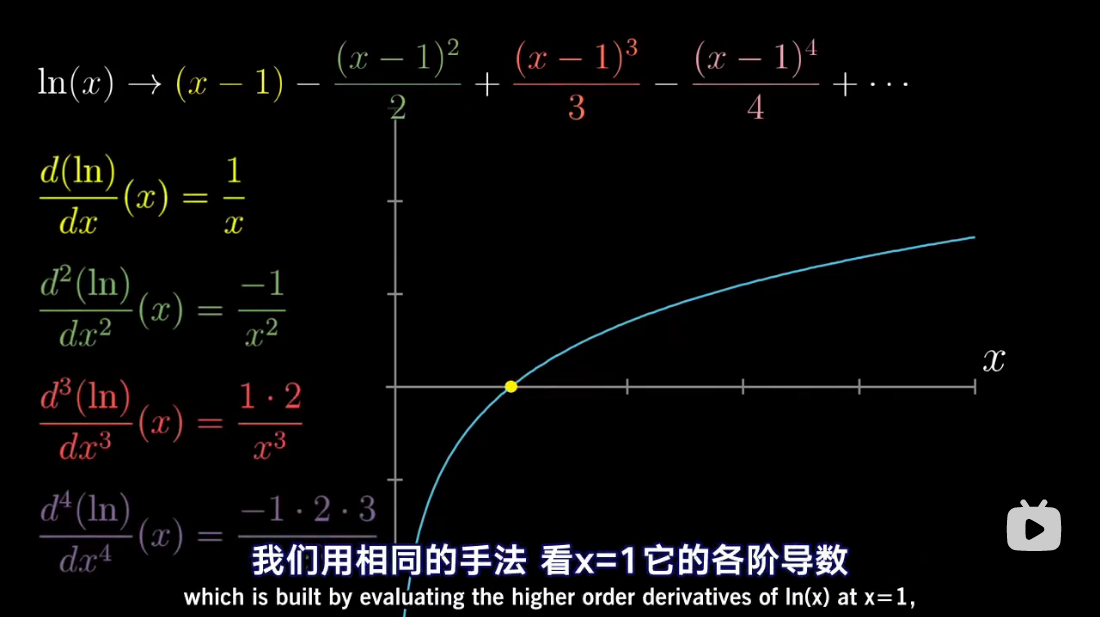
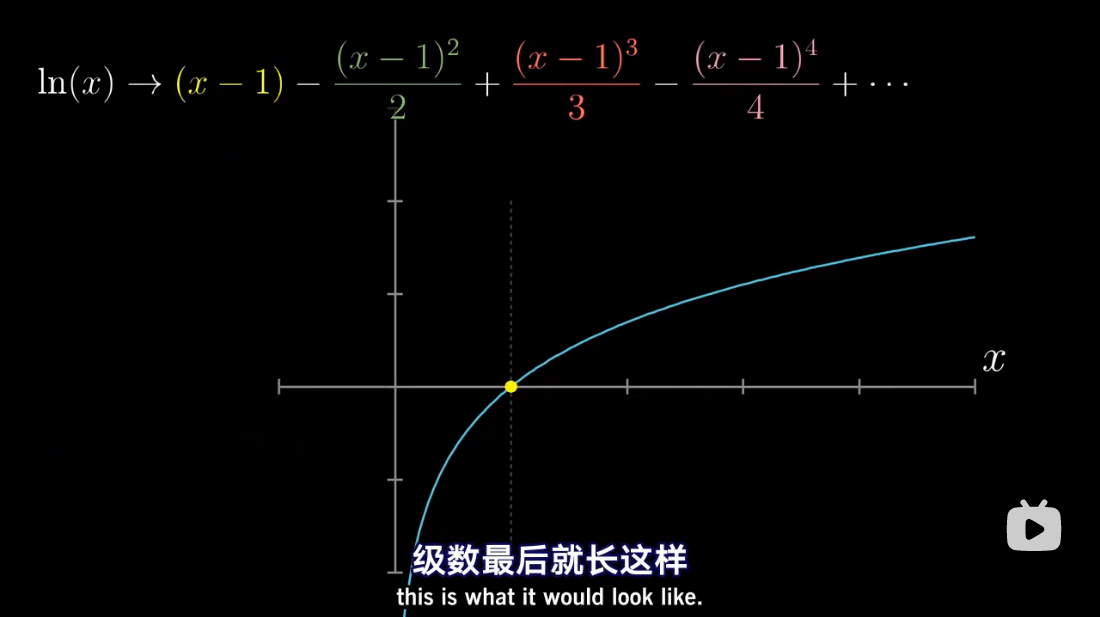
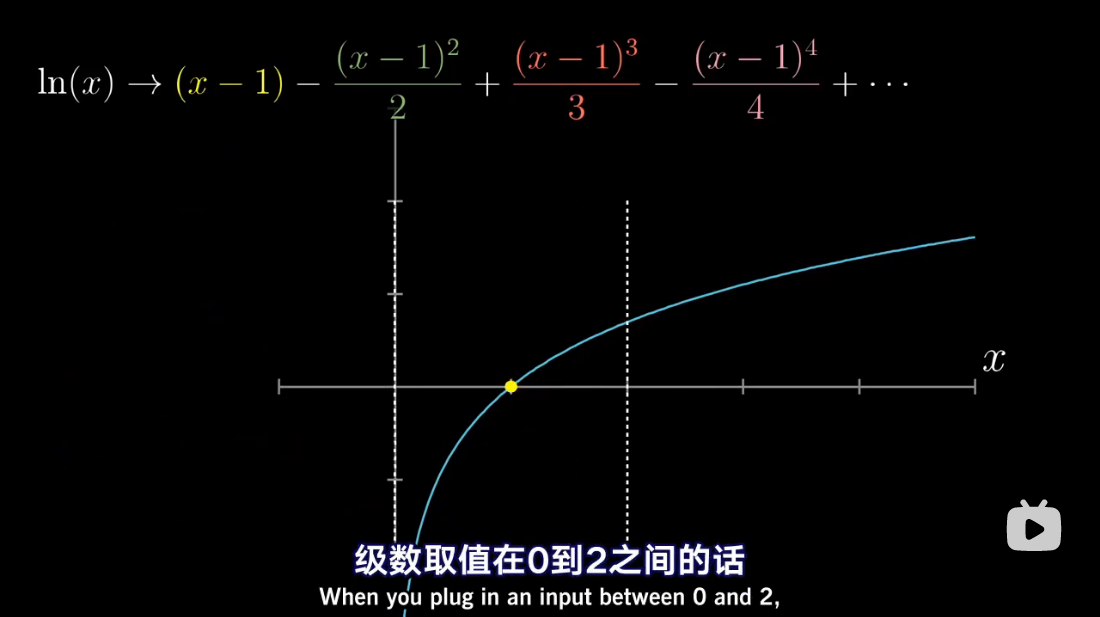
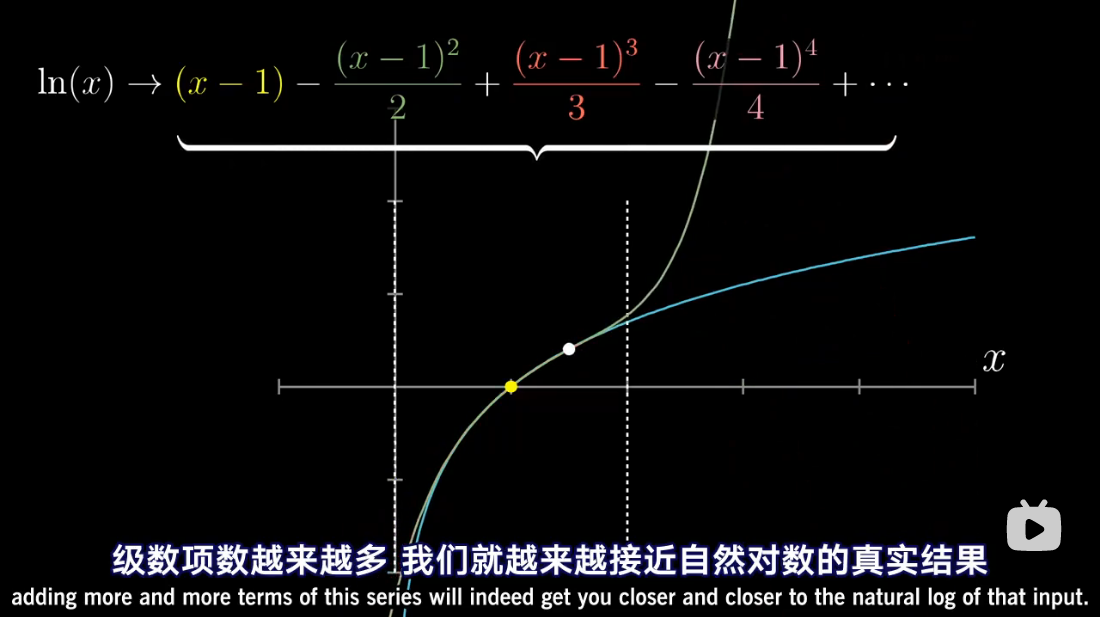
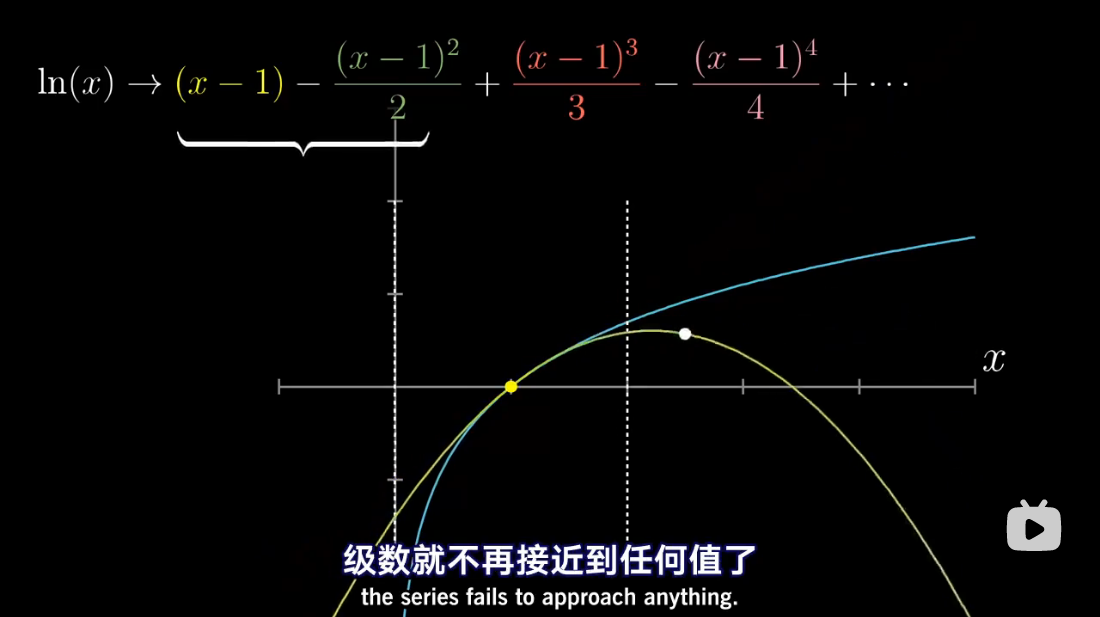
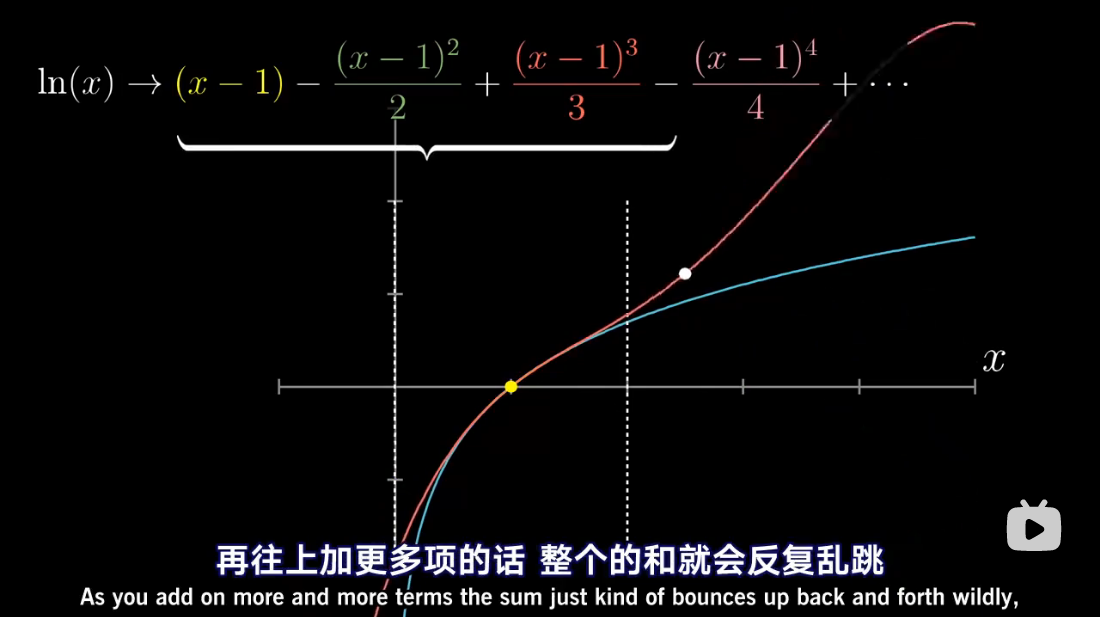
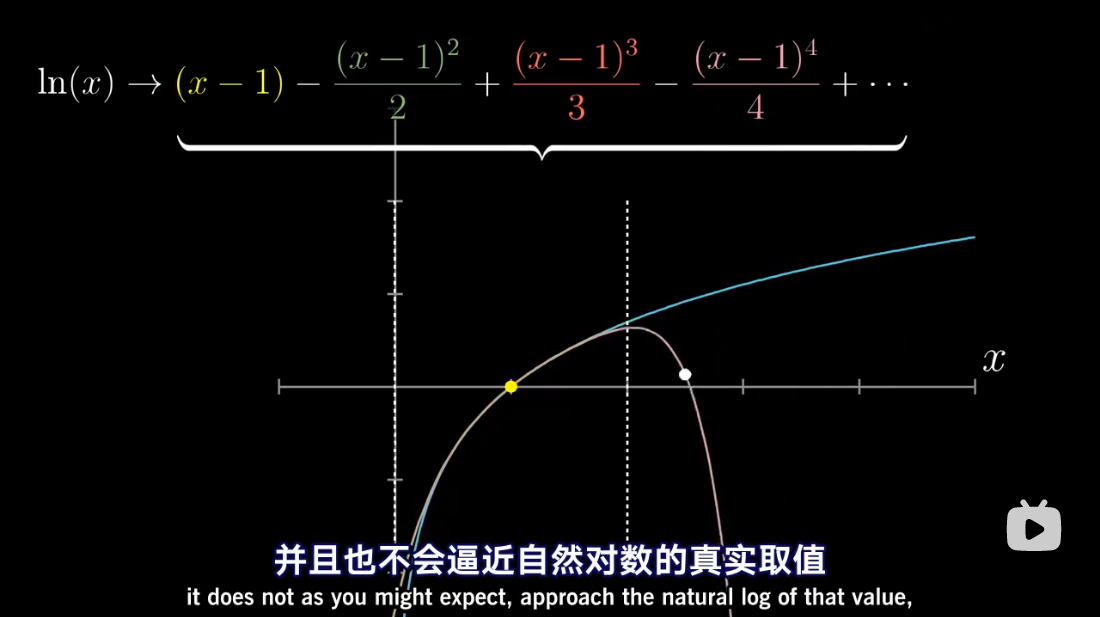
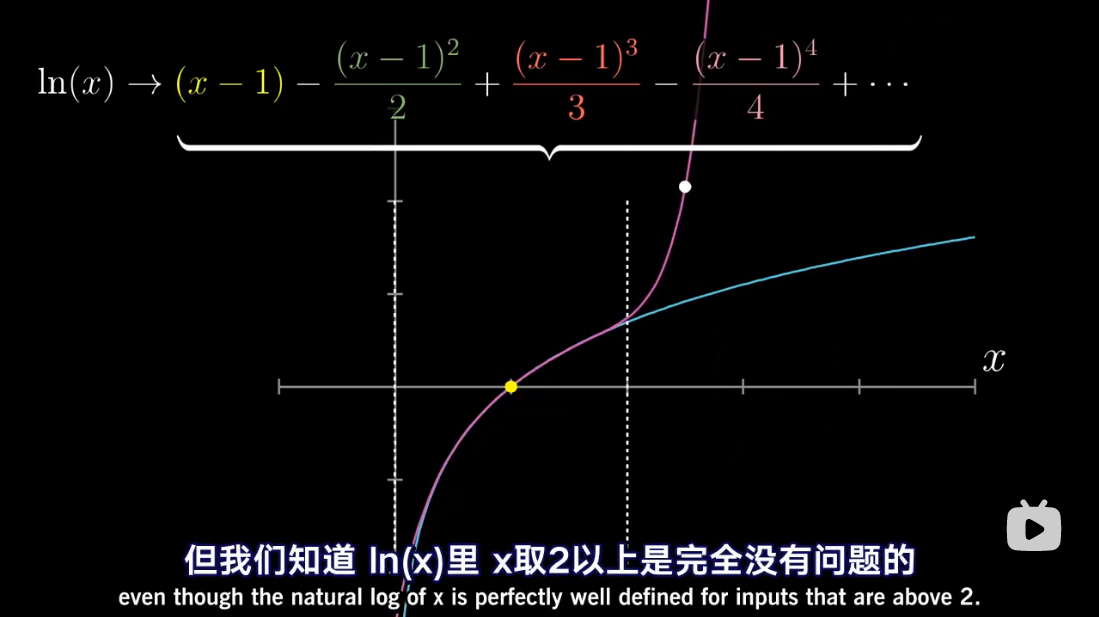
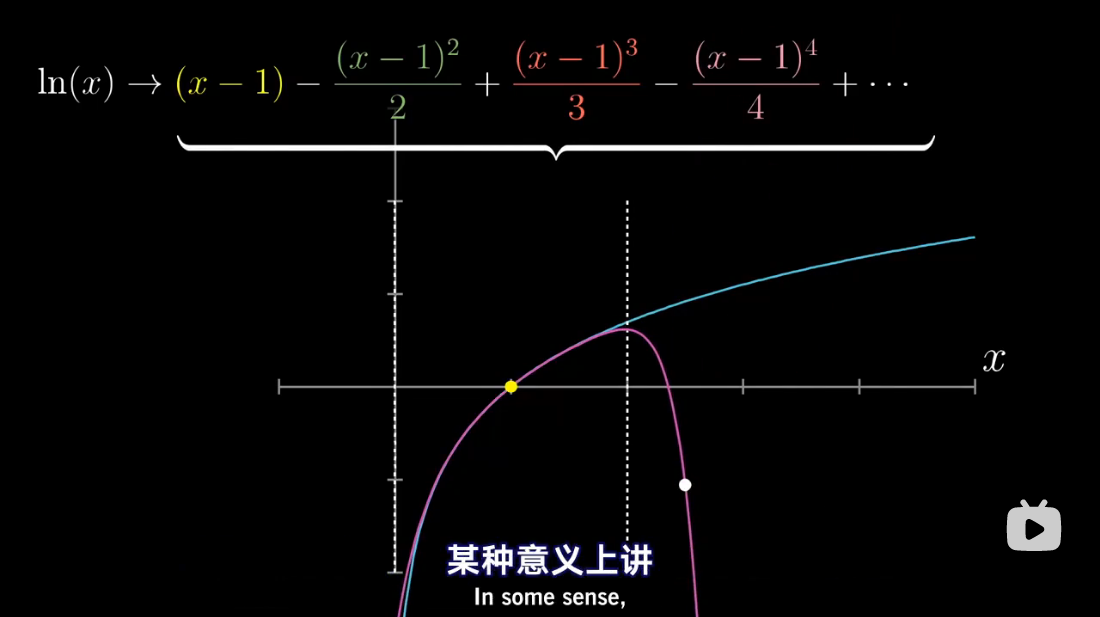
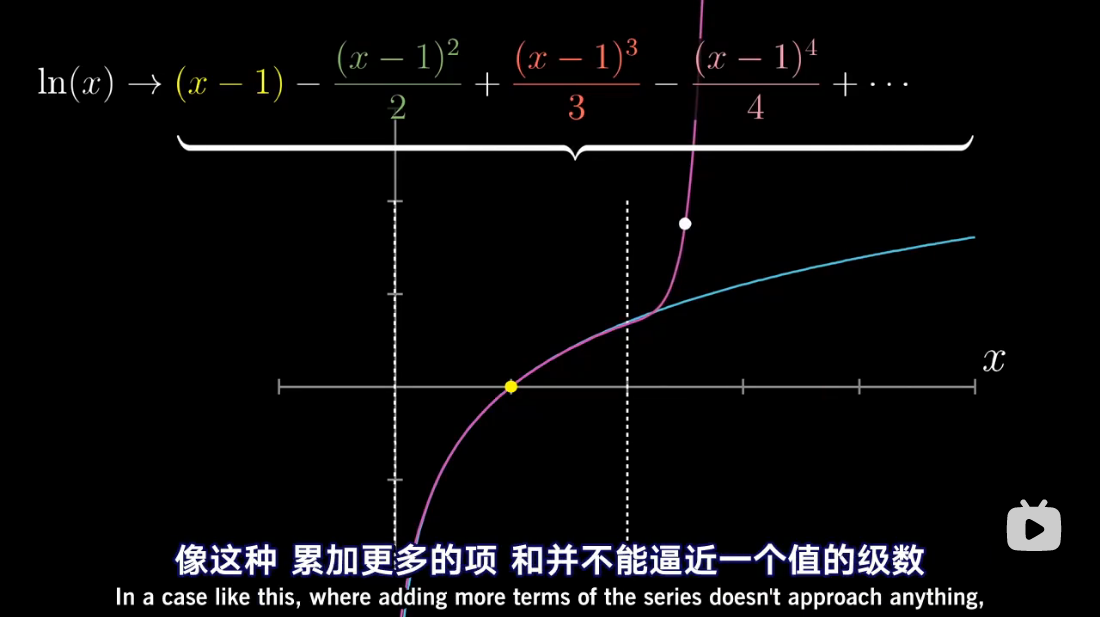
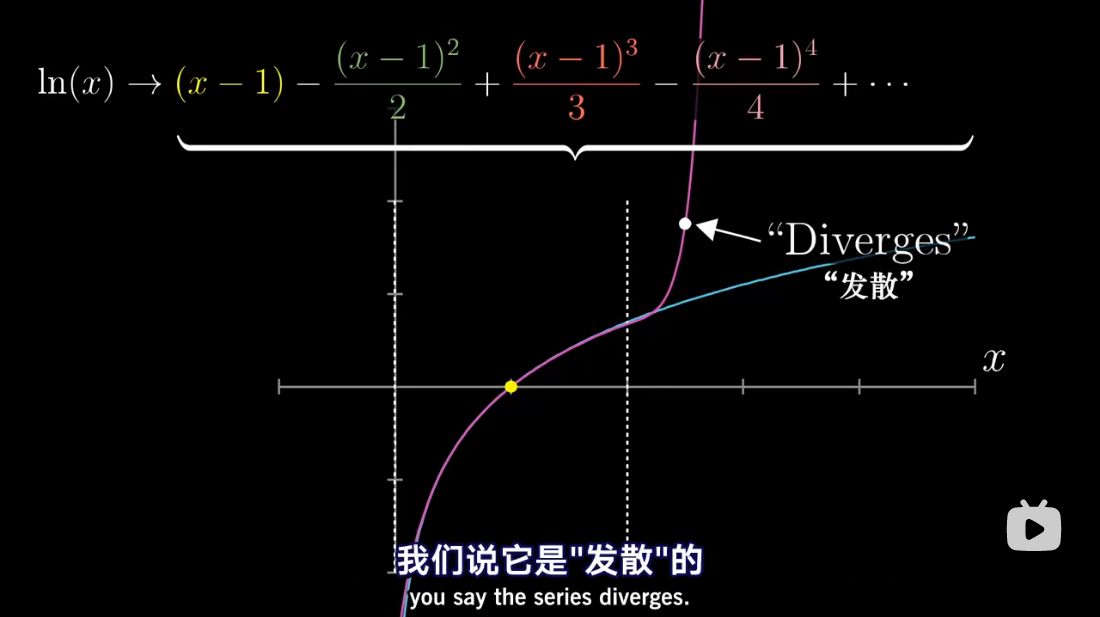
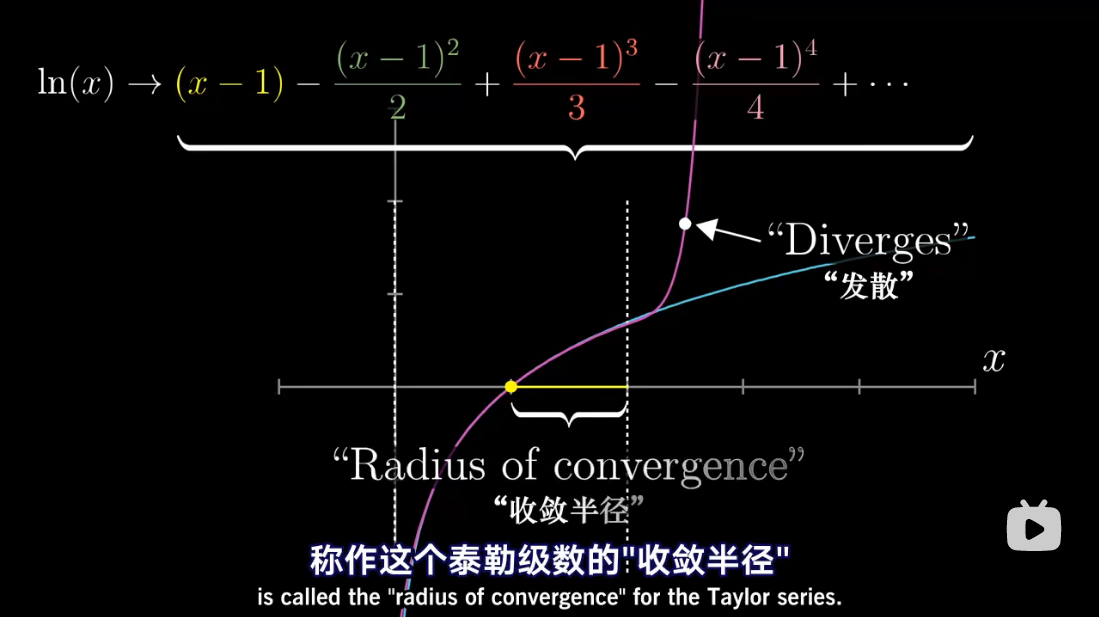
泰勒级数是利用函数某单个点的导数，来近似该点附近函数的值。

---

via:

• 泰勒公式（泰勒展开式）通俗+本质详解-优快云博客
  https://blog.youkuaiyun.com/qq_38646027/article/details/88014692

• 泰勒公式（泰勒展开式）通俗+本质详解-优快云博客
  https://blog.youkuaiyun.com/qq_38646027/article/details/88014692

• 数学基础 – 泰勒展开式-优快云博客
  https://blog.youkuaiyun.com/sz66cm/article/details/140621607

• 常见函数的泰勒级数展开_指数函数泰勒展开-优快云博客
  https://blog.youkuaiyun.com/flyfish1986/article/details/140415901

• 常见函数泰勒公式展开（清晰）-优快云博客
  https://blog.youkuaiyun.com/Infinity_07/article/details/113830088

  • tan(x)的泰勒展开有通项公式吗？ - 知乎
    https://www.zhihu.com/question/304948467
  • 微积分 | 常用等价无穷小的整理 | 清晰_等价无穷小公式大全-优快云博客
    https://blog.youkuaiyun.com/Infinity_07/article/details/121469317

• 泰勒展开式（常见）-优快云博客
  https://blog.youkuaiyun.com/weixin_49342084/article/details/142922686