注:本文为 “微积分基础” 整理。
zhihu 引文,略作重排。
如有内容异常,请看原文。
微积分入门基础
爱 XR 的麦子 编辑于 2024-03-09 16:28・上海 2025-06-17 20:02 更新
前言
微分的表示方法有多种。例如, f ′ f' f′ 是一种常见的表示方式,但它容易让人忽略是对哪个变量进行微分。因此,更推荐使用 d f d x \frac{df}{dx} dxdf 或 d d x ( f ( x ) ) \frac{d}{dx}\left(f(x)\right) dxd(f(x))。在本文中, d d x \frac{d}{dx} dxd 可以被看作是一个操作符。此外,还有一种常见的表示是 f ˙ \dot{f} f˙,在物理学中通常表示对时间 t t t 的微分。
本文的重点并非提供一套严谨的数学推导。主流的微积分推导基于 ε − δ \varepsilon - \delta ε−δ 体系。如果读者对这一套不适应,可以尝试了解无限小量的相关内容。
一次函数
一次函数 (Linear Function)
设函数 f ( x ) = y = k x + b f(x) = y = kx + b f(x)=y=kx+b。若理解微分是求斜率,则答案显而易见,即 k k k。计算 k k k 的方法如下:
k = y 1 − y 0 x 1 − x 0 k = \frac{y_1 - y_0}{x_1 - x_0} k=x1−x0y1−y0
对于一次函数而言,该斜率对任意 x x x 均适用。因此,可以写为:
d f d x = k \frac{df}{dx} = k dxdf=k
进一步改写 k k k,令 x 1 − x 0 = h x_1 - x_0 = h x1−x0=h,则有:
d f d x ( x 0 ) = k = f ( x 0 + h ) − f ( x 0 ) x 0 + h − x 0 = f ( x 0 + h ) − f ( x 0 ) h \begin{aligned} \frac{df}{dx}(x_0) &= k \\ &= \frac{f(x_0 + h) - f(x_0)}{x_0 + h - x_0} \\ &= \frac{f(x_0 + h) - f(x_0)}{h} \end{aligned} dxdf(x0)=k=x0+h−x0f(x0+h)−f(x0)=hf(x0+h)−f(x0)
由于一次函数的斜率对任意 x x x 均适用,且 h h h 的大小无关紧要,因此可得:
d f d x = k = f ( x + h ) − f ( x ) h \frac{df}{dx} = k = \frac{f(x + h) - f(x)}{h} dxdf=k=hf(x+h)−f(x)
二次函数
二次函数 (Quadratic Function)
设函数 f ( x ) = y = a x 2 f(x) = y = a x^2 f(x)=y=ax2。
微分的目的是找到过某一点的切线,以求得该点的斜率。然而,存在两个问题:
- 过一点可作无数条直线
- 两点确定一条直线
这两个问题看似无法调和。因此,微分的核心思想是:当 h h h 不断减小时,两点不断靠近,最终这两点连成的直线的斜率即为该点的斜率,且该斜率应是唯一的。
因此,求微分时,实际上是在求:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h \frac{df}{dx} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} dxdf=h→0limhf(x+h)−f(x)
接下来,进行推导:
d f d x = lim h → 0 a ( x + h ) 2 − a x 2 h \frac{df}{dx} = \lim_{h \rightarrow 0} \frac{a(x + h)^2 - a x^2}{h} dxdf=h→0limha(x+h)2−ax2
展开完全平方公式后,得:
d f d x = lim h → 0 a x 2 + 2 a x h + a h 2 − a x 2 h = lim h → 0 2 a x h + a h 2 h = lim h → 0 2 a x + a h \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{a x^2 + 2 a x h + a h^2 - a x^2}{h} \\ &= \lim_{h \rightarrow 0} \frac{2 a x h + a h^2}{h} \\ &= \lim_{h \rightarrow 0} 2 a x + a h \end{aligned} dxdf=h→0limhax2+2axh+ah2−ax2=h→0limh2axh+ah2=h→0lim2ax+ah
显然,极限仅作用于第二项,因此最终结果为:
f ( x ) = a x 2 ⇒ d f d x = 2 a x f(x) = a x^2 \quad \Rightarrow \quad \frac{df}{dx} = 2 a x f(x)=ax2⇒dxdf=2ax
多项式函数(幂为正整数)
多项式函数 (Polynomial Function)
设函数 f ( x ) = a x n f(x) = a x^n f(x)=axn,其中 n n n 为任意正整数。
继续使用上述方法:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 a ( x + h ) n − a x n h \frac{df}{dx} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} = \lim_{h \rightarrow 0} \frac{a(x + h)^n - a x^n}{h} dxdf=h→0limhf(x+h)−f(x)=h→0limha(x+h)n−axn
接下来需要展开第一项。展开是关键步骤之一。
杨辉三角
杨辉三角的规律是:左上和右上两数之和等于下面的数。杨辉三角的值也是二项式展开的系数。
例如,第三行是完全平方公式的系数。

二项式展开
当 n n n 是具体值且较小时,使用杨辉三角较为方便。但对于任意 n n n 或较大数值时,使用公式更为合适:
( a + b ) n = ∑ k = 0 n n C k a k b n − k (a + b)^n = \sum_{k=0}^n {}^nC_k\ a^k b^{n-k} (a+b)n=k=0∑nnCk akbn−k
其中, n C k {}^nC_k nCk 的含义如下:
n C k = n ! ( n − k ) ! k ! {}^nC_k = \frac{n!}{(n-k)! k!} nCk=(n−k)!k!n!
阶乘、排列、组合
阶乘 (Factorial),记作 n ! n! n!,表示 n n n 个物体的排列方式数量。例如,对于 A A A、 B B B、 C C C 三个物体,共有 6 种排列方式:
- A B C ABC ABC
- A C B ACB ACB
- B A C BAC BAC
- B C A BCA BCA
- C A B CAB CAB
- C B A CBA CBA
另一种理解方式是:将三个物体依次放入三个位置。第一个位置有 3 种选择;当第一个位置确定后,第二个位置有 2 种选择;当第二个位置确定后,最后一个位置只有 1 种选择,即 3 × 2 × 1 3 \times 2 \times 1 3×2×1,这就是 3 ! 3! 3! 的含义。因此,
n ! = n × ( n − 1 ) × ( n − 2 ) × ⋯ × 2 × 1 n! = n \times (n - 1) \times (n - 2) \times \cdots \times 2 \times 1 n!=n×(n−1)×(n−2)×⋯×2×1
需要注意以下三点:
- 阶乘的定义通常以递归形式表示:
n ! = n × ( n − 1 ) ! 且 0 ! = 1 n! = n \times (n - 1)! \quad \text{且} \quad 0! = 1 n!=n×(n−1)!且0!=1
-
0 ! = 1 0! = 1 0!=1 是直观的。如果 n ! n! n! 表示 n n n 个物体的排列方式数量,那么 0 ! 0! 0! 表示 0 个物体的排列方式数量,答案是 1 种,即“空白”。
-
阶乘通常用于正整数和 0。如果需要讨论任意实数,则需要引入伽马函数(Gamma Function),此处不展开讨论。
排列 (Permutation),记作 n P r {}^nP_r nPr,表示从 n n n 个物体中选取 r r r 个进行排列的方式数量。例如,从 A A A、 B B B、 C C C 中选取 1 个进行排列,有 3 种方式:
- A A A
- B B B
- C C C
如果选取 2 个进行排列,则有 6 种方式:
- A B AB AB
- A C AC AC
- B A BA BA
- B C BC BC
- C A CA CA
- C B CB CB
排列的公式为:
n P r = n ! ( n − r ) ! {}^nP_r = \frac{n!}{(n - r)!} nPr=(n−r)!n!
其含义是:对 n n n 个物体进行排列,但对 ( n − r ) (n - r) (n−r) 个物体的排列“不在意”,因此将其除掉。
组合 (Combination),记作 n C r {}^nC_r nCr,表示从 n n n 个物体中选取 r r r 个的方式数量。其公式为:
n C r = n ! ( n − r ) ! r ! = n P r r ! {}^nC_r = \frac{n!}{(n - r)! r!} = \frac{{}^nP_r}{r!} nCr=(n−r)!r!n!=r!nPr
组合的含义是:对 n n n 个物体进行排列,但对 ( n − r ) (n - r) (n−r) 个物体的排列“不在意”,同时对选取的 r r r 个物体的排列也“不在意”。换言之,放入坑中的物体的排列顺序无关紧要。这就是组合的定义。
更常见的解释是:组合表示“挑选”的方式数量。例如,从 A A A、 B B B、 C C C 三个物体中挑选 2 个,有 3 种方式:
- A B AB AB
- A C AC AC
- B C BC BC
计算过程如下:
3 C 2 = 3 P 2 2 ! = 3 ! ( 3 − 2 ) ! 2 ! = 3 × 2 × 1 1 × 2 × 1 = 3 {}^3C_2 = \frac{{}^3P_2}{2!} = \frac{3!}{(3 - 2)! 2!} = \frac{3 \times 2 \times 1}{1 \times 2 \times 1} = 3 3C2=2!3P2=(3−2)!2!3!=1×2×13×2×1=3
组合公式通常写为:
n C k = n ! ( n − r ) ! r ! = n × ( n − 1 ) × ⋯ × ( n − r + 1 ) r ! {}^nC_k = \frac{n!}{(n - r)! r!} = \frac{n \times (n - 1) \times \cdots \times (n - r + 1)}{r!} nCk=(n−r)!r!n!=r!n×(n−1)×⋯×(n−r+1)
回到多项式函数的讨论:
( x + h ) n = x n + n x n − 1 h + n ( n − 1 ) 2 x n − 2 h 2 + ⋯ (x + h)^n = x^n + n x^{n - 1} h + \frac{n(n - 1)}{2} x^{n - 2} h^2 + \cdots (x+h)n=xn+nxn−1h+2n(n−1)xn−2h2+⋯
因此,
d f d x = lim h → 0 a ( x n + n x n − 1 h + n ( n − 1 ) 2 x n − 2 h 2 + ⋯ ) − a x n h = lim h → 0 a x n + a n x n − 1 h + a n ( n − 1 ) 2 x n − 2 h 2 + ⋯ − a x n h = lim h → 0 a n x n − 1 + a n ( n − 1 ) 2 x n − 2 h + ⋯ \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{a(x^n + n x^{n - 1} h + \frac{n(n - 1)}{2} x^{n - 2} h^2 + \cdots) - a x^n}{h}\\ &= \lim_{h \rightarrow 0} \frac{a x^n + a n x^{n - 1} h + a \frac{n(n - 1)}{2} x^{n - 2} h^2 + \cdots - a x^n}{h}\\ &= \lim_{h \rightarrow 0} a n x^{n - 1} + a \frac{n(n - 1)}{2} x^{n - 2} h + \cdots \end{aligned} dxdf=h→0limha(xn+nxn−1h+2n(n−1)xn−2h2+⋯)−axn=h→0limhaxn+anxn−1h+a2n(n−1)xn−2h2+⋯−axn=h→0limanxn−1+a2n(n−1)xn−2h+⋯
由于极限仅作用于第一项,因此最终结果为:
f ( x ) = a x n ⇒ d f d x = a n x n − 1 f(x) = a x^n \quad \Rightarrow \quad \frac{df}{dx} = a n x^{n - 1} f(x)=axn⇒dxdf=anxn−1
多项式函数(幂为负整数)
许多学生直接使用上述公式,部分学生知道推导过程,但当被问及“当 n n n 为负数或分数时,该公式是否仍然适用?”时,他们往往会感到困惑。虽然大家都知道公式仍然适用,但上述推导是否要求 n > 0 n > 0 n>0 呢?
因此,当 n n n 为负数或分数时,需要分别进行推导。
设函数 f ( x ) = a x − n f(x) = a x^{-n} f(x)=ax−n,其中 n n n 为正整数,公式中添加负号以保持美观。按照惯例,有:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 a ( x + h ) − n − a x − n h \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{a(x + h)^{-n} - a x^{-n}}{h} \end{aligned} dxdf=h→0limhf(x+h)−f(x)=h→0limha(x+h)−n−ax−n
在展开时遇到问题。此时需要引入牛顿的广义二项式定理(Binomial Theorem)。
广义二项式定理
为了简化表达,在讨论负数幂或分数幂的展开时,通常将数值较大的项提取出来。
( x + h ) − n = x − n ( 1 + h x ) − n (x + h)^{-n} = x^{-n} \left(1 + \frac{h}{x}\right)^{-n} (x+h)−n=x−n(1+xh)−n
因此,关注的是 ( 1 + h x ) − n \left(1 + \frac{h}{x}\right)^{-n} (1+xh)−n 这一部分。
当幂为正整数时,展开式为:
( 1 + r ) n = 1 + n r + n ( n − 1 ) 2 r 2 + ⋯ + n ( n − 1 ) 2 r n − 2 + n r n − 1 + r n (1 + r)^n = 1 + n r + \frac{n(n - 1)}{2} r^2 + \cdots + \frac{n(n - 1)}{2} r^{n - 2} + n r^{n - 1} + r^n (1+r)n=1+nr+2n(n−1)r2+⋯+2n(n−1)rn−2+nrn−1+rn
这是一个有限的展开式,且应用组合公式是合理的。
然而,当幂为负数时,为何仍可如此展开呢?在理清数理逻辑之前,牛顿并未过多纠结,而是直接使用了该方法。
( 1 + r ) − n = 1 + ( − n ) r + − n ( − n − 1 ) 2 r 2 + − n ( − n − 1 ) ( − n − 2 ) 3 ! r 3 + ⋯ (1 + r)^{-n} = 1 + (-n) r + \frac{-n(-n - 1)}{2} r^2 + \frac{-n(-n - 1)(-n - 2)}{3!} r^3 + \cdots (1+r)−n=1+(−n)r+2−n(−n−1)r2+3!−n(−n−1)(−n−2)r3+⋯
例如,当 − n = − 1 -n = -1 −n=−1 时:
( 1 + r ) − 1 = 1 − r + r 2 − r 3 + ⋯ (1 + r)^{-1} = 1 - r + r^2 - r^3 + \cdots (1+r)−1=1−r+r2−r3+⋯
可以看出,这是一个无限级数,包含无限项。但这是否合理呢?牛顿表示“似乎可以”。
( 1 + r ) × ( 1 + r ) − 1 = ( 1 + r ) ( 1 + r ) = 1 (1 + r) \times (1 + r)^{-1} = \frac{(1 + r)}{(1 + r)} = 1 (1+r)×(1+r)−1=(1+r)(1+r)=1
对于展开式进行乘法运算时,需要注意处理无限项的情况,确保项的对应关系正确:
( 1 + r ) × ( 1 − r + r 2 − r 3 + ⋯ ) = 1 × ( 1 − r + r 2 − r 3 + ⋯ ) + r × ( 1 − r + r 2 − r 3 + ⋯ ) = ( 1 − r + r 2 − r 3 + ⋯ ) + ( r − r 2 + r 3 − ⋯ ) = 1 \begin{aligned} (1 + r) \times (1 - r + r^2 - r^3 + \cdots) &= 1 \times (1 - r + r^2 - r^3 + \cdots) + r \times (1 - r + r^2 - r^3 + \cdots)\\ &= (1 - r + r^2 - r^3 + \cdots) + (r - r^2 + r^3 - \cdots) \\ &= 1 \end{aligned} (1+r)×(1−r+r2−r3+⋯)=1×(1−r+r2−r3+⋯)+r×(1−r+r2−r3+⋯)=(1−r+r2−r3+⋯)+(r−r2+r3−⋯)=1
从第二项开始,各项相互抵消,最终只剩下 1。如果对消项过程感到困惑(“不应该差一项吗?”),可以借此机会深入理解“无限”的概念。牛顿认为, ( 1 + r ) − 1 (1 + r)^{-1} (1+r)−1 与 ( 1 + r ) (1 + r) (1+r) 相乘得到 1,二者互为逆元,而无限项也具有这一性质,因此可以认为该无限级数与 ( 1 + r ) − 1 (1 + r)^{-1} (1+r)−1 等效。
回到问题:
d f d x = lim h → 0 a ( x + h ) − n − a x − n h = lim h → 0 a x − n ( 1 + h x ) − n − a x − n h = lim h → 0 a x − n ( 1 − n h x + n ( n + 1 ) 2 ( h x ) 2 − ⋯ ) − a x − n h = lim h → 0 − n a x − n h x + n ( n + 1 ) 2 a x − n ( h x ) 2 − ⋯ h = lim h → 0 − n a x − n − 1 + n ( n + 1 ) 2 a x − n − 2 h − ⋯ \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{a(x + h)^{-n} - a x^{-n}}{h} \\ &= \lim_{h \rightarrow 0} \frac{a x^{-n} \left(1 + \frac{h}{x}\right)^{-n} - a x^{-n}}{h}\\ &= \lim_{h \rightarrow 0} \frac{a x^{-n} \left(1 - n \frac{h}{x} + \frac{n(n + 1)}{2} \left(\frac{h}{x}\right)^2 - \cdots \right) - a x^{-n}}{h}\\ &= \lim_{h \rightarrow 0} \frac{-n a x^{-n} \frac{h}{x} + \frac{n(n + 1)}{2} a x^{-n} \left(\frac{h}{x}\right)^2 - \cdots}{h}\\ &= \lim_{h \rightarrow 0} -n a x^{-n - 1} + \frac{n(n + 1)}{2} a x^{-n - 2} h - \cdots\\ \end{aligned} dxdf=h→0limha(x+h)−n−ax−n=h→0limhax−n(1+xh)−n−ax−n=h→0limhax−n(1−nxh+2n(n+1)(xh)2−⋯)−ax−n=h→0limh−nax−nxh+2n(n+1)ax−n(xh)2−⋯=h→0lim−nax−n−1+2n(n+1)ax−n−2h−⋯
第一项不受极限影响,因此最终结果为:
f ( x ) = a x − n ⇒ d f d x = − n a x − n − 1 f(x) = a x^{-n} \quad \Rightarrow \quad \frac{df}{dx} = -n a x^{-n - 1} f(x)=ax−n⇒dxdf=−nax−n−1
多项式函数(幂为分数)
设函数 f ( x ) = a x 1 n f(x) = a x^{\frac{1}{n}} f(x)=axn1。
可以使用牛顿的广义二项式定理。此处采用另一种方法进行推导,同时引入微分中两个重要的方法。
链式法则
链式法则 (Chain Rule) 是微积分中极为重要的法则之一(另一个将在下文提到;此处虽仅讨论微分,但换元积分法本质上是链式法则的逆运算)。用一种可能令数学系读者不满的写法表示为:
d f d x = d f d m d m d n d n d p d p d q d q d x \frac{df}{dx} = \frac{df}{dm} \frac{dm}{dn} \frac{dn}{dp} \frac{dp}{dq} \frac{dq}{dx} dxdf=dmdfdndmdpdndqdpdxdq
中间的项如同链条一般,将 d f df df 与 d x dx dx 连接起来。
例如,对于函数 f ( x ) = ( x 2 + 6 x ) − 3 f(x) = (x^2 + 6x)^{-3} f(x)=(x2+6x)−3,进行微分时,与其展开,不如使用链式法则,轻松解决问题。
令 u = x 2 + 6 x u = x^2 + 6x u=x2+6x,则:
d u d x = 2 x + 6 \frac{du}{dx} = 2x + 6 dxdu=2x+6
f ( u ) = u − 3 ⇒ d f d u = − 3 u − 4 f(u) = u^{-3} \quad \Rightarrow \quad \frac{df}{du} = -3 u^{-4} f(u)=u−3⇒dudf=−3u−4
d f d x = d f d u d u d x = − 3 u − 4 ( 2 x + 6 ) \frac{df}{dx} = \frac{df}{du} \frac{du}{dx} = -3 u^{-4} (2x + 6) dxdf=dudfdxdu=−3u−4(2x+6)
最终,需要得到关于 x x x 的表达式:
d f d x = − 3 ( 2 x + 6 ) ( x 2 + 6 x ) − 4 \frac{df}{dx} = -3 (2x + 6) (x^2 + 6x)^{-4} dxdf=−3(2x+6)(x2+6x)−4
链式法则在处理复杂微分问题时极为重要,熟练掌握后,许多思考过程可以在脑内完成,并“跳过”某些步骤。
隐函数微分
隐函数微分 (Implicit Differentiation) 在许多场合中具有重要作用,且具有深刻的含义。这些内容可以慢慢体会,此处仅讨论一个简单的情况。
假设 y 2 = x 3 y^2 = x^3 y2=x3,求 d y d x \frac{dy}{dx} dxdy。当然,可以将 2 从 y y y 移到 x x x 的右侧,得到 y = x 3 2 y = x^{\frac{3}{2}} y=x23,然后进行微分,得到 d y d x = 3 2 x 1 2 \frac{dy}{dx} = \frac{3}{2} x^{\frac{1}{2}} dxdy=23x21。但还可以采用另一种方法:
直接对两边进行微分,但需明确是对 x x x 进行微分:
d d x ( y 2 ) = d d x ( x 3 ) \frac{d}{dx}(y^2) = \frac{d}{dx}(x^3) dxd(y2)=dxd(x3)
左侧是一个关于 y y y 的函数,即 f ( y ) = y 2 f(y) = y^2 f(y)=y2,因此不能直接对 x x x 进行微分,但可以使用链式法则:
d d y ( y 2 ) d y d x = d d x ( x 3 ) \frac{d}{dy}(y^2) \frac{dy}{dx} = \frac{d}{dx}(x^3) dyd(y2)dxdy=dxd(x3)
2 y d y d x = 3 x 2 2y \frac{dy}{dx} = 3x^2 2ydxdy=3x2
d y d x = 3 2 x 2 y \frac{dy}{dx} = \frac{3}{2} \frac{x^2}{y} dxdy=23yx2
由于 y = x 3 2 y = x^{\frac{3}{2}} y=x23,因此:
d y d x = 3 2 x 2 y = 3 2 x 2 x 3 2 = 3 2 x 2 − 3 2 = 3 2 x 1 2 \frac{dy}{dx} = \frac{3}{2} \frac{x^2}{y} = \frac{3}{2} \frac{x^2}{x^{\frac{3}{2}}} = \frac{3}{2} x^{2 - \frac{3}{2}} = \frac{3}{2} x^{\frac{1}{2}} dxdy=23yx2=23x23x2=23x2−23=23x21
此处可能觉得隐函数微分没有必要,甚至有些繁琐。但事实上,可以利用之前学过的内容来处理更复杂的情况。
回到多项式函数的讨论:
f ( x ) = a x 1 n ⇒ [ f ( x ) ] n = a n x f(x) = a x^{\frac{1}{n}} \quad \Rightarrow \quad [f(x)]^n = a^n x f(x)=axn1⇒[f(x)]n=anx
此处多用一个括号,以明确 [ f ( x ) ] n [f(x)]^n [f(x)]n 表示 f ( x ) f(x) f(x) 的值的 n n n 次方。实际上,写成 y n y^n yn 更为合适,因为 f n ( x ) f^n(x) fn(x) 在某些场合下可能被误解为进行了 n n n 次微分。
接下来进行隐函数微分:
d d x ( y n ) = d d x ( a n x ) \frac{d}{dx}(y^n) = \frac{d}{dx}(a^n x) dxd(yn)=dxd(anx)
d d y ( y n ) d y d x = a n \frac{d}{dy}(y^n) \frac{dy}{dx} = a^n dyd(yn)dxdy=an
n y n − 1 d y d x = a n n y^{n - 1} \frac{dy}{dx} = a^n nyn−1dxdy=an
d y d x = a n n y n − 1 \frac{dy}{dx} = \frac{a^n}{n y^{n - 1}} dxdy=nyn−1an
d y d x = a n n ( a x 1 n ) n − 1 \frac{dy}{dx} = \frac{a^n}{n (a x^{\frac{1}{n}})^{n - 1}} dxdy=n(axn1)n−1an
d y d x = a n x n − 1 n \frac{dy}{dx} = \frac{a}{n x^{\frac{n - 1}{n}}} dxdy=nxnn−1a
d y d x = a n x − n − 1 n \frac{dy}{dx} = \frac{a}{n} x^{-\frac{n - 1}{n}} dxdy=nax−nn−1
d y d x = a n x − 1 + 1 n \frac{dy}{dx} = \frac{a}{n} x^{-1 + \frac{1}{n}} dxdy=nax−1+n1
因此,最终结果为:
f ( x ) = a x 1 n ⇒ d f d x = a 1 n x 1 n − 1 f(x) = a x^{\frac{1}{n}} \quad \Rightarrow \quad \frac{df}{dx} = a \frac{1}{n} x^{\frac{1}{n} - 1} f(x)=axn1⇒dxdf=an1xn1−1
至此,完成了多项式函数的证明,所有多项式的情况均满足最初看到的公式,可以放心使用:
f ( x ) = a x n ⇒ d f d x = a n x n − 1 f(x) = a x^n \quad \Rightarrow \quad \frac{df}{dx} = a n x^{n - 1} f(x)=axn⇒dxdf=anxn−1
三角函数(正弦函数)
正弦函数 (Sine Function, Sinusoidal Functions)
设函数 f ( x ) = sin ( k x ) f(x) = \sin(kx) f(x)=sin(kx),其中 k k k 为任意常数。按照之前的流程,有:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 sin ( k x + k h ) − sin ( k x ) h \frac{df}{dx} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} = \lim_{h \rightarrow 0} \frac{\sin(kx + k h) - \sin(kx)}{h} dxdf=h→0limhf(x+h)−f(x)=h→0limhsin(kx+kh)−sin(kx)
同样需要展开,此时使用和角公式。
和角公式
根据下图:
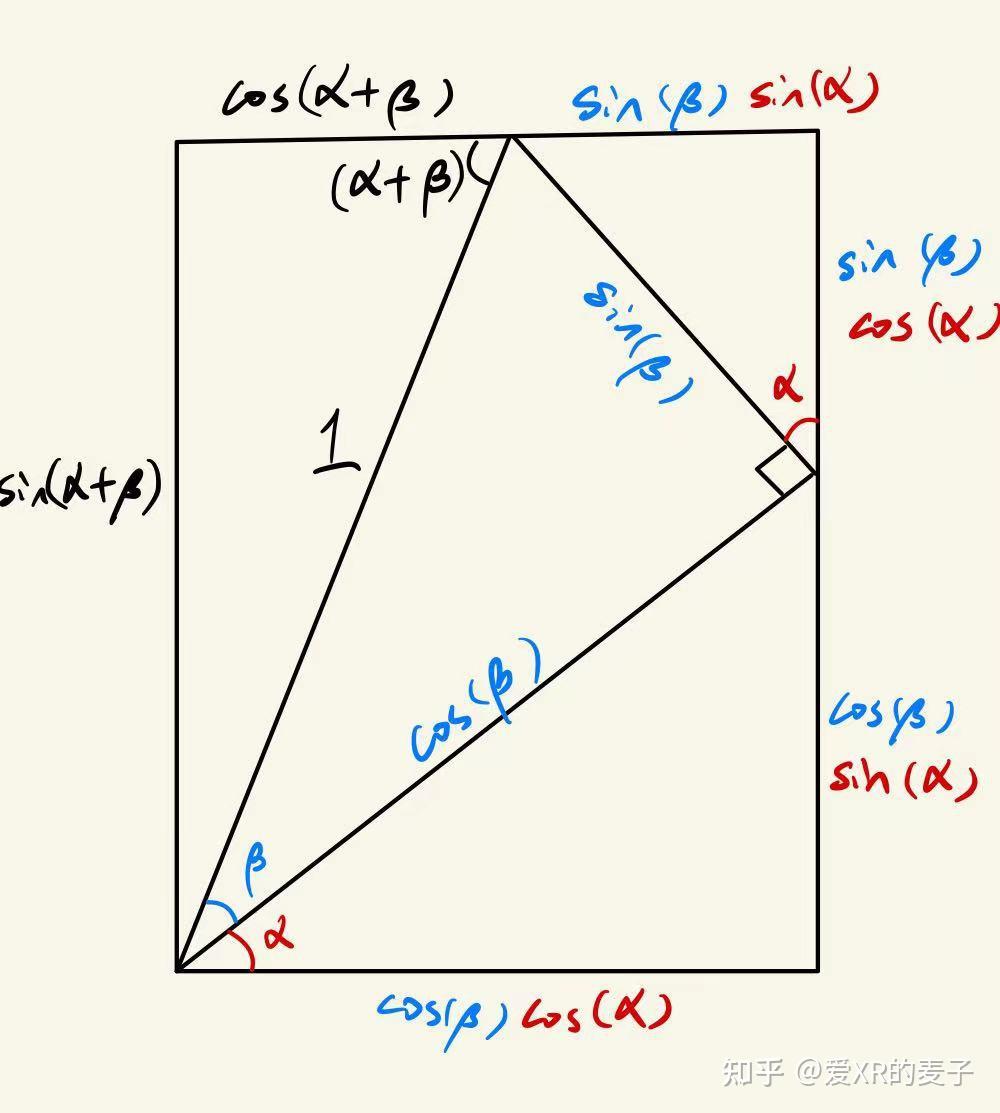
由于矩形的对边相等,因此有:
sin ( α + β ) = sin ( α ) cos ( β ) + cos ( α ) sin ( β ) \sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β ) \cos(\alpha + \beta) = \cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta) cos(α+β)=cos(α)cos(β)−sin(α)sin(β)
如果角度大于 π 2 \frac{\pi}{2} 2π,可以在圆上进行证明,但此处不展开讨论。
如果需要计算差角公式,可以使用以下公式:
sin ( − θ ) = − sin ( θ ) \sin(-\theta) = -\sin(\theta) sin(−θ)=−sin(θ)
cos ( − θ ) = cos ( θ ) \cos(-\theta) = \cos(\theta) cos(−θ)=cos(θ)
将上述公式代入即可。原则上,不建议背诵任何带有负号的公式,因为一旦搞错被减数和减数,再多的努力也将付诸东流。
回到正弦函数的讨论:
d f d x = lim h → 0 sin ( k x ) cos ( k h ) + cos ( k x ) sin ( k h ) − sin ( k x ) h = lim h → 0 ( sin ( k x ) cos ( k h ) − 1 h + cos ( k x ) sin ( k h ) h ) \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{\sin(kx) \cos(kh) + \cos(kx) \sin(kh) - \sin(kx)}{h} \\ &= \lim_{h \rightarrow 0} \left( \sin(kx) \frac{\cos(kh) - 1}{h} + \cos(kx) \frac{\sin(kh)}{h} \right) \end{aligned} dxdf=h→0limhsin(kx)cos(kh)+cos(kx)sin(kh)−sin(kx)=h→0lim(sin(kx)hcos(kh)−1+cos(kx)hsin(kh))
k x kx kx 不受 lim h → 0 \lim_{h \rightarrow 0} limh→0 的影响,因此只需考虑那两个分数的极限情况。
当 h → 0 h \rightarrow 0 h→0 时,两个分数均趋近于 0 0 \frac{0}{0} 00,因此一个常见的错误是使用洛必达法则 (L’Hôpital’s Rule)。如果 lim x → c f ( x ) g ( x ) → 0 0 \lim_{x \rightarrow c} \frac{f(x)}{g(x)} \rightarrow \frac{0}{0} limx→cg(x)f(x)→00 或 ∞ ∞ \frac{\infty}{\infty} ∞∞,则有:
lim x → c f ( x ) g ( x ) = lim x → c f ′ ( x ) g ′ ( x ) \lim_{x \rightarrow c} \frac{f(x)}{g(x)} = \lim_{x \rightarrow c} \frac{f'(x)}{g'(x)} x→climg(x)f(x)=x→climg′(x)f′(x)
洛必达法则非常实用,但它要求已知相关函数的微分。此处正在证明 sin \sin sin 的微分,因此不能使用洛必达法则。
因此,需要使用另外两个工具:单位圆 (Unit Circle) 和 夹逼定理 (Squeeze Theorem)。
单位圆
单位圆的核心在于将抽象的三角函数具体化。回想一下正弦、余弦和正切的定义,它们实际上是直角三角形三边之间的比例关系,而比例是一个较为抽象的概念。相反,单位圆是一个半径为 1 的圆,通过以下思考方式,可以轻松地将复杂的比例关系简化为线段长度与角度之间的变换关系。需要注意的是,单位圆默认角度是逆时针旋转,且角度单位为弧度。
正弦是对边与斜边的比值,而此时斜边为 1,因此正弦变为对边的实际长度:
sin
(
θ
)
=
opp.
hyp.
=
opp.
1
=
opp.
\sin(\theta) = \frac{\text{opp.}}{\text{hyp.}} = \frac{\text{opp.}}{1} = \text{opp.}
sin(θ)=hyp.opp.=1opp.=opp.
同样,余弦是邻边与斜边的比值,斜边为 1,因此余弦变为邻边的实际长度:
cos ( θ ) = adj. hyp. = adj. 1 = adj. \cos(\theta) = \frac{\text{adj.}}{\text{hyp.}} = \frac{\text{adj.}}{1} = \text{adj.} cos(θ)=hyp.adj.=1adj.=adj.

类似地,正切是对边与邻边的比值,只要让邻边为 1,那么正切就变为对边的实际长度:
tan ( θ ) = opp. adj. = opp. 1 = opp \tan(\theta) = \frac{\text{opp.}}{\text{adj.}} = \frac{\text{opp.}}{1} = \text{opp} tan(θ)=adj.opp.=1opp.=opp

因此,构图要清晰,明确让哪条边为 1。单位圆的思想在处理许多三角函数问题时极为巧妙。
其中:
- opp. 表示“对边”(opposite side),即直角三角形中与角 θ \theta θ 对应的边。
- adj. 表示“邻边”(adjacent side),即直角三角形中与角 θ \theta θ 相邻的边。
- hyp. 表示“斜边”(hypotenuse),即直角三角形中最长的边,与直角相对的边。
夹逼定理
通过上述单位圆的简单构图:
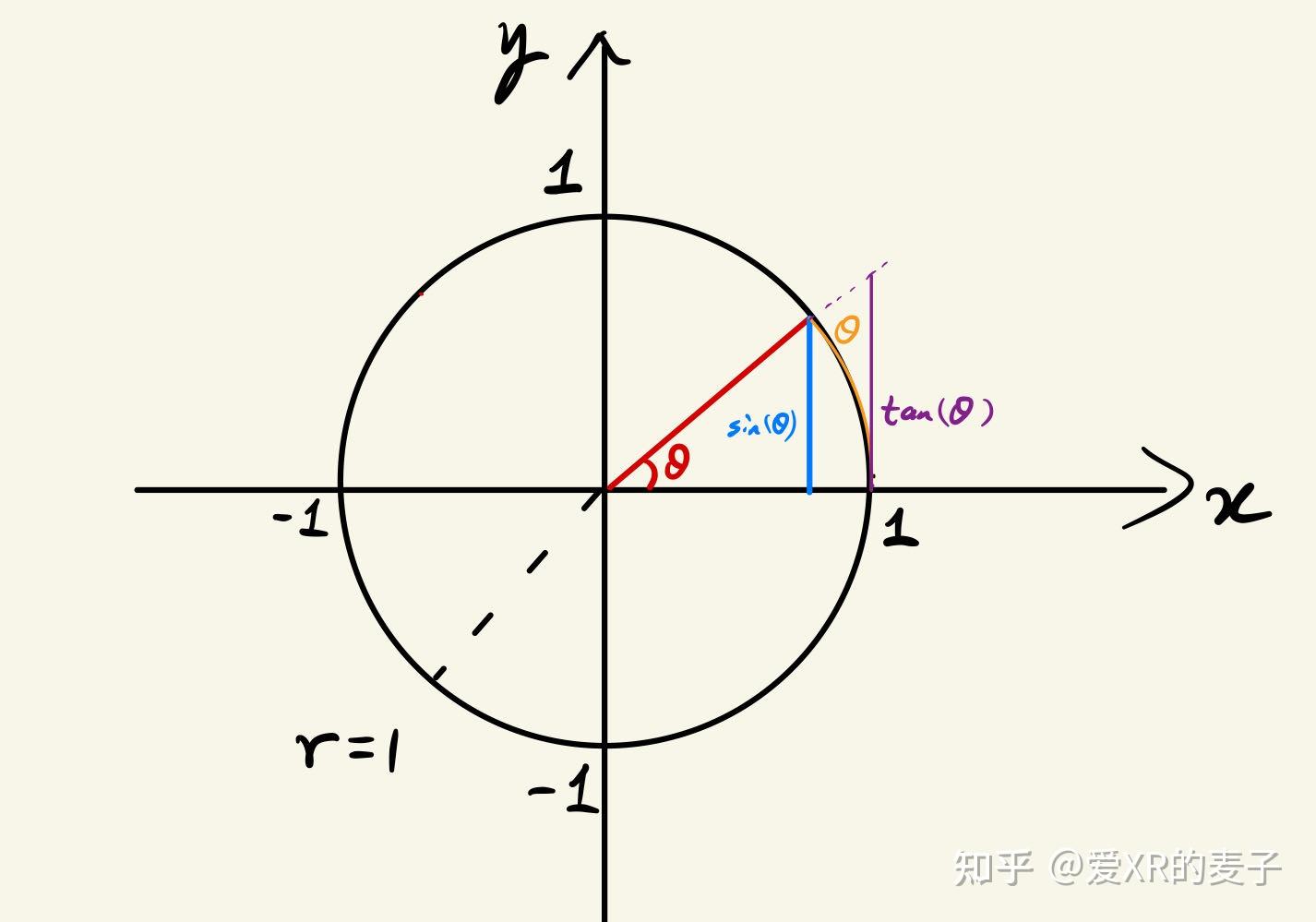
在 0 ≤ θ < π 2 0 \leq \theta < \frac{\pi}{2} 0≤θ<2π 时,有:
sin ( θ ) ≤ θ ≤ tan ( θ ) \sin(\theta) \leq \theta \leq \tan(\theta) sin(θ)≤θ≤tan(θ)
因此,可以进行如下操作:
sin ( θ ) ≤ θ ≤ sin ( θ ) cos ( θ ) \sin(\theta) \leq \theta \leq \frac{\sin(\theta)}{\cos(\theta)} sin(θ)≤θ≤cos(θ)sin(θ)
1 ≤ θ sin ( θ ) ≤ 1 cos ( θ ) 1 \leq \frac{\theta}{\sin(\theta)} \leq \frac{1}{\cos(\theta)} 1≤sin(θ)θ≤cos(θ)1
1 ≥ sin ( θ ) θ ≥ cos ( θ ) 1 \geq \frac{\sin(\theta)}{\theta} \geq \cos(\theta) 1≥θsin(θ)≥cos(θ)
这是一个有趣的不等式,中间项是想要分析的项。当 θ → 0 \theta \rightarrow 0 θ→0 时,知道 cos ( θ ) → 1 \cos(\theta) \rightarrow 1 cos(θ)→1 是确定的,因此中间项既小于等于 1,又大于等于 1,最终只能等于 1。这就是夹逼定理的思想。
因此,得到:
lim h → 0 sin ( k h ) h = k ( lim h → 0 sin ( k h ) k h ) = k ⋅ 1 = k \lim_{h \rightarrow 0} \frac{\sin(k h)}{h} = k \left( \lim_{h \rightarrow 0} \frac{\sin(k h)}{k h} \right) = k \cdot 1 = k h→0limhsin(kh)=k(h→0limkhsin(kh))=k⋅1=k
d f d x = lim h → 0 sin ( k x ) cos ( k h ) − 1 h + cos ( k x ) sin ( k h ) h = k sin ( k x ) ( lim h → 0 cos ( k h ) − 1 k h ) + k cos ( k x ) \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \sin(k x) \frac{\cos(k h) - 1}{h} + \cos(k x) \frac{\sin(k h)}{h} \\ &= k \sin(k x) \left( \lim_{h \rightarrow 0} \frac{\cos(k h) - 1}{k h} \right) + k \cos(k x) \end{aligned} dxdf=h→0limsin(kx)hcos(kh)−1+cos(kx)hsin(kh)=ksin(kx)(h→0limkhcos(kh)−1)+kcos(kx)
还剩下另一部分,可以简单处理如下:
cos ( θ ) − 1 θ \frac{\cos(\theta) - 1}{\theta} θcos(θ)−1
由于 cos 2 ( θ ) + sin 2 ( θ ) = 1 \cos^2(\theta) + \sin^2(\theta) = 1 cos2(θ)+sin2(θ)=1,因此:
( cos ( θ ) − 1 ) ( cos ( θ ) + 1 ) θ ( cos ( θ ) + 1 ) = cos 2 ( θ ) − 1 θ ( cos ( θ ) + 1 ) = − sin ( θ ) θ sin ( θ ) cos ( θ ) + 1 \frac{(\cos(\theta) - 1)(\cos(\theta) + 1)}{\theta (\cos(\theta) + 1)} = \frac{\cos^2(\theta) - 1}{\theta (\cos(\theta) + 1)} = -\frac{\sin(\theta)}{\theta} \frac{\sin(\theta)}{\cos(\theta) + 1} θ(cos(θ)+1)(cos(θ)−1)(cos(θ)+1)=θ(cos(θ)+1)cos2(θ)−1=−θsin(θ)cos(θ)+1sin(θ)
当 θ → 0 \theta \rightarrow 0 θ→0 时, sin ( θ ) θ \frac{\sin(\theta)}{\theta} θsin(θ)、 sin ( θ ) \sin(\theta) sin(θ) 和 cos ( θ ) + 1 \cos(\theta) + 1 cos(θ)+1 分别趋近于 1、0 和 2,整体则趋近于 0。
因此:
d f d x = k sin ( k x ) ( lim h → 0 cos ( k h ) − 1 k h ) + k cos ( k x ) = k sin ( k x ) ⋅ 0 + k cos ( k x ) \begin{aligned} \frac{df}{dx} & =k\sin (kx)\left( \underset{h\to 0}{\mathop{\lim }}\,\frac{\cos (kh)-1}{kh} \right)+k\cos (kx) \\ & =k\sin (kx)\cdot 0+k\cos (kx) \end{aligned} dxdf=ksin(kx)(h→0limkhcos(kh)−1)+kcos(kx)=ksin(kx)⋅0+kcos(kx)
最终结果为:
f ( x ) = sin ( k x ) ⇒ d f d x = k cos ( k x ) f(x) = \sin(k x) \quad \Rightarrow \quad \frac{df}{dx} = k \cos(k x) f(x)=sin(kx)⇒dxdf=kcos(kx)
三角函数(余弦函数)
设函数 f ( x ) = cos ( k x ) f(x) = \cos(k x) f(x)=cos(kx)。
对于余弦函数 (Cosine Function),自然也可以走上面的老路。但也可以复用上面的结论,只要你意识到余弦和正弦之间就是一个 π 2 \frac{\pi}{2} 2π 的相位差,即
f ( x ) = cos ( k x ) = sin ( k x + π 2 ) f(x) = \cos(k x) = \sin(k x + \frac{\pi}{2}) f(x)=cos(kx)=sin(kx+2π)
那么只需要简单的链式法则一下,令 u = k x + π 2 ⇒ d u d x = k u = k x + \frac{\pi}{2} \Rightarrow \frac{du}{dx} = k u=kx+2π⇒dxdu=k,
f ( u ) = sin ( u ) ⇒ d f d u = cos ( u ) f(u) = \sin(u) \Rightarrow \frac{df}{du} = \cos(u) f(u)=sin(u)⇒dudf=cos(u)
因此,
d f d x = d f d u d u d x = k cos ( k x + π 2 ) \frac{df}{dx} = \frac{df}{du} \frac{du}{dx} = k \cos(k x + \frac{\pi}{2}) dxdf=dudfdxdu=kcos(kx+2π)
而如果 cos \cos cos 函数再往 − x -x −x 方向移动 π 2 \frac{\pi}{2} 2π 个单位的话,那么就变成 − sin -\sin −sin 了,所以,
f ( x ) = cos ( k x ) ⇒ d f d x = − k sin ( k x ) f(x) = \cos(k x) \quad \Rightarrow \quad \frac{df}{dx} = -k \sin(k x) f(x)=cos(kx)⇒dxdf=−ksin(kx)
三角函数(正切函数)
正切函数 (Tangent Function)
设函数 f ( x ) = tan ( k x ) f(x) = \tan(k x) f(x)=tan(kx)。
正切函数这里引入微积分另一个重要的法则:乘法法则 (Product Rule)。
乘法法则
如果 f ( x ) = u ( x ) v ( x ) f(x) = u(x) v(x) f(x)=u(x)v(x),那么如何求得 d f d x \frac{df}{dx} dxdf?代入
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 u ( x + h ) v ( x + h ) − u ( x ) v ( x ) h = lim h → 0 u ( x + h ) v ( x + h ) − u ( x ) v ( x ) + u ( x ) v ( x + h ) − u ( x ) v ( x + h ) h = lim h → 0 u ( x + h ) v ( x + h ) − u ( x ) v ( x + h ) h + u ( x ) v ( x + h ) − u ( x ) v ( x ) h = lim h → 0 u ( x + h ) − u ( x ) h v ( x + h ) + u ( x ) v ( x + h ) − v ( x ) h \begin{aligned} \frac{df}{dx} &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{u(x + h) v(x + h) - u(x) v(x)}{h}\\ &= \lim_{h \rightarrow 0} \frac{u(x + h) v(x + h) - u(x) v(x) + u(x) v(x + h) - u(x) v(x + h)}{h}\\ &= \lim_{h \rightarrow 0} \frac{u(x + h) v(x + h) - u(x) v(x + h)}{h} + \frac{u(x) v(x + h) - u(x) v(x)}{h}\\ &= \lim_{h \rightarrow 0} \frac{u(x + h) - u(x)}{h} v(x + h) + u(x) \frac{v(x + h) - v(x)}{h} \end{aligned} dxdf=h→0limhf(x+h)−f(x)=h→0limhu(x+h)v(x+h)−u(x)v(x)=h→0limhu(x+h)v(x+h)−u(x)v(x)+u(x)v(x+h)−u(x)v(x+h)=h→0limhu(x+h)v(x+h)−u(x)v(x+h)+hu(x)v(x+h)−u(x)v(x)=h→0limhu(x+h)−u(x)v(x+h)+u(x)hv(x+h)−v(x)
可以看出,前一项中
lim h → 0 u ( x + h ) − u ( x ) h = d u d x \lim_{h \rightarrow 0} \frac{u(x + h) - u(x)}{h} = \frac{du}{dx} h→0limhu(x+h)−u(x)=dxdu
lim h → 0 v ( x + h ) = v ( x ) \lim_{h \rightarrow 0} v(x + h) = v(x) h→0limv(x+h)=v(x)
第二项中
lim h → 0 v ( x + h ) − v ( x ) h = d v d x \lim_{h \rightarrow 0} \frac{v(x + h) - v(x)}{h} = \frac{dv}{dx} h→0limhv(x+h)−v(x)=dxdv
因此,最终结果为:
f ( x ) = u ( x ) v ( x ) ⇒ d f d x = u v ′ + u ′ v f(x) = u(x) v(x) \quad \Rightarrow \quad \frac{df}{dx} = u v' + u' v f(x)=u(x)v(x)⇒dxdf=uv′+u′v
除法法则
除法法则 (Quotient Rule) 是一个我从未背过,也觉得没必要背的法则。用乘法法则去解决并不比除法法则多几步操作,而且除法法则公式中还有负号,就像之前说的,背反就前功尽弃。
这里写下是为了等下用,但其实就可以当成做了一次乘法法则。
如果 f ( x ) = u ( x ) v ( x ) f(x) = \frac{u(x)}{v(x)} f(x)=v(x)u(x),去求 d f d x \frac{df}{dx} dxdf,
本质上, f ( x ) = u ( x ) v ( x ) = u ( x ) ( v ( x ) ) − 1 f(x) = \frac{u(x)}{v(x)} = u(x) (v(x))^{-1} f(x)=v(x)u(x)=u(x)(v(x))−1,所以
d f d x = u d d x ( v − 1 ) + d u d x v − 1 = u d d v ( v − 1 ) d v d x + d u d x 1 v = − u 1 v 2 d v d x + d u d x 1 v \begin{aligned} \frac{df}{dx} & =u\frac{d}{dx}\left( {{v}^{-1}} \right)+\frac{du}{dx}{{v}^{-1}} \\ & =u\frac{d}{dv}\left( {{v}^{-1}} \right)\frac{dv}{dx}+\frac{du}{dx}\frac{1}{v} \\ & =-u\frac{1}{{{v}^{2}}}\frac{dv}{dx}+\frac{du}{dx}\frac{1}{v} \end{aligned} dxdf=udxd(v−1)+dxduv−1=udvd(v−1)dxdv+dxduv1=−uv21dxdv+dxduv1
因此,
f ( x ) = u ( x ) v ( x ) ⇒ d f d x = v u ′ − u v ′ v 2 f(x) = \frac{u(x)}{v(x)} \quad \Rightarrow \quad \frac{df}{dx} = \frac{v u' - u v'}{v^2} f(x)=v(x)u(x)⇒dxdf=v2vu′−uv′
回到推导,因为
f ( x ) = tan ( k x ) = sin ( k x ) cos ( k x ) f(x) = \tan(k x) = \frac{\sin(k x)}{\cos(k x)} f(x)=tan(kx)=cos(kx)sin(kx)
令 u = sin ( k x ) u = \sin(k x) u=sin(kx), v = cos ( k x ) v = \cos(k x) v=cos(kx),所以
d f d x = v u ′ − u v ′ v 2 = cos ( k x ) k cos ( k x ) − sin ( k x ) k ( − sin ( k x ) ) cos 2 ( k x ) = k cos 2 ( k x ) + sin 2 ( k x ) cos 2 ( k x ) = k 1 cos 2 ( k x ) \begin{aligned} \frac{df}{dx} & =\frac{v{u}'-u{v}'}{{{v}^{2}}} \\ & =\frac{\cos (kx)k\cos (kx)-\sin (kx)k(-\sin (kx))}{{{\cos }^{2}}(kx)} \\ & =k\frac{{{\cos }^{2}}(kx)+{{\sin }^{2}}(kx)}{{{\cos }^{2}}(kx)}=k\frac{1}{{{\cos }^{2}}(kx)} \end{aligned} dxdf=v2vu′−uv′=cos2(kx)cos(kx)kcos(kx)−sin(kx)k(−sin(kx))=kcos2(kx)cos2(kx)+sin2(kx)=kcos2(kx)1
因此,
f ( x ) = tan ( k x ) ⇒ d f d x = k sec 2 ( k x ) f(x) = \tan(k x) \quad \Rightarrow \quad \frac{df}{dx} = k \sec^2(k x) f(x)=tan(kx)⇒dxdf=ksec2(kx)
至此,主要的三个三角函数的微分已经完成。其余的三角函数(如正割、余割、余切)分别是前三者的倒数,因此只需多代一次链式法则即可。
指数函数
指数函数 (Exponential Function)
设函数 f ( x ) = a λ x f(x) = a^{\lambda x} f(x)=aλx,其中 a a a 和 λ \lambda λ 是常数。
按照之前的流程:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 a λ ( x + h ) − a λ x h = lim h → 0 a λ x a λ h − a λ x h = a λ x lim h → 0 a λ h − 1 h \frac{df}{dx} = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} = \lim_{h \rightarrow 0} \frac{a^{\lambda (x + h)} - a^{\lambda x}}{h} = \lim_{h \rightarrow 0} \frac{a^{\lambda x} a^{\lambda h} - a^{\lambda x}}{h} = a^{\lambda x} \lim_{h \rightarrow 0} \frac{a^{\lambda h} - 1}{h} dxdf=h→0limhf(x+h)−f(x)=h→0limhaλ(x+h)−aλx=h→0limhaλxaλh−aλx=aλxh→0limhaλh−1
从最后的表达式中可以看出,指数函数具有一个神奇的性质:
d f d x ∝ f \frac{df}{dx} \propto f dxdf∝f
自然常数
当然,遇到这种情况,大家一定会去寻找一个最特殊的情况,即
d f d x = f \frac{df}{dx} = f dxdf=f
换言之,
lim h → 0 a λ h − 1 h = 1 \lim_{h \rightarrow 0} \frac{a^{\lambda h} - 1}{h} = 1 h→0limhaλh−1=1
这里先默认 λ = 1 \lambda = 1 λ=1,原因有二:一是 λ \lambda λ 之后可以通过链式法则解决;二是更重要的是,只有一个公式,无法同时解两个变量。
lim h → 0 a h − 1 h = 1 \lim_{h \rightarrow 0} \frac{a^{h} - 1}{h} = 1 h→0limhah−1=1
lim h → 0 a h = lim h → 0 h + 1 \lim_{h \rightarrow 0} a^{h} = \lim_{h \rightarrow 0} h + 1 h→0limah=h→0limh+1
两边同时开方:
lim h → 0 a h = lim h → 0 h + 1 \lim_{h \rightarrow 0} a^{h} = \lim_{h \rightarrow 0} h + 1 h→0limah=h→0limh+1
a = lim h → 0 ( h + 1 ) 1 h a = \lim_{h \rightarrow 0} (h + 1)^{\frac{1}{h}} a=h→0lim(h+1)h1
这是一个什么数字呢?
可以做如下变换,令 h = 1 N h = \frac{1}{N} h=N1,这样当 h → 0 h \rightarrow 0 h→0 时等效于 N → ∞ N \rightarrow \infty N→∞(假设 h h h 从数轴正半轴趋近于 0),因此:
a = lim N → ∞ ( 1 + 1 N ) N a = \lim_{N \rightarrow \infty} \left(1 + \frac{1}{N}\right)^{N} a=N→∞lim(1+N1)N
接下来列出一个表格:
| N N N | a a a |
|---|---|
| 1 | 2.0 |
| 10 | 2.593742 |
| 1,000 | 2.716924 |
| 1,000,000 | 2.718280 |
| 1,000,000,000 | 2.718282 |
可以看出这个数值趋近于 2.718 几,而这个数就是对诸多领域都极为关键的自然常数 (Natural Constant) e e e,当然,也叫欧拉数 (Euler’s Number)。没办法,欧拉真是无处不在。
而
e = lim N → ∞ ( 1 + 1 N ) N e = \lim_{N \rightarrow \infty} \left(1 + \frac{1}{N}\right)^{N} e=N→∞lim(1+N1)N
也可以被视为欧拉数的定义。
但对于目前而言,这个欧拉数最大的意义是,以它为底时的微分是它自己本身(如果 λ = 1 \lambda = 1 λ=1 的话),加上链式法则,就有:
f ( x ) = e λ x ⇒ d f d x = λ e λ x f(x) = e^{\lambda x} \quad \Rightarrow \quad \frac{df}{dx} = \lambda e^{\lambda x} f(x)=eλx⇒dxdf=λeλx
那么对于一般的 a ≠ e a \neq e a=e 呢?两边同时取对数即可。
对数函数 (Logarithmic Function) 是指数函数的逆运算。也就是说,
f ( x ) = y = a x ⇒ log a ( y ) = x ⇒ f − 1 ( x ) = y = log a ( x ) f(x) = y = a^{x} \quad \Rightarrow \quad \log_{a}(y) = x \quad \Rightarrow \quad f^{-1}(x) = y = \log_{a}(x) f(x)=y=ax⇒loga(y)=x⇒f−1(x)=y=loga(x)
而如果底数为欧拉数 e e e,即 log e \log_{e} loge,那么在物理学中通常写作 ln \ln ln,也就是自然对数 (Natural Logarithm)。而在计算机领域中,许多地方直接写作 log \log log,例如 NumPy log 函数(当然,在计算机领域中,如果看到有人直接使用 log \log log,最好问清楚其具体含义,因为有时默认底数为 2 或 10)。
回过头来,
f ( x ) = a λ x = e ln ( a ) λ x f(x) = a^{\lambda x} = e^{\ln(a) \lambda x} f(x)=aλx=eln(a)λx
因此,
f ( x ) = a λ x ⇒ d f d x = λ ln ( a ) a λ x f(x) = a^{\lambda x} \quad \Rightarrow \quad \frac{df}{dx} = \lambda \ln(a) a^{\lambda x} f(x)=aλx⇒dxdf=λln(a)aλx
对数函数
设函数 f ( x ) = log a ( λ x ) f(x) = \log_{a}(\lambda x) f(x)=loga(λx)。
同样,先讨论比较特殊的情况,即自然对数的情况。
设 f ( x ) = ln ( λ x ) f(x) = \ln(\lambda x) f(x)=ln(λx)。基本上,这个推导大家都会心照不宣地选择隐函数微分,此处也采用这种方法:
y = ln ( λ x ) ⇒ e y = λ x ⇒ d d x ( e y ) = d d x ( λ x ) ⇒ d d y ( e y ) d y d x = λ ⇒ e y d y d x = λ ⇒ λ x d y d x = λ ⇒ d y d x = 1 x \begin{aligned} y & =\ln (\lambda x)\quad \\ & \Rightarrow \quad {{e}^{y}}=\lambda x\quad \\ & \Rightarrow \quad \frac{d}{dx}({{e}^{y}})=\frac{d}{dx}(\lambda x)\quad \\ & \Rightarrow \quad \frac{d}{dy}({{e}^{y}})\frac{dy}{dx}=\lambda \quad \\ & \Rightarrow \quad {{e}^{y}}\frac{dy}{dx}=\lambda \quad \\ & \Rightarrow \quad \lambda x\frac{dy}{dx}=\lambda \quad \\ & \Rightarrow \quad \frac{dy}{dx}=\frac{1}{x} \end{aligned} y=ln(λx)⇒ey=λx⇒dxd(ey)=dxd(λx)⇒dyd(ey)dxdy=λ⇒eydxdy=λ⇒λxdxdy=λ⇒dxdy=x1
那么对于一般的 a a a 的情况,就需要用到换底公式了。
换底公式
我始终认为有一些公式被创造出来就是让人背的。我并不觉得记住这种公式能提升多少计算速度,但它被当作一个公式搞得煞有介事。换底公式就是这样的公式之一。
如果
k
=
log
a
(
c
)
⇒
a
k
=
c
⇒
log
b
(
a
k
)
=
log
b
(
c
)
⇒
k
log
b
(
a
)
=
log
b
(
c
)
⇒
k
=
log
b
(
c
)
log
b
(
a
)
\begin{aligned} k&={{\log }_{a}}(c)\quad \\ & \Rightarrow \quad {{a}^{k}}=c\quad \\ & \Rightarrow \quad {{\log }_{b}}({{a}^{k}})={{\log }_{b}}(c)\quad \\ & \Rightarrow \quad k{{\log }_{b}}(a)={{\log }_{b}}(c)\quad \\ & \Rightarrow \quad k=\frac{{{\log }_{b}}(c)}{{{\log }_{b}}(a)} \\ \end{aligned}
k=loga(c)⇒ak=c⇒logb(ak)=logb(c)⇒klogb(a)=logb(c)⇒k=logb(a)logb(c)
这就是所谓的换底公式:
log a ( c ) = log b ( c ) log b ( a ) \log_{a}(c) = \frac{\log_{b}(c)}{\log_{b}(a)} loga(c)=logb(a)logb(c)
代入换底公式:
f ( x ) = log a ( λ x ) = ln ( λ x ) ln ( a ) f(x) = \log_{a}(\lambda x) = \frac{\ln(\lambda x)}{\ln(a)} f(x)=loga(λx)=ln(a)ln(λx)
因此,
f ( x ) = log a ( λ x ) ⇒ d f d x = 1 ln ( a ) ⋅ 1 x f(x) = \log_{a}(\lambda x) \quad \Rightarrow \quad \frac{df}{dx} = \frac{1}{\ln(a)} \cdot \frac{1}{x} f(x)=loga(λx)⇒dxdf=ln(a)1⋅x1
双曲三角函数
关于双曲三角函数 (Hyperbolic Trigonometric Functions),最好先一口气把定义放出来。
双曲余弦函数
双曲余弦函数 (Hyperbolic Cosine Function)
f ( x ) = cosh ( k x ) = e k x + e − k x 2 f(x) = \cosh(k x) = \frac{e^{k x} + e^{-k x}}{2} f(x)=cosh(kx)=2ekx+e−kx
双曲正弦函数
双曲正弦函数 (Hyperbolic Sine Function)
f ( x ) = sinh ( k x ) = e k x − e − k x 2 f(x) = \sinh(k x) = \frac{e^{k x} - e^{-k x}}{2} f(x)=sinh(kx)=2ekx−e−kx
双曲正切函数
双曲正切函数 (Hyperbolic Tangent Function)
f ( x ) = tanh ( k x ) = sinh ( k x ) cosh ( k x ) = e k x − e − k x e k x + e − k x = e 2 k x − 1 e 2 k x + 1 \begin{aligned} f(x) &= \tanh(k x) \\ &= \frac{\sinh(k x)}{\cosh(k x)} \\ &= \frac{e^{k x} - e^{-k x}}{e^{k x} + e^{-k x}} \\ &= \frac{e^{2 k x} - 1}{e^{2 k x} + 1} \end{aligned} f(x)=tanh(kx)=cosh(kx)sinh(kx)=ekx+e−kxekx−e−kx=e2kx+1e2kx−1
其实写到这里有点多余,因为有了上面的定义,只需使用基本的链式法则和乘法法则即可解决。
所以这里只做双曲正切函数的推导:
f ( x ) = tanh ( k x ) = e k x − e − k x e k x + e − k x f(x) = \tanh(k x) = \frac{e^{k x} - e^{-k x}}{e^{k x} + e^{-k x}} f(x)=tanh(kx)=ekx+e−kxekx−e−kx
d f d x = d d x ( e k x − e − k x ) ⋅ 1 e k x + e − k x + ( e k x − e − k x ) ⋅ d d x ( 1 e k x + e − k x ) = k ( e k x + e − k x ) ⋅ 1 e k x + e − k x − ( e k x − e − k x ) ⋅ d d x ( e k x + e − k x ) ⋅ 1 ( e k x + e − k x ) 2 = k ⋅ 1 − ( e k x − e − k x ) ⋅ k ( e k x − e − k x ) ( e k x + e − k x ) 2 = k − k ( e k x − e − k x ) 2 ( e k x + e − k x ) 2 = k ( ( e k x + e − k x ) 2 − ( e k x − e − k x ) 2 ( e k x + e − k x ) 2 ) = k ( e 2 k x + 2 + e − 2 k x − ( e 2 k x − 2 + e − 2 k x ) ( e k x + e − k x ) 2 ) = k ( 4 ( e k x + e − k x ) 2 ) = k ( 2 e k x + e − k x ) 2 = k 1 cosh 2 ( k x ) \begin{aligned} \frac{df}{dx} &= \frac{d}{dx}(e^{k x} - e^{-k x}) \cdot \frac{1}{e^{k x} + e^{-k x}} + (e^{k x} - e^{-k x}) \cdot \frac{d}{dx}\left(\frac{1}{e^{k x} + e^{-k x}}\right) \\ &= k \left( e^{k x} + e^{-k x} \right) \cdot \frac{1}{e^{k x} + e^{-k x}} - (e^{k x} - e^{-k x}) \cdot \frac{d}{dx}(e^{k x} + e^{-k x}) \cdot \frac{1}{(e^{k x} + e^{-k x})^2} \\ &= k \cdot 1 - \frac{(e^{k x} - e^{-k x}) \cdot k (e^{k x} - e^{-k x})}{(e^{k x} + e^{-k x})^2} \\ &= k - k \frac{(e^{k x} - e^{-k x})^2}{(e^{k x} + e^{-k x})^2} \\ &= k \left( \frac{(e^{k x} + e^{-k x})^2 - (e^{k x} - e^{-k x})^2}{(e^{k x} + e^{-k x})^2} \right) \\ &= k \left( \frac{e^{2 k x} + 2 + e^{-2 k x} - (e^{2 k x} - 2 + e^{-2 k x})}{(e^{k x} + e^{-k x})^2} \right) \\ &= k \left( \frac{4}{(e^{k x} + e^{-k x})^2} \right) \\ &= k \left( \frac{2}{e^{k x} + e^{-k x}} \right)^2 \\ &= k \frac{1}{\cosh^2(k x)} \end{aligned} dxdf=dxd(ekx−e−kx)⋅ekx+e−kx1+(ekx−e−kx)⋅dxd(ekx+e−kx1)=k(ekx+e−kx)⋅ekx+e−kx1−(ekx−e−kx)⋅dxd(ekx+e−kx)⋅(ekx+e−kx)21=k⋅1−(ekx+e−kx)2(ekx−e−kx)⋅k(ekx−e−kx)=k−k(ekx+e−kx)2(ekx−e−kx)2=k((ekx+e−kx)2(ekx+e−kx)2−(ekx−e−kx)2)=k((ekx+e−kx)2e2kx+2+e−2kx−(e2kx−2+e−2kx))=k((ekx+e−kx)24)=k(ekx+e−kx2)2=kcosh2(kx)1
双曲三角函数的命名与三角函数一致,因此可以简单地写成:
f ( x ) = tanh ( k x ) ⇒ d f d x = k s e c h 2 ( k x ) f(x) = \tanh(k x) \quad \Rightarrow \quad \frac{df}{dx} = k \, \mathbf{sech}^{2}(k x) f(x)=tanh(kx)⇒dxdf=ksech2(kx)
编辑于 2024-03-09 16:28・上海
via:
- 【回归本源】给微积分入门者的小记 - 知乎
https://zhuanlan.zhihu.com/p/609087301- 圆周率的神奇算法【官方双语】【Veritasium真理元素】_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1x64y1D7Rn/
- 圆周率的神奇算法【官方双语】【Veritasium真理元素】_哔哩哔哩_bilibili





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








