数学教育 | Birds and Frogs

注：本文为 “Birds and Frogs” 相关合辑。
英文引文，机翻未校。
中文引文，略作重排。
如有内容异常，请看原文。

---

Birds and Frogs

鸟与青蛙

Freeman Dyson

Some mathematicians are birds, others are frogs. Birds fly high in the air and survey broad vistas of mathematics out to the far horizon. They delight in concepts that unify our thinking and bring together diverse problems from different parts of the landscape. Frogs live in the mud below and see only the flowers that grow nearby. They delight in the details of particular objects, and they solve problems one at a time. I happen to be a frog, but many of my best friends are birds. The main theme of my talk tonight is this. Mathematics needs both birds and frogs. Mathematics is rich and beautiful because birds give it broad visions and frogs give it intricate details. Mathematics is both great art and important science, because it combines generality of concepts with depth of structures. It is stupid to claim that birds are better than frogs because they see farther, or that frogs are better than birds because they see deeper. The world of mathematics is both broad and deep, and we need birds and frogs working together to explore it.
有些数学家是鸟，另一些则是青蛙。鸟在高空翱翔，俯瞰数学的广阔远景，直至遥远的地平线。它们热衷于能统一我们思想的概念，将来自这片领域不同部分的各种问题联系起来。青蛙则生活在下方的泥沼中，只看见身边生长的花朵。它们沉醉于特定事物的细节，逐个解决问题。我恰好是一只青蛙，但我许多最好的朋友是鸟。今晚我演讲的主旨是：数学既需要鸟，也需要青蛙。数学之所以丰富而美丽，是因为鸟为它提供广阔的视野，青蛙为它填充复杂的细节。数学既是伟大的艺术，也是重要的科学，因为它将概念的普遍性与结构的深刻性融为一体。声称鸟比青蛙好因为它们看得更远，或是青蛙比鸟好因为它们看得更深，都是愚蠢的。数学的世界既广阔又深邃，我们需要鸟和青蛙共同努力去探索。

This talk is called the Einstein lecture, and I am grateful to the American Mathematical Society for inviting me to do honor to Albert Einstein. Einstein was not a mathematician, but a physicist who had mixed feelings about mathematics. On the one hand, he had enormous respect for the power of mathematics to describe the workings of nature, and he had an instinct for mathematical beauty which led him onto the right track to find nature’s laws. On the other hand, he had no interest in pure mathematics, and he had no technical skill as a mathematician. In his later years he hired younger colleagues with the title of assistants to do mathematical calculations for him. His way of thinking was physical rather than mathematical. He was supreme among physicists as a bird who saw further than others. I will not talk about Einstein since I have nothing new to say.
本次演讲名为“爱因斯坦讲座”，我感谢美国数学会邀请我来向阿尔伯特·爱因斯坦致敬。爱因斯坦不是数学家，而是一位对数学感情复杂的物理学家。一方面，他对数学描述自然运作的力量怀有极大敬意，并且他对数学之美有着直觉，这引导他走上了发现自然规律的正确道路。另一方面，他对纯数学毫无兴趣，也没有专业的数学技能。晚年时，他聘请了年轻的同事担任助手，为他进行数学计算。他的思维方式是物理的，而非数学的。在物理学家中，他是一只看得比别人更远的卓越的鸟。我不会过多谈论爱因斯坦，因为我没有什么新内容可讲。

Francis Bacon and René Descartes
弗朗西斯·培根与勒内·笛卡尔

At the beginning of the seventeenth century, two great philosophers, Francis Bacon in England and René Descartes in France, proclaimed the birth of modern science. Descartes was a bird, and Bacon was a frog. Each of them described his vision of the future. Their visions were very different. Bacon said, “All depends on keeping the eye steadily fixed on the facts of nature.” Descartes said, “I think, therefore I am.” According to Bacon, scientists should travel over the earth collecting facts, until the accumulated facts reveal how Nature works. The scientists will then induce from the facts the laws that Nature obeys. According to Descartes, scientists should stay at home and deduce the laws of Nature by pure thought. In order to deduce the laws correctly, the scientists will need only the rules of logic and knowledge of the existence of God. For four hundred years since Bacon and Descartes led the way, science has raced ahead by following both paths simultaneously. Neither Baconian empiricism nor Cartesian dogmatism has the power to elucidate Nature’s secrets by itself, but both together have been amazingly successful. For four hundred years English scientists have tended to be Baconian and French scientists Cartesian. Faraday and Darwin and Rutherford were Baconians; Pascal and Laplace and Poincaré were Cartesians. Science was greatly enriched by the cross-fertilization of the two contrasting cultures. Both cultures were always at work in both countries. Newton was at heart a Cartesian, using pure thought as Descartes intended, and using it to demolish the Cartesian dogma of vortices. Marie Curie was at heart a Baconian, boiling tons of crude uranium ore to demolish the dogma of the indestructibility of atoms.
17世纪初，两位伟大的哲学家——英国的弗朗西斯·培根和法国的勒内·笛卡尔——宣告了现代科学的诞生。笛卡尔是鸟，培根是青蛙。他们各自描绘了对未来的愿景，且这些愿景大相径庭。培根说：“一切都取决于始终紧盯自然的事实。”笛卡尔说：“我思故我在。”根据培根的观点，科学家应该走遍世界收集事实，直到积累的事实揭示自然的运作方式。然后，科学家将从这些事实中归纳出自然所遵循的规律。根据笛卡尔的观点，科学家应该待在家里，通过纯粹的思考演绎自然规律。为了正确地演绎规律，科学家只需要逻辑规则和对上帝存在的认知。自培根和笛卡尔开辟道路以来的四百年里，科学通过同时遵循这两条路径飞速发展。无论是培根式的经验主义，还是笛卡尔式的教条主义，都无法单独揭示自然的奥秘，但两者结合却取得了惊人的成功。四百年来，英国科学家倾向于培根传统，法国科学家倾向于笛卡尔传统。法拉第、达尔文和卢瑟福是培根主义者；帕斯卡、拉普拉斯和庞加莱是笛卡尔主义者。这两种对比鲜明的文化的交叉融合，极大地丰富了科学。这两种文化在两个国家都一直发挥着作用。牛顿本质上是笛卡尔主义者，他像笛卡尔所倡导的那样运用纯粹的思考，并以此推翻了笛卡尔的涡旋教条。玛丽·居里本质上是培根主义者，她通过煮沸数吨粗铀矿石，推翻了原子不可毁灭的教条。

Freeman Dyson is an emeritus professor in the School of Natural Sciences, Institute for Advanced Study, Princeton, NJ. His email address is dyson@ias.edu.
弗里曼·戴森是普林斯顿高等研究院自然科学学院的名誉教授，地址为新泽西州普林斯顿。他的电子邮箱是dyson@ias.edu。
 
This article is a written version of his AMS Einstein Lecture, which was to have been given in October 2008 but which unfortunately had to be canceled.
本文是他在美国数学会爱因斯坦讲座的讲稿，该讲座原定于2008年10月举行，但不幸被迫取消。

In the history of twentieth century mathematics, there were two decisive events, one belonging to the Baconian tradition and the other to the Cartesian tradition. The first was the International Congress of Mathematicians in Paris in 1900, at which Hilbert gave the keynote address, charting the course of mathematics for the coming century by propounding his famous list of twenty-three outstanding unsolved problems. Hilbert himself was a bird, flying high over the whole territory of mathematics, but he addressed his problems to the frogs who would solve them one at a time. The second decisive event was the formation of the Bourbaki group of mathematical birds in France in the 1930s, dedicated to publishing a series of textbooks that would establish a unifying framework for all of mathematics. The Hilbert problems were enormously successful in guiding mathematical research into fruitful directions. Some of them were solved and some remain unsolved, but almost all of them stimulated the growth of new ideas and new fields of mathematics. The Bourbaki project was equally influential. It changed the style of mathematics for the next fifty years, imposing a logical coherence that did not exist before, and moving the emphasis from concrete examples to abstract generalities. In the Bourbaki scheme of things, mathematics is the abstract structure included in the Bourbaki textbooks. What is not in the textbooks is not mathematics. Concrete examples, since they do not appear in the textbooks, are not mathematics. The Bourbaki program was the extreme expression of the Cartesian style. It narrowed the scope of mathematics by excluding the beautiful flowers that Baconian travelers might collect by the wayside.
在20世纪数学史上，有两个决定性事件，一个属于培根传统，另一个属于笛卡尔传统。第一个是1900年在巴黎举行的国际数学家大会，希尔伯特在会上发表了主题演讲，通过提出著名的23个未解决的重大问题，为未来一个世纪的数学发展指明了方向。希尔伯特本人是一只鸟，在整个数学领域的高空翱翔，但他将这些问题交给了青蛙们，让它们逐个解决。第二个决定性事件是20世纪30年代法国数学鸟类群体“布尔巴基学派”的成立，该学派致力于出版一系列教科书，为整个数学建立一个统一的框架。希尔伯特的问题在引导数学研究走向富有成果的方向上取得了巨大成功。其中一些问题已被解决，一些仍未解决，但几乎所有问题都刺激了新思想和新数学领域的发展。布尔巴基项目同样具有影响力。它改变了未来50年的数学风格，赋予了数学一种前所未有的逻辑连贯性，并将重点从具体实例转向抽象的普遍性。在布尔巴基的体系中，数学是包含在布尔巴基教科书中的抽象结构。不在教科书中的内容就不是数学。具体的例子，由于没有出现在教科书中，也不是数学。布尔巴基纲领是笛卡尔风格的极端表现。它排除了培根式的探索者可能在路边收集到的美丽花朵，从而窄化了数学的范围。

Jokes of Nature

自然的玩笑

For me, as a Baconian, the main thing missing in the Bourbaki program is the element of surprise. The Bourbaki program tried to make mathematics logical. When I look at the history of mathematics, I see a succession of illogical jumps, improbable coincidences, jokes of nature. One of the most profound jokes of nature is the square root of minus one that the physicist Erwin Schrödinger put into his wave equation when he invented
对我这个培根主义者来说，布尔巴基纲领中缺少的主要东西是惊喜元素。布尔巴基纲领试图让数学变得合乎逻辑。但当我审视数学史时，我看到的是一连串不合逻辑的跳跃、不太可能的巧合，也就是“自然的玩笑”。其中最深刻的“自然的玩笑”之一，是物理学家埃尔温·薛定谔在1926年发明

wave mechanics in 1926. Schrödinger was a bird who started from the idea of unifying mechanics with optics. A hundred years earlier, Hamilton had unified classical mechanics with ray optics, using the same mathematics to describe optical rays and classical particle trajectories. Schrödinger’s idea was to extend this unification to wave optics and wave mechanics. Wave optics already existed, but wave mechanics did not. Schrödinger had to invent wave mechanics to complete the unification. Starting from wave optics as a model, he wrote down a differential equation for a mechanical particle, but the equation made no sense. The equation looked like the equation of conduction of heat in a continuous medium. Heat conduction has no visible relevance to particle mechanics. Schrödinger’s idea seemed to be going nowhere. But then came the surprise. Schrödinger put the square root of minus one into the equation, and suddenly it made sense. Suddenly it became a wave equation instead of a heat conduction equation. And Schrödinger found to his delight that the equation has solutions corresponding to the quantized orbits in the Bohr model of the atom.
波动力学时，在他的波动方程中引入的负一的平方根。薛定谔是一只鸟，他从统一力学和光学的想法出发。一百年前，哈密顿已经将经典力学与几何光学统一起来，用同样的数学描述光线和经典粒子的轨迹。薛定谔的想法是将这种统一扩展到波动光学和波动力学。波动光学已经存在，但波动力学尚未诞生。薛定谔必须发明波动力学来完成这种统一。他以波动光学为模型，为力学粒子写下了一个微分方程，但这个方程毫无意义。这个方程看起来像连续介质中的热传导方程。而热传导与粒子力学显然没有关联。薛定谔的想法似乎走进了死胡同。但随后惊喜出现了。薛定谔将负一的平方根代入方程，方程突然就有了意义。它一下子从热传导方程变成了波动方程。薛定谔欣喜地发现，这个方程的解与玻尔原子模型中的量子化轨道相对应。

Francis Bacon
弗朗西斯·培根

René Descartes
勒内·笛卡尔

It turns out that the Schrödinger equation describes correctly everything we know about the behavior of atoms. It is the basis of all of chemistry and most of physics. And that square root of minus one means that nature works with complex numbers and not with real numbers. This discovery came as a complete surprise, to Schrödinger as well as to everybody else. According to Schrödinger, his fourteen-year-old girl friend Itha Junger said to him at the time, “Hey, you never even thought when you began that so much sensible stuff would come out of it.” All through the nineteenth century, mathematicians from Abel to Riemann and Weierstrass had been creating a magnificent theory of functions of complex variables. They had discovered that the theory of functions became far deeper and more powerful when it was extended from real to complex numbers. But they always thought of complex numbers as an artificial construction, invented by human mathematicians as a useful and elegant abstraction from real life. It never entered their heads that this artificial number system that they had invented was in fact the ground on which atoms move. They never imagined that nature had got there first.
事实证明，薛定谔方程正确地描述了我们所知道的关于原子行为的一切。它是整个化学和大部分物理学的基础。而那个负一的平方根意味着，自然界运用的是复数，而非实数。这一发现让薛定谔和其他所有人都完全始料未及。据薛定谔说，他当时14岁的女友伊莎·荣格对他说：“嘿，你一开始根本没想到会从中得出这么多有意义的东西吧。”整个19世纪，从阿贝尔到黎曼再到魏尔斯特拉斯，数学家们一直在构建宏伟的复变函数理论。他们发现，当函数理论从实数扩展到复数时，会变得更加深刻和强大。但他们一直认为复数是一种人为构造，是人类数学家从现实生活中抽象出来的有用且优雅的概念。他们从未想过，自己发明的这种人为的数系，实际上是原子运动的基础。他们从未想过，自然界早已捷足先登。

Another joke of nature is the precise linearity of quantum mechanics, the fact that the possible states of any physical object form a linear space.
另一个“自然的玩笑”是量子力学的精确线性性，即任何物理对象的可能状态构成一个线性空间。

Before quantum mechanics was invented, classical physics was always nonlinear, and linear models were only approximately valid. After quantum mechanics, nature itself suddenly became linear. This had profound consequences for mathematics. During the nineteenth century Sophus Lie developed his elaborate theory of continuous groups, intended to clarify the behavior of classical dynamical systems. Lie groups were then of little interest either to mathematicians or to physicists. The nonlinear theory of Lie groups was too complicated for the mathematicians and too obscure for the physicists. Lie died a disappointed man. And then, fifty years later, it turned out that nature was precisely linear, and the theory of linear representations of Lie algebras was the natural language of particle physics. Lie groups and Lie algebras were reborn as one of the central themes of twentieth century mathematics.
在量子力学发明之前，经典物理始终是非线性的，线性模型只是近似有效。量子力学出现后，自然界本身突然变得线性了。这对数学产生了深远的影响。19世纪，索菲斯·李发展了他详尽的连续群理论，旨在阐明经典动力学系统的行为。但当时，李群既未引起数学家的多少兴趣，也未引起物理学家的多少关注。李群的非线性理论对数学家来说过于复杂，对物理学家来说过于晦涩。李在失望中离世。然而，50年后，事实证明自然界是精确线性的，李代数的线性表示理论成为了粒子物理的自然语言。李群和李代数作为20世纪数学的核心主题之一得以重生。

A third joke of nature is the existence of quasicrystals. In the nineteenth century the study of crystals led to a complete enumeration of possible discrete symmetry groups in Euclidean space. Theorems were proved, establishing the fact that in three-dimensional space discrete symmetry groups could contain only rotations of order three, four, or six. Then in 1984 quasi-crystals were discovered, real solid objects growing out of liquid metal alloys, showing the symmetry of the icosahedral group, which includes five-fold rotations. Meanwhile, the mathematician Roger Penrose discovered the Penrose tilings of the plane. These are arrangements of parallelograms that cover a plane with pentagonal long-range order. The alloy quasi-crystals are three-dimensional analogs of the two-dimensional Penrose tilings. After these discoveries, mathematicians had to enlarge the theory of crystallographic groups to include quasicrystals. That is a major program of research which is still in progress.
第三个“自然的玩笑”是准晶体的存在。19世纪，对晶体的研究导致了欧几里得空间中可能的离散对称群的完整枚举。定理证明，在三维空间中，离散对称群只能包含3阶、4阶或6阶旋转。然而，1984年，准晶体被发现了，它们是从液态金属合金中生长出来的真实固体，具有二十面体群的对称性，其中包括五重旋转。与此同时，数学家罗杰·彭罗斯发现了平面上的彭罗斯镶嵌。这是一种由平行四边形组成的排列，以五边形的长程有序覆盖平面。合金准晶体是二维彭罗斯镶嵌的三维类似物。这些发现之后，数学家们不得不扩展晶体学群的理论，将准晶体包括进来。这是一项重大的研究计划，至今仍在进行中。

A fourth joke of nature is a similarity in behavior between quasi-crystals and the zeros of the Riemann Zeta function. The zeros of the zeta function are exciting to mathematicians because they are found to lie on a straight line and nobody understands why. The statement that with trivial exceptions they all lie on a straight line is the famous Riemann Hypothesis. To prove the Riemann Hypothesis has been the dream of young mathematicians for more than a hundred years. I am now making the outrageous suggestion that we might use quasi-crystals to prove the Riemann Hypothesis. Those of you who are mathematicians may consider the suggestion frivolous. Those who are not mathematicians may consider it uninteresting. Nevertheless I am putting it forward for your serious consideration. When the physicist Leo Szilard was young, he became dissatisfied with the ten commandments of Moses and wrote a new set of ten commandments to replace them. Szilard’s second commandment says: “Let your acts be directed towards a worthy goal, but do not ask if they can reach it: they are to be models and examples, not means to an end.” Szilard practiced what he preached. He was the first physicist to imagine nuclear weapons and the first to campaign actively against their use. His second commandment certainly applies here. The proof of the Riemann Hypothesis is a worthy goal, and it is not for us to ask whether we can reach it. I will give you some hints describing how it might be achieved. Here I will be giving voice to the mathematician that I was fifty years ago before I became a physicist. I will talk first about the Riemann Hypothesis and then about quasi-crystals.
第四个“自然的玩笑”是准晶体和黎曼zeta函数零点在行为上的相似性。zeta函数的零点让数学家们兴奋不已，因为它们被发现位于一条直线上，而没有人明白为什么。除了一些平凡的例外，所有零点都位于一条直线上，这一陈述就是著名的黎曼假设。一百多年来，证明黎曼假设一直是年轻数学家的梦想。我现在要提出一个大胆的建议：我们或许可以用准晶体来证明黎曼假设。你们当中的数学家可能会认为这个建议很轻率，非数学家可能会觉得它无趣。尽管如此，我还是希望你们认真考虑一下。物理学家利奥·西拉德年轻时，对摩西的十诫不满，于是写下了一套新的十诫来取而代之。西拉德的第二条诫命是：“让你的行为指向一个有价值的目标，但不要问是否能达到它：它们应该是榜样和范例，而不是达到目的的手段。”西拉德言行一致。他是第一个构想核武器的物理学家，也是第一个积极反对使用核武器的人。他的第二条诫命在这里无疑是适用的。证明黎曼假设是一个有价值的目标，我们不必问是否能实现它。我会给你们一些提示，说明如何可能实现这一目标。在这里，我将以五十年前还是数学家（后来成为物理学家）的身份来说话。我会先谈谈黎曼假设，然后再谈谈准晶体。

There were until recently two supreme unsolved problems in the world of pure mathematics, the proof of Fermat’s Last Theorem and the proof of the Riemann Hypothesis. Twelve years ago, my Princeton colleague Andrew Wiles polished off Fermat’s Last Theorem, and only the Riemann Hypothesis remains. Wiles’ proof of the Fermat Theorem was not just a technical stunt. It required the discovery and exploration of a new field of mathematical ideas, far wider and more consequential than the Fermat Theorem itself. It is likely that any proof of the Riemann Hypothesis will likewise lead to a deeper understanding of many diverse areas of mathematics and perhaps of physics too. Riemann’s zeta-function, and other zeta-functions similar to it, appear ubiquitously in number theory, in the theory of dynamical systems, in geometry, in function theory, and in physics. The zeta-function stands at a junction where paths lead in many directions. A proof of the hypothesis will illuminate all the connections. Like every serious student of pure mathematics, when I was young I had dreams of proving the Riemann Hypothesis. I had some vague ideas that I thought might lead to a proof. In recent years, after the discovery of quasi-crystals, my ideas became a little less vague. I offer them here for the consideration of any young mathematician who has ambitions to win a Fields Medal.
直到最近，纯数学界还有两个最高级别的未解决问题：费马大定理的证明和黎曼假设的证明。十二年前，我的普林斯顿同事安德鲁·怀尔斯解决了费马大定理，现在只剩下黎曼假设了。怀尔斯对费马大定理的证明不仅仅是一项技术壮举。它需要发现和探索一个新的数学思想领域，这个领域比费马大定理本身更广阔，影响也更深远。任何对黎曼假设的证明都可能同样带来对许多不同数学领域，或许还有物理学领域的更深刻理解。黎曼zeta函数以及其他类似的zeta函数，在数论、动力系统理论、几何学、函数论和物理学中都无处不在。zeta函数处于一个多条路径交汇的路口。对这一假设的证明将阐明所有的联系。像所有认真的纯数学学生一样，我年轻时也曾梦想证明黎曼假设。我有一些模糊的想法，认为可能会导向证明。近年来，在准晶体被发现后，我的想法变得不那么模糊了。我把这些想法提出来，供任何有志于获得菲尔兹奖的年轻数学家参考。

Quasi-crystals can exist in spaces of one, two, or three dimensions. From the point of view of physics, the three-dimensional quasi-crystals are the most interesting, since they inhabit our three-dimensional world and can be studied experimentally. From the point of view of a mathematician, one-dimensional quasi-crystals are much more interesting than two-dimensional or three- dimensional quasi-crystals because they exist in far greater variety. The mathematical definition of a quasi-crystal is as follows. A quasi-crystal is a distribution of discrete point masses whose Fourier transform is a distribution of discrete point frequencies. Or to say it more briefly, a quasi-crystal is a pure point distribution that has a pure point spectrum. This definition includes as a special case the ordinary crystals, which are periodic distributions with periodic spectra.
准晶体可以存在于一维、二维或三维空间中。从物理学的角度来看，三维准晶体最有趣，因为它们存在于我们的三维世界中，可以通过实验进行研究。从数学家的角度来看，一维准晶体比二维或三维准晶体有趣得多，因为它们的种类要多得多。准晶体的数学定义如下：准晶体是一种离散点质量分布，其傅里叶变换是离散点频率分布。或者更简而言之，准晶体是具有纯点谱的纯点分布。这个定义包括作为特例的普通晶体，它们是具有周期性谱的周期性分布。

Excluding the ordinary crystals, quasi-crystals in three dimensions come in very limited variety, all of them associated with the icosahedral group. The two-dimensional quasicrystals are more numerous, roughly one distinct type associated with each regular polygon in a plane. The two- dimensional quasi-crystal with pentagonal symmetry is the famous Penrose tiling of the plane. Finally, the one-dimensional quasi-crystals have a far richer structure since they are not tied to any rotational symmetries. So far as I know, no complete enumeration of one-dimensional quasi-crystals exists. It is known that a unique quasi-crystal exists corresponding to every Pisot- Vijayaraghavan number or PV number. A PV number is a real algebraic integer, a root of a polynomial equation with integer coefficients, such that all the other roots have absolute value less than one, [1]. The set of all PV numbers is infinite and has a remarkable topological structure. The set of all one-dimensional quasi-crystals has a structure at least as rich as the set of all PV numbers and probably much richer. We do not know for sure, but it is likely that a huge universe of one-dimensional quasi-crystals not associated with PV numbers is waiting to be discovered.
排除普通晶体，三维准晶体的种类非常有限，都与二十面体群相关。二维准晶体的种类更多，大致上与平面中的每个正多边形相关联的有一种独特类型。具有五边形对称性的二维准晶体是著名的平面彭罗斯镶嵌。最后，一维准晶体具有丰富得多的结构，因为它们不受任何旋转对称性的限制。据我所知，目前还没有对一维准晶体的完整枚举。已知每个皮索特-维贾亚拉加万数（PV数）都对应一个独特的准晶体。PV数是一个实代数整数，是一个整系数多项式方程的根，且所有其他根的绝对值都小于1[1]。所有PV数的集合是无限的，并且具有显著的拓扑结构。所有一维准晶体的集合，其结构至少与所有PV数的集合一样丰富，可能还要丰富得多。我们不能确定，但很可能存在大量与PV数无关的一维准晶体有待发现。

Here comes the connection of the one- dimensional quasi-crystals with the Riemann hypothesis. If the Riemann hypothesis is true, then the zeros of the zeta-function form a one- dimensional quasi-crystal according to the definition. They constitute a distribution of point masses on a straight line, and their Fourier transform is likewise a distribution of point masses, one at each of the logarithms of ordinary prime numbers and prime-power numbers. My friend Andrew Odlyzko has published a beautiful computer calculation of the Fourier transform of the zeta-function zeros, [6]. The calculation shows precisely the expected structure of the Fourier transform, with a sharp discontinuity at every logarithm of a prime or prime-power number and nowhere else.
接下来谈谈一维准晶体与黎曼假设的联系。如果黎曼假设成立，那么根据定义，zeta函数的零点构成一个一维准晶体。它们在一条直线上形成点质量分布，其傅里叶变换同样是点质量分布，每个点对应于普通素数和素数幂的对数。我的朋友安德鲁·奥德里兹科发表了一项关于zeta函数零点傅里叶变换的精彩计算机计算结果[6]。该计算精确地显示了预期的傅里叶变换结构，在每个素数或素数幂的对数处有明显的不连续性，而在其他地方则没有。

My suggestion is the following. Let us pretend that we do not know that the Riemann Hypothesis is true. Let us tackle the problem from the other end. Let us try to obtain a complete enumeration and classification of one-dimensional quasi- crystals. That is to say, we enumerate and classify all point distributions that have a discrete point spectrum. Collecting and classifying new species of objects is a quintessentially Baconian activity. It is an appropriate activity for mathematical frogs. We shall then find the well-known quasi-crystals associated with PV numbers, and also a whole universe of other quasi- crystals, known and unknown. Among the multitude of other quasi-crystals we search for one corresponding to the Riemann zeta-function and one corresponding to each of the other zeta-functions that resemble the Riemann zeta-function. Suppose that we find one of the quasi-crystals in our enumeration with properties that identify it with the zeros of the Riemann zeta-function. Then we have proved the Riemann Hypothesis and we can wait for the telephone call announcing the award of the Fields Medal.
我的建议如下：让我们假设不知道黎曼假设是正确的，从另一端着手解决这个问题。我们尝试对一维准晶体进行完整的枚举和分类，也就是说，枚举并分类所有具有离散点谱的点分布。收集和分类新的“物种”是典型的培根式活动，适合数学青蛙们参与。届时，我们会发现与PV数相关的已知准晶体，以及一整个由其他已知和未知准晶体组成的世界。在众多其他准晶体中，我们要寻找一个与黎曼zeta函数对应的准晶体，以及与其他类似黎曼zeta函数的每个zeta函数对应的准晶体。假设我们在枚举中发现某个准晶体，其性质与黎曼zeta函数的零点相吻合，那么我们就证明了黎曼假设，之后就可以等待宣布获得菲尔兹奖的电话了。

Abram Besicovitch
艾布拉姆·贝西科维奇

Hermann Weyl
赫尔曼·外尔

These are of course idle dreams. The problem of classifying one- dimensional quasi-crystals is horrendously difficult, probably at least as difficult as the problems that Andrew Wiles took seven years to explore. But if we take a Baconian point of view, the history of mathematics is a history of horrendously difficult problems being solved by young people too ignorant to know that they were impossible. The classification of quasi-crystals is a worthy goal, and might even turn out to be achievable. Problems of that degree of difficulty will not be solved by old men like me. I leave this problem as an exercise for the young frogs in the audience.
当然，这些都是不切实际的梦想。对一维准晶体进行分类的问题极其困难，其难度可能至少与安德鲁·怀尔斯花了七年时间研究的问题相当。但如果从培根式的观点来看，数学史就是一部极其困难的问题被年轻人解决的历史，这些年轻人懵懂无知，不知道这些问题是不可能解决的。准晶体的分类是一个有价值的目标，甚至可能是可以实现的。这种难度的问题不会由我这样的老人解决，我把这个问题留给听众中的年轻青蛙们作为练习。

Abram Besicovitch and Hermann Weyl

艾布拉姆·贝西科维奇与赫尔曼·外尔

Let me now introduce you to some notable frogs and birds that I knew personally. I came to Cambridge University as a student in 1941 and had the tremendous luck to be given the Russian mathematician Abram Samoilovich Besicovitch as my supervisor. Since this was in the middle of World War Two, there were very few students in Cambridge, and almost no graduate students. Although I was only seventeen years old and Besicovitch was already a famous professor, he gave me a great deal of his time and attention, and we became life-long friends. He set the style in which I began to work and think about mathematics. He gave wonderful lectures on measure-theory and integration, smiling amiably when we laughed at his glorious abuse of the English language. I remember only one occasion when he was annoyed by our laughter. He remained silent for a while and then said, “Gentlemen. Fifty million English speak English you speak. Hundred and fifty million Russians speak English I speak.”
现在我来介绍一些我亲自认识的著名青蛙和鸟。1941年，我作为学生来到剑桥大学，非常幸运地得到了俄罗斯数学家艾布拉姆·萨莫伊洛维奇·贝西科维奇的指导。由于当时正值二战中期，剑桥的学生寥寥无几，几乎没有研究生。尽管我只有17岁，而贝西科维奇已是著名教授，但他花了很多时间和精力指导我，我们成了终身好友。他奠定了我研究和思考数学的风格。他讲授的测度论和积分课程非常精彩，当我们因他对英语的绝妙误用而发笑时，他会和蔼地微笑。我只记得有一次他被我们的笑声惹恼了。他沉默了一会儿，然后说：“先生们，5000万英国人说你们说的英语，1.5亿俄罗斯人说我说的英语。”

Besicovitch was a frog, and he became famous when he was young by solving a problem in elementary plane geometry known as the Kakeya problem. The Kakeya problem was the following. A line segment of length one is allowed to move freely in a plane while rotating through an angle of 360 degrees. What is the smallest area of the plane that it can cover during its rotation? The problem was posed by the Japanese mathematician Kakeya in 1917 and remained a famous unsolved problem for ten years. George Birkhoff, the leading American mathematician at that time, publicly proclaimed that the Kakeya problem and the fourcolor problem were the outstanding unsolved problems of the day. It was widely believed that the minimum area was (\pi / 8), which is the area of a three-cusped hypocycloid. The three-cusped hypocycloid is a beautiful three-pointed curve. It is the curve traced out by a point on the circumference of a circle with radius one-quarter, when the circle rolls around the inside of a fixed circle with radius three-quarters. The line segment of length one can turn while always remaining tangent to the hypocycloid with its two ends also on the hypocycloid. This picture of the line turning while touching the inside of the hypocycloid at three points was so elegant that most people believed it must give the minimum area. Then Besicovitch surprised everyone by proving that the area covered by the line as it turns can be less than (\varepsilon) for any positive (\varepsilon).
贝西科维奇是一只青蛙，他年轻时因解决了一个被称为“挂谷问题”的初等平面几何问题而闻名。挂谷问题如下：一条长度为1的线段在平面内自由移动并旋转360度，它在旋转过程中所能覆盖的最小平面面积是多少？这个问题由日本数学家挂谷宗一于1917年提出，在十年内都是著名的未解决问题。当时美国顶尖数学家乔治·伯克霍夫公开宣称，挂谷问题和四色问题是当时突出的未解决问题。人们普遍认为，最小面积是(\pi / 8)，即三尖点内摆线的面积。三尖点内摆线是一种美丽的三尖曲线，当半径为1/4的圆在半径为3/4的固定圆内部滚动时，圆周长上一点所描绘出的曲线就是它。长度为1的线段在旋转时，始终与该内摆线相切，且两端也在该内摆线上。这种线段旋转时与内摆线内部三点接触的景象非常优雅，因此大多数人认为这一定能给出最小面积。然而，贝西科维奇证明，对于任意正数(\varepsilon)，线段旋转所覆盖的面积都可以小于(\varepsilon)，这让所有人都感到惊讶。

Besicovitch had actually solved the problem in 1920 before it became famous, not even knowing that Kakeya had proposed it. In 1920 he published the solution in Russian in the Journal of the Perm Physics and Mathematics Society, a journal that was not widely read. The university of Perm, a city 1,100 kilometers east of Moscow, was briefly a refuge for many distinguished mathematicians after the Russian revolution. They published two volumes of their journal before it died amid the chaos of revolution and civil war. Outside Russia the journal was not only unknown but unobtainable. Besicovitch left Russia in 1925 and arrived at Copenhagen, where he learned about the famous Kakeya problem that he had solved five years earlier. He published the solution again, this time in English in the Mathematische Zeitschrift. The Kakeya problem as Kakeya proposed it was a typical frog problem, a concrete problem without much connection with the rest of mathematics. Besicovitch gave it an elegant and deep solution, which revealed a connection with general theorems about the structure of sets of points in a plane.
实际上，贝西科维奇在1920年就解决了这个问题，当时该问题尚未出名，他甚至不知道挂谷宗一提出了这个问题。1920年，他用俄语在《彼尔姆物理数学学会杂志》上发表了解答，该杂志并不广为流传。彼尔姆市位于莫斯科以东1100公里处，俄国革命后，彼尔姆大学曾短暂地成为许多杰出数学家的避难所。他们出版了两卷杂志，之后该杂志就在革命和内战的混乱中停刊了。在俄罗斯之外，这份杂志不仅无人知晓，也难以获取。1925年，贝西科维奇离开俄罗斯，抵达哥本哈根，在那里他才得知自己五年前解决的问题就是著名的挂谷问题。他再次发表了这个解答，这次是用英语发表在《数学杂志》上。挂谷提出的挂谷问题是一个典型的青蛙式问题，是一个与数学其他部分没有太多联系的具体问题。贝西科维奇给出了优雅而深刻的解答，揭示了它与平面点集结构的一般定理之间的联系。

The Besicovitch style is seen at its finest in his three classic papers with the title, “On the fundamental geometric properties of linearly measurable plane sets of points”, published in Mathematische Annalen in the years 1928, 1938, and 1939. In these papers he proved that every linearly measurable set in the plane is divisible into a regular and an irregular component, that the regular component has a tangent almost everywhere, and the irregular component has a projection of measure zero onto almost all directions. Roughly speaking, the regular component looks like a collection of continuous curves, while the irregular component looks nothing like a continuous curve. The existence and the properties of the irregular component are connected with the Besicovitch solution of the Kakeya problem. One of the problems that he gave me to work on was the division of measurable sets into regular and irregular components in spaces of higher dimensions. I got nowhere with the problem, but became permanently imprinted with the Besicovitch style. The Besicovitch style is architectural. He builds out of simple elements a delicate and complicated architectural structure, usually with a hierarchical plan, and then, when the building is finished, the completed structure leads by simple arguments to an unexpected conclusion. Every Besicovitch proof is a work of art, as carefully constructed as a Bach fugue.
贝西科维奇的风格在他三篇经典论文中体现得淋漓尽致，论文标题为《论线性可测平面点集的基本几何性质》，分别于1928年、1938年和1939年发表在《数学年刊》上。在这些论文中，他证明了平面上的每个线性可测集都可以分为正则部分和非正则部分，正则部分几乎处处有切线，非正则部分在几乎所有方向上的投影测度为零。粗略地说，正则部分看起来像一系列连续曲线的集合，而非正则部分则完全不像连续曲线。非正则部分的存在及其性质与贝西科维奇对挂谷问题的解答有关。他让我研究的一个问题是，在高维空间中把可测集分为正则部分和非正则部分。我在这个问题上毫无进展，但却永远打上了贝西科维奇风格的烙印。贝西科维奇的风格颇具建筑感，他用简单的元素构建出精致而复杂的建筑结构，通常带有层次分明的规划，然后在建筑完成后，通过简单的论证从完整的结构中得出意想不到的结论。每一个贝西科维奇式的证明都是一件艺术品，如同巴赫的赋格曲一样精心构造。

A few years after my apprenticeship with Besicovitch, I came to Princeton and got to know Hermann Weyl. Weyl was a prototypical bird, just as Besicovitch was a prototypical frog. I was lucky to overlap with Weyl for one year at the Princeton Institute for Advanced Study before he retired from the Institute and moved back to his old home in Zürich. He liked me because during that year I published papers in the Annals of Mathematics about number theory and in the Physical Review about the quantum theory of radiation. He was one of the few people alive who was at home in both subjects. He welcomed me to the Institute, in the hope that I would be a bird like himself. He was disappointed. I remained obstinately a frog. Although I poked around in a variety of mud-holes, I always looked at them one at a time and did not look for connections between them. For me, number theory and quantum theory were separate worlds with separate beauties. I did not look at them as Weyl did, hoping to find clues to a grand design.
在贝西科维奇那里学习几年后，我来到普林斯顿，认识了赫尔曼·外尔。外尔是典型的鸟，就像贝西科维奇是典型的青蛙一样。在外尔从普林斯顿高等研究院退休并搬回苏黎世的老家之前，我很幸运地与他在研究院共事了一年。他喜欢我，因为那一年我在《数学年刊》上发表了关于数论的论文，在《物理评论》上发表了关于辐射量子理论的论文。他是当时少数对这两个领域都得心应手的人之一。他欢迎我来到研究院，希望我能成为像他一样的鸟。但他失望了，我固执地还是一只青蛙。尽管我在各种各样的泥坑里探索，但我总是一次只关注一个，不去寻找它们之间的联系。对我来说，数论和量子理论是两个独立的世界，各有其美。我没有像外尔那样，希望从中找到宏大设计的线索。

Weyl’s great contribution to the quantum theory of radiation was his invention of gauge fields. The idea of gauge fields had a curious history. Weyl invented them in 1918 as classical fields in his unified theory of general relativity and electromagnetism, [7]. He called them “gauge fields” because they were concerned with the non-integrability of measurements of length. His unified theory was promptly and publicly rejected by Einstein. After this thunderbolt from on high, Weyl did not abandon his theory but moved on to other things. The theory had no experimental consequences that could be tested. Then in 1929, after quantum mechanics had been invented by others, Weyl realized that his gauge fields fitted far better into the quantum world than they did into the classical world, [8]. All that he needed to do, to change a classical gauge into a quantum gauge, was to change real numbers into complex numbers. In quantum mechanics, every quantum of electric charge carries with it a complex wave function with a phase, and the gauge field is concerned with the non-integrability of measurements of phase. The gauge field could then be precisely identified with the electromagnetic potential, and the law of conservation of charge became a consequence of the local phase invariance of the theory.
外尔对辐射量子理论的重大贡献是他发明了规范场。规范场的概念有着奇特的历史。1918年，外尔在他的广义相对论和电磁学统一理论中，将规范场作为经典场引入[7]。他称之为“规范场”，是因为它们与长度测量的不可积性有关。他的统一理论很快就被爱因斯坦公开否定了。在这次来自权威的打击之后，外尔并没有放弃他的理论，而是转而研究其他东西。这个理论没有可检验的实验结果。后来在1929年，在其他人发明量子力学之后，外尔意识到他的规范场更适合量子世界，而非经典世界[8]。要将经典规范转变为量子规范，他所需做的就是把实数改为复数。在量子力学中，每个电荷量子都带有一个具有相位的复波函数，而规范场与相位测量的不可积性有关。这样，规范场就可以精确地等同于电磁势，电荷守恒定律也成为该理论局域相位不变性的一个结果。

Weyl died four years after he returned from Princeton to Zürich, and I wrote his obituary for the journal Nature, [3]. “Among all the mathematicians who began their working lives in the twentieth century,” I wrote, “Hermann Weyl was the one who made major contributions in the greatest number of different fields. He alone could stand comparison with the last great universal mathematicians of the nineteenth century, Hilbert and Poincaré. So long as he was alive, he embodied a living contact between the main lines of advance in pure mathematics and in theoretical physics. Now he is dead, the contact is broken, and our hopes of comprehending the physical universe by a direct use of creative mathematical imagination are for the time being ended.” I mourned his passing, but I had no desire to pursue his dream. I was happy to see pure mathematics and physics marching ahead in opposite directions.
外尔从普林斯顿回到苏黎世四年后去世，我为《自然》杂志撰写了他的讣告[3]。我在讣告中写道：“在所有于20世纪开始职业生涯的数学家中，赫尔曼·外尔是在最多不同领域做出重大贡献的人。只有他能与19世纪最后几位伟大的全能数学家——希尔伯特和庞加莱相提并论。只要他还在世，他就代表着纯数学和理论物理学主要发展路线之间的活生生的联系。现在他去世了，这种联系中断了，我们通过直接运用创造性的数学想象力来理解物理宇宙的希望暂时破灭了。”我为他的逝世哀悼，但我没有意愿去追寻他的梦想。我乐于看到纯数学和物理学朝着相反的方向前进。

The obituary ended with a sketch of Weyl as a human being: “Characteristic of Weyl was an aesthetic sense which dominated his thinking on all subjects. He once said to me, half joking, ‘My work always tried to unite the true with the beautiful; but when I had to choose one or the other, I usually chose the beautiful’. This remark sums up his personality perfectly. It shows his profound faith in an ultimate harmony of Nature, in which the laws should inevitably express themselves in a mathematically beautiful form. It shows also his recognition of human frailty, and his humor, which always stopped him short of being pompous. His friends in Princeton will remember him as he was when I last saw him, at the Spring Dance of the Institute for Advanced Study last April: a big jovial man, enjoying himself splendidly, his cheerful frame and his light step giving no hint of his sixty-nine years.”
讣告最后描绘了外尔的为人：“外尔的特点是一种审美感，这种审美感主导了他对所有问题的思考。他曾半开玩笑地对我说：‘我的工作总是试图将真实与美丽结合起来；但当我必须在两者之间选择时，我通常会选择美丽。’这句话完美地概括了他的个性。它表明了他对自然最终和谐的深刻信念，在这种和谐中，规律必然会以数学上美丽的形式表现出来。它也表明了他对人类弱点的认识，以及他的幽默感，这种幽默感使他从不显得浮夸。普林斯顿的朋友们会记得他最后在我眼中的样子，那是去年四月在高等研究院的春季舞会上：一个身材高大、性格开朗的人，尽情享受着快乐，他欢快的身形和轻快的步伐丝毫没有显露出他已69岁高龄。”

The fifty years after Weyl’s death were a golden age of experimental physics and observational astronomy, a golden age for Baconian travelers picking up facts, for frogs exploring small patches of the swamp in which we live. During these fifty years, the frogs accumulated a detailed knowledge of a large variety of cosmic structures and a large variety of particles and interactions. As the exploration of new territories continued, the universe became more complicated. Instead of a grand design displaying the simplicity and beauty of Weyl’s mathematics, the explorers found weird objects such as quarks and gamma-ray bursts, weird concepts such as supersymmetry and multiple universes. Meanwhile, mathematics was also becoming more complicated, as exploration continued into the phenomena of chaos and many other new areas opened by electronic computers. The mathematicians discovered the central mystery of computability, the conjecture represented by the statement P is not equal to NP. The conjecture asserts that there exist mathematical problems which can be quickly solved in individual cases but cannot be solved by a quick algorithm applicable to all cases. The most famous example of such a problem is the traveling salesman problem, which is to find the shortest route for a salesman visiting a set of cities, knowing the distance between each pair. All the experts believe that the conjecture is true, and that the traveling salesman problem is an example of a problem that is P but not NP. But nobody has even a glimmer of an idea how to prove it. This is a mystery that could not even have been formulated within the nineteenth-century mathematical universe of Hermann Weyl.
外尔去世后的五十年是实验物理学和观测天文学的黄金时代，是培根式的探索者收集事实、青蛙探索我们所生活的沼泽中小块区域的黄金时代。在这五十年里，青蛙们积累了关于各种各样宇宙结构以及各种各样粒子和相互作用的详细知识。随着对新领域探索的继续，宇宙变得更加复杂。探索者们没有发现展现外尔数学中那种简洁和美丽的宏大设计，而是发现了诸如夸克和伽马射线暴等奇特物体，以及超对称性和多重宇宙等奇特概念。与此同时，随着对混沌现象以及电子计算机开辟的许多其他新领域的探索不断深入，数学也变得越来越复杂。数学家们发现了可计算性的核心谜团，即“P不等于NP”的猜想。该猜想断言，存在一些数学问题，在个别情况下可以快速解决，但却无法通过适用于所有情况的快速算法来解决。这类问题最著名的例子是旅行商问题，即已知每个城市之间的距离，为一个要访问多个城市的推销员找到最短路线。所有专家都认为这个猜想是正确的，并且旅行商问题就是一个属于P问题而非NP问题的例子。但没有人对如何证明这一点有丝毫头绪。这是一个在赫尔曼·外尔所处的19世纪数学世界中甚至无法提出的谜团。

Chen Ning (Frank) Yang
杨振宁

Yuri Manin
尤里·马宁

Frank Yang and Yuri Manin

杨振宁与尤里·马宁

The last fifty years have been a hard time for birds. Even in hard times, there is work for birds to do, and birds have appeared with the courage to tackle it. Soon after Weyl left Princeton, Frank Yang arrived from Chicago and moved into Weyl’s old house. Yang took Weyl’s place as the leading bird among my generation of physicists. While Weyl was still alive, Yang and his student Robert Mills discovered the Yang-Mills theory of non-Abelian gauge fields, a marvelously elegant extension of Weyl’s idea of a gauge field, [11]. Weyl’s gauge field was a classical quantity, satisfying the commutative law of multiplication. The Yang-Mills theory had a triplet of gauge fields which did not commute. They satisfied the commutation rules of the three components of a quantum mechanical spin,which are generators of the simplest non-Abelian Lie algebra (A_{2}). The theory was later generalized so that the gauge fields could be generators of any finite-dimensional Lie algebra. With this generalization, the Yang-Mills gauge field theory provided the framework for a model of all the known particles and interactions, a model that is now known as the Standard Model of particle physics. Yang put the finishing touch to it by showing that Einstein’s theory of gravitation fits into the same framework, with the Christoffel three-index symbol taking the role of gauge field, [10].
过去五十年对鸟来说是艰难的时期。即使在艰难时期，鸟也有工作要做，而且已经有鸟有勇气去应对。外尔离开普林斯顿后不久，杨振宁从芝加哥来到这里，住进了外尔的旧居。在我这一代物理学家中，杨振宁接替外尔成为了主要的鸟。在外尔还在世时，杨振宁和他的学生罗伯特·米尔斯就发现了非阿贝尔规范场的杨-米尔斯理论，这是对外尔规范场思想的极其优雅的扩展[11]。外尔的规范场是经典量，满足乘法交换律。杨-米尔斯理论中有三个不交换的规范场，它们满足量子力学自旋三个分量的对易规则，0 0o {2})的生成元。该理论后来得到推广，使得规范场可以是任何有限维李代数的生成元。通过这种推广，杨-米尔斯规范场理论为所有已知粒子和相互作用的模型提供了框架，这个模型现在被称为粒子物理学的标准模型。杨振宁通过证明爱因斯坦的引力理论也符合这个框架，为该理论画上了圆满的句号，其中克里斯托费尔三指标符号扮演着规范场的角色[10]。

In an appendix to his 1918 paper, added in 1955 for the volume of selected papers published to celebrate his seventieth birthday, Weyl expressed his final thoughts about gauge field theories (my translation), [12]: “The strongest argument for my theory seemed to be this, that gauge invariance was related to conservation of electric charge in the same way as coordinate invariance was related to conservation of energy and momentum.” Thirty years later Yang was in Zürich for the celebration of Weyl’s hundredth birthday. In his speech, [12], Yang quoted this remark as evidence of Weyl’s devotion to the idea of gauge invariance as a unifying principle for physics. Yang then went on, “Symmetry, Lie groups, and gauge invariance are now recognized, through theoretical and experimental developments, to play essential roles in determining the basic forces of the physical universe. I have called this the principle that symmetry dictates interaction.” This idea, that symmetry dictates interaction, is Yang’s generalization of Weyl’s remark. Weyl observed that gauge invariance is intimately connected with physical conservation laws. Weyl could not go further than this, because he knew only the gauge invariance of commuting Abelian fields. Yang made the connection much stronger by introducing non-Abelian gauge fields. With non-Abelian gauge fields generating nontrivial Lie algebras, the possible forms of interaction between fields become unique, so that symmetry dictates interaction. This idea is Yang’s greatest contribution to physics. It is the contribution of a bird, flying high over the rain forest of little problems in which most of us spend our lives.
在1918年论文的附录中（该附录是1955年为庆祝他七十岁生日而出版的论文选集所添加的），外尔表达了他对规范场理论的最终想法（我的翻译）[12]：“我的理论最有力的论据似乎是，规范不变性与电荷守恒的关系，如同坐标不变性与能量和动量守恒的关系。”三十年后，杨振宁在苏黎世参加外尔百年诞辰庆典。在他的演讲中[12]，杨振宁引用了这句话，作为外尔致力于将规范不变性作为物理学统一原理的证据。杨振宁接着说：“通过理论和实验的发展，对称性、李群和规范不变性现在被认为在决定物理宇宙的基本力方面起着重要作用。我将此称为‘对称性决定相互作用’原理。”这种“对称性决定相互作用”的思想，是杨振宁对外尔言论的推广。外尔观察到规范不变性与物理守恒定律密切相关。但外尔只能做到这一步，因为他只知道可交换的阿贝尔场的规范不变性。杨振宁通过引入非阿贝尔规范场，使这种联系更加紧密。由于非阿贝尔规范场生成非平凡的李代数，场之间可能的相互作用形式变得唯一，因此对称性决定相互作用。这个思想是杨振宁对物理学的最大贡献，这是一只鸟的贡献，它翱翔在我们大多数人所沉迷的众多小问题构成的雨林之上。

Another bird for whom I have a deep respect is the Russian mathematician Yuri Manin, who recently published a delightful book of essays with the title Mathematics as Metaphor [5]. The book was published in Moscow in Russian, and by the American Mathematical Society in English. I wrote a preface for the English version, and I give you here a short quote from my preface. “Mathematics as Metaphor is a good slogan for birds. It means that the deepest concepts in mathematics are those which link one world of ideas with another. In the seventeenth century Descartes linked the disparate worlds of algebra and geometry with his concept of coordinates, and Newton linked the worlds of geometry and dynamics with his concept of fluxions, nowadays called calculus. In the nineteenth century Boole linked the worlds of logic and algebra with his concept of symbolic logic, and Riemann linked the worlds of geometry and analysis with his concept of Riemann surfaces. Coordinates, fluxions, symbolic logic, and Riemann surfaces are all metaphors, extending the meanings of words from familiar to unfamiliar contexts. Manin sees the future of mathematics as an exploration of metaphors that are already visible but not yet understood. The deepest such metaphor is the similarity in structure between number theory and physics. In both fields he sees tantalizing glimpses of parallel concepts, symmetries linking the continuous with the discrete. He looks forward to a unification which he calls the quantization of mathematics.
另一位我深怀敬意的鸟是俄罗斯数学家尤里·马宁，他最近出版了一本有趣的散文集，书名是《作为隐喻的数学》[5]。这本书在莫斯科以俄语出版，美国数学会出版了英文版。我为英文版写了序言，这里我引用序言中的一小段话：“‘数学作为隐喻’是鸟的一个好口号。它意味着数学中最深刻的概念是那些将一个思想世界与另一个思想世界联系起来的概念。17世纪，笛卡尔用坐标的概念将代数和几何这两个不同的世界联系起来；牛顿用流数（现在称为微积分）的概念将几何和动力学的世界联系起来。19世纪，布尔用符号逻辑的概念将逻辑和代数的世界联系起来；黎曼用黎曼曲面的概念将几何和分析的世界联系起来。坐标、流数、符号逻辑和黎曼曲面都是隐喻，将词语的含义从熟悉的语境扩展到不熟悉的语境。马宁将数学的未来视为对已显现但尚未被理解的隐喻的探索。其中最深刻的隐喻是数论和物理学之间的结构相似性。在这两个领域，他都看到了平行概念的诱人迹象，以及连接连续与离散的对称性。他期待着一种统一，他称之为数学的量子化。

“Manin disagrees with the Baconian story, that Hilbert set the agenda for the mathematics of the twentieth century when he presented his famous list of twenty-three unsolved problems to the International Congress of Mathematicians in Paris in 1900. According to Manin, Hilbert’s problems were a distraction from the central themes of mathematics. Manin sees the important advances in mathematics coming from programs, not from problems. Problems are usually solved by applying old ideas in new ways. Programs of research are the nurseries where new ideas are born. He sees the Bourbaki program, rewriting the whole of mathematics in a more abstract language, as the source of many of the new ideas of the twentieth century. He sees the Langlands program, unifying number theory with geometry, as a promising source of new ideas for the twenty-first. People who solve famous unsolved problems may win big prizes, but people who start new programs are the real pioneers.”
“马宁不同意培根式的说法，即希尔伯特1900年在巴黎国际数学家大会上提出著名的23个未解决问题时，为20世纪的数学设定了议程。马宁认为，希尔伯特的问题分散了人们对数学核心主题的注意力。马宁认为，数学的重要进展来自于纲领，而不是问题。问题通常是通过以新的方式应用旧思想来解决的。研究纲领是新思想诞生的温床。他认为，布尔巴基纲领用更抽象的语言重写整个数学，是20世纪许多新思想的来源。他认为，将数论与几何统一起来的朗兰兹纲领，是21世纪新思想的一个有希望的来源。解决著名未解决问题的人可能会赢得大奖，但开创新项目的人才是真正的先驱。”

The Russian version of Mathematics as Metaphor contains ten chapters that were omitted from the English version. The American Mathematical Society decided that these chapters would not be of interest to English language readers. The omissions are doubly unfortunate. First, readers of the English version see only a truncated view of Manin, who is perhaps unique among mathematicians in his broad range of interests extending far beyond mathematics. Second, we see a truncated view of Russian culture, which is less compartmentalized than English language culture, and brings mathematicians into closer contact with historians and artists and poets.
《作为隐喻的数学》的俄文版包含十个章节，这些章节在英文版中被删减了。美国数学会认为这些章节不会引起英语读者的兴趣。这种删减是双重不幸的。首先，英文版的读者只能看到一个不完整的马宁，在数学家中，他广泛的兴趣远超数学领域，这或许是独一无二的。其次，我们看到的俄罗斯文化也是不完整的，俄罗斯文化不像英语文化那样划分细密，它使数学家与历史学家、艺术家和诗人有着更密切的联系。

John von Neumann

约翰·冯·诺依曼

Another important figure in twentieth century mathematics was John von Neumann. Von Neumann was a frog, applying his prodigious technical skill to solve problems in many branches of mathematics and physics. He began with the foundations of mathematics. He found the first satisfactory set of axioms for set-theory, avoiding the logical paradoxes that Cantor had encountered in his attempts to deal with infinite sets and infinite numbers. Von Neumann’s axioms were used by his bird friend Kurt Gödel a few years later to prove the existence of undecidable propositions in mathematics. Gödel’s theorems gave birds a new vision of mathematics. After Gödel, mathematics was no longer a single structure tied together with a unique concept of truth, but an archipelago of structures with diverse sets of axioms and diverse notions of truth. Gödel showed that mathematics is inexhaustible. No matter which set of axioms is chosen as the foundation, birds can always find questions that those axioms cannot answer.
20世纪数学界另一位重要人物是约翰·冯·诺依曼。冯·诺依曼是一只青蛙，他运用自己非凡的技术能力解决了数学和物理学许多分支中的问题。他从数学基础开始研究。他为集合论找到了第一套令人满意的公理，避免了康托尔在尝试处理无穷集合和无穷数时遇到的逻辑悖论。几年后，他的鸟朋友库尔特·哥德尔利用冯·诺依曼的公理证明了数学中存在不可判定命题。哥德尔定理给了鸟们一种新的数学视野。哥德尔之后，数学不再是一个由独特真理概念维系的单一结构，而是一个由具有不同公理集和不同真理概念的结构组成的群岛。哥德尔表明，数学是无穷无尽的。无论选择哪一套公理作为基础，鸟们总能找到那些公理无法回答的问题。

Von Neumann went on from the foundations of mathematics to the foundations of quantum mechanics. To give quantum mechanics a firm mathematical foundation, he created a magnificent theory of rings of operators. Every observable quantity is represented by a linear operator, and the peculiarities of quantum behavior are faithfully represented by the algebra of operators. Just as Newton invented calculus to describe classical dynamics, von Neumann invented rings of operators to describe quantum dynamics.
冯·诺依曼从数学基础转向量子力学基础。为了给量子力学奠定坚实的数学基础，他创立了宏伟的算子环理论。每个可观测量都由一个线性算子表示，量子行为的特性由算子代数忠实地表示。正如牛顿发明微积分来描述经典动力学一样，冯·诺依曼发明算子环来描述量子动力学。

Von Neumann made fundamental contributions to several other fields, especially to game theory and to the design of digital computers. For the last ten years of his life, he was deeply involved with computers. He was so strongly interested in computers that he decided not only to study their design but to build one with real hardware and software and use it for doing science. I have vivid memories of the early days of von Neumann’s computer project at the Institute for Advanced Study in Princeton. At that time he had two main scientific interests, hydrogen bombs and meteorology. He used his computer during the night for doing hydrogen bomb calculations and during the day for meteorology. Most of the people hanging around the computer building in daytime were meteorologists. Their leader was Jule Charney. Charney was a real meteorologist, properly humble in dealing with the inscrutable mysteries of the weather, and skeptical of the ability of the computer to solve the mysteries. John von Neumann was less humble and less skeptical. I heard von Neumann give a lecture about the aims of his project. He spoke, as he always did, with great confidence. He said, “The computer will enable us to divide the atmosphere at any moment into stable regions and unstable regions. Stable regions we can predict. Unstable regions we can control.” Von Neumann believed that any unstable region could be pushed by a judiciously applied small perturbation so that it would move in any desired direction. The small perturbation would be applied by a fleet of airplanes carrying smoke generators, to absorb sunlight and raise or lower temperatures at places where the perturbation would be most effective. In particular, we could stop an incipient hurricane by identifying the position of an instability early enough, and then cooling that patch of air before it started to rise and form a vortex. Von Neumann, speaking in 1950, said it would take only ten years to build computers powerful enough to diagnose accurately the stable and unstable regions of the atmosphere. Then, once we had accurate diagnosis, it would take only a short time for us to have control. He expected that practical control of the weather would be a routine operation within the decade of the 1960s.
冯·诺依曼还在其他几个领域做出了基础性贡献，特别是在博弈论和数字计算机设计方面。在他生命的最后十年里，他全身心投入到计算机研究中。他对计算机的兴趣如此浓厚，以至于他不仅决定研究计算机的设计，还决定用真正的硬件和软件制造一台计算机，并将其用于科学研究。我对冯·诺依曼在普林斯顿高等研究院开展计算机项目的早期岁月有着清晰的记忆。当时他有两个主要的科学兴趣：氢弹和气象学。他晚上用计算机进行氢弹计算，白天用它研究气象学。白天在计算机大楼周围转悠的大多是气象学家，他们的领头人是朱尔·查尼。查尼是一位真正的气象学家，在处理神秘莫测的天气时态度谦逊，对计算机解决这些奥秘的能力持怀疑态度。约翰·冯·诺依曼则不那么谦逊，也不那么怀疑。我听过冯·诺依曼关于他项目目标的演讲，他像往常一样，充满信心地说：“计算机将使我们能够在任何时刻把大气分为稳定区域和不稳定区域。稳定区域我们可以预测，不稳定区域我们可以控制。”冯·诺依曼认为，通过审慎地施加小的扰动，可以推动任何不稳定区域向任何期望的方向发展。这种小扰动将由一队携带烟雾发生器的飞机施加，这些烟雾发生器吸收阳光，在扰动效果最佳的地方升高或降低温度。特别是，我们可以通过尽早确定不稳定区域的位置，在其开始上升并形成漩涡之前冷却该区域的空气，从而阻止飓风的形成。冯·诺依曼在1950年说，只需十年时间就能制造出足够强大的计算机，准确诊断大气的稳定和不稳定区域。然后，一旦我们有了准确的诊断，用不了多久就能实现控制。他预计，到20世纪60年代，实际控制天气将成为一项常规操作。

John von Neumann
约翰·冯·诺依曼

Mary Cartwright
玛丽·卡特赖特

Von Neumann, of course, was wrong. He was wrong because he did not know about chaos. We now know that when the motion of the atmosphere is locally unstable, it is very often chaotic. The word “chaotic” means that motions that start close together diverge exponentially from each other as time goes on. When the motion is chaotic, it is unpredictable, and a small perturbation does not move it into a stable motion that can be predicted. A small perturbation will usually move it into another chaotic motion that is equally unpredictable. So von Neumann’s strategy for controlling the weather fails. He was, after all, a great mathematician but a mediocre meteorologist.
当然，冯·诺依曼错了。他错了是因为他不知道混沌现象。我们现在知道，当大气运动局部不稳定时，往往是混沌的。“混沌”一词意味着，开始时非常接近的运动随着时间的推移会指数级地相互偏离。当运动是混沌的时，它是不可预测的，小的扰动不会使其进入可预测的稳定运动状态。小的扰动通常会使其进入另一种同样不可预测的混沌运动状态。因此，冯·诺依曼控制天气的策略失败了。毕竟，他是一位伟大的数学家，但却是一位平庸的气象学家。

Edward Lorenz discovered in 1963 that the solutions of the equations of meteorology are often chaotic. That was six years after von Neumann died. Lorenz was a meteorologist and is generally regarded as the discoverer of chaos. He discovered the phenomena of chaos in the meteorological context and gave them their modern names. But in fact I had heard the mathematician Mary Cartwright, who died in 1998 at the age of 97, describe the same phenomena in a lecture in Cambridge in 1943, twenty years before Lorenz discovered them. She called the phenomena by different names, but they were the same phenomena. She discovered them in the solutions of the van der Pol equation which describe the oscillations of a nonlinear amplifier, [2]. The van der Pol equation was important in World War II because nonlinear amplifiers fed power to the transmitters in early radar systems. The transmitters behaved erratically, and the Air Force blamed the manufacturers for making defective amplifiers. Mary Cartwright was asked to look into the problem. She showed that the manufacturers were not to blame. She showed that the van der Pol equation was to blame. The solutions of the van der Pol equation have precisely the chaotic behavior that the Air Force was complaining about. I heard all about chaos from Mary Cartwright seven years before I heard von Neumann talk about weather control, but I was not far-sighted enough to make the connection. It never entered my head that the erratic behavior of the van der Pol equation might have something to do with meteorology. If I had been a bird rather than a frog, I would probably have seen the connection, and I might have saved von Neumann a lot of trouble. If he had known about chaos in 1950, he would probably have thought about it deeply, and he would have had something important to say about it in 1954.
爱德华·洛伦兹在1963年发现，气象方程的解往往是混沌的。那是冯·诺依曼去世六年后。洛伦兹是一位气象学家，通常被认为是混沌现象的发现者。他在气象学背景下发现了混沌现象，并赋予它们现代名称。但事实上，我曾听过数学家玛丽·卡特赖特（她于1998年去世，享年97岁）在1943年剑桥的一次讲座中描述过同样的现象，这比洛伦兹发现它们早了二十年。她用不同的名称称呼这些现象，但它们本质上是相同的。她在描述非线性放大器振荡的范德波尔方程的解中发现了这些现象[2]。范德波尔方程在二战中很重要，因为非线性放大器为早期雷达系统的发射机供电。发射机的行为不稳定，空军指责制造商生产了有缺陷的放大器。玛丽·卡特赖特被请来调查这个问题。她表明，责任不在制造商，而在范德波尔方程。范德波尔方程的解恰好具有空军所抱怨的混沌行为。我在听冯·诺依曼谈论天气控制的七年前，就从玛丽·卡特赖特那里听说了关于混沌的一切，但我缺乏远见，没有把两者联系起来。我从未想过范德波尔方程的不稳定行为可能与气象学有关。如果我是一只鸟而不是青蛙，我可能会看到这种联系，或许能帮冯·诺依曼省去很多麻烦。如果他在1950年就知道混沌现象，他可能会深入思考，并且在1954年可能会就混沌现象发表一些重要的见解。

Von Neumann got into trouble at the end of his life because he was really a frog but everyone expected him to fly like a bird. In 1954 there was an International Congress of Mathematicians in Amsterdam. These congresses happen only once in four years and it is a great honor to be invited to speak at the opening session. The organizers of the Amsterdam congress invited von Neumann to give the keynote speech, expecting him to repeat the act that Hilbert had performed in Paris in 1900. Just as Hilbert had provided a list of unsolved problems to guide the development of mathematics for the first half of the twentieth century, von Neumann was invited to do the same for the second half of the century. The title of von Neumann’s talk was announced in the program of the congress. It was “Unsolved Problems in Mathematics: Address by Invitation of the Organizing Committee”. After the congress was over, the complete proceedings were published, with the texts of all the lectures except this one. In the proceedings there is a blank page with von Neumann’s name and the title of his talk. Underneath, it says, “No manuscript of this lecture was available.”
冯·诺依曼在晚年陷入了麻烦，因为他实际上是一只青蛙，但所有人都期望他像鸟一样翱翔。1954年，阿姆斯特丹举行了国际数学家大会。这种大会每四年举行一次，受邀在开幕式上发言是一项巨大的荣誉。阿姆斯特丹大会的组织者邀请冯·诺依曼发表主题演讲，期望他重现希尔伯特1900年在巴黎所做的事情。正如希尔伯特提出了一系列未解决问题，为20世纪上半叶的数学发展指明方向一样，人们邀请冯·诺依曼为20世纪下半叶做同样的事情。冯·诺依曼演讲的标题在大会日程中公布，是《数学中的未解决问题：应组织委员会邀请的演讲》。大会结束后，完整的会议记录出版了，其中包含了所有演讲的文本，唯独缺少这一篇。在会议记录中，有一页空白页，上面写着冯·诺依曼的名字和他的演讲标题，下面写着：“没有可用的演讲稿。”

What happened? I know what happened, because I was there in the audience, at 3:00 p.m. on Thursday, September 2, 1954, in the Concertgebouw concert hall. The hall was packed with mathematicians, all expecting to hear a brilliant lecture worthy of such a historic occasion. The lecture was a huge disappointment. Von Neumann had probably agreed several years earlier to give a lecture about unsolved problems and had then forgotten about it. Being busy with many other things, he had neglected to prepare the lecture. Then, at the last moment, when he remembered that he had to travel to Amsterdam and say something about mathematics, he pulled an old lecture from the 1930s out of a drawer and dusted it off. The lecture was about rings of operators, a subject that was new and fashionable in the 1930s. Nothing about unsolved problems. Nothing about the future. Nothing about computers, the subject that we knew was dearest to von Neumann’s heart. He might at least have had something new and exciting to say about computers. The audience in the concert hall became restless. Somebody said in a voice loud enough to be heard all over the hall, “Aufgewärmte Suppe”, which is German for “warmed-up soup”. In 1954 the great majority of mathematicians knew enough German to understand the joke. Von Neumann, deeply embarrassed, brought his lecture to a quick end and left the hall without waiting for questions.
发生了什么事？我知道发生了什么，因为1954年9月2日星期四下午3点，我就在阿姆斯特丹音乐厅的听众席上。大厅里坐满了数学家，所有人都期待着听到一场配得上这一历史性时刻的精彩演讲。但这场演讲却让人大失所望。冯·诺依曼可能在几年前就同意做一场关于未解决问题的演讲，后来却忘了这件事。由于忙于其他许多事情，他没有准备演讲。然后，在最后一刻，当他记起必须去阿姆斯特丹讲一些关于数学的内容时，他从抽屉里翻出了一篇20世纪30年代的旧演讲稿，稍作修改就用了。这篇演讲是关于算子环的，这个主题在20世纪30年代是新颖且流行的。演讲中没有提到未解决的问题，没有提到未来，也没有提到计算机——我们知道这是冯·诺依曼最心爱的主题。他至少可以说一些关于计算机的新奇有趣的内容。音乐厅里的听众变得不安起来。有人大声说出了一句德语“Aufgewärmte Suppe”，意思是“热过的汤”（指陈词滥调）。1954年，绝大多数数学家都懂 enough 德语，能明白这个笑话的意思。冯·诺依曼深感尴尬，匆匆结束了演讲，没等提问就离开了大厅。

Weak Chaos

弱混沌

If von Neumann had known about chaos when he spoke in Amsterdam, one of the unsolved problems that he might have talked about was weak chaos. The problem of weak chaos is still unsolved fifty years later. The problem is to understand why chaotic motions often remain bounded and do not cause any violent instability. A good example of weak chaos is the orbital motions of the planets and satellites in the solar system. It was discovered only recently that these motions are chaotic. This was a surprising discovery, upsetting the traditional picture of the solar system as the prime example of orderly stable motion. The mathematician Laplace two hundred years ago thought he had proved that the solar system is stable. It now turns out that Laplace was wrong. Accurate numerical integrations of the orbits show clearly that neighboring orbits diverge exponentially. It seems that chaos is almost universal in the world of classical dynamics.
如果冯·诺依曼在阿姆斯特丹演讲时就知道混沌现象，他可能会谈到的一个未解决问题就是弱混沌。五十年后，弱混沌问题仍然没有解决。这个问题是要理解为什么混沌运动往往保持有界，不会造成任何剧烈的不稳定性。弱混沌的一个很好的例子是太阳系中行星和卫星的轨道运动。直到最近才发现这些运动是混沌的。这是一个令人惊讶的发现，打破了将太阳系视为有序稳定运动典范的传统观念。两百年前，数学家拉普拉斯认为他证明了太阳系是稳定的。现在看来，拉普拉斯错了。精确的轨道数值积分清楚地表明，相邻轨道呈指数级偏离。在经典动力学世界中，混沌似乎几乎是普遍存在的。

Chaotic behavior was never suspected in the solar system before accurate long-term integrations were done, because the chaos is weak. Weak chaos means that neighboring trajectories diverge exponentially but never diverge far. The divergence begins with exponential growth but afterwards remains bounded. Because the chaos of the planetary motions is weak, the solar system can survive for four billion years. Although the motions are chaotic, the planets never wander far from their customary places, and the system as a whole does not fly apart. In spite of the prevalence of chaos, the Laplacian view of the solar system as a perfect piece of clockwork is not far from the truth.
在进行精确的长期积分之前，人们从未怀疑过太阳系中存在混沌行为，因为这种混沌是弱的。弱混沌意味着相邻轨迹呈指数级偏离，但从未偏离很远。偏离开始时呈指数增长，但随后保持有界。由于行星运动的混沌是弱的，太阳系才能存在四十亿年。尽管运动是混沌的，但行星从未远离它们通常的位置，整个系统也没有分崩离析。尽管混沌普遍存在，但拉普拉斯将太阳系视为完美钟表装置的观点也并非完全错误。

We see the same phenomena of weak chaos in the domain of meteorology. Although the weather in New Jersey is painfully chaotic, the chaos has firm limits. Summers and winters are unpredictably mild or severe, but we can reliably predict that the temperature will never rise to 45 degrees Celsius or fall to minus 30, extremes that are often exceeded in India or in Minnesota. There is no conservation law of physics that forbids temperatures from rising as high in New Jersey as in India, or from falling as low in New Jersey as in Minnesota. The weakness of chaos has been essential to the long-term survival of life on this planet. Weak chaos gives us a challenging variety of weather while protecting us from fluctuations so severe as to endanger our existence. Chaos remains mercifully weak for reasons that we do not understand. That is another unsolved problem for young frogs in the audience to take home. I challenge you to understand the reasons why the chaos observed in a great diversity of dynamical systems is generally weak.
在气象学领域，我们也能看到同样的弱混沌现象。尽管新泽西州的天气混乱得令人头疼，但这种混乱有明确的限度。夏季和冬季的气候是温和还是严酷难以预测，但我们可以可靠地预测，气温永远不会上升到45摄氏度，也不会下降到零下30摄氏度，而这样的极端气温在印度或明尼苏达州却很常见。物理学中没有守恒定律禁止新泽西州的气温上升到印度那么高，或者下降到明尼苏达州那么低。混沌的弱性对地球上生命的长期生存至关重要。弱混沌给我们带来了多变的天气挑战，同时保护我们免受足以危及生存的剧烈波动的影响。混沌幸好是弱的，其原因我们尚不清楚。这是另一个留给听众中的年轻青蛙们去解决的未解决问题。我向你们挑战，去理解为什么在各种各样的动力学系统中观察到的混沌通常是弱的。

The subject of chaos is characterized by an abundance of quantitative data, an unending supply of beautiful pictures, and a shortage of rigorous theorems. Rigorous theorems are the best way to give a subject intellectual depth and precision. Until you can prove rigorous theorems, you do not fully understand the meaning of your concepts. In the field of chaos I know only one rigorous theorem, proved by Tien-Yien Li and Jim Yorke in 1975 and published in a short paper with the title, “Period Three Implies Chaos”, [4]. The Li-Yorke paper is one of the immortal gems in the literature of mathematics. Their theorem concerns nonlinear maps of an interval onto itself. The successive positions of a point when the mapping is repeated can be considered as the orbit of a classical particle. An orbit has period N if the point returns to its original position after N mappings. An orbit is defined to be chaotic, in this context, if it diverges from all periodic orbits. The theorem says that if a single orbit with period three exists, then chaotic orbits also exist. The proof is simple and short. To my mind, this theorem and its proof throw more light than a thousand beautiful pictures on the basic nature of chaos. The theorem explains why chaos is prevalent in the world. It does not explain why chaos is so often weak. That remains a task for the future. I believe that weak chaos will not be understood in a fundamental way until we can prove rigorous theorems about it.
混沌学科的特点是有大量的定量数据、源源不断的精美图片，但缺乏严格的定理。严格的定理是赋予一个学科 intellectual 深度和精确性的最佳方式。在你能够证明严格的定理之前，你并没有完全理解自己概念的含义。在混沌领域，我只知道一个严格的定理，由李天岩和詹姆斯·约克于1975年证明，并发表在一篇题为《周期三蕴含混沌》的短论文中[4]。李天岩-约克的论文是数学文献中不朽的瑰宝之一。他们的定理涉及区间到自身的非线性映射。当映射重复进行时，一个点的连续位置可以被视为经典粒子的轨道。如果一个点经过 N 次映射后回到原来的位置，那么这个轨道就具有周期 N。在这种情况下，如果一个轨道与所有周期轨道都发散，则定义该轨道是混沌的。该定理指出，如果存在一个周期为三的轨道，那么也存在混沌轨道。证明既简单又简短。在我看来，这个定理及其证明比一千张精美图片更能揭示混沌的基本性质。这个定理解释了为什么混沌在世界上普遍存在，但它没有解释为什么混沌往往是弱的。这仍然是未来的一项任务。我相信，除非我们能证明关于弱混沌的严格定理，否则无法从根本上理解弱混沌。

String Theorists

弦理论家

I would like to say a few words about string theory. Few words, because I know very little about string theory. I never took the trouble to learn the subject or to work on it myself. But when I am at home at the Institute for Advanced Study in Princeton, I am surrounded by string theorists, and I sometimes listen to their conversations. Occasionally I understand a little of what they are saying. Three things are clear. First, what they are doing is first-rate mathematics. The leading pure mathematicians, people like Michael Atiyah and Isadore Singer, love it. It has opened up a whole new branch of mathematics, with new ideas and new problems. Most remarkably, it gave the mathematicians new methods to solve old problems that were previously unsolvable. Second, the string theorists think of themselves as physicists rather than mathematicians. They believe that their theory describes something real in the physical world. And third, there is not yet any proof that the theory is relevant to physics. The theory is not yet testable by experiment. The theory remains in a world of its own, detached from the rest of physics. String theorists make strenuous efforts to deduce consequences of the theory that might be testable in the real world, so far without success.
我想简单谈谈弦理论。说几句就好，因为我对弦理论知之甚少。我从未费心去学习这门学科，也没有亲自研究过它。但当我在普林斯顿高等研究院的家中时，身边都是弦理论家，我有时会听他们交谈，偶尔能听懂一点他们在说什么。有三件事是清楚的。第一，他们所做的是一流的数学。顶尖的纯数学家，如迈克尔·阿蒂亚和艾萨多尔·辛格，都热爱它。它开辟了一个全新的数学分支，带来了新的思想和新的问题。最值得注意的是，它为数学家提供了解决以前无法解决的老问题的新方法。第二，弦理论家认为自己是物理学家，而不是数学家。他们相信自己的理论描述了物理世界中某种真实的东西。第三，还没有任何证据表明该理论与物理学相关。这个理论还不能通过实验来检验，它仍然处于一个独立的世界，与物理学的其他部分脱节。弦理论家们努力推导出该理论可能在现实世界中可检验的结果，但到目前为止还没有成功。

My colleagues Ed Witten and Juan Maldacena and others who created string theory are birds, flying high and seeing grand visions of distant ranges of mountains. The thousands of humbler practitioners of string theory in universities around the world are frogs, exploring fine details of the mathematical structures that birds first saw on the horizon. My anxieties about string theory are sociological rather than scientific. It is a glorious thing to be one of the first thousand string theorists, discovering new connections and pioneering new methods. It is not so glorious to be one of the second thousand or one of the tenth thousand. There are now about ten thousand string theorists scattered around the world. This is a dangerous situation for the tenth thousand and perhaps also for the second thousand. It may happen unpredictably that the fashion changes and string theory becomes unfashionable. Then it could happen that nine thousand string theorists lose their jobs. They have been trained in a narrow specialty, and they may be unemployable in other fields of science.
我的同事爱德华·威滕、胡安·马尔达西那以及其他创立弦理论的人都是鸟，他们翱翔高空，能看到远方山脉的宏伟景象。世界各地大学里成千上万谦逊的弦理论从业者是青蛙，他们探索着鸟们首先在视野中发现的数学结构的细微之处。我对弦理论的担忧是社会学层面的，而非科学层面的。成为最初的一千名弦理论家之一，发现新的联系并开创新的方法，是一件光荣的事情。但成为第二批一千名或第十批一千名弦理论家之一，就不那么光荣了。现在全世界大约有一万名弦理论家。对于第十批一千名，或许还有第二批一千名弦理论家来说，这是一种危险的情况。潮流可能会出人意料地发生变化，弦理论可能会变得不再流行。到那时，可能会有九千名弦理论家失业。他们接受的是狭隘专业的训练，可能无法在其他科学领域找到工作。

Why are so many young people attracted to string theory? The attraction is partly intellectual. String theory is daring and mathematically elegant. But the attraction is also sociological. String theory is attractive because it offers jobs. And why are so many jobs offered in string theory? Because string theory is cheap. If you are the chairperson of a physics department in a remote place without much money, you cannot afford to build a modern laboratory to do experimental physics, but you can afford to hire a couple of string theorists. So you offer a couple of jobs in string theory, and you have a modern physics department. The temptations are strong for the chairperson to offer such jobs and for the young people to accept them. This is a hazardous situation for the young people and also for the future of science. I am not saying that we should discourage young people from working in string theory if they find it exciting. I am saying that we should offer them alternatives, so that they are not pushed into string theory by economic necessity.
为什么这么多年轻人被弦理论吸引？部分原因是智力上的吸引力，弦理论大胆且在数学上优雅。但吸引力也有社会学层面的原因，弦理论之所以有吸引力，是因为它能提供工作。为什么弦理论领域有这么多工作机会？因为弦理论研究成本低。如果你是一个偏远地区物理系的系主任，资金并不充裕，你买不起设备建立现代实验室来做实验物理学研究，但你可以雇得起几个弦理论家。所以你提供几个弦理论方面的工作岗位，就拥有了一个现代物理系。系主任很容易被诱惑提供这样的工作，年轻人也很容易被诱惑接受这样的工作。这对年轻人以及科学的未来来说都是一种危险的情况。我并不是说，如果年轻人觉得弦理论令人兴奋，我们就应该劝阻他们从事弦理论研究。我的意思是，我们应该为他们提供其他选择，这样他们就不会因为经济上的必要性而被迫进入弦理论领域。

Finally, I give you my own guess for the future of string theory. My guess is probably wrong. I have no illusion that I can predict the future. I tell you my guess, just to give you something to think about. I consider it unlikely that string theory will turn out to be either totally successful or totally useless. By totally successful I mean that it is a complete theory of physics, explaining all the details of particles and their interactions. By totally useless I mean that it remains a beautiful piece of pure mathematics. My guess is that string theory will end somewhere between complete success and failure. I guess that it will be like the theory of Lie groups, which Sophus Lie created in the nineteenth century as a mathematical framework for classical physics. So long as physics remained classical, Lie groups remained a failure. They were a solution looking for a problem. But then, fifty years later, the quantum revolution transformed physics, and Lie algebras found their proper place. They became the key to understanding the central role of symmetries in the quantum world. I expect that fifty or a hundred years from now another revolution in physics will happen, introducing new concepts of which we now have no inkling, and the new concepts will give string theory a new meaning. After that, string theory will suddenly find its proper place in the universe, making testable statements about the real world. I warn you that this guess about the future is probably wrong. It has the virtue of being falsifiable, which according to Karl Popper is the hallmark of a scientific statement. It may be demolished tomorrow by some discovery coming out of the Large Hadron Collider in Geneva.
最后，我来谈谈自己对弦理论未来的猜测。我的猜测很可能是错误的，我并没有预测未来的幻想。我告诉你们我的猜测，只是为了给你们一些思考的东西。我认为弦理论既不太可能完全成功，也不太可能完全无用。我说的完全成功，是指它成为一个完整的物理学理论，解释粒子及其相互作用的所有细节。我说的完全无用，是指它仍然只是一门美丽的纯数学。我的猜测是，弦理论的结局将介于完全成功和失败之间。我猜它会像李群理论一样，索菲斯·李在19世纪创建李群理论作为经典物理学的数学框架。只要物理学还是经典的，李群就一直没有成功，它们是一个有待解决的问题的解决方案。但50年后，量子革命改变了物理学，李代数找到了自己合适的位置，它们成为理解对称性在量子世界中核心作用的关键。我预计，50年或100年后，物理学将发生另一场革命，引入我们现在毫无头绪的新概念，这些新概念将赋予弦理论新的意义。在那之后，弦理论将突然在宇宙中找到合适的位置，对现实世界做出可检验的陈述。我要提醒你们，这个关于未来的猜测很可能是错误的。它的优点是可证伪性，根据卡尔·波普尔的观点，这是科学陈述的标志。它可能会被日内瓦大型强子对撞机的某些新发现推翻。

Manin Again

再谈马宁

To end this talk, I come back to Yuri Manin and his book Mathematics as Metaphor. The book is mainly about mathematics. It may come as a surprise to Western readers that he writes with equal eloquence about other subjects such as the collective unconscious, the origin of human language, the psychology of autism, and the role of the trickster in the mythology of many cultures. To his compatriots in Russia, such many-sided interests and expertise would come as no surprise. Russian intellectuals maintain the proud tradition of the old Russian intelligentsia, with scientists and poets and artists and musicians belonging to a single community. They are still today, as we see them in the plays of Chekhov, a group of idealists bound together by their alienation from a superstitious society and a capricious government. In Russia, mathematicians and composers and film- producers talk to one another, walk together in the snow on winter nights, sit together over a bottle of wine, and share each others’ thoughts.
为了结束这次演讲，我再回到尤里·马宁和他的《作为隐喻的数学》一书。这本书主要是关于数学的。西方读者可能会惊讶地发现，他同样雄辩地论述了其他主题，如集体无意识、人类语言的起源、自闭症心理学以及“骗子”在许多文化神话中的角色。对他的俄罗斯同胞来说，这样广泛的兴趣和专长并不令人惊讶。俄罗斯知识分子保持着旧俄罗斯知识阶层的光荣传统，科学家、诗人、艺术家和音乐家属于一个单一的群体。直到今天，就像我们在契诃夫的戏剧中看到的那样，他们是一群理想主义者，因与迷信的社会和反复无常的政府格格不入而团结在一起。在俄罗斯，数学家、作曲家和电影制片人相互交流，在冬夜的雪地里一起散步，一起坐在桌前喝着酒，分享彼此的想法。

Manin is a bird whose vision extends far beyond the territory of mathematics into the wider landscape of human culture. One of his hobbies is the theory of archetypes invented by the Swiss psychologist Carl Jung. An archetype, according to Jung, is a mental image rooted in a collective unconscious that we all share. The intense emotions that archetypes carry with them are relics of lost memories of collective joy and suffering. Manin is saying that we do not need to accept Jung’s theory as true in order to find it illuminating.
马宁是一只鸟，他的视野远远超出了数学领域，延伸到更广阔的人类文化领域。他的爱好之一是瑞士心理学家卡尔·荣格发明的原型理论。根据荣格的观点，原型是植根于我们所有人共有的集体无意识中的心理意象。原型所承载的强烈情感是集体欢乐和痛苦的失落记忆的遗迹。马宁说，我们不必接受荣格的理论为真理，也能发现它富有启发性。

More than thirty years ago, the singer Monique Morelli made a recording of songs with words by Pierre MacOrlan. One of the songs is La Ville Morte, the dead city, with a haunting melody tuned to Morelli’s deep contralto, with an accordion singing counterpoint to the voice, and with verbal images of extraordinary intensity. Printed on the page, the words are nothing special:
三十多年前，歌手莫妮克·莫雷利录制了一张由皮埃尔·马克奥兰作词的歌曲专辑。其中一首歌是《死亡之城》，旋律萦绕不去，与莫雷利低沉的女低音相协调，手风琴与歌声形成对位，歌词意象也极具冲击力。但印在纸上，这些歌词并没有什么特别之处：

“En pénétrant dans la ville morte,
Je tenait Margot par le main…
Nous marchions de la nécropole,
Les pieds brisés et sans parole,
Devant ces portes sans cadole,
Devant ces trous indéfinis,
Devant ces portes sans parole
Et ces poubelles pleines de cris”.
“当我们走进死亡之城，
我牵着玛戈的手……
我们从墓地走来，
脚步沉重，一言不发，
在这些没有锁的门面前，
在这些模糊不清的洞穴面前，
在这些沉默的门面前，
在这些装满尖叫的垃圾桶面前。”

“As we entered the dead city, I held Margot by the hand…We walked from the graveyard on our bruised feet, without a word, passing by these doors without locks, these vaguely glimpsed holes, these doors without a word, these garbage cans full of screams.”
“当我们走进死亡之城，我牵着玛戈的手……我们拖着受伤的脚从墓地走来，一言不发，走过这些没有锁的门、这些隐约可见的洞穴、这些沉默的门、这些装满尖叫的垃圾桶。”

I can never listen to that song without a disproportionate intensity of feeling. I often ask myself why the simple words of the song seem to resonate with some deep level of unconscious memory, as if the souls of the departed are speaking through Morelli’s music. And now unexpectedly in Manin’s book I find an answer to my question. In his chapter, “The Empty City Archetype”, Manin describes how the archetype of the dead city appears again and again in the creations of architecture, literature, art and film, from ancient to modern times, ever since human beings began to congregate in cities, ever since other human beings began to congregate in armies to ravage and destroy them. The character who speaks to us in MacOrlan’s song is an old soldier who has long ago been part of an army of occupation. After he has walked with his wife through the dust and ashes of the dead city, he hears once more:
我每次听到那首歌，心中都会涌起一种难以抑制的强烈情感。我常常自问，为何那首歌的朴实歌词似乎能与某种深层的潜意识记忆产生共鸣，仿佛逝者的灵魂正借着莫雷利的音乐诉说着什么。而现在，我在曼宁的书中意外找到了这个问题的答案。在他《空城原型》这一章中，曼宁阐述了“死城”这一原型如何在从古代到现代的建筑、文学、艺术和电影作品中反复出现——自人类开始聚集于城市，自其他人类开始聚集为军队去蹂躏和摧毁这些城市以来，这种原型就从未消失。马克奥兰歌曲中与我们对话的角色是一位老兵，他曾是占领军的一员。在他和妻子走过死亡之城的尘土与灰烬后，他再次听到：

“Chansons de charme d’un clairon
Qui fleurissait une heure lointaine
Dans un rêve de garnison”.
“号角的迷人歌声
在遥远的时刻绽放
在驻军的梦境中”

“The magic calls of a bugle that came to life for an hour in an old soldier’s dream”.
“号角的神奇召唤，在一位老兵的梦中苏醒了一小时”

The words of MacOrlan and the voice of Morelli seem to be bringing to life a dream from our collective unconscious, a dream of an old soldier wandering through a dead city. The concept of the collective unconscious may be as mythical as the concept of the dead city. Manin’s chapter describes the subtle light that these two possibly mythical concepts throw upon each other. He describes the collective unconscious as an irrational force that powerfully pulls us toward death and destruction. The archetype of the dead city is a distillation of the agonies of hundreds of real cities that have been destroyed since cities and marauding armies were invented. Our only way of escape from the insanity of the collective unconscious is a collective consciousness of sanity, based upon hope and reason. The great task that faces our contemporary civilization is to create such a collective consciousness.
马克奥兰的歌词和莫雷利的歌声似乎将我们集体无意识中的一个梦境唤醒，一个老兵在死亡之城徘徊的梦境。集体无意识的概念可能与死亡之城的概念一样具有神话色彩。马宁的章节描述了这两个可能具有神话色彩的概念相互投射出的微妙光芒。他将集体无意识描述为一种非理性的力量，强烈地将我们推向死亡和毁灭。死亡之城的原型是自城市和掠夺性军队出现以来，数百座被摧毁的真实城市所经历痛苦的浓缩。我们摆脱集体无意识疯狂的唯一途径，是建立在希望和理性基础上的集体理性意识。我们当代文明面临的伟大任务，就是创造这样一种集体意识。

References

参考文献

[1] M.J. BERTIN ET AL., Pisot and Salem Numbers, Birkhauser Verlag, Basel, 1992.
[1] M.J. 贝尔廷等，《皮索特与塞勒姆数》，伯克霍夫出版社，巴塞尔，1992年。

[2] M.L. CARTWRIGHT and J.E. LITTLEWOOD, On nonlinear differential equations of the second order, I, Jour. London Math. Soc. 20 (1945), 180-189.
[2] M.L. 卡特赖特与J.E. 利特尔伍德，《关于二阶非线性微分方程》（第一部分），《伦敦数学会杂志》第20卷（1945年），第180-189页。

[3] FREEMAN DYSON, Prof. Hermann Weyl, For. Mem. R. S. Nature 177 (1956), 457-458.
[3] 弗里曼·戴森，《赫尔曼·外尔教授》，《自然》杂志第177卷（1956年），第457-458页。

[4] TIEN-YIEN LI and JAMES A. YORKE, Period three implies chaos, Amer. Math. Monthly 82 (1975), 985-992.
[4] 李天岩与詹姆斯·A. 约克，《周期三蕴含混沌》，《美国数学月刊》第82卷（1975年），第985-992页。

[5] YURI I. MANIN, Mathematics as Metaphor: Selected Essays, American Mathematical Society, Providence, Rhode Island, 2007. [The Russian version is: MANIN, Yu. I, Matematika kak Metafora, Moskva, Izdatyelstvo MTsNMO, 2008.]
[5] 尤里·I. 马宁，《作为隐喻的数学：文选》，美国数学会，普罗维登斯，罗得岛州，2007年。[俄文版：马宁，《数学作为隐喻》，莫斯科，MTsNMO出版社，2008年。]

[6] ANDREW M. ODLYZKO, Primes, quantum chaos and computers, in Number Theory, Proceedings of a Symposium, National Research Council, Washington DC, 1990, pp. 35-46.
[6] 安德鲁·M. 奥德里兹科，《素数、量子混沌与计算机》，收录于《数论：研讨会论文集》，国家研究委员会，华盛顿特区，1990年，第35-46页。

[7] HERMANN WEYL, Gravitation und elektrizitat, Sit. Konig. Preuss. Akad. Wiss. 26 (1918), 465-480.
[7] 赫尔曼·外尔，《引力与电》，《普鲁士皇家科学院会议报告》第26卷（1918年），第465-480页。

[8] --, Elektron und gravitation, Zeits. Phys. 56 (1929), 350-352.
[8] --，《电子与引力》，《物理杂志》第56卷（1929年），第350-352页。

[9] --, Selecta, Birkhauser Verlag, Basel, 1956, p. 192.
[9] --，《选集》，伯克霍夫出版社，巴塞尔，1956年，第192页。

[10] CHEN NING YANG, Integral formalism for gauge fields, Phys. Rev. Letters 33 (1974), 445-447.
[10] 杨振宁，《规范场的积分形式》，《物理评论快报》第33卷（1974年），第445-447页。

[11] CHEN NING YANG and ROBERT L. MILLS, conservation of isotopic spin and isotopic gauge invariance, Phys. Rev. 96 (1954), 191-195.
[11] 杨振宁与罗伯特·L. 米尔斯，《同位旋守恒与同位规范不变性》，《物理评论》第96卷（1954年），第191-195页。

[12] --, Hermann Weyl’s contribution to physics, in Hermann Weyl, 1885-1985, (K. Chandrasekharan, ed.), Springer-Verlag, Berlin, 1986, p. 19.
[12] --，《赫尔曼·外尔对物理学的贡献》，收录于《赫尔曼·外尔，1885-1985》（K. 钱德拉塞卡兰编），施普林格出版社，柏林，1986年，第19页。

---

Dyson on Birds and Frogs

戴森谈鸟类和青蛙

Posted on January 7, 2009 by woit

Next month’s Notices of the AMS has an essay by Freeman Dyson entitled Frogs and Birds, which was written for his planned Einstein Public Lecture. In it, he divides mathematicians up into two species: birds, who “fly high in the air and survey broad vistas” (i.e., seek abstraction, unification, and generalization), and frogs, who “see only the flowers that grow nearby” (i.e., study the details of specific examples).
下个月的《美国数学会通报》（Notices of the AMS）将刊登弗里曼·戴森（Freeman Dyson）的文章《青蛙与鸟类》。这篇文章是为他计划中的爱因斯坦公开讲座而写的。在文章中，他将数学家分为两类：一类是“鸟类”，它们“在高空中飞翔，俯瞰广阔的视野”（即追求抽象、统一和概括）；另一类是“青蛙”，它们“只能看到附近生长的花朵”（即专注于研究具体例子的细节）。

Dyson himself is resolutely a frog, but writes that “many of my best friends are birds,” and argues that both birds and frogs are needed to do justice to the breadth and depth of the subject of mathematics. Frog that he is, his essay covers a variety of quite different special topics that have drawn his attention, linked together only weakly by the bird/frog theme. These include a discussion of the roles of complex numbers and linearity in quantum mechanics, a proposed idea about how to attack the Riemann hypothesis (try and enumerate 1D-quasicrystals, since the zeros of the zeta function have this structure), and a collection of profiles and anecdotes about various mathematicians and physicists (Besicovitch, Weyl, Yang, Manin, von Neumann).
戴森本人坚定地属于“青蛙”阵营，但他也写道“我最好的许多朋友都是鸟类”，并认为需要鸟类和青蛙来公正地对待数学学科的广度和深度。尽管他是青蛙，但他的文章涵盖了各种完全不同的特殊主题，这些主题仅通过“鸟类/青蛙”的主题微弱地联系在一起。其中包括对复数和线性在量子力学中的作用的讨论，关于如何攻克黎曼猜想的提议（尝试枚举一维准晶体，因为黎曼ζ函数的零点具有这种结构），以及关于各种数学家和物理学家（贝西科维奇、外尔、杨振宁、马宁、冯·诺依曼）的简介和轶事。

Personally I suppose I fit well into Dyson’s bird category, but among the best mathematicians that I know, the frog/bird distinction is often unclear. Many of them make their reputation by proving rather abstract and general theorems, but these proofs are often the result of a huge amount of detailed investigation of examples. I agree with Dyson that both points of view are needed, and see the most successful cases of progress in mathematics coming from mathematicians who avoid the temptation to fly too high into arid abstraction or sink too deep into irrelevant detail.
就我个人而言，我认为自己很适合戴森所说的“鸟类”范畴。然而，在我所认识的顶尖数学家中，青蛙与鸟类的区别往往并不明显。他们中的许多人通过证明相当抽象和一般的定理而声名鹊起，但这些证明通常是基于对大量具体例子的详细研究。我同意戴森的观点，即这两种视角都是必需的，并且认为数学中最成功的进展往往来自于那些避免陷入枯燥的抽象或无关紧要的细节的数学家。

Dyson includes a long section on string theory, which I’ll include here:
戴森在文章中还专门用了一段较长的篇幅来讨论弦理论，我将其内容摘录如下：

I would like to say a few words about string theory. Few words, because I know very little about string theory. I never took the trouble to learn the subject or to work on it myself. But when I am at home at the Institute for Advanced Study in Princeton, I am surrounded by string theorists, and I sometimes listen to their conversations. Occasionally I understand a little of what they are saying. Three things are clear. First, what they are doing is first-rate mathematics. The leading pure mathematicians, people like Michael Atiyah and Isadore Singer, love it. It has opened up a whole new branch of mathematics, with new ideas and new problems. Most remarkably, it gave the mathematicians new methods to solve old problems that were previously unsolvable. Second, the string theorists think of themselves as physicists rather than mathematicians. They believe that their theory describes something real in the physical world. And third, there is not yet any proof that the theory is relevant to physics. The theory is not yet testable by experiment. The theory remains in a world of its own, detached from the rest of physics. String theorists make strenuous efforts to deduce consequences of the theory that might be testable in the real world, so far without success.
我想说几句关于弦理论的话。几句话而已，因为我对弦理论知之甚少。我从未费心去学习这个领域，也没有亲自去研究它。但当我身处普林斯顿高等研究院时，我周围都是弦理论家，我有时会听他们的谈话。偶尔我能听懂他们在说什么。有三件事是明确的。首先，他们正在做的是一流的数学。领先的纯数学家，如迈克尔·阿蒂亚（Michael Atiyah）和伊萨多尔·辛格（Isadore Singer）等人都非常喜欢它。它开辟了一个全新的数学分支，带来了新的思想和新的问题。最引人注目的是，它为数学家提供了解决以前无法解决的旧问题的新方法。其次，弦理论家认为自己是物理学家而不是数学家。他们相信自己的理论描述了物理世界中真实存在的某种东西。第三，目前还没有任何证据表明该理论与物理学相关。该理论还无法通过实验来验证。它仍然处于一个与物理学其他部分相分离的独立世界中。弦理论家们正在努力推导出该理论在现实世界中可验证的后果，但到目前为止还没有成功。

My colleagues Ed Witten and Juan Maldacena and others who created string theory are birds, flying high and seeing grand visions of distant ranges of mountains. The thousands of humbler practitioners of string theory in universities around the world are frogs, exploring fine details of the mathematical structures that birds first saw on the horizon. My anxieties about string theory are sociological rather than scientific. It is a glorious thing to be one of the first thousand string theorists, discovering new connections and pioneering new methods. It is not so glorious to be one of the second thousand or one of the tenth thousand. There are now about ten thousand string theorists scattered around the world. This is a dangerous situation for the tenth thousand and perhaps also for the second thousand. It may happen unpredictably that the fashion changes and string theory becomes unfashionable. Then it could happen that nine thousand string theorists lose their jobs. They have been trained in a narrow specialty, and they may be unemployable in other fields of science.
我的同事埃德·维滕（Ed Witten）和胡安·马尔达塞纳（Juan Maldacena）以及其他创立弦理论的人是“鸟类”，他们飞得很高，看到了远处山脉的宏伟远景。世界各地大学里成千上万的弦理论实践者则是“青蛙”，他们正在探索“鸟类”在地平线上首次看到的数学结构的细节。我对弦理论的担忧是社会学方面的，而不是科学方面的。成为第一千名弦理论家之一，发现新的联系并开拓新的方法，这是一件非常荣耀的事情。但成为第二千名或第一万名弦理论家则没有那么荣耀了。目前，全球大约有一万名弦理论家。对于第一万名弦理论家来说，这可能是一个危险的局面，对于第二千名来说也许也是如此。弦理论可能会突然失宠，这并非不可能。如果弦理论不再流行，那么可能会有九千名弦理论家失业。他们接受的是狭窄的专业训练，在其他科学领域可能找不到工作。

Why are so many young people attracted to string theory? The attraction is partly intellectual. String theory is daring and mathematically elegant. But the attraction is also sociological. String theory is attractive because it offers jobs. And why are so many jobs offered in string theory? Because string theory is cheap. If you are the chairperson of a physics department in a remote place without much money, you cannot afford to build a modern laboratory to do experimental physics, but you can afford to hire a couple of string theorists. So you offer a couple of jobs in string theory, and you have a modern physics department. The temptations are strong for the chairperson to offer such jobs and for the young people to accept them. This is a hazardous situation for the young people and also for the future of science. I am not saying that we should discourage young people from working in string theory if they find it exciting. I am saying that we should offer them alternatives, so that they are not pushed into string theory by economic necessity.
为什么这么多年轻人会被弦理论吸引呢？部分原因是出于对知识的热爱。弦理论是大胆的，并且在数学上非常优雅。但这种吸引力也与社会因素有关。弦理论之所以有吸引力，是因为它提供了工作岗位。为什么弦理论能提供这么多工作岗位呢？因为弦理论不需要太多资金投入。如果你是一个偏远地区的物理系主任，手头资金有限，你无法负担建造一个现代化实验室来进行实验物理研究，但你可以雇用几位弦理论家。只要你提供几个弦理论的岗位，你的物理系看起来就“现代化”了。系主任提供这些岗位的诱惑很大，年轻人接受这些岗位的诱惑也很大。这对年轻人来说是一个危险的局面，对科学的未来也是如此。我不是说，如果年轻人觉得弦理论令人兴奋，我们就应该阻止他们从事弦理论的研究。我是说，我们应该为他们提供其他选择，这样他们就不会仅仅因为经济原因而被迫进入弦理论领域。

Finally, I give you my own guess for the future of string theory. My guess is probably wrong. I have no illusion that I can predict the future. I tell you my guess, just to give you something to think about. I consider it unlikely that string theory will turn out to be either totally successful or totally useless. By totally successful I mean that it is a complete theory of physics, explaining all the details of particles and their interactions. By totally useless I mean that it remains a beautiful piece of pure mathematics. My guess is that string theory will end somewhere between complete success and failure. I guess that it will be like the theory of Lie groups, which Sophus Lie created in the nineteenth century as a mathematical framework for classical physics. So long as physics remained classical, Lie groups remained a failure. They were a solution looking for a problem. But then, fifty years later, the quantum revolution transformed physics, and Lie algebras found their proper place. They became the key to understanding the central role of symmetries in the quantum world. I expect that fifty or a hundred years from now another revolution in physics will happen, introducing new concepts of which we now have no inkling, and the new concepts will give string theory a new meaning. After that, string theory will suddenly find its proper place in the universe, making testable statements about the real world. I warn you that this guess about the future is probably wrong. It has the virtue of being falsifiable, which according to Karl Popper is the hallmark of a scientific statement. It may be demolished tomorrow by some discovery coming out of the Large Hadron Collider in Geneva.
最后，我给大家讲讲我对弦理论未来的猜测。我的猜测很可能是错误的。我并不认为自己能够预测未来。我之所以告诉你们我的猜测，只是想给你们提供一个思考的方向。我认为弦理论既不会完全成功，也不会完全失败。我所说的“完全成功”是指它成为一个完整的物理学理论，能够解释粒子及其相互作用的所有细节；而“完全失败”是指它仅仅是一篇美丽的纯数学论文。我的猜测是，弦理论最终会处于成功与失败之间。我猜它会像李群理论一样。19 世纪，索菲斯·李（Sophus Lie）创立了李群理论，将其作为经典物理学的数学框架。只要物理学仍然是经典的，李群理论就是一个失败。它是一个在寻找问题的解决方案。然而，五十年后，量子革命改变了物理学，李代数找到了它应有的位置。它成为理解量子世界中对称性核心作用的关键。我预计，五十年或一百年后，物理学将发生另一场革命，引入我们现在无法想象的新概念，而这些新概念将赋予弦理论新的意义。之后，弦理论将突然在宇宙中找到它应有的位置，对现实世界做出可检验的陈述。我警告大家，我对未来的这个猜测很可能是错误的。不过，它有一个优点，那就是可以被证伪。根据卡尔·波普尔（Karl Popper）的观点，这是科学命题的标志。也许明天，日内瓦的大型强子对撞机（Large Hadron Collider）就会有一个发现推翻我的猜测。

I don’t know where Dyson got the estimate of ten thousand string theorists; my own estimate would be more like one to two thousand (with the number strongly dependent on how you decide who is a “string theorist”). The large yearly Strings200X conferences that bring together a sizable fraction of the active string theory community tend to draw roughly 500 people.
我不知道戴森是从哪里得到全球有一万名弦理论家的估计数字的；我自己估计大概有一千到两千名（这个数字很大程度上取决于你如何定义“弦理论家”）。每年举办的大型弦理论会议（Strings200X）会吸引相当一部分活跃的弦理论家，参会人数通常在五百人左右。

The Princeton-centric assumption that there are lots of string theory jobs embedded in his question “And why are so many jobs offered in string theory?” is quite problematic, as any young string theorist on the job market could explain to him. There actually aren’t a lot of string theory jobs out there, and a lot of Ph.D.s in the subject being produced, leading to a lot of ex-string theorists now working in the financial industry and elsewhere. These days, if you are going to choose your field based on where the jobs are, you become an LHC phenomenologist or a cosmologist. If you want to be a string theorist, you better be a string phenomenologist or a string cosmologist. Also rather unrealistic is Dyson’s “it could happen that nine thousand string theorists lose their jobs,” due to tenure in the academic system. Even if a consensus develops over the next few years that string theory was all a big mistake, twenty years from now there will still be a cadre of (older) people working in the field.
戴森在文章中提出的问题“为什么弦理论提供了这么多工作岗位？”似乎是以普林斯顿为中心的假设，这在任何一位正在求职的年轻弦理论家看来都是有问题的。事实上，弦理论的工作岗位并不多，但该领域的博士学位获得者却不少，这导致许多前弦理论家如今在金融行业或其他领域工作。如今，如果你要根据工作机会来选择研究领域，你可能会成为一名大型强子对撞机（LHC）现象学家或宇宙学家。如果你想成为一名弦理论家，你最好专注于弦现象学或弦宇宙学。同样不切实际的是戴森所说的“可能会有九千名弦理论家失业”，因为在学术体系中，终身教职的存在使得这种情况不太可能发生。即使在未来几年内形成共识，认为弦理论是一个巨大的错误，二十年后仍然会有一批（年长的）人在该领域工作。

Dyson’s idea, that 50 - 100 years from now, a new revolution in physics will show how string theory fits in may be right. It also may be that this has already happened, as much of the field has moved into the study of gauge-string dualities, where string theory provides a useful approximation for strongly coupled systems, and the idea that it unifies particle physics is falling by the wayside.
戴森认为，50 - 100 年后，物理学的新革命将展示弦理论如何适应，这种观点可能是正确的。但也有可能这种情况已经发生了，因为该领域的许多研究已经转向规范 - 弦对偶性，弦理论为强耦合系统提供了有用的近似，而它统一粒子物理学的观点正在被逐渐抛弃。

Responses to Dyson on Birds and Frogs

《戴森谈鸟类和青蛙》的回复

1. Rene Meyer says:
   January 8, 2009 at 2:39 am

   Dear Peter,

   Thanks for pointing out that nice piece of an essay. As a stringy person myself I would however disagree with Dyson saying that string theorists are too narrowly trained to be useful in other parts of science. People who enter a PhD program in string theory in a reknown place (need not to be Princeton) are good physicists already from their undergrad time, as the students normally interested in string theory are interested in deep questions of physics in general, and for this they need to understand the basics of physics to a good extend, which in turn means they have done their homework already as an undergrad. This is at least my experience. So they are well-trained physicists, and can in principle with some preparation time work in any field of theoretical physics. Also, for understanding the implications of string theory one needs to be well-trained in nearly all subjects of basic theoretical physics, which there are mathematical methods, classical and quantum field theory, statistical physics and gravity/GR. The average string theorist is well-trained in all these subjects. What makes the change of subject away from string theory even to closely related areas like “quantum gravity” (for the purpose here just summarizing all attempts to quantum gravity except string theory), classical gravity or pure cosmology is, in my experience, rather the attitude of other communities towards string theory, which is often full of prejudices originating from hearsay, the failure to understand even the stringy basics and the dissatisfaction thus created. It’s often a one-way road: String theorists understand what other people are doing, but the other people don’t understand string theory. With such a structure, it is nearly impossible to change for a postdoc in a different field, as everybody takes only the people whose work he knows and understands. This is partly also true in string theory, of course.
   感谢您分享这篇精彩的文章。然而，作为一名弦理论研究者，我不同意戴森说弦理论家的训练过于狭窄，无法在科学的其他领域发挥作用。在知名学府（不一定是普林斯顿）攻读弦理论博士学位的学生，从本科时期就已经是优秀的物理学家了。因为通常对弦理论感兴趣的学生对物理学的深层问题感兴趣，而要理解这些问题，他们需要很好地掌握物理学的基础知识，这反过来又意味着他们在本科时就已经做好了准备。至少在我的经验中是这样的。因此，他们是训练有素的物理学家，原则上只要有一定的准备时间，就可以在理论物理学的任何领域工作。此外，要理解弦理论的含义，人们需要在几乎所有基础理论物理学的学科中接受良好的训练，包括数学方法、经典场论和量子场论、统计物理学以及引力 / 广义相对论。普通的弦理论家在所有这些学科上都受过良好的训练。根据我的经验，使他们难以从弦理论转向密切相关的领域（例如“量子引力”——这里只是总结除弦理论之外的所有量子引力尝试）、经典引力或纯粹宇宙学的原因，往往是其他领域对弦理论的态度。这种态度往往充满了源自道听途说的偏见，甚至无法理解弦理论的基础知识，从而产生不满。这通常是一条单行道：弦理论家了解其他人在做什么，但其他人不了解弦理论。在这种情况下，对于不同领域的博士后来说，几乎不可能改变，因为每个人都只选择他熟悉并理解其工作的人。当然，在弦理论中也部分如此。

   Another remark: Not only string theory is cheap, whole theoretical physics is, if you don’t need supercomputers. So poorer universities can hire also other people…
   另一个观点：如果你不需要超级计算机，不仅弦理论很便宜，整个理论物理学都很便宜。所以，资金不足的大学也可以雇佣其他领域的研究人员……

2. somebody says:
   January 8, 2009 at 7:56 am

   Thanks for Dyson’s interesting article, Peter. The essay was overall balanced I think, so I will state a few issues with which I disagree.
   感谢戴森的有趣文章，彼得。我认为这篇文章总体上是平衡的，所以我将陈述一些我不同意的问题。

3. People don’t go into string theory for jobs. I was very sternly warned that going into string theory is dangerous, careerwise, and no string theorist I know had any illusions about it when they got into it either. I suspect that Dyson is forgetting why he went into mathematics and theoretical physics back when he was an excitable young man, but that’s just my guess.
   人们不是为了工作而进入弦理论。我被非常严厉地警告说，进入弦理论在职业上是危险的，我认识的弦理论家在进入弦理论时也没有对此抱有任何幻想。我怀疑戴森忘记了他为什么在他还是一个兴奋的年轻人时进入数学和理论物理领域，但这只是我的猜测。

4. While agreeing with the possibility that string theory might be only part of the full picture, I would like to point out that since we don’t have the benefit of hindsight, the only working strategy we have available for progress NOW is to push our current theories to their limits. Revolutions, almost by definition, cannot appear on demand. To give an example: It took almost twenty years of work on seemingly pointless things like gauged supergravities, many dimensions, superconformal algebras, large N gauge theories etc. before it all finally came together in gauge-gravity duality.
   虽然我同意弦理论可能只是全貌的一部分，但我想指出，由于我们没有事后诸葛亮的好处，我们现在唯一可用的进步策略就是将我们当前的理论推向极限。几乎根据定义，革命不能按需出现。举个例子：在看似毫无意义的东西上花了近二十年的时间，比如测量超重力、许多维度、超共形代数、大 N 规范理论等，才最终以规范 - 重力对偶性组合在一起。

5. String theory being superspecialized is also a weird claim. One of the challenges that an aspiring string theorist faces is in fact the ridiculous amount of physics and math they have to learn. I think the real problem is not that string theory is superspecialized, but that some string theorists are superspecialized to one subfield or even to one problem. But this is not just a feature of the string theory community …
   弦理论是超级专业化的也是一个奇怪的说法。一个有抱负的弦理论家面临的挑战之一实际上是他们必须学习的物理和数学数量之多。我认为真正的问题不在于弦理论是超级专业化的，而是一些弦理论家对一个子领域甚至一个问题进行了超级专业化。但这不仅仅是弦理论界的一个特征……

6. Peter Woit says:
   January 8, 2009 at 10:01 am

   Rene,

   I agree that Dyson’s explanation that string theorists get hired because they are cheap doesn’t explain anything, since they are no more or less expensive than other theorists.
   我同意戴森关于弦理论家被雇用是因为他们便宜的解释并不能说明任何问题，因为他们并不比其他理论家更便宜或更贵。

   As for the somebody’s point that string theorists don’t go into the subject because job prospects are good, that’s certainly right, more so now than ever. The question though is a relative one. The job situation in theoretical physics in general has been terrible for a long time. If you decide you want to try for a career as a theoretical physicist, despite the odds, does going into string theory maximize your chances? I think now someone who wants to maximize their chances is more likely to go into phenomenology or cosmology. But if your interest is in fundamental, more mathematical and formal approaches, you still may not have any real alternative to string theory. The job situation for string theorists is bad, but jobs in formal theory that is not string theory are pretty much non-existent in physics departments, at least in the US.
   至于有人认为弦理论家不会因为工作前景良好而进入这个主题，这当然是正确的，现在比以往任何时候都更是如此。不过，这个问题是一个相对的问题。长期以来，理论物理学的工作状况总体上一直很糟糕。如果你决定尝试成为一名理论物理学家，尽管困难重重，那么进入弦理论是否能最大限度地提高你的机会？我认为现在想要最大化机会的人更有可能进入现象学或宇宙学。但是，如果你对基础的、更多的数学和形式方法感兴趣，你可能仍然没有任何真正的弦理论替代方案。弦理论家的工作环境很糟糕，但非弦理论的形式理论工作在物理系几乎不存在，至少在美国是这样。

   My impression of the background of string theorists is that it varies widely. Some do actually know a lot of physics and mathematics, and have a good chance of changing fields if they want to. Others don’t, and suffer from the disability of not knowing how little they know, making it highly unlikely that they’ll ever be able to do what it takes to move to another field.
   我对弦理论家背景的印象是千差万别。有些人实际上确实知道很多物理和数学，如果他们愿意的话，很有可能改变领域。其他人则不知道，并且患有不知道自己知道的有多少的残疾，这使得他们不太可能做转移到另一个领域所需的事情。

7. Jonathan Vos Post says:
   January 8, 2009 at 5:21 pm

   I love Dyson’s paper. To me, though, the strong point is the detailed and insightful History of transdisciplinary unifiers in Mathematics, and the surprise that this is useful in understanding Physics. I feel that Context trumps Content here. But I agree with the comments that we’ll have a better idea in 50 - 100 years what this was all about, in the late 20th century. If I’m very lucky, I’ll be here in 50 years (aged 107). Nobody yet has been 157, so I’m not going to invest much effort in what might be known in 100 years.
   我喜欢戴森的论文。不过，对我来说，强项是数学中跨学科统一器的详细而富有洞察力的历史，以及这对理解物理学有用的惊喜。我觉得这里的上下文胜过内容。但我同意这样的评论，即我们将在 50 - 100 年后对 20 世纪末的一切有一个更好的想法。如果我非常幸运的话，我将在 50 年后（107 岁）来到这里。还没有人满 157 岁，所以我不会在 100 年后可能知道的事情上投入太多精力。

---

戴森：鸟与蛙 | 附丘成桐先生缅怀戴森

原创 弗里曼・戴森 数理人文 2020 年 03 月 01 日 21:27

作者简介：弗里曼・戴森（Freeman Dyson）是英国物理学家与数学家，任普林斯顿高等研究院教授凡四十余年，是未取得博士学位却享有隆崇学术地位的特例。戴森兴趣极广，思想广阔，超前时代，是典型的文艺复兴人。科普著作极丰，文章散见于各杂志媒体。

译者简介：赵学信，网站工程师。兼事翻译、写作。

本文系作者为美国数学学会（AMS）2008 年爱因斯坦讲座所准备之讲稿，后因演讲取消而未宣读。原文见Birds and Frogs, Notices of the AMS56(2009), no. 2, 212-223，中译文经作者与 AMS 授权刊载于《数理人文》第 2 期（2014 年 6 月），未经许可，不得转载。

弗里曼・戴森（1923.12.15 – 2020.2.28）| 照片来源：IAS.ORG

丘成桐先生缅怀戴森

戴森可以说是二十世纪最伟大的数学物理学家，他在数学上的重要影响有两个方向，一个方向是通过 Exclusion Principle（不相容原理）来解释物质稳定性的问题，影响了 Elliott Lieb 及 Charles Fefferman 等人一系列的工作。另外一方面他在原子谱上的问题的猜测引发了一连串的 Random Matrix（随机矩阵）理论上的重要发展，由哈佛大学的姚鸿泽解决并且发扬光大。我在普林斯敦高等硏究所做教授时跟他认识，此人见识超凡，但却是平易近人。直到近年九十多岁了，对物理和数学还是有欣赏的能力。我很佩服他。

—— 丘成桐，2020 年 2 月 29 日

有些数学家是飞鸟，其他的是蛙。鸟儿高翔天际，遍览直至天际的广阔数学远景，他们所喜爱的，是能统摄我们的思想、将散布于地上各处的种种问题整合起来的概念。青蛙住在泥地里，只能看到长在附近的花朵。他们喜爱特定事物的细节，一次只解决一个问题。我刚好是一只蛙，但是我的许多好友都是飞鸟。我今晚演讲的主题是这样的：数学需要鸟，也需要蛙。数学既丰富而且优美；因为有飞鸟赋予它宽阔的远景，有蛙儿赋予它精致的细节。数学既是伟大的艺术，也是重要的科学；因为它结合了概念的普遍性和结构的深刻性。倘若有人宣称鸟儿因为看得更辽远而胜过蛙，或是青蛙因为观察更深刻而胜过鸟，两种说法都是愚蠢的。数学的世界既广阔又深刻，我们需要鸟与蛙齐心协力才能探索。

这场演讲称为爱因斯坦讲座（Einstein Lecture）。我很高兴美国数学学会邀我来向爱因斯坦致敬。爱因斯坦不是数学家，而是一位对数学有着爱憎情结的物理学家。他一方面对数学描述大自然运作的能力，有着无比的敬意。他对数学之美有着敏锐的直觉，所以才能循着正确的途径找到自然定律。另一方面，他对纯数学没兴趣，也没有成为数学家的技术能力。他晚年时，以研究助理的名义聘用年轻同事来帮他做数学计算。他的思考方式是物理的，而非数学的。他在物理学家之中，是无比犀利、看得最远的飞鸟。因为我没有什么新意可阐发，关于爱因斯坦我就说到这里。

培根与笛卡儿

十七世纪初有两位伟大的哲学家，英国的培根（Francis Bacon）和法国的笛卡儿（René Descartes），宣告了现代科学的诞生。笛卡儿是鸟，而培根则是蛙。两人分别描述各自所看到的未来，而他们所看到的非常不同。培根说：“一切取决于目光紧盯住大自然的事实。” 笛卡儿则说：“我思，故我在。” 根据培根的观点，科学家应该游历各地，搜集事实，直到所积累的事实足以彰显大自然如何运作，然后科学家再从事实中归纳出大自然所遵循的定律。根据笛卡儿的观点，科学家应该待在家里，纯由思考推导出自然律。要正确地推导定律，科学家只需要逻辑法则，并且确知上帝存在即可。自培根、笛卡儿以来四百年，科学同时循着这两条道路奋进。单凭培根的经验主义或笛卡儿的教条主义（dogmatism），都无法阐明大自然的奥祕，然而一旦两者合并，则有惊人的成效。四百年来，英国科学家倾向于培根，法国科学家则倾向于笛卡儿。法拉第、达尔文和卢瑟福（Ernest Rutherford）是培根主义者，帕斯卡（Blaise Pascal）、拉普拉斯（Pierre-Simon Laplace）和庞加莱（Henri Poincaré）是笛卡儿主义者。这两种对比明显的文化彼此相互浇灌，大大丰盈了科学本身。两种文化也始终并存于两国。牛顿本质上是笛卡儿主义者，他按笛卡儿的想法使用纯粹思考，却摧毁了笛卡儿的涡流说教条。居里夫人（Marie Curie）本质上是培根主义者，她烧融了数以吨计的原铀矿，结果摧毁了原子不灭的教条。

二十世纪数学史上有两桩决定性的事件，其中之一属于培根主义传统，另一桩属于笛卡儿主义传统。第一个事件是 1900 年在巴黎举办的世界数学家大会（ICM），希尔伯特（David Hilbert）在该次大会的全会演讲中，提出了他著名的 23 个未解问题，指引出数学在新世纪的发展途径。希尔伯特本人像是鸟儿，高高飞翔在整个数学领域的上空，但他提出问题的对象是青蛙型的数学家，让他们一次解决一个问题。第二个决定性事件是 1930 年代在法国由一群飞鸟型数学家组成的布巴基社群（Bourbaki group）。他们致力于出版一系列的教科书，以期建立起统合所有数学的架构。希尔伯特问题非常成功地指引数学研究走向丰硕的发展方向。其中有些问题已解决，有些仍然未解，但几乎每一个问题都激发出数学的新理念和新领域。布巴基计划同样也是影响深远。它改变了其后五十年的数学风格，赋予数学先前不曾存在的逻辑一贯性，把强调的重点从具体实例转移到抽象一般性。在布巴基擘画的架构下，数学就是写在布巴基教科书里的抽象结构，不在书里的就不是数学。具体实例既然没出现在书里，所以不是数学。布巴基纲领是笛卡儿风格的极致表现。它摒弃了培根主义旅人沿途采集的花朵，从而窄化了数学的视域。

大自然的玩笑

以我这样的培根主义者来看，布巴基纲领遗漏的东西最主要的是惊奇的要素。布巴基纲领试图让数学的一切合乎逻辑，但当我观察数学史之时，我看到的是一连串不合逻辑的跳跃、不可能的巧合，还有大自然的玩笑。大自然所开的最深刻的玩笑里，一个例子是薛定谔（Erwin Schrödinger）在 1926 年发明波动力学时，在他的波方程里加入的 -1 的平方根。薛定谔是飞鸟型的学者，他的出发点在于把力学与光学统一起来。在他之前一百年，汉米尔顿（William Hamilton）藉由使用相同的数学来描述光线和古典粒子的路径，已经将古典力学和几何光学统一起来了。薛定谔的想法是把这个统一架构推广到波动光学和波动力学。当时已经有波动光学了，但是波动力学还不存在，薛定谔必须发明波动力学，才能完成这项统一事业。一开始，他以波动光学为蓝本，写下力学粒子的微分方程，但是这方程完全不合理 —— 他的式子像是在连续介质中的热传导方程。从热传导看不出和粒子的力学有任何关联。薛定谔的想法似乎掉进了死胡同。然后，惊喜就来了。薛定谔把 -1 的平方根放进式子里，突然之间一切都合理了。突然之间，式子变成了波方程，而不是热传导方程。而且薛定谔很高兴地发现，方程的解对应到波尔（Bohr）原子模型的量子化轨道。

结果，薛定谔方程正确描述了我们已知的原子的一切行为，它是所有化学和大部分物理学的基础。式子中的 -1 的平方根意味着大自然是以复数、而非实数来运作。此一发现完全出乎薛定谔的意料，也出乎众人的意料。据薛定谔说，他十四岁的女性朋友容格尔（Itha Junger）当时对他说：“嘿，一开始时连你也没想到，它会得出那么多合理的东西吧！” 整个十九世纪，从阿贝尔（Niels Abel）到黎曼（Georg Riemann）、魏尔斯特拉斯（Karl Weierstrass）等数学家已经发展出非常精采的复变函数论。他们发现当把函数论从实数扩展到复数时，理论变得远远更深刻，威力也更大。但他们始终把复数看成是人为建构的，是由数学家发明出来，作为现实世界的一种有用且优雅的抽象。他们绝不会想到，这个人为发明的数系其实正是原子运动的基础。他们绝对料想不到，大自然早在他们之前就运用虚数了。

大自然的另一个玩笑是量子力学精确的线性性质，意思是：任何物理对象的可能状态，构成了一个线性空间。在量子力学发明之前，古典力学总是非线性的，线性模型只是逼近的成立。但在量子力学之后，大自然突然变成线性的。这对数学有着深远影响。十九世纪时，李（Sophus Lie）发展出精微的连续群理论，用以厘清古典动力系统（dynamical system）的行为。当时的数学家和物理学家对李群毫不感兴趣。李群的非线性理论对数学家而言太过复杂，对物理学家而言太过晦涩。李只能抱憾而终。然而五十年之后，人们发现大自然居然是线性的，而李代数的线性表现论（theory of linear representations）正是粒子物理的自然语言。李群和李代数重获新生，成为二十世纪数学的核心主题。

大自然的第三个玩笑是准晶体（quasi-crystals）的存在。十九世纪的晶体研究，已经能完全枚举欧氏空间中所有可能的离散对称群。已证明的定理指出，三维空间中的离散对称群只能包含三阶、四阶和六阶的旋转。然后在 1984 年，准晶体被发现了，从液态金属合金中产生的真实固体，呈现出二十面体群（icosahedral group）的对称，其中包含五阶旋转对称。同时，数学家彭罗斯（Roger Penrose）发现了平面的彭罗斯铺砖。这是用菱形非周期地铺满整个平面，并形成五边形长程序态（pentagonal long-range order）。合金准晶体是二维彭罗斯铺砖的三维类比。在这些发现之后，数学家必须扩大晶体群的理论以包纳准晶体。这是一个仍在进行中的重要研究课题。

铝钯锰合金准晶体之原子模式

准晶体与黎曼假说

大自然的第四个玩笑是准晶体和黎曼 ζ 函数零点之间的行为相似性。数学家对 ζ 函数的零点大感兴趣，因为已知的零点总是落在一条直线上，没有人知道其原因为何。“除了平凡的零点之外，这些零点必定落在一条直线上” 的命题，即是著名的黎曼假说。证明黎曼假说是百余年来众多年轻数学家的梦想。我在此大胆建议：我们或许能用准晶体来证明黎曼假说。在座的各位数学家或许会认为这个提议像是胡闹，在座中的非数学家则可能不感兴趣。但我仍吁请诸位认真考虑。当物理学家西拉德（Leó Szilárd）年轻时，他对摩西十诫很不满意，于是写了一组新的十诫来取代它。西拉德的第二诫是：“你应朝向崇高的目标行事，而不要问能否达到目标。行为是要能成为典型与模范，并非达成目标的手段。” 西拉德亲身实践他自己的信条。他是第一个想像以核能做武器的物理学家，也是率先积极推动禁用核武的物理学家。他的第二诫在此非常适用。证明黎曼假说是一项崇高的目标，我们不必去问是否能在我们手中完成。接下来我要说的是怎样达成这目标的可能提示。在此，我要先以我五十年前、在成为物理学家之前的数学家身份来发言。我会先谈黎曼假说，然后再谈准晶体。

直至最近，纯数世界里有两大未解难题：证明费马最后定理，以及证明黎曼假说。十二年前，我在普林斯顿的同事怀尔斯（Andrew Wiles）最终完成费马最后定理的证明，于是只剩下黎曼假说。怀尔斯证明费马最后定理，并不只是高超的特技表演，它还需要发现和探索新的数学思想领域；这远比费马最后定理本身意义更大，而且影响更深远。黎曼假说的任何证明，很可能也会使我们得到对许多不同数学领域、甚至是物理学领域的更深刻理解。黎曼 ζ 函数和其他类似的 ζ 函数，在数论、动力系统、几何学、函数论，乃至在物理学中处处可见。ζ 函数像是位于一个通往各处的中央车站，证明黎曼假说将可阐明所有这些连系。当我年轻时，我就像所有学习纯数学的认真学生一样，梦想能够证明黎曼假说。当时我有一些模糊的想法，是我觉得可用来证明的。当准晶体在最近被发现后，我的想法变得比较清晰了。我在此提出来，供任何有志赢取菲尔兹奖的年轻数学家参考。

准晶体可以存在于一维、二维或三维空间。从物理学的观点来看，三维准晶体是最有趣的，因为它们就存在于我们的三维世界，可以用实验来研究。从数学的观点来看，一维准晶体远比二维或三维的要有趣得多，因为它们的种类远远更为丰富。准晶体的数学定义是这样的：准晶体是一种离散点质量的分布，且其傅立叶变换是一种离散点频率的分布。或者说得再更简短：准晶体是具有纯粹点谱的纯粹点分布。普通晶体是这个定义的特例，它是具有周期谱的周期分布。

排除掉普通晶体，三维的准晶体只有非常少数几种，每一种都和二十面体群有关。二维准晶体就多得多，大致而言，每一个正多边形就对应到一类准晶体。具有五边形对称的二维准晶体就是著名的彭罗斯平面铺砖。最后，一维准晶体因为不受限于旋转对称，所以具有远远更为丰富的结构。就我所知，目前还没有一维准晶体的完整枚举。已知的是，每一个 PV 数（Pisot-Vijayaraghavan number, PV number）就对应到一种唯一的准晶体。PV 数是大于 1 的实代数整数，它是整系数多项式方程的根，且该式所有其他根的绝对值小于 1，参见 [1]。PV 数的数目无穷多，而且构成一种独特的拓朴结构。由所有一维准晶体所构成的集合，其结构至少与所有 PV 数所构成的集合一样丰富，甚至还远胜过后者。关于这一点还不确定，或许正有一宇宙和 PV 数无关的一维准晶体等待我们去发现。

接下来要谈到一维准晶体和黎曼假说的关系了。假如黎曼假说成立，那么根据定义，ζ 函数的零点形成一个一维准晶体。它们构成直线上的点质量分布，而它们的傅立叶变换同样也是点质量分布，变换后的点位于每一个质数或其自然幂次的自然对数值上。我的朋友欧利兹柯（Andrew Odlyzko）曾针对 ζ 函数零点的傅立叶变换，发表了一篇优美的电脑计算 [6]。他的计算正显示了所预期的傅立叶变换的结构，唯有在每个质数或其自然幂次的自然对数值会有尖锐的不连续，其他地方则没有。

我的提议如下。我们暂且假装不知道黎曼假说是否正确，然后从另一头来处理这个问题。我们先试着进行一维准晶体的完全枚举和分类，也就是说，我们对所有具备离散点谱的点分布，进行枚举和分类。对新品种的物体做搜集和分类，是最典型的培根式活动，非常适合青蛙型的数学家。然后我们将发现已经很熟悉的 PV 数准晶体，以及各式各样的其他准晶体，有的已知、有的未知。在众多的准晶体里，我们搜寻对应到黎曼 ζ 函数的准晶体，此外还有每个与黎曼 ζ 函数类似的 ζ 函数，也各有一个对应的准晶体。如果在我们的名单中找到一个准晶体，其性质符合黎曼 ζ 函数的零点，那么我们就证明了黎曼假说，而且可以等着菲尔兹奖的通知电话。

这当然只是异想天开。一维准晶体的分类问题极其困难，可能至少和怀尔斯花了七年时间去钻研的那些问题一样困难。但如果我们才取培根式的观点，数学史就是一代代全然无知的初生之犊，去解决恐怖难题的历程。准晶体的分类是值得努力的目标，而且甚至可能做得到。这种难度的问题不是像我这样的老人能解的，我将它留给在座的青蛙型年轻学者当习题。

贝西柯维契

再来我要介绍几位我所认识的飞鸟型和青蛙型的著名学者。我是在 1941 年进剑桥大学念书的，而且非常幸运，我的导师是俄国数学家贝西柯维契（Abram Samoilovich Besicovitch）。因为当时正值第二次世界大战，剑桥的学生人数很少，研究生更是寥寥无几。所以虽然我年仅 17 岁，而贝西柯维契已是知名教授，他仍对我付出相当多的时间与关注，后来我们成为毕生的好友。他树立了我研究和思考数学的风格。他教的测度论和积分课非常精采，当我们嘲笑那惨遭他蹂躏的英语时，他只回报以和蔼的微笑。我记得只有一次，因为被我们的大笑搞得有点恼怒，他停了一会儿不出声，然后说：“各位先生，五千万的英国人说着你们那种英语，但是有一亿五千万的俄国人说的是我这种英语。”

贝西柯维契是青蛙型学者，他在年轻时即因为解决基本平面几何里的挂谷问题（Kakeya problem）而成名。挂谷问题是这样的：一条长度为 1 的线段在平面上自由移动并同时做旋转，当线段旋转了 360 度时，所扫过区域的最小面积为何？这问题是日本数学家挂谷宗一于 1917 年提出的，其后十年成为一道著名的待解难题。美国当时的数学界领袖柏克霍夫（George Birkhoff）公开宣称，挂谷问题可以和地图着色的四色问题并列为当前最特出的未解问题。当时的人大多相信最小面积是 π/8，也就是三尖内摆线（3-cusped hypocycloid）的面积。三尖内摆线是一条有三个尖的美丽曲线，它是当一个半径为 1/4 的小圆，在一个半径为 3/4 的大圆内贴着大圆圆周滚动时，小圆圆周上的一点所画出的轨迹。

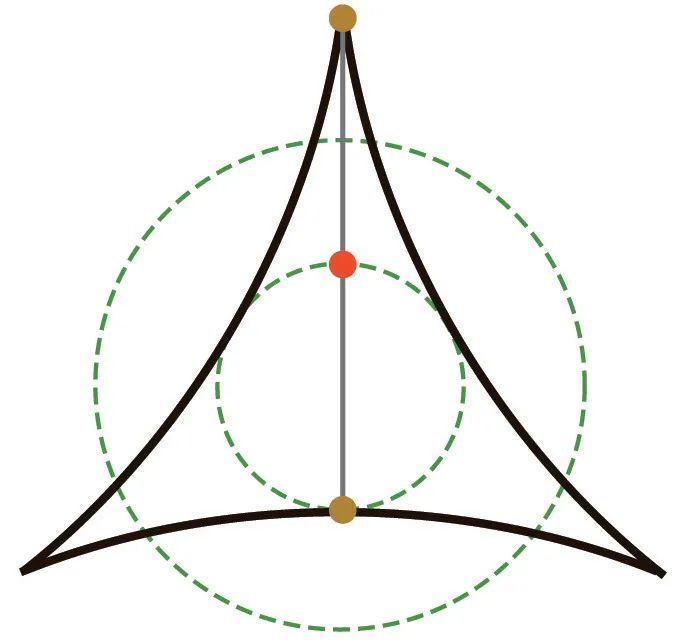
三尖内摆线（Claudio Rocchini 原制，本刊重制）

把长度为 1 的线段置于前述三尖内摆线内、且两端点位于内摆线上，当线段转动时，除了两端点维持在内摆线上之外，必定会有一点与内摆线相切。线段转动的同时永远有三点落在内摆线上，这幅景象非常优雅，使得大多数的人都相信它必定是最小面积。然后出乎所有人的预料，贝西科维契证明了线段移动并旋转所扫过的面积，可以小于任意的正数。

其实早在 1920 年、挂谷问题还不为人所熟知时，贝西科维契即已提出了解答，当时他甚至不知道挂谷宗一提出了这个问题。1920 年时，他在流传不广的《佩尔姆物理与数学学会期刊》（Journal of the Perm Physics and Mathematics Society）上，以俄文发表了解答。佩尔姆位于莫斯科以东 1100 公里，它的大学在俄国大革命后，成为许多杰出数学家的临时避难所。这份期刊出版了两卷，然后就在革命与内战的动荡之中夭折。在俄国之外，这份期刊不仅鲜为人知，而且难以取得。贝西科维契在 1925 年离开俄国，抵达哥本哈根后，才得知他五年前解出的题目是出名的挂谷问题。于是他又再写出解答，这次是以英文发表在德国的《数学期刊》（Mathematische Zeitschrift）上。原始形式的挂谷问题是标准的青蛙型问题 —— 题目很具体，而且和其他数学没什么关联。贝西科维契给出了优雅、深刻的解答，阐明了这个题目其实连系到关于平面点集结构的一般定理。

最能完美展现贝西科维契风格的是发表在德国的《数学年刊》（Mathematische Annalen）上，以 “论线性可测平面点集的基本几何性质”（On the fundamental geometric properties of linearly measurable plane sets of points）为题的三篇经典论文（分别于 1928、1938、1939 年刊载）。他在这三篇论文里证明了平面上每个线性可测集，都可分成一个正则的和一个非正则的部分。其中，正则的部分几乎处处都有切线，而非正则的部分则几乎在所有方向投影的测度皆为零。大致来说，正则部分看起来像连续曲线的组合，而非正则部分看起来一点儿都不像连续曲线。非正则部分的存在及其性质，和贝西科维契如何解决挂谷问题有关。他给我的一个研究题目是把更高维空间里的可测集，分成正则和非正则两部分。我在这问题上毫无进展，但是他的风格却永远铭刻在我心中。贝西科维契的风格像是建筑。他用简单的元素，建造出精致复杂、通常是层级分明的建筑物；然后当建筑物完成后，又用简单的论证将这完成的结构引导至出乎意料的结论。贝西科维契的每个证明都是细心构筑的艺术品，一如巴赫的赋格曲。

魏尔

在我受业于贝西科维契之后过了几年，我来到普林斯顿，并结识了魏尔（Hermann Weyl）。如果说贝西科维契是典型的青蛙，魏尔就是典型的飞鸟。在魏尔从普林斯顿高等研究院退休、回到苏黎士老家之前，我很幸运地和他有一年的共事时间。他对我印象很好，因为那一年我在美国的《数学年刊》（Annals of Mathematics）发表了数论的论文，在《物理评论》（Physical Review）发表了量子辐射理论的论文。魏尔是当时世上少数几个能够同时悠游于这两个领域的人之一。他欢迎我来到研究院，期望我能和他一样成为飞鸟。我令他失望了，我仍固执地当一只蛙。虽然我探索了各式各样的主题，但我一次只能做一个题目，没去找出它们之间的关连。对我而言，数论和量子论是两个不同的世界，各自有其优美之处。我并未像魏尔那样，试图从中找到大自然宏伟设计的线索。

魏尔对量子辐射理论的最大贡献是他发明了规范场（gauge field）。规范场理论的发展有一段有趣的历史。魏尔在 1918 年，为了统一广义相对论和电磁理论，作为一种古典的场而发明了它。[7] 因为这种场是关于长度测量的不可积性，所以他将之命名为 “规范场”。他的统一理论立即被爱因斯坦公开否决。遭到从天庭发出的雷霆一击之后，魏尔并未放弃他的理论，而是转而研究其他课题。他的理论没有可供检验的实验结果。到了 1929 年，当其他人发明了量子力学之后，魏尔才明白他的规范场放在量子世界里，会远比在古典世界更为适切。[8] 要把古典规范场改成量子规范场，只需要把实数改成复数就行了。在量子力学里，每个电荷量子携带了一个具相位的复数波函数，而规范场就是关于其相位的不可积性的测量。于是规范场就和电磁势精确地等同起来，而电荷守恆定律也就是规范场论的局部相位不变量的结果。

魏尔在退休回到苏黎士的四年后辞世。我为他写了一篇追悼文刊载在《自然》（Nature）期刊上 [3]，其中写道：“在二十世纪展开研究生涯的数学家里，魏尔是唯一能在最多不同领域都做出重大贡献的一位。他卓然而立，足以和十九世纪最后的两大数学通才，希尔伯特和庞加莱相比肩。当他在世时，他是纯数学和理论物理齐头并进、紧密连系的活生生表征。如今他去世，这连结也就断了，而我们希望直接使用创造性的数学想像来理解物理世界的企图，也暂时告一段落。” 我哀悼他的去世，但无意追寻他的梦想。我很乐于见到纯数和物理的发展分道扬镳。

悼文的结尾描写的是魏尔人性的一面：“魏尔的性格特点是，美学品味主导了他对一切学识的思考。他曾半开玩笑地对我说：‘我的研究永远试图将真与美结合；但若两者只能择其一，我选择的通常是美。’这句话完美地概括了他的人格，显示出他深深相信大自然最终极的和谐，因而自然律必然是以数学上优美的形式表现出来。这同时也显示了他体认到人的脆弱，再加上他的幽默，使得他不至流于浮夸。魏尔留在我们这些普林斯顿朋友心中的，会是去年四月他在高等研究院春季舞会时的模样 —— 心情很好的大个子，玩得很愉快；他兴高采烈、脚步轻快，完全看不出已有六十九岁。”

魏尔去世后的五十年是实验物理和观测天文学的黄金年代，是搜集事实的培根式旅人、探索居处周遭小片湿地的蛙儿的黄金年代。在这五十年里，关于各式各样的宇宙结构以及各式各样的粒子和交互作用，青蛙们累积了详尽的知识。随着物理学家持续探索新领域的同时，宇宙也变得更复杂。探险家发现的不是以魏尔的数学展现出简洁与优美的宏大设计，而是像夸克、γ 射线爆发之类的奇怪物体，像超对称、多重宇宙之类的奇怪观念。同时，由于探讨混沌现象及其他各种由电脑而开启的新领域，数学同样也变得更复杂。数学家发现可计算性（computability）的核心之谜，是一个可以表成 P ≠ NP 的猜想。这个猜想断言，有些数学问题若以个别案例来处理，可以迅速解决，但却没有适用于所有情形的快速算则。这类问题最有名的例子是旅行推销员问题：有一个推销员要到好几个城市，若任两城之间的距离已知，试找出他旅行的最短路径。所有专家都相信这个猜想是对的，也相信旅行推销员问题是一个 NP 但不是 P 的问题，但大家对于如何证明它却没有丝毫头绪。在魏尔的十九世纪数学世界里，这个问题甚至是没办法表述的。

杨振宁

对飞鸟型学者来说，最近五十年是一段艰苦岁月。但即使岁月艰苦，仍然有事情可做，而飞鸟们也仍奋发从事研究。在魏尔离开普林斯顿后不久，杨振宁从芝加哥过来，搬进魏尔的旧宅。杨振宁接替魏尔的位子，成为我们这一代物理学家领头的飞鸟。在魏尔仍在世时，杨振宁和他的学生米尔斯（Robert Mills）发现了非交换规范场的杨 - 米尔斯理论，这是魏尔的规范场极其优雅的推广 [11]。魏尔的规范场是一种古典量，满足乘法交换律。杨 - 米尔斯理论的规范场则是不可交换的三元组。它们满足量子力学自旋三个分量的交换规则，是最简单的非交换李代数A2的生成元。这理论后来又得到推广，使得其规范场可以是任何有限维李代数的生成元。有了这个推广之后，杨 - 米尔斯规范场论提供了可解释所有已知粒子和交互作用的模型架构，这模型现在称为粒子物理的标准模型。杨振宁又论证，只要让克里斯多福三标数符号（Christoffel three-index symbol）扮演规范场的角色，则爱因斯坦的重力理论也符合相同的架构，又再为这理论添上一笔 [10]。

魏尔在 1955 年为庆祝他的七十寿辰而选编的论文集里，替他的 1918 年论文加写了评注，其中表达了他对规范场理论的最终想法 [12]：“支持我理论的最强论证似乎是这样的：规范不变性与电荷守恆的关系，正如同时空坐标不变性与能量、动量守恆的关系。”（戴森自译）三十年之后，杨振宁在苏黎士纪念魏尔的百岁诞辰时，在演讲 [12] 中也引用了这句话，以证明魏尔是如何专心致志于以规范不变性作为物理学统摄原理的想法。他继续说道：“由于理论和实验的进展，人们现已清楚地认识到，对称性、李群和规范不变性在确定物理世界的基本力时，起着决定性的作用。我把这个原则称为对称性支配交互作用。” 对称性支配交互作用的理念，是杨振宁对魏尔那句评语的推广。魏尔观察到，规范不变性与物理守恆定律密切相关，但因为他只知道可交换场的规范不变性，所以他的理论没办法再往前推展。杨振宁引入非交换规范场，于是建立起远远更强的连系。藉由非交换规范场生成非平凡的李代数，场之间交互作用的可能形式就变成唯一，所以对称性支配了交互作用。这个想法是杨振宁对物理学最伟大的贡献。这是飞鸟才能有的贡献，因为他们飞翔的高度远超过我们大多数人所在的、由枝节问题所构成的雨林之上。

马宁

另一位令我深怀敬意的飞鸟型学者是俄国数学家马宁（Yuri Manin），他最近出版了一本精采的文集，书名是《作为隐喻的数学》（Mathematics as Metaphor）[5]。这本书是以俄文在莫斯科出版，英文版则是由美国数学学会出版。我为英文版写了一篇序，请容我在此念一段序文的话：

作为隐喻的数学是飞鸟型学者极佳的口号。它意味着数学中最深刻的概念是那些能够连结两个理念世界的。17 世纪时，笛卡儿以坐标的概念，把代数和几何这两个相异世界连结起来。牛顿用流数、也就是现在称为微积分的概念，把几何和力学的世界连结起来。在 19 世纪，布尔（George Boole）用符号逻辑的概念把逻辑和代数的世界连结起来，而黎曼用黎曼面的概念把几何和分析学的世界连结起来。坐标、流数、符号逻辑和黎曼面都是隐喻，把字词的意义从熟悉的脉络延伸到陌生的脉络。马宁认为数学的未来是去探索那些已经看得见、但尚未被理解的隐喻。这里头最深刻的隐喻是数论和物理学在结构上的相似性。他在这两个领域都隐约窥见了相彷佛的概念，亦即将连续和离散连结起来的对称性。他期望能看到他称之为数学的量子化的统一。

马宁不同意培根式的故事情节 —— 当希尔伯特于 1900 年的巴黎世界数学家大会上提出他著名的 23 个未解问题时，他也就设定了 20 世纪数学的走向。根据马宁的看法，希尔伯特的问题反而让人从数学的核心主题分心。他认为数学的重要进展是来自于研究纲领，而非来自于问题。问题往往是以新方法运用旧观念而得以解答。研究纲领才是培育新观念的摇篮。他认为，试图以更抽象的语言重写整个数学的布巴基纲领，是二十世纪许多新观念的源头。而试图统一数论与几何的朗兰兹纲领，则很可能蕴育出二十一世纪的新观念。解出著名数学难题的人或许能赢得大奖，但开创新纲领的人才是真正的拓荒者。

英文版的《作为隐喻的数学》比俄文版少了十章，因为美国数学学会认为英文读者不会对这些章节有兴趣。这种省略所造成的遗憾有两重。其一、英文版读者所看到的，只是删节过的马宁观点，而他在数学之外的广泛涉猎，在数学家里是极罕见的。其二、我们看到的，是被删节过的俄罗斯文化景观；在俄国，各领域间的分野并不像英语文化圈那样泾渭分明，数学家和历史学者、艺术家、诗人等的接触更为密切。

冯诺曼

二十世纪数学的另一个重要人物是冯诺曼（John von Neumann）。冯诺曼是青蛙型学者，运用他极其高超的技巧解决了数学和物理里许多领域的问题。他一开始研究的是数学基础，提出了第一组令人满意的集合论公设，避免了康托在处理无穷集和无穷大数时所遇到的逻辑悖论。数年后，冯诺曼的朋友、飞鸟型学者的哥德尔（Kurt Gödel）运用他的公设证明了数学中存在无法判定的命题。哥德尔的定理赋予飞鸟型学者新的数学视野。后此之后，数学不再是用唯一一种真理概念维系起来的单一建筑物，而是具有各种公设系统以及各种真理概念的建筑群。哥德尔证明了数学是无法穷尽的。不论选择哪一组公设作为基础，数学飞鸟们总是能找到这些公设无法回答的问题。

冯诺曼接着转而研究量子力学的基础。为了赋予量子力学一个稳固的数学基础，他创造出非常精采的算子环（rings of operators）理论。每一个可观测量都由一个线性算子来代表，而量子行为的特质都由算子的代数性质忠实地表现出来。就像牛顿发明了微积分以描述古典力学，冯诺曼则是发明了算子环以描述量子力学。

冯诺曼还在其他几个领域做出了基础性的贡献，特别是博弈论和电脑的设计。冯诺曼的最后十年，深深地沉浸在电脑之中。他对电脑的兴趣强烈到不只是研究电脑的设计，而且还用真正的硬体和软体造出一部电脑，并且用它来做科学研究。我仍清楚记得冯诺曼在高等研究院里，刚开始进行电脑计划时的景象。那时他的科学兴趣主要有两项：氢弹和气象学。他在晚上用电脑做氢弹计算，白天则做气象学。白天待在电脑馆的人大多是气象学家，他们的负责人是查尔尼（Jule Charney）。查尔尼是真正的气象学家，在面对变幻莫测的天气时，能适度地保持谦虚，而且也怀疑电脑真的能解开天气之谜。冯诺曼既没那么谦虚，也没那么存疑。我听过一场冯诺曼谈论他的研究目标的演讲。他一如既往，言谈中充满自信。他说：“电脑将能让我们把任一时刻的大气分成稳定区域和不稳定区域。对于稳定区域，我们可以预测；对于不稳定区域，我们可以控制。” 冯诺曼相信任何不稳定区域，都可藉由审慎施加的小幅扰动力量加以推动，使其移往我们希望的任何方向。实施这种小幅扰动的是一群载着制烟设备的机队。这些飞机飞到扰动最有效的地方，藉由烟雾来吸收阳光、提高或降低温度。尤其是，对于即将形成飓风的区域，只要我们能及早确定不稳定处的位置，然后冷却该地的空气，即可阻止其温度上昇产生气旋，如此也就消除了飓风。

冯诺曼的演讲是在 1950 年，当时他宣称只要再十年，电脑的运算能力就足以鉴别大气中的稳定和不稳定区域。一旦能做精确鉴别，那么只要再花一点时间，我们就能控制天气。他预估到了 1960 年代，实际控制天气会是很平常的例行公事。冯诺曼当然错了。他之所以犯错，是因为他不知道混沌（chaos）。我们现在知道，当大气的流动是局部不稳定时，它通常是混沌的。“混沌” 这个词指的是，初始状态很接近的两个运动，会随时间推移而产生指数性的差距。如果一个运动是混沌的，它会变得无法预测；小幅扰动并不能让它变成可预测的稳定运动，通常只是把它变成另一个同样无法预测的混沌运动。所以冯诺曼控制天气的策略失败了。他虽然是一位大数学家，但终究只是个平庸的气象学家。

劳伦兹（Edward Lorenz）在 1963 年发现，气象学方程的解通常是混沌的，那时冯诺曼去世已六年。劳伦兹是气象学家，一般公认他是混沌的发现者。他发现气象中的混沌现象，并赋予其现代名称。但其实早在 1943 年，我就在剑桥的一场演讲里听过数学家卡特莱特（Mary Cartwright，她在 1998 年以 97 岁的高龄辞世）描述相同的现象，这比劳伦兹的发现还早二十年。虽然她用的名称不同，但现象是相同的。她是在求解描述非线性放大器振荡的凡德波尔方程（Van der Pol equation）时发现它们的 [2]。第二次世界大战时，因为在早期雷达系统里是由非线性放大器负责输送功率给发送器，所以凡德波尔方程非常重要。当时发送器的行为常出错，英国空军认为厂商制造的放大器有瑕疵，他们请卡特莱特查看这个问题。她查明了问题不是出在制造商，而是凡德波尔方程。凡德波尔方程的解正是空军所抱怨的混沌行为。我在聆听冯诺曼的气象控制演讲之前七年，就听过卡特莱特讲述混沌，但我没有足够的远见能看出其中关连。我从不曾想过，凡德波尔方程频出岔错的行为，或许和气象有相似之处。如果我是鸟而不是蛙，我或许能看出其中关连，因而能帮冯诺曼省去很多工夫。如果他在 1950 年就知道混沌，他或许就会深刻地思考它，然后在 1954 年时，对这题目发表些重要的洞察。

冯诺曼的晚年陷入了某种困境。因为他其实是青蛙型学者，但每个人都期待他像鸟一样高飞。1954 年时，世界数学家大会在阿姆斯特丹举行。数学家大会每四年举行一次，能受邀在开幕当天演讲是莫大的荣誉。阿姆斯特丹大会的筹办者邀请冯诺曼做全会演讲，期望他能重演希尔伯特 1900 年在巴黎大会上的历史性一幕。就像希尔伯特提出了一系列待解的问题引导二十世纪前半期的数学发展，他们希望冯诺曼能为二十世纪的后半期提出一份清单。冯诺曼的演讲题目列在大会程序册上：“数学的未解问题（筹备委员会邀请演讲）” 。大会结束后出版论文集，收入所有的演讲稿，唯一的例外就是这一场。在论文集里，翻到这一页，只会看到冯诺曼的名字和讲题，下面写着：“本场演讲无原稿。”

发生什么事？我知道是怎么回事。因为当时当地 ——1954 年 9 月 2 日星期四，下午三点，阿姆斯特丹音乐会堂（Concertgebouw）的大厅 —— 我就坐在观众席里。大厅里坐满了数学家，全都期待能听到与这个历史性时刻相称的精采演讲。结果它是一场很失败的演讲。冯诺曼大概是几年前就答应要谈数学的未解问题，然后就忘了这件事。因为有太多事情要忙，他就疏忽了演讲的准备工作。然后在最后一刻，当他想起要去阿姆斯特丹谈谈数学时，他从某个抽屉里找出一份尘封已久的 1930 年代讲稿，打算旧稿新用。这讲稿是关于算子环的，它在 1930 年代是既新又时髦的题目。但它和未解问题无关，和未来无关，也和冯诺曼当时最心爱的题目 “电脑” 无关。如果谈的是电脑，他至少应该会有些新鲜、令人兴奋的内容可说。音乐厅里的听众开始骚动起来。有个人用大得足以让所有人都听得见的音量，用德语说：Aufgewärmte Suppe，意思是 “回锅重热的汤”。当年绝大多数数学家的德语能力都足够听懂这个笑话。冯诺曼深感困窘，匆匆结束他的演讲，不等人发问就离开了。

弱混沌

如果冯诺曼在阿姆斯特丹时就知道混沌现象，弱混沌可能会是他提到的一个待解问题。弱混沌问题在五十年后仍未解决。这个问题是要了解，为何混沌运动往往是有范围的，而不会造成剧烈的不稳定。弱混沌的一个典型例子，是太阳系里行星和卫星的轨道运动。人们直到最近才发现这些运动是混沌的。这是一项惊人的发现，因为传统一向认为太阳系是有秩序稳定运动的典范。早在两百年前，数学家拉普拉斯认为他已经证明了太阳系是稳定的，结果拉普拉斯是错的。对轨道所做的精确数值积分明确显示，邻近的轨道会呈指数性发散。混沌在古典力学的世界里，似乎是无所不在的。

因为太阳系的混沌很弱，所以在精确计算长时段积分之前，人们从不曾想过它会有混沌行为。弱混沌意味着邻近的轨道会指数性发散，但不会离开太远。发散一开始呈指数性成长，但之后就一直是有界的。因为行星运动的混沌很弱，太阳系才能维持长达四十亿年之久。虽然行星运动是混沌的，但它们绝不会离开它们的适当位置太远，所以整体系统也不致崩溃。尽管混沌普遍存在，但把太阳系看成是完美钟表机件的拉普拉斯式观点，仍然近乎事实。

我们在气象学里也可看到相同的弱混沌现象。虽然新泽西的天气一向混沌不定，但这混沌有明确的极限。夏季、冬季的天气有时会超乎预期的怡人或酷烈，但我们总能很放心地预期气温不会高于摄氏 45 度或低于零下 30 度，而在印度和明尼苏达州就经常超过这两个极端。并没有哪条物理守恆律禁止新泽西的气温上升到和印度一样高，或降到和明尼苏达一样低。混沌的微弱，对于生命能够长期在地球上存活是很重要的。弱混沌让我们的天气复杂多变，但又不会太过剧烈波动，以致难以生存。我们现在还不明白，混沌为何如此宽待我们。这是在座的青蛙型年轻学者可以带回家的另一个未解问题。我希望你们能解答：为什么在各式各样的动力系统中所观察到的混沌现象，通常都是弱混沌？

混沌这个主题的特色是：丰富的计量资料、无穷无尽的美丽图片，但却缺乏严格的定理。严格的定理是赋予一个主题知识深度和准确性的最佳方式。直到能证出严格的定理，你才算完全理解你的概念是什么意思。在混沌的领域，我只知道一个严格的定理，是由李天岩和约克（Jim Yorke）在 1975 年的一篇叫做 “周期三蕴涵混沌”（Period Three Implies Chaos）[4] 的短篇论文中证明的。这论文是数学文献中一颗不朽的宝石。他们的定理是关于区间上的非线性自我映射。一个点在重复映射后的

位置数列，可以视为是古典粒子的轨道。

一个点如果在 N 次映射后回到原始位置，则称其轨道具有周期 N。在此脉络下，如果轨道偏离所有周期性轨道，则定义其为混沌的。李 - 约克定理说的是：若一映射存在周期为三的轨道，则亦存在有混沌轨道。定理的证明既简单而且不长。对我而言，这定理及其证明比一千张美丽的图片更能阐明混沌的基本性质。它解释了为何混沌无所不在，但它并未解释为何混沌经常是弱的。这任务就留待后人了。我相信，要从基础上理解弱混沌，我们得先能对它证明严格的定理。

弦论学家

再来我想谈一点点弦论。只谈一点点，是因为我对弦论所知很有限。我不曾费力去跟人学习，也不曾自己钻研。但在我任职的普林斯顿高等研究院，我的身边有一群弦论学家，有时我会旁听他们的对话。他们所说的，偶尔我能听懂一些。就我所见，有三件事是很清楚的。首先，他们所做的是第一流的数学。一些顶尖的纯数学家如阿提雅（Michael Atiyah）和辛格（Isadore Singer）都喜欢他们的东西。弦论开启了全新的数学领域，里面有新想法和新问题。最特别的是，它提供了新方法，以解决一些先前无解的老问题。其次，弦论学家认为他们是物理学家，而不是数学家。他们相信弦论描述的是物理世界里实在的东西。第三，至今为止还没有弦论确实关乎物理的任何证明，这个理论还不足以用实验来测试。弦论与其他的物理学分离，活在它自己的世界里。弦论学家竭尽心力去推导可能足堪测试的理论结果，但尚未成功。

我的同事威滕（Edward Witten）、马尔达西纳（Juan Maldacena）和其他建立弦论的人是鸟儿，高高飞翔并眺望远方山岭的广阔景象。而数千名遍布在世界各大学、比较平凡的弦论研究者则像是蛙，鸟儿看到的是远在天边的数学结构，而蛙儿则探讨其细节。弦论令我忧心的问题并不在于科学，而是社会性的。如果你跻身前一千位弦论学家，能够去发现新连结，开拓新方法，那是很棒的事。但如果你是列在第二个一千名、乃至第十个一千名里，那就没那么美妙了。现在散布全球的弦论学家约有一万人【译注：多人指出戴森过度高估了弦论学者的数目】。这对第十个一千名是很不利的处境，甚至对第二个一千名可能也是。潮流或许会突然改变，使得弦论不再热门，然后造成九千名弦论学家丢掉工作。他们所受的训练是非常特定的专长，这会使得他们难以在别的科学领域找到工作机会。

为什么弦论可以吸引那么多年轻人？它的魅力一部分是来自于智识方面─弦论大胆新颖，而且具有优美的数学结构。但另一方面，它的吸引力也是社会性的。弦论可以提供工作，所以它很迷人。为什么会有那么多弦论的工作机会呢？因为它便宜。如果你在资金匮乏的偏远院校掌管物理系，你手上的经费不足以建造现代实验室来做实验物理，但你可以聘请几位弦论学家。所以你提供几个弦论的职缺，然后你就有了一个赶得上时代的物理系了。对于提供工作的系主任，和寻找工作的年轻人，这种诱惑是很强烈的。不管是对年轻学者或对科学的未来，这都是有害的。我并不是认为，即使年轻学者觉得弦论很有趣，我们也要劝阻他们不要去做。我的意思是，我们应该提供他们多种选择，免得他们因为经济需求而去做弦论。

最后再说一下我对弦论前景的猜测。我的猜测不见得正确，我不会幻想自己能预测未来；之所以在此说出我的想法，是为了提供各位一些思考的素材。我想，弦论最终的结果极不可能会是完全成功，或是完全无效。在此，“完全成功” 系指弦论是一个物理学的完整理论，足以解释粒子及其交互作用的所有细节。至于 “完全无效” 意味着，弦论只是一件纯粹数学的美丽作品。我猜弦论会介于完全成功与彻底失败之间。我猜它的情形会和李群理论相似。李在十九世纪时创建李群，以做为古典物理的数学架构。只要物理学依旧是古典的，李群就是一个失败的理论。他们有了解答，却不知道要回答什么问题。直到五十年后，量子革命改变了物理学，于是李代数找到了它的适当位置。若要理解对称性在量子世界里的核心地位，李代数是解答的关键。我预期在五十年或一百年之后，将会发生另一场物理学革命，引入目前毫无迹象的新概念，而这些新概念将赋予弦论新的意义。在此之后，弦论将突然找到它在宇宙中的适当位置，做出关于真实世界的可检验的预测。我得警告各位，这个猜测可能是错的。但它有一项优点，即可以被证伪（falsifiable），根据科学哲学家波普（Karl Popper），证伪性是科学叙述的标志。或许就在明天，日内瓦的大型强子对撞机的实验结果就会摧毁我的预言。

欧洲核子研究组织（CERN ）日内瓦实验室的大型强子对撞机

回到马宁的隐喻

在演讲的最后，我想回到马宁和他的《作为隐喻的数学》。这本书的内容主要是数学，但西方读者可能会惊讶地发现，他能以同样流畅的文笔来谈论其他主题，像是集体潜意识、人类语言的起源、自闭症心理学；以及恶精灵在世界许多文明的神话中所扮演的角色。对他的俄国同胞而言，这种多方面的兴趣与专长毫不令人讶异。俄国知识分子维持了传统俄罗斯知识阶层的傲人传统 —— 科学家、诗人、艺术家和音乐家结合成一个社群。他们今天仍是如此，就如同我们在契诃夫的戏剧中所见到的一样，一群理想主义者因为难以见容于迷信的社会和恣意妄为的政府，而聚集在一起。在俄国，数学家、作曲家和电影制片人可以相互对话，在冬夜的雪地里一起散步，同斟共饮，以及分享彼此的想法。

马宁是飞鸟，他能超越数学领域，而看到更广阔的人类文化地景。他的一项嗜好是探讨瑞士心理学家容格（Carl Jung）所发明的原型理论。根据容格，原型是深植在我们共有的集体潜意识里的心理意象。原型所携带的强烈情感，是人们集体的欢乐与悲伤，在被遗忘后所留下来的遗迹。马宁认为，即使我们不接受容格的理论为真，也可从中得到很多启发。

早在三十多年前，法国歌手莫芮利（Monique Morelli）录制了一张由麦柯朗（Pierre Mac Orlan）作词的歌曲唱片。其中一首曲子叫 “死城”（La Ville Morte），它萦迴不去的旋律由莫芮利深沉的女低音唱出，配上手风琴的对位伴奏，描绘出种种情感强烈的意象。当印在纸页上时，这些词句平凡无奇：

走入死城，

我牵着玛歌的手

……

一路踅过墓城，

支着断脚，静默不语，

眼前是未锁的门户，

眼前是不起眼的弹孔，

眼前是众门无言，

垃圾桶遍地哀嚎。

每当聆听这首歌，必定会激起我非常强烈的情绪。我常自问，为何这么简单的歌词却似乎能与某种深层潜意识的记忆发生共鸣，就好像逝去者的灵魂透过莫芮利的音乐在说话。而现在，出乎意料地我在马宁的书中找到了答案。在其中一章，“空城原型”（The Empty City Archetype），马宁描述死城的原型如何从古至今，一次又一次出现在建筑、文学、艺术和电影等创作里。自从某些人开始聚集在城市里，自从另一些人开始聚集成军队，以肆虐和摧毁城市，这个原型就反覆出现。麦柯朗的歌曲说的是很久以前佔领军中的老兵，当他和妻子走过死城的瓦砾灰烬后，他再次听见：

奇魅的号角曲调

遥遥响了一个时辰

在老兵的梦中。

麦柯朗的文字和莫芮利的声音似乎召唤起我们集体潜意识中的一个梦，一个关于老兵在死城中游荡的梦。集体潜意识的概念或许和死城的概念一样，都是神话的。马宁在这一章，描述了这两个或属神话的概念如何相互投射了照亮对方的熹微之光。据他描述，集体潜意识是一股强大的非理性力量，足以将我们拉向死亡和毁灭。死城的原型则是在城市和攻城大军被发明之后，由数以百计被毁城市的哀愁凝炼而成。若要逃脱疯狂的集体潜意识，唯一的途径是以希望与理性为基础，建立起清明的集体意识。创造这样的集体意识，便是我们当代文明所面临的重大任务。

延伸阅读

1. 多人，Letters to Editor, Notices of the AMS56(2009), no. 6. 读者对戴森文章的回应，以及戴森对回应的回应。

2. John Baez,Quasicrystals and the Riemann Hypothesis, The n-Category Café Blog. 探讨戴森对黎曼假说与一维准晶体关系论点的可能诠释。http://golem.ph.utexas.edu/category/2013/06/quasicrystals_and_the_riemann.html

3. Thomas Lin,A ‘Rebel’ without a Ph.D., Quanta, March 26, 2014, Simons Foundation. 戴森在本文中追忆他的师友，而这篇访谈的主角则是他本人，两文可互参。

http://www.simonsfoundation.org/quanta/20140326-a-rebel-without-a-ph-d/

4. A. S. Besicovitch,The Kakeya Problem, The American Mathematical Monthly70(1963), no. 7, MAA. 贝西柯维契后来又再写了一篇普及版的挂谷问题介绍。这篇文章在网路也能找到。

参考文献

[1] M.J. Bertin et al., Pisot and Salem Numbers, Birkhäuser Verlag, Basel, 1992.

[2] M.L. Cartwright and J.E. Littlewood,On nonlinear differential equations of the second order, I, Jour. London Math. Soc.20(1945), 180-189.

[3] F. Dyson,Prof. Hermann Weyl, For. Mem. R.S., Nature177(1956), 457-458.

[4] T.-Y. Li and J.A. Yorke,Period three implies chaos, Amer. Math. Monthly82(1975), 985-992.

[5] Yu.I. Manin, Mathematics as Metaphor: Selected Essays, American Mathematical Society, Providence, Rhode Island, 2007. [The Russian version is: Yu.I. Manin, Matematika kak Metafora, Moskva, Izdatyelstvo MTsNMO, 2008.]

[6] A.M. Odlyzko,Primes, quantum chaos and computers, in Number Theory, Proceedings of a Symposium, National Research Council, Washington DC, 1990, pp. 35-46.

[7] H. Weyl,Gravitation und elektrizität, Sitz. König. Preuss. Akad. Wiss.26(1918), 465-480.

[8] H. Weyl, Elektron und gravitation, Zeits. Phys.56(1929), 350-352.

[9] H. Weyl, Selecta, Birkhäuser Verlag, Basel, 1956, p.192.

[10] C.N. Yang,Integral formalism for gauge fields, Phys. Rev. Letters33(1974), 445-447.

[11] C.N. Yang and R.L. Mills, Conservation of isotopic spin and isotopic gauge invariance, Phys. Rev.96(1954), 191-195.

[12] C.N. Yang and R.L. Mills,Hermann Weyl’s contribution to physics, in Hermann Weyl, 1885-1985, (K. Chandrasekharan, ed.), Springer-Verlag, Berlin, 1986, p.19.

修改于 2020 年 03 月 02 日

---

戴森传奇 —— 从数论、QED 到科普写作大师（上）

原创 林开亮 数理人文 2016 年 12 月 15 日 18:23

作者简介：林开亮，首都师范大学数学博士，目前任教于西北农林科技大学理学院。

戴森，摄于 2005 年（维基）

我人生中最重要的三件事，依序是：家庭、朋友和工作。所以我最大的贡献是养育六个儿女，他们都在不同领域事业有成，也都已成家。我自己的工作则没那么重要，而且我身为作家的工作成就，或许还比我作为科学家的成就重要。—— 戴森，2012 年 11 月 21 日致笔者函

戴森（Freeman Dyson）的名字对中国人而言应该不陌生。作为杰出的作家，他拥有广泛的读者，已有多部著作被迻译成中文（参见附录 “戴森至今的科普书籍列表”），其中处女作《宇宙波澜》（Disturbing the Universe）甚至有三个中译本，而邱显正的译本更在 2002 年荣获台湾吴大猷学术基金会颁发的首届 “吴大猷科普著作奖”。想必许多读者都为戴森的文笔所吸引，但对于他作为数学家和物理学家的身份却未必了解。本文将尝试解读这位集科学才能与人文修养于一身的大家。

现年 93 岁的戴森仍笔耕不辍且持续做研究，包括纯数学方面的有趣工作。十多年前，戴森曾应南开大学数学所葛墨林教授之邀访问中国，并游览了北京和古城西安。中国悠久的文化与快速的发展，让他留下深刻的印象，并对中国在世界舞台上将扮演的角色寄予厚望。此点反映在他于 2013 年 7 月 26 日回复给老友杨振宁的邮件中：

你写道，当我们年轻时，研究的重心从欧洲转移到美国。然而此刻我看到了 21 世纪一项最重要的事实，即世界舞台的中心将从美国转移到中国。你可以因为有幸先后为这两大转变做出贡献而骄傲。留给我们儿孙辈的主要任务是，要见证这个转变和平地发生。…… 我常常想起你的美文 “父亲和我” [1]。令尊【注： 杨振宁父亲杨武之是数学家暨数学教育家，1928 年在芝加哥大学代数与数论专家迪克森（L.E. Dickson）指导下获博士学位，是中国传播近代数学的先驱】也必定会为之骄傲。

英才少年

戴森 1923 年 12 月 15 日生于英国。 母亲雅特琪（Mildred L. Atkey）是律师，40 岁生下爱丽丝・戴森（Alice Dyson），43 岁生下戴森，之后一直以社会工作为职。父亲乔治・戴森（George Dyson）是音乐家，曾任教英国历史悠久的温彻斯特公学（Winchester College），后来升任伦敦皇家音乐学院院长。乔治对科学很有兴趣，书架上陈列众多科学书籍，如怀德海（Alfred. N. Whitehead）、 爱丁顿（Arthur Eddington）、金斯（James Jeans）、霍格本（Lancelot Hogben）和霍尔丹（John. B. S. Haldane）的作品。戴森从小就接触科学，但他认为，在成为科学家之前，他早就是作家了，因为他九岁时就创作了一篇科幻小说。这篇未完成的处女作，后来收入通俗文集《从爱神到盖娅》（From Eros to Gaia）中。

（左）凡尔纳。（Félix Nadar 摄）（右）法国画家 Paul D. Philippoteaux 绘製、Charles Laplante 镌刻的《太阳系历险记》插图。场景包括在太空中见到欧洲、俄国、法国；土星和卫星；漂浮的人物。引起 19 世纪读者对外太空的想像与热情。（维基）

戴森小时候非常迷恋凡尔纳（Jules Verne）创作于 1877 年的《太阳系历险记》（Hector Servadac）。他一直以为这是真实故事，日后发现原来 “一切纯属编造” 时非常失望。不过，凡尔纳的科幻风格激发了戴森童年时期的写作。

戴森幼年即展现非凡的数学才能。他在为《科学的面孔》（Faces of Science）[2] 所写的简短自传中讲述了一个故事。当他还小，躺在婴儿床睡午觉。有一天他不想睡，就用计算打发时间。他先算

1+1/2+1/4+1/8+1/16+…

发现最终得数为 2。然后，他又计算

1+1/3+1/9+1/27+1/81+…

发现最终得数为 3/2 。他再计算

1+1/4+1/16+1/64+1/256+…

发现最终得数为 4/3。换句话说，他发现了无穷级数。当时他没有跟任何人说起这个奇妙的经历，觉得这仅仅是他喜欢的一个游戏。

1936 年，戴森通过竞争激烈的考试，升上父亲执教的温彻斯特公学，直至 1941 年毕业。他与隆科希金斯兄弟（Christopher Longuet-Higgins、Michael Longuet-Higgins）、 莱特希尔（James Lighthill）结成 “四人帮”，他们后来都在各自的科学领域拥有卓越的贡献，并皆入选为英国皇家学会会士。克利斯朵夫・隆科希金斯是理论化学家，同时也是音乐认知学家。麦可・隆科希金斯是数学家和海洋学家，曾与几何学家考克斯特（H.S.M. Coxeter）合作过关于均匀多面体的著名论文。莱特希尔是著名的流体力学专家，曾担任狄拉克（Paul Dirac）与霍金（Stephen Hawking）之间的卢卡斯数学讲座教授。

温彻斯特公学不赞成以正式课程逼迫有天赋的孩子提前学习高等数学与科学，认为学生自主学习更好，因而有意放任学生有更多的时间可以自由支配，戴森和其他男孩主要即靠自学。戴森说，“四人帮” 之间相互学习的收获，比从老师那里学到的还要多。

在戴森看来，温彻斯特公学设有极好的评奖机制。学校每年针对各年级举行三次竞赛，优胜者可获得 30 先令，但只能在学校书店里消费。戴森经常在竞赛中获奖，因而拥有自己的藏书。1937 年至 1940 年，他赢得 19 本书。这些书对他的兴趣发展及智力培养具有决定性作用，有些书甚至成为他一生的珍爱。

其中最具影响的几本是：贝尔（Eric T. Bell）的《数学精英》（Men of Mathematics，[3]）、哈代（Godfrey H. Hardy）与莱特（Edward M. Wright）合著的《数论导引》（An Introduction to the Theory of Numbers,[4]）、约斯（Georg Joos）的《理论物理》（Theoretical Physics）和拉马努金（Srinivasa Ramanujan）的《数学论文集》（Collected Papers）。

戴森被贝尔的数学科普书《数学精英》深深吸引。他在 [2] 中曾回忆道：

14 岁时我读了贝尔的《数学精英》，书中记载了许多伟大数学家的传奇故事。贝尔是加州理工学院的数学教授，同时也是极具天赋的作家。他令人信服地向读者介绍了数学界的精英，擅于打动情感敏锐的青少年心弦。贝尔的书造就了整整一代的年轻数学家。尽管书中许多细节与事实不符，但主要情节是真实的。在贝尔笔下，数学家是有血有肉的人，也会做错事，也有瑕疵。数学俨然成了各式各样的人都能涉足的魔法王国。该书传递给年轻读者的资讯是：“如果他们能做到，你为何不能？”

贝尔的书激发了戴森成为数学家的抱负。他甚至兴起这样的梦想─有一天要证明出著名的黎曼假说（Riemann Hypothesis）。

1939 年 9 月 3 日，英国首相张伯伦被迫对希特勒宣战，英国加入二次世界大战。圣诞假期里，为了弄懂爱因斯坦的相对论，戴森开始自修一部较高深的数学书，比雅久（Henry Piaggio）的《微分方程初步》（An Elementary Treatise on Differential Equations），是他当年在学校获得的奖品。戴森担心自己会丧生于战争，那样的话他甚至可能比贝尔书中最悲惨的数学天才伽罗瓦（Évariste Galois）还要悲惨，因为毕竟伽罗瓦在决斗前就已经创造出不朽的数学成就。当时戴森满脑子里只有伽罗瓦决斗前的遗言 “我没时间了，我没时间了。”

母亲箴言

因此，戴森全心投入到数学中，从早上六点到晚上十点，除了中午休息两个小时，每天平均学习长达 14 个小时。虽然戴森自己乐此不疲，却令他的父母很担忧。母亲引用了乔叟（Geoffrey Chaucer）笔下牛津教士的话 “一心专注求学问，无暇他顾出一声”，并警告他，长此以往将要生病甚至损坏大脑。父亲则一再建议他放下书本，一起出门干点农活以暂时放送一下。但戴森置若罔闻，继续沉迷于比雅久的《微分方程初步》中。圣诞假期即将结束时，戴森已完成书中的近 700 道习题，差不多要大功告成了，因此愿意抽空陪母亲一起散步。母亲对此已期盼多时，且早有准备。母亲当时说的话，对戴森产生了深远的影响。我们可从其科学自传《宇宙波澜》引述如下：

我母亲是个律师，对人极感兴趣，她喜欢拉丁诗人和希腊诗人。同我讲话时，她先引用原是非洲奴隶、后来成为最伟大拉丁剧作家的埃福（T. Afer）剧本《自虐者》（The Self-Tormentor）中的一句台词：“我是人，我绝不自异于人类。” 这是她在漫长的一生中，直到 94 岁去世，一直奉为信条的箴言。当我们沿着泥沼和大海之间的堤坝漫步时，她对我说，这句话也应该成为我的信条。她了解我对比雅久抽象美的渴望和热爱，但她要求我，在渴望成为数学家的过程中，不要丢失人的本性。她说：有朝一日你成了大数学家，却醒悟到自己从未有时间交过朋友时，你将追悔莫及。如果你没有妻子和儿女来分享成功的喜悦，那么纵使你证明出黎曼假说，又有什么意义呢？如果你只对数学感兴趣，那么日后你将会感到，数学也变得索然无味，有如苦酒。

诚如戴森在书中所说，“母亲的箴言已经逐渐深刻地印入我的潜意识中，并不时产生意想不到的影响。”

戴森还下功夫读了哈代和莱特的《数论导引》[4]，并尝试证明书中的每一个定理。要知道全书共有 400 多条定理，而戴森当时还不满 14 岁！这本书让戴森兴起对数论的浓厚兴趣，而哈代对戴森长达一生的影响也由此拉开序幕。

除了阅读自己的获奖藏书以外，戴森还与莱特希尔一起读了学校图书馆的另外两本书：怀德海和罗素（Bertrand Russell）的《数学原理》（Principia Mathematica）与约当（Camille Jordan）的《分析教程》（Cours d’Analyse）。这两本书是莱特希尔的意外发现。他们很快判断出，《数学原理》是部失败的作品，而《分析教程》则是打开现代数学殿堂之门的钥匙。他们一直很好奇，《分析教程》这本用法语写成的三卷本大部头高等数学教材，怎么会出现在学校的图书馆里。直到多年后，戴森读到哈代的《一个数学家的辩白》[5] 这本经典著作时，才找到合理的解释。哈代在书中描述《分析教程》一书对他的影响：

我永远忘不了阅读这本伟大著作所带来的惊喜，对与我同时代的许多数学家来说，这是第一个启迪。在阅读它的时候，我第一次了解到数学的真正涵义。此后，我才走上了成为具有健康的数学志向、对数学具有真诚热情和抱负的真正数学家之路。

哈代的感受必定引起了戴森的共鸣。后来戴森才得知，原来哈代在 40 年前也曾就读于温彻斯特公学（哈代在此过得不太愉快，因而很少提及这个著名的母校）。戴森一度猜测，也许正是哈代有意在学校图书馆留下这本书，想 “藏诸名山，传之其人”。后来戴森升上剑桥大学，成了哈代门生，但由于恩师高高在上难以接近，戴森没有勇气找他求证。1947 年哈代去世后，这也成了戴森的一大遗憾。

在公学的最后一个暑期，戴森的高中数学老师杜雷尔（Clement Durell）安排了几何学家佩多（Daniel Pedoe）来专门辅导戴森与莱特希尔。佩多当时是 20 公里外南安普敦大学的助理讲师，他是戴森见到的第一位真正的数学家。佩多后来曾追忆起 17 岁的戴森 (见 [6])：

戴森问我有没有比中学里的无穷级数问题更有趣的东西，我建议他研究将平面内由方程

x2+y2−2px−2qy+r=0

给出的有向圆用三维空间中的点 (p, q, r) 表示的问题。我曾发表了一篇极其深入的论文讨论这个优美的表示。例如，共轴的圆将表示为三维空间中的直线。戴森深受吸引，至今仍然记得那件事。

诚如戴森所说，虽然他没有成为几何学家，却从佩多身上学到了对几何风格的鉴赏力，从而将数学看作一门艺术，而不仅只是科学。

戴森在学校里还结交长他三岁的文艺青年汤普森（Frank Thompson）。汤普森对戴森的影响比校内其他人都要大。他 15 岁就赢得 “学校诗人” 的称号，对诗歌有深厚的感情。对他来说，诗歌不仅是智力上的消遣，且一直都是人们从无法言喻的灵魂深处淬炼出的智慧结晶。身为敏感的诗人，他更关心校外的大千世界，尤其是当时正如火如荼的西班牙内战与即将来临的二次世界大战。戴森自汤普森处首度了解到战争与和平的重大道义问题，不过正如汤普森离开诗歌就不能生活一样，戴森最钟爱的依然是数学。汤普森不幸在二战中牺牲，其英雄事迹被戴森谱写进《宇宙波澜》“诗人之血” 一章。

剑桥大学

1941 年 9 月，戴森与莱特希尔双双进入剑桥大学。由于当时英国处于非常时期，所有大学都尽可能缩短课程，以便学生尽快投入战争。许多学生只学习一年就离校从军，戴森相对幸运，在剑桥听了两年课，1943 年才去服兵役。

当时剑桥大学只剩下年长的教授，数学系有哈代、李托伍德（John Littlewood）、霍奇（William V.D. Hodge）、莫德尔（Louis Mordell）、贝西柯维契（Abram Besicovitch），物理系有狄拉克、爱丁顿、杰弗里斯（Harold Jeffreys）、布拉格（William L. Bragg）。学生很少，在许多课堂上，戴森与莱特希尔就占了听众中的一半，杰弗里斯的流体力学课甚至可怜到只有戴森一名学生。

狄拉克（维基）

这些教授中，以狄拉克最富名气。狄拉克是量子力学的奠基者之一，1930 年出版《量子力学原理》（The Principles of Quantum Mechanics），日后成为物理学的圣经之一。狄拉克授课几乎就是一字不差地照本宣科，这让戴森很失望。这个课程完全缺乏从历史角度看待问题的意识，此外狄拉克也没有教学生如何具体计算。戴森总是在课堂上提问，狄拉克往往需要停顿很久才能答覆他，有一次狄拉克甚至不得不提前下课，以便准备正确的答复。

贝西柯维契（维基）

戴森对哈代与李托伍德的课程非常满意。他注意到这两位著名的数学搭档风格迥异，哈代将数学作为成熟的优美艺术品展现给学生，而李托伍德则将数学作为智力拼搏的过程展示给学生。戴森更喜欢李托伍德的风格。不过，最能引起戴森共鸣的还是贝西柯维契的风格。1993 年，戴森专为三联版《宇宙波澜》写的序言，特别提及贝西柯维契对他的深远影响：

我的科学生涯是以纯数学家开始的，对我思维方式影响最深的老师是俄国数学家贝西柯维契。在我的物理和数学研究风格上，贝西柯维契的痕迹清晰可见。…… 贝西柯维契的风格是建筑式的。他依照层次分明的计划，从简单的数学元素中构造出微妙的建筑结构，而当他的建筑物完成时，整个结构通过简单的论证就引出意想不到的结论。…… 从某种程度上说，每个科学家都是艺术家。作为艺术家，我以数学思想为工具，奉贝西柯维契为楷模。

1943 年自剑桥完成学业后，戴森服役投入战局，为皇家空军处理统计工作。直至 1945 年战争结束，他获得了数学学士学位，但役期还有一年，他被慨允在伦敦的帝国学院教学。战争吞噬了许多年轻的生命，校园萧条，戴森几乎没有教学任务。他的上司查普曼（Sydney Chapman）是著名的数学家和地球物理学家，鼓励他随心所欲做自己想做的事情。戴森于是成了伦敦大学伯贝克学院的数论专家戴文波特（Harold Davenport）讨论班上的常客。与剑桥的哈代、李托伍德、贝西柯维契等形单影只的局面完全不同，戴文波特的身边有一群年轻研究生，研究氛围十分热络。戴森向戴文波特提起他对西格尔猜想（Siegel’s Conjecture）的兴趣，得到极大的鼓励。

数学 vs. 物理

其实当时戴森已有从数学转向物理的念头。之前他读过物理学家海特勒（ Walter Heitler）的专著《辐射的量子理论》（The Quantum Theory of Radiation），该书总结了 1930 年代末理论物理学的状况，并提出解决基本问题的建议，深深吸引了戴森。但戴文波特的友情和他在数学上的激励，令戴森一时犹豫不决。于是戴森决定用西格尔猜想来抉择他的学术命运。如果解决这一猜想，就继续做数学，如果失败，就皈依物理。三个月的艰辛工作之后，戴森认输了。不过他虽然没有完全解决西格尔猜想，但至少取得了部分成功，改进西格尔早先的结果。这个问题最后由德裔英国数学家罗斯（Klaus Roth）给解决了。

1945-1946 年是戴森在数学上的黄金年代。除了在西格尔猜想方面取得部分进展以外，他还对另外两个问题 —— 几何数论中的闵可夫斯基猜想（Minkowski’s Conjecture） 与堆垒数论中的 α-β 猜想 —— 有重要贡献【注：α-β 猜想在 1942 年为曼恩（Henry Mann）证明。闵可夫斯基猜想则至今仍未解决，目前的研究进展可见 http://arxiv.org/pdf/1410.5743v1.pdf】。

1946 年退伍后，戴森凭藉出色的数学成就，成为剑桥三一学院的研究员。他原打算重新学习现代物理，但慢慢意识到，他真正需要的是找一名理论物理学家交谈，以获悉当前尚未解决的重要问题，如此一来，或可凭藉自己的数学功底探探深浅，检视自己是否适合投身物理。幸运的是，查普曼告诉他，在剑桥恰好有他要寻找的人 —— 坎梅尔（Nicholas Kemmer）。

1940 年代的坎梅尔（维基）

坎梅尔曾受教于苏黎世大学的泡利（Wolfgang Pauli）和温策尔（Gregor Wentzel），他将从恩师处习得的量子场论悉心传授给戴森。量子场论主要是狄拉克、海森堡（Werner Heisenberg）、泡利、费米（Enrico Fermi）的研究成果，其行家大多是欧洲人。当时懂得量子场论的人寥寥无几，有关量子场论的书籍只有一本问世，作者就是温策尔。戴森从坎梅尔那里了解到其重要性，掌握了一手绝技，这对他日后从事物理研究有莫大的帮助。坎梅尔极有耐心地指导戴森，为他详细解释温策尔书中的要点，让戴森理解并接受，量子场论提供了一种以自洽数学架构描述大自然的关键。戴森一生阅人无数，他推崇坎梅尔是平生所见最无私的科学家。

虽然有坎梅尔的指点，但有更多因素促使戴森离开剑桥，前往美国开始新生活。戴森在卡文迪什实验室邂逅了流体力学专家泰勒（Geoffrey Taylor），二战期间泰勒曾在美国的洛斯阿拉莫斯（Los Alamos）国家实验室工作。戴森向他打听美国哪些地方适合做物理，泰勒立即回答：“噢，你应该投奔到康奈尔大学贝特（Hans Bethe）门下，那是战后洛斯阿拉莫斯实验室所有聪明人向往的地方。” 在泰勒的热心推荐下，1947 年戴森隻身前往美国。

贝特摄于洛斯阿拉莫斯（维基）

有趣的是，就在戴森决定从数学转向物理之际，剑桥的另一个人却决定从物理转向数学，即后来成为大数学家的黑利希钱德拉（Harish-Chandra）。黑利希钱德拉是印度人，起初追随狄拉克研读博士，因为缺乏狄拉克对物理那种神祕的 “第六感”，最终离开物理界。黑利希钱德拉后来随导师狄拉克一起访问美国普林斯顿高等研究院时，遇到了戴森。他向戴森说道：“我为了数学而离开物理学。我发现物理学乱七八糟、不严格、难以捉摸。” 戴森则回答：“恰恰出于同样的原因，我离开数学而投入物理学的怀抱。”

成功转行

1947 年 9 月，戴森入学康奈尔师从贝特。他立即发现自己适得其所─整个康奈尔大学，居然只有他懂得量子场论。量子场论是一个成熟的数学构造，当初欧洲学者创造这个理论时，多是基于对数学美学的考虑，而不是解释实验方面的成功，多数信奉实用主义的美国物理学家因此不愿费力去学习。后来他们发现，许多实验需得运用量子场论才能解释，学习量子场论因而成为必要条件。戴森的到来恰逢其时。他一边跟随指导老师贝特与聪明的年轻教员费曼（Richard Feynman）学习物理，一边也教他们如何处理量子场论的问题。戴森带来的技巧可以计算出原子碰撞过程，得出的资料又能为实验验证，因此迅即获得师友的青睐。

在那个年代，贝特关心的是量子电动力学（quantum electrodynamics，QED）中的问题，该理论致力于精确描述原子和电子如何发射和吸收光子。如今回顾起来或许有些不可思议，因为在量子力学诞生 20 多年后的 1947 年，人们对最简单和最基本的粒子、氢原子和光量子，竟还没有精确的理论。不过尽管如此，当时也出现突破性进展：物理学家兰姆（Willis Lamb）同年测出了所谓的 “兰姆位移”，引起同行们的高度关注。同年 6 月，美国科学院在纽约谢尔特岛专门召开会议，讨论兰姆位移及相关问题，是科学史上的盛事，虽然与会者仅有 24 位，但都是一流人物。正是在这次会议上，诞生了重整化（renormalization）的想法。贝特就是利用这一想法，在会后返回康奈尔的火车上粗略计算出兰姆位移。他给戴森的题目，就是深入探究重整化，给出严格的处理。这在当时是最热门、最前沿的理论问题。

1948-1949 年，戴森遵循贝特的建议，前往普林斯顿高等研究院访问一年。这是戴森科学生涯中最关键的一年。那一年，年仅 25 岁的戴森做出了他在物理学上最重要的贡献 —— 量子电动力学的重整化。一年之间，他从无名小卒一跃成为物理学界闪亮的新星。他成功转行了！

当时美国物理学界研究重整化的活跃份子有两个物理学家─康奈尔的费曼与哈佛的史温格（Julian Schwinger）。两人都是物理奇才，但品味与风格大相径庭。1948 年，凭藉出色的数学天分与社交能力，戴森直接从费曼与史温格身上，学到他们各自对量子电动力学的处理方法，并完美吸取两种方法的优点，从数学角度为量子电动力学重整化提出自洽表述。在《宇宙波澜》 第六章中，他曾回忆起灵光一闪、豁然开朗的美妙瞬间：

第三天，当巴士徐徐驶过内布拉斯加的时候，奇迹发生了 —— 我搁置两周没有思考的物理，此刻排山倒海一股脑儿地涌进我的脑海里。费曼的图像和史温格的方程式，在我脑中自动地一一对应，无与伦比地清晰。我生平第一次将这两个观点连接在一起。有一两个小时里，我将那些片段不停地重组再重组，忽然领悟到，他们其实可以彼此配合得天衣无缝。虽然手边没有笔和纸，但一切都是那么清晰，根本不需要记录下来。费曼和史温格其实是从不同角度看待同一个思想，若将两人的方法结合起来，就可以得到一个兼顾史温格数学上的严谨，以及费曼应用上灵活的，理想的量子电动力学理论。

1957 年代的杨振宁（维基）

返回普林斯顿后，戴森透过奥本海默（J. Robert Oppenheimer），了解到日本物理学家朝永振一郎（Sinichiro Tomonaga）的早期贡献，其后精心完成论文 “朝永、史温格和费曼的辐射理论”（The radiation theories of Tomonaga, Schwinger, and Feynman），日后影响深远。此论文标题或多或少留给读者的印象是 —— 理论是属于朝永、史温格和费曼三人的，戴森只是做了简单的整合。然而事实并非如此简单，诺贝尔物理学奖得主杨振宁对戴森的工作即有高度评价（见 [7]）：

费曼（左） 、史温格（中） 、朝永振一郎（右）（Nobel Foundation）

重整化纲领是物理学的伟大发展。这个理论的主要缔造者是朝永、史温格、费曼和戴森。1965 年诺贝尔物理学奖授予朝永、史温格和费曼时，我就认为，诺贝尔委员会没有一併认可戴森的贡献，乃铸成了大错。直到今天，我仍然这么认为。朝永、史温格和费曼并没有完成重整化纲领，因为他们只做了低阶的计算。只有戴森敢于面对高阶计算，并完成这一纲领。在他那两篇极富洞察力的高水准论文里，戴森指出这种极端困难的分析主要的症结所在，并且解决了问题。重整化这种纲领，把可加的减法转化成可乘的重整化，其有效性还需要一个绝非平凡的证明，而这个证明是戴森提出的。他定义了本原发散性（primitive divergence）、骨架图（skeleton graph）以及重叠发散（overlapping divergence）等概念。利用这些概念，他深刻分析问题，完成了量子电动力学可以重整化的证明。他的洞察力和能力是惊人的。

错身而过的荣耀

杨振宁提到的两篇论文就是 “朝永、史温格和费曼的辐射理论” 及其续篇 “量子电动力学的 S 矩阵”（The S matrix in quantum electrodynamics）。杨振宁曾在给笔者的邮件中特别指出，这两篇论文各有其重要性：前者证明了费曼图的正确性，而在此之前费曼仅只提出了构想；后者则解决了高阶计算的难题，登上朝永、史温格和费曼此前从未达到的高度。后来一般咸认：与朝永、史温格和费曼一样，戴森也是量子电动力学的奠基人。这尤其体现在史韦伯（Silvan Schweber）1994 年出版的《QED 及其缔造者：戴森、费曼、史温格和朝永振一郎》（QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga）一书中，该书第九章专门介绍了戴森的贡献。

对戴森未能获得诺贝尔奖，深表惋惜的还有 1979 年诺贝尔物理学奖得主温伯格（Steven Weinberg），温伯格认为 “诺贝尔委员会‘耍了（fleeced）’他”。但戴森对与诺贝尔奖无缘并不遗憾。他说：“无庸置疑的是：为了获得诺贝尔奖，你必须有持久的注意力，要抓住某些深刻而重要的问题，至少坚持十年。但这不是我的风格。”(维基百科) 这句大实话切中肯綮，不由让人联想起杨振宁论述科学家的风格与贡献之关系的一段著名论断（[7]）：

在创造性活动的每个领域里，一个人的品味，加上他的能力、气质和际遇，决定了他的风格，而这种品味和风格又进一步决定了他的贡献。品味和风格竟然与他对物理学的贡献如此关系密切，乍听之下也许会令人感到惊讶，因为物理学通常被认为是一门客观地研究物质世界的学问。然而，物质世界有其结构，而一个人对这些结构的洞察力，对这些结构某些特点的喜爱、某些特点的憎恶，正是他形成自己风格的要素。因此，品味和风格之于科学研究，就像它们对文学、绘画和音乐一样至关重要，这其实并不是稀奇的事情。

以上这段话深得戴森欣赏，他在纽约州立大学石溪分校为杨振宁荣誉退休举办的晚宴讲演 “杨振宁 —— 保守的革命者”（Chen Ning Yang, A Conservative Revolutionary, 见 [8]），也引用了这段话。戴森很清楚，他本人就是 “品味和风格决定贡献” 的一个明证。

再度借用杨振宁常说的语汇 —— 我们可以说，戴森在这一年完成了他作为年轻人的 “猛冲（push）”。重要的结果是，普林斯顿高等研究院院长奥本海默授予他长期研究职位，这对年仅 25 岁的年轻人来说是极为难得的。此后，奥本海默持续器重戴森，甚至期望他成为新的波耳（Niels Bohr）或爱因斯坦。然而，这不是戴森的风格。戴森在《宇宙波澜》中曾如此评价这位如父亲般待他的长者：

奥本海默对物理学怀抱真正终生不倦的热情。他总持续不断努力，去认识自然界的基本祕密。我因为没能成为深刻的思想家而令他失望。当他一时冲动指定我担任研究院的长期职位时，他期望得到的是年轻的波耳或爱因斯坦。如果那时他征求我的意见，我会告诉他，迪克（Dick, 费曼的昵称）才是你要的人，我不是【注：根据费曼在《别逗了，费曼先生》（Surely You’re Joking, Mr. Feynman! ）中的自述，高等研究院元老确实对费曼有如此期许，也给费曼发过聘函，但被费曼拒绝了】。一直以来，我都是个问题解决者，而不是思想创造者。我不能像波耳和费曼那样，持续经年，将全部心血都倾注在同一个深奥的问题上。我感兴趣的不同事情太多了。

康奈尔与普林斯顿

1949 年，戴森回到英国，在伯明罕大学担任研究员。物理系主任派尔斯（Rudolf Peierls）热忱欢迎他的到来，刚取得博士学位的萨拉姆（Abdus Salam）打电话给他的 “偶像” 戴森，请求拜访。这次会面激发萨拉姆推进了戴森关于重整化的工作，开启他个人辉煌的学术生涯。

1950 年，戴森与当时在普林斯顿高等研究院访问的数学家胡贝尔（Verena Huber）结婚。

1951 年，戴森返美。为了争取人才，康奈尔大学破格聘任没有博士学位的戴森为物理教授【注：戴森本人并无博士学位，贝特虽然指导戴森，但他们不是正式的导师研究生关系。戴森之成才，主要是靠自学】。一直到 1953 年，戴森在康奈尔一边授课，一边指导麾下的博士后和研究生做理论计算【注：在康奈尔，戴森还与年轻的华裔数学家钟开莱有过学术交往，解决了钟开莱向他提出的一个数学问题】。他的讲义《高等量子力学》（Advanced Quantum Mechanics）帮助许多学子进入这个领域，60 多年后正式出版成书。

1940 年代的费米（维基）

而在指导学生方面，戴森自认是极其失败的，此后不再带研究生。故事是这样的：当戴森与学生获得某些进展后，他前往芝加哥大学拜访该领域的专家费米。戴森自豪地呈交计算结果，期待费米的认可与激动反应。出乎意料的是，费米竟然丝毫不为所动，只是平静指出，“计算方法有两种：第一种是我所钟爱的，基于清晰的物理图像；第二种是基于严格的数学构架。你的计算，两个条件无一符合。” 对于费米的批评，戴森心悦诚服。事实上他们的计算结果与实验资料也并非特别吻合。1999 年，在费米的学生、同时也是戴森的老同事杨振宁的荣休晚宴上，戴森心存感激地回忆起费米为他上的这堂关键课程（见 [8]）：

…… 虽然我不是费米的学生，但我有幸在学术生涯的关键时刻与费米相谈 20 分钟。我从这 20 分钟里所学到的，比我从奥本海默 20 年里学到的还要多。…… 在这 20 分钟里，他脚踏实地的见识，省掉了我们好几年的无谓计算。

回到康奈尔，戴森意识到学生这两年的功夫白费了，这让他极为愧疚，并造成极大的阴影。为了避免再度误人子弟，他决定不再带研究生。将戴森从沮丧与内疚中拯救出来的，是奥本海默的聘约。1953 年，戴森告别康奈尔，来到普林斯顿，而立之年的戴森被聘为高等研究院的教授，直到 1994 年退休。应该说，戴森在这里如鱼得水，找到了家。

高等研究院院徽。左边是 Truth，右边是 Beauty。整个设计受到济慈名诗《希腊古瓮颂》（Ode on a Grecian Urn）的启发：美者真，真者美─此即尔等在人世所共知，所应共知。（余光中译）

《规范理论与对称之美 —— 杨振宁传》（天下文化）的作者、台湾《中国时报》前科学主笔江才健曾在对戴森的访谈中，问起他对高等研究院的看法 (见 [9])：

江才健问：我记得杨振宁由芝加哥大学来这里（普林斯顿高等研究院）工作以前，他的老师费米告诉他，说这里像修道院，可以待一阵子但不能久留。杨振宁在此待了 17 年，而您却待了 40 年，对于费米的话，您有什么看法？

戴森答：这因人而异。我想杨振宁离去是对的，因为他需要更大的天地，成就更大的事业。对我来说，留在这里很好，因为我不是一个帝国建造者，我在此很开心，花时间于做研究与写书，我很满意。虽然年岁日老，但可以一直维持我的活力。

能够在普林斯顿高等研究院这个修道院里工作，当属戴森一生中最大的幸运。戴森在高等研究院结交了许多科学同仁。例如，在研究院的同事与访问学者中就有杨振宁、李政道、梅塔（Madan Lal Mehta）、约斯特（Res Jost）、勒纳（Andrew Lenard）。与戴森交流频繁的还有附近普林斯顿大学的教授威格纳（Eugene Wigner）、巴格曼（Valentine Bargmann）、利柏（Elliott Lieb）等。戴森的许多工作，就是藉由与他们的交流讨论而成型的。

利柏（2011）（维基）

1957 年，出于细故 —— 英国政府不承认戴森在瑞士和美国生的孩子，拒绝核发护照 —— 导致戴森最终加入美国籍。戴森在收于《从爱神到盖娅》的 “引路人” 一文中写道：「我原是英国人，只是阴错阳差才加入美国籍。我同时为这两个国家而骄傲。」笔者曾向戴森请教英美两国间的文化差异。他答复说：

英、美两国的文化在许多方面都不同。英国历史更悠久、文化更灿烂，但对生活持悲观态度。而美国有更多样化的公民，科技强盛，并为年轻人提供了许多机会。最明显的一个差别体现在对待游戏和竞技体育的态度上。英国的孩子受到的教育是：最重要的事情是成为大度的失败者，竞争必须确保公平，纵使失败也必须不失风度。而美国的孩子接受的教育是，成为胜利者才是最重要的，要想方设法赢得胜利。这两种文化都很珍贵。我很高兴这个世界同时保有它们存在的空间。

---

戴森传奇 —— 从数论、QED 到科普写作大师（下）

原创 林开亮 数理人文 2016 年 12 月 16 日 00:13

作者简介：林开亮，首都师范大学数学博士，目前任教于西北农林科技大学理学院。

戴森，摄于 2005 年（维基）

我人生中最重要的三件事，依序是：家庭、朋友和工作。所以我最大的贡献是养育六个儿女，他们都在不同领域事业有成，也都已成家。我自己的工作则没那么重要，而且我身为作家的工作成就，或许还比我作为科学家的成就重要。—— 戴森，2012 年 11 月 21 日致笔者函

后续的物理与数学工作

美国数学学会（AMS）1996 年出版的《戴森论文选集及评注》（Selected Papers of Freeman Dyson with Commentary），收录了戴森至 1990 年为止最重要的科学成果。该书模仿杨振宁 1983 年出版的《杨振宁论文选集及评注》（Selected Papers of Chen Ning Yang with Commentary）的格式，将 49 页的评注集结在一起，置于全书开端，构成他的科学自传。正如杨振宁的评注描述了杨振宁之所以成为杨振宁，戴森的评注也描述了戴森之所以成为戴森。

《戴森论文选集及评注》收入的研究成果分为三个领域─数学、物理、工程学与生物学。本文只介绍他的物理和数学工作。

在戴森 1948 年后的所有物理研究中，特别值得一提的有两笔。其一是 1961 年关于随机矩阵的工作，这是戴森与其创立者威格纳交谈的结果。对戴森而言，这个成果令他极为兴奋，他在选集评注中写道：

1961 年我在布鲁克海文度学术假，以极快的速度写完了三篇系列论文。彷彿我每天都发现全新待解答的问题，每一个优美的等式，第二天又引出另一个更加优美的等式。

其后若干年，戴森仍不时回到这一主题。由于威格纳、梅塔、高登（Michel Gaudin）、戴森等人的努力，随机矩阵发展成一门系统性学问，直到今日依旧热门。戴森与造访高等研究院的数论专家蒙哥马利（Hugh Montgomery）是在偶然交谈下，促成两人发现了随机矩阵与数论中的黎曼假设之间的微妙关联，此事常被传为美谈。

戴森的另一项重要成果属于统计物理。1965-1966 年他与勒纳合作，首次从数学上严格证明了物质的稳定性。这是一年前由费雪（Michael Fisher）和卢埃勒（David Ruelle）提出悬赏的问题（奖品是香槟一瓶）。戴森与勒纳应用的数学技巧，源于他 1957 年的一篇论文，该篇论文曾改进了杨振宁和李政道的工作。戴森与勒纳将近 40 页的复杂证明，在 10 年后被利柏和提林（Walter Thirring）简化到不足三页。对此，戴森在《戴森论文选集及评注》中反省到：

为什么我们的证明如此糟糕，而他们（利柏和提林）的证明如此优美？原因很简单。我和勒纳的证明是从一些数学技巧出发，在不等式的丛林中披荆斩棘，没有任何来自物理方面的想法作指引。而利柏和提林是从物理思想 —— 物质之所以稳定，是因为经典的汤玛斯费米原子模型（Thomas-Fermi model）是稳定的 —— 出发，寻求合适的数学语言将这个想法转化为严格的证明。我在剑桥求学时，数学家李托伍德曾在课堂上讲，第一流的数学家是那些发表糟糕证明的数学家。一流的数学家发表糟糕的证明之后，二流数学家研究细节并给出更好的证明。物质稳定性的两个证明，为李托伍德的格言提供了反例。利柏和提林找到了好的证明，他们既是一流的数学家，也是一流的物理学家。我们的糟糕证明主要价值在于，它激励了利柏和提林去寻求更优美的证明。

2007 年，戴森摄于普林斯顿高等研究院（维基）

数学界的影响力

虽然身在主流数学之外，戴森在数学界也颇有影响力。整体而言，数学家更欣赏他的数学观，因此戴森常受邀到各种场合演讲。例如，1965 年他应美国工业与应用数学会（SIAM）邀请，以 “群论在粒子物理中的应用” 为题出席冯・诺伊曼讲座（John von Neumann Lecture）。1972 年，他应美国数学学会之邀，做了题为 “错失的机会”（Missed opportunities）的吉布斯讲座（Josiah Willard Gibbs Lecture）。

在吉布斯演讲中，戴森列举许多案例，有力地表明，数学家由于与物理学家的疏远，错失了许多重要发现的机会（例如麦克斯韦方程中所隐含的狭义相对论原理）。戴森以他本人的教训现身说法，呼吁数学家多与物理学家对话，一起推动科学研究 —— 他错失了独立于数学家麦克唐纳（Ian Macdonald）发现模形式与仿射李代数之间的奇妙联系的机会，“而这仅仅是因为数论学家戴森和物理学家戴森没有彼此沟通。”

$$\tau (n)=\sum \frac{(a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e)}{1!2!3!4!}$$

戴森心中最美的方程 —— Macdonald 等式，其中左边的 $\tau (n)$ 是拉马努金的 $\tau$ 函数，而右边的求和取遍所有满足下述三个条件的五元整数组 $(a,b,c,d,e)$：

1. $a,b,c,d,e\equiv 1,2,3,4,5(\mathrm{mod}5)$
2. $a+b+c+d+e=0$
3. $a^2+b^2+c^2+d^2+e^2=10n$

戴森的演讲才能也许受到了马丁・路德・金（Martin Luther King）的激发。他在《宇宙波澜》书中曾提起金恩在 1963 年 8 月 28 日的著名演讲 “I have a dream”：

金讲得像《旧约全书》里的预言家。我离他极近，听他演讲时我流泪了，流泪的也不止我一个。“I have a dream.” 他在向我们描述他对和平与正义的展望时，一遍又一遍地重复着这句话。我在那天夜里的家书中写道：“我随时准备为他蹲监狱。” 当时我并不知道自己听到的是人类历史上最著名的演讲，只知道这是我听过的最伟大的演讲。我更没想到，金会在五年之后遇刺身亡。

拉马努金（维基）

1987 年，伟大的印度传奇数学家拉马努金百年诞辰，戴森因为早年对拉马努金的工作有过研究而受邀参加学术纪念活动。他以 “拉马努金花园漫步” 为题演讲。在演讲中，他希望数学家与物理学家关注拉马努金生前的最后一项卓越发现 —— 仿 theta 函数（mock theta functions）。他充满寄託的说道（令人联想起马丁・路德・金）：

我的梦想是，在我有生之年能看到，我们年轻的物理学家实现超弦理论所预言的内容与大自然的事实之间的对应，从 theta 函数扩展到仿 theta 函数。

15 年后的 200 年，荷兰的青年数学家茨威格斯（Sander Zwegers）在德国普朗克数学研究所的数学家札基尔（Don Zagier）的指导下，完成了题为 “仿 theta 函数” 的博士学位论文。在此基础上，2008 年，美国威斯康辛大学的数学家布瑞曼（Kathrin Bringmann）与小野健（Ken Ono）又向前推进一步。与戴森的预言更契合的，是出生于台湾的数学物理学家程之宁（Miranda Chih-Ning Cheng）及其合作者在 2012 年提出、并由小野等人在 2015 年证明的 “伴影月光猜想（Umbral Moonshine Conjecture）”。这一点连程之宁教授本人也是同意的，她在邮件中答复我说，她当初提出这个猜想时并没有想到戴森的话。他们的工作一起回应戴森的呼吁，实现了他的部分梦想。戴森的数学远见由此可见一斑。

鸟与蛙

2008 年，戴森为美国数学学会的爱因斯坦讲座准备了以 “鸟与蛙”（Birds and Frogs）为题的演讲。讲座因戴森生病而临时取消，但讲稿则公开发表。该演讲的基本观点取自《全方位的无限》，但立意更高，提及许多有趣味富哲理的话题。戴森在开篇写道：

有些数学家是飞鸟，其他的是蛙。鸟儿高翔天际，遍览直至天际的广阔数学远景，他们所喜爱的，是能统摄我们的思想、将散布于地上各处的种种问题整合起来的概念。青蛙住在泥地里，只能看到长在附近的花朵。他们喜爱特定事物的细节，一次只解决一个问题。我刚好是一隻蛙，但是我的许多好友都是飞鸟。我今晚演讲的主题是这样的：数学需要鸟，也需要蛙。数学既丰富而且优美；因为有飞鸟赋予它宽阔的远景，有蛙儿赋予它精致的细节。数学既是伟大的艺术，也是重要的科学；因为它结合了概念的普遍性和结构的深刻性。倘若有人宣称鸟儿因为看得更辽远而胜过蛙，或是青蛙因为观察更深刻而胜过鸟，两种说法都是愚蠢的。数学的世界既广阔又深刻，我们需要鸟与蛙齐心协力才能探索。

鸟与蛙这个比喻如此之妙，不由得令人怀疑，戴森是不是引申了古希腊诗人阿基罗库斯（Archilochus）关于刺蝟和狐狸的比喻，如同作家伯林（Isaiah Berlin）曾藉此评论托尔斯泰（Leo Tolstoy）的历史观一样。笔者曾透过邮件询问戴森，“鸟与蛙” 这个标题，是否受到阿基罗库斯关于哲学家分为 “狐狸与刺猬” 两类的启发？他答复说：“是，演讲的标题来自希腊戏剧家阿里斯多芬（Aristophanes），他曾写过两部著名的戏剧《鸟》与《蛙》，但其思想则又近似阿基罗库斯的狐狸 / 刺猬的二分法。我发现，对两种数学家来说，青蛙与飞鸟是更好的比喻。”

戴森在文中举出了青蛙与飞鸟的诸多例子，如培根与笛卡儿、贝西柯维契与魏尔（Hermann Weyl）、冯・诺伊曼与马宁（Yurin Manin），并含蓄地将他本人与杨振宁作为另一对比较的例子：

在我受业于贝西科维契之后过了几年，我来到普林斯顿，并结识了魏尔。…… 他对我印象很好，因为那一年我在美国的《数学年刊》（Annals of Mathematics）发表了数论的论文，在《物理评论》（Physical Review）发表了量子辐射理论的论文。魏尔是当时世上少数几个能够同时悠游于这两个领域的人之一。他欢迎我来到研究院，期望我能和他一样成为飞鸟。我令他失望了，我仍固执地当一只蛙。…… 在魏尔离开普林斯顿后不久，杨振宁从芝加哥过来，搬进魏尔的旧宅。杨振宁接替魏尔的位子，成为我们这一代物理学家领头的飞鸟。在魏尔仍在世时，杨振宁和他的学生米尔斯（Robert Mills）发现了非交换规范场的杨 - 米尔斯理论【注：魏尔 1955 年去世，杨 - 米尔斯论文 1954 年发表】，这是魏尔的规范场极其优雅的推广。

魏尔（左）、奥本海默（右）（维基）

第一段话与前述戴森追忆奥本海默的话何其神似！真是难以想像，年仅 25 岁的戴森能同时被数学界的领袖魏尔和物理学界的首脑奥本海默如此垂青。要知道，身为魏尔物理学传人的杨振宁，毕生最大的遗憾之一，就是不知道曾经近在咫尺的魏尔，原来一直对规范原理念念不忘。杨振宁曾写道（见 [10]）：

在物理学家中，没有人知道他（魏尔）对规范场思想的兴趣如此锲而不舍。无论是奥本海默还是包立，都从未提及这点。猜测他们也没有把我和米尔斯 1954 年发表的论文告诉他。如果他们告诉他，或者他偶然发现了我们的文章，那么可想而知，他一定会非常高兴、非常激动。因为我们把他最珍爱的两样东西 —— 规范场和李群 —— 放在一起了。

杨振宁的遗憾真可以用 “世界上最遥远的距离不是生离死别，而是我站在你面前，你却不知道我爱你” 来形容。这里的 “你” 就是飞鸟魏尔。鸟与蛙的比喻凸显了杨振宁与戴森的差别，正如杨振宁曾借用狐狸与刺猬的比喻来彰显中国近代两位著名数学家华罗庚与陈省身的不同。

戴森在这篇讲稿中，还以开玩笑方式建议了解决黎曼假说的可能途径（转而考虑准晶体的枚举与分类）。可以看出，戴森一直没有放下他年少时的梦想（证明黎曼假说），就像屈原所说的 “余幼好此奇服兮，年既老而不衰”。

由于戴森对冯・诺伊曼的工作（如博弈论与电脑理论）至感兴趣，2010 年 5 月，他应邀在布朗大学提出 “漫步在冯・诺伊曼的花园” 的通俗演讲。从两次演讲的标题 “漫步在冯・诺伊曼的花园” 和 “漫步在拉马努金的花园” 可以看出，戴森倾向于将数学视为智力上的消遣。也许，数学在他眼里，与其说是智力的拼搏，毋宁说是探险猎奇。

戴森仍然不时回到纯数学研究中。2012 年，将近 90 高龄的戴森还在数学刊物《拉马努金期刊》（The Ramanujan Journal）上发表题为 “分拆与巨正则系综”（Partitions and the grand canonical ensemble）的论文， 还与普雷斯（William Press）合作在《美国国家科学院院刊》（PNAS）上发表了一篇关于博弈论中 “囚徒困境” 的研究论文 “迭代囚犯困境具备宰制任何演化对手的策略”（Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent）。

不过戴森认为，他自 1990 年以后的那些数学与物理研究，较侧重其趣味性，谈不上特别的学术性。他在为《科学的面孔》写的自传中说道（见 [2]）：

大多数科学家把科学当成类似盖房子或烹饪的技能，少数科学家把科学当作哲学探索。我属于前者。我从不关心我要解决的问题是否重要。纯数学领域无关紧要的问题，与原子物理学和生物学的重要问题同样有趣。

2015 年 5 月，新加坡世界科学出版社出版了戴森的一本新书，收集了他自选 1990-2014 年间的代表性文章，书名就叫《鸟与蛙》（Birds and Frogs: Selected Papers, 1990-2014）。此书可看作他 1996 年《论文选集及评注》的续篇，但其侧重点跟《从爱神到盖娅》一样，收入的大多是通俗文章而非专业论文。

科学人文写作

1975 年，美国史隆基金会（Alfred P. Sloan Foundation）邀请戴森写一本科学自传。在考虑如何回复时，戴森想起了老师哈代的话「年轻人应该证明定理，而老年人应该写书。」于是接受邀约，开启了他的写作生涯。这引出了他的处女作《宇宙波澜》（1979）。戴森曾说，他的生命是从 55 岁开始的，因为在那年，他完成了第一部作品。自此以后，戴森花费在研究和写作的时间各占一半。戴森作为作家的名声，很快超越了他作为科学家的名望，其作品列表可见附录。因其杰出成就，1996 年戴森获得了享有 “诗人科学家” 美誉的汤玛斯奖（Lewis Thomas Prize）。

《宇宙波澜》可谓戴森最重要的科普著作。该书曾被译成七种语言。书名 Disturbing the Universe 取自诗人艾略特（T.S. Eliot）的名作 “普鲁弗洛克的情歌”（The Love Song of J. Alfred Prufrock）。据戴森给笔者的回信，书名的含义是 —— 我们未来的活动将改变宇宙的命运。1993 年，戴森为邱显正译的《宇宙波澜》写过一篇精彩的序言，其中他写道：

本书从浪漫的角度来看科学世界，把科学家的生活比作个人灵魂的航程；它有意略过每个科学家生活、工作所在的机构，以及政治、经济的既定框架。在科学史上，团体与个人是等量齐观的，但大多数历史学家往往侧重于机构与团体的活动。本书特别强调个人，因为我希望写点新鲜而与众不同的东西。我对科学的浪漫观点虽然并不代表全部的真理，却是真理中不可或缺的重点。…… 本书于 14 年前在美国付梓，之后我又陆续为非专业的读者写了四本书，然而《宇宙波澜》仍然是我的最爱。它是我的第一本书，字字发自肺腑，比其他几本书投注了更多的心血和情感。如果我的著作只有一本能流传千古，而我又有权选择哪一本的话，我将毫不犹豫选择这一本。

《宇宙波澜》 想必能够流传千古。因为戴森兴趣广泛，人生阅历丰富，本书读起来颇有趣味。书中第六章专门回忆了他与费曼 1948 年为期四天的阿布奎基驾车之旅，途中与费曼的反复讨论，使戴森终于对费曼的路径积分法（也称 “对历史求和”）有了深刻的领悟。戴森与费曼的结伴同行，起初只是一个偶然的局部事件，但对戴森和费曼两人的一生都产生了深远的影响，最后并深刻改变了 20 世纪物理学的整体面貌。戴森认为这是他一生最幸运的际遇。

这些年来，戴森一直笔耕不辍。除了著书以外，他还写了许多有趣的文章。例如 1955 年，普林斯顿高等研究院的永久成员魏尔逝世，戴森为英国顶级科学刊物《自然》（Nature）撰写一篇简短的追悼文，转述了魏尔身为当世纪大数学家的价值观：

他 [魏尔] 曾半开玩笑地对我说：“我的研究永远试图将真与美结合；但若两者只能择其一，我选择的通常是美。”

1988 年费曼过世时，戴森根据他过去写给双亲的家书，编辑成一篇回忆文章 “费曼在 1948”（Feymann in 1948，收于《从爱神到盖娅》）。事实上，近年来出生于 20 世纪初的大物理学家相继去世，而新世纪的到来又适逢许多大物理学家的百年诞辰。许多与戴森有过交往的学者，例如泡利、费米、狄拉克、奥本海默、贝特、泰勒（Edward Teller）、钱卓拉赛卡（S. Chandrasekhar）、坎梅尔、惠勒（J. A. Wheeler）、萨拉姆等，他都写了忆旧文。

戴森还不时为《纽约客》（New Yorker）与《科学美国人》（Scientific American）撰稿，也常常为新出版的各类科学著作写序文和书评，因此他的名字频繁出现在《纽约书评》（New York Review of Books）杂志上。2013 年，浙江大学出版社出版了戴森书评集 The Scientist as Rebel 的中译本《反叛的科学家》。2015 年，戴森出版第二本书评集《天地之梦》（Dreams of Earth and Sky），即将由浙江大学出版社出版。近年来台湾或大陆出版的许多优秀的科普书，其中许多戴森都写过书评。

游走数学和物理的边缘

作为数学家，戴森的数学能力毋庸置疑。但他并不以数学家的身份为傲。在他看来，有些数学家过于离群索居、缺乏人情味。他日后之所以与妻子赫伯离婚，正是因为她是个数学疯子，沉湎于数学不能自拔，甚至置子女于不顾，而且从来未被点醒过 —— 不像戴森年少时曾被母亲点醒。1958 年，戴森与马拉松长跑运动员容格（Imme Jung）再婚。戴森共有六个孩子，其中五个是女儿，唯一的儿子乔治（George Dyson）是著名的科学史家。

哈代（维基）

戴森的数学生涯与剑桥数学学派，尤其是哈代有密切关联。正是哈代与莱特合著的《数论导引》，引发了戴森对数论长达一生的兴趣。应该指出，虽然戴森学习和吸收新知的能力很强，但他在两年大学期间，学到的数学其实很有限。正如戴森在给笔者的信中说起的，他的老师哈代和李托伍德身为英国的数学领袖，甚至阻碍了英国数学的进展：

哈代和李托伍德是旧式的数学家，他们虽然活在 20 世纪，做的却是 19 世纪的数学。他们虽然做出了漂亮的工作，但他们对源于法国和德国的新抽象思想没有兴趣。以致于年轻一代的英国数学家，包括我，成长的环境皆距离繁荣于法国的新数学十分遥远。

事实上，数学 1930-40 年代经历了迅猛的发展，然而哈代和李托伍德忙于研究古典数学（解析数论与古典分析），导致英国下一代数学家没有及时跟上抽象代数与拓扑学兴起的现代数学潮流。在当时的剑桥，只有霍奇是唯一的例外。他不仅跟上现代数学的步伐，而且就在戴森入学剑桥前后，做出丰硕的成果，然而戴森并不受霍奇的讲课所吸引。凡此种种，皆导致戴森对数学缺乏较为全面的了解。戴森的数学视野和品味也就局限于哈代、李托伍德与拉马努金的范围之内。而这些人的工作（解析数论与离散数学）都偏离后来主流数学太远了。戴森虽然早期在数论研究中做出了一些有价值的成果，但他对纯数学中曲高和寡的冷清氛围不满意，于是决定离开纯数学而转向应用数学。他在《太阳、基因组与互联网》的导言中写道：

在日后的科学生涯中，我并未忠于哈代的理想。起初我步他的后尘进入数论领域，并解决了几个数论问题。这些问题虽然优美，但无关宏旨。后来，在作为数论专家工作了三年之后，我决定做应用数学家。我认为，比起继续证明只能引起一小撮数学家感兴趣的定理，理解自然的基本奥祕要令人激动得多。

作为物理学家，在很早的时候，由于费米的提点，戴森意识到物理研究不能仅仅靠纯粹的数学演算，更需要物理直觉的指引。戴森很清楚，他缺乏物理直觉。他在物理学上的成功得益于与物理学家的广泛交流，得益于他的数学品味和才能─他以数学家的价值观来做物理。

他在 1964 年发表于《科学美国人》的文章《物理科学中的数学（Mathematics in Physical Sciences）》中写道：“数学之于物理，不仅是计算现象的工具，更是创造新理论的概念和原理的主要源泉。” 有如共鸣，杨振宁也曾表达过类似的见解（见 [7]）：“我的大多数物理学同事对数学采取一种功利主义的态度，而也许是因为受父亲的影响，我较为欣赏数学。我欣赏数学家的价值观，崇拜数学的优美和力量：它有战术上的巧妙灵活，又有战略上的雄才远虑。而且，奇迹的奇迹，它的一些美妙概念，竟是支配物理世界的基本结构！”

但是，物理学家与数学家有不同的价值观，戴森的价值观并没有得到物理学家的广泛认同。这与数学家对他的看法恰好形成鲜明对比。数学家不认为戴森的数学工作很重要，但愿意听他的数学见解【注：例如当代著名数学家阿提雅（M. Atiyah）在他的第五卷《论文选集》序言中，就提到了曾受益于与戴森的交谈】；而物理学家虽认可戴森的物理成就（例如他荣获 1981 年沃尔夫物理奖），但拒绝他的数学价值观。

戴森在《不合时尚的追求（Unfashionable pursuits）》一文中，将自己定位为 “数学物理学家”。他将数学物理这门学科的宗旨理解为─用纯数学的严格风格和方法来理解物理现象。数学物理学家的目标是，澄清那些作为物理理论奠基石之概念的精确数学意义。戴森是名符其实的数学物理学家，并且得到了高度认可。在 2012 年的国际数学物理大会（ICMP）上，戴森获得了该领域的最高奖 —— 国际数学物理协会颁发的庞加莱奖（Henri Poincaré Prize）。

然而，不论是作为数学家还是物理学家，戴森都只获得部分的成功。唯有作为作家的戴森，才算是取得全面的成功。如果要从 20 世纪的数学家中挑选出 100 位最有成就的数学家，戴森应该是无法入围。因此，他年少时期望名列 20 世纪《数学精英》系列人物之一的梦想势必落空。而作为物理学家，虽然他早在 25 岁就名扬四海，但他也从来没有自我期许成为像他的同事杨振宁那样的伟大人物。

结语：以作家名世

一直以来，物理学界似乎都对戴森有更高的期许，例如普林斯顿大学物理教授、1977 年诺贝尔物理学奖得主安德森（Philip Anderson），在针对谢尔维（P. F. Schewe）的戴森传记撰写的书评 “一个多面手的生涯”（An iconoclast’s career）中写道：“戴森是个能力超强的人，并且成就巨大，然而，如果他术业有专攻，又会是怎样呢？” 这大概是在期待戴森成为 “刺猬” 或 “飞鸟”。但应该指出的是，戴森的广泛兴趣与大胆假设，使他看起来像个擅长综合的人，人们也期待他成为能够总揽全域的人，但其实他的第一身份是数学家，更擅长的是分析和小心求证。

也许戴森在 20 世纪的数学界和物理学界无法佔有特别高的地位，但作为科学家中的作家，他绝对是首屈一指的。

戴森曾回复笔者，在写作上对他影响最大的是哈代，因为他为非数学专业的读者写出了优秀的书籍《一个数学家的辩白》。哈代的写作确实吸引人，这也许肇因于他曾经历过数学史上最浪漫的传奇，发现了自学成才的印度数学拉马努金，所以写作也富有激情。不过，哈代的言论较为极端，一旦绝对化，就会创造出奇异的美感和坚不可摧的力量，往往令读者不自觉地信以为真。例如哈代在《一个数学家的辩白》中曾写道：

只有少部分数学有用，而即此少部分也较为乏味。“纯正” 数学家的 “纯正” 数学（无论其为 “应用” 数学或 “纯粹” 数学），即费马、欧拉、高斯、阿贝尔、黎曼的数学，几乎全部无用。如能解释真正数学的存在，则应解释为艺术。

这方面，哈代有点像英国文学家王尔德（Oscar Wilde），另一个 “语不惊人死不休” 的天才。又因为哈代先后经历了两次世界大战，而他慧眼识出的天才拉马努金又英年早逝，所以他暮年提笔时，处处洋溢著悲观情绪，这也许在无形中打动了某些读者。但哈代的有些话是经不起检验的，比如他说 “费马、欧拉、高斯、阿贝尔、黎曼的数学几乎全部无用” 就错得离谱。

对于写作和数学研究，哈代完全以美为至高法则。他在《一个数学家的辩白》中写道：

美是首要的试金石：丑陋的数学不可见于天日。

可以说，哈代是个 “纯” 到了极致的数学家，比魏尔还要纯。笔者曾在通信中询问戴森：真与美二选一，他会选择哪一个？他回复说，不同于哈代和魏尔，他只有在做研究时会优先考虑真实，而在讲故事时则会优先考虑美妙。

相对而言，戴森的文字则不时闪现着睿智与幽默，其评判也较中和。对于看似矛盾的说法，他可以藉由波耳的互补原理和海森堡的测不准原理为哲学基础来调和。而且，戴森的视野比哈代开阔。他早年读到的凡尔纳、托尔斯泰、威尔斯（H.G. Wells）、霍尔丹、赫胥黎（Aldous Huxley）、奥威尔（George Orwell）的作品对他有钜大影响。像那些前辈一样，戴森具有非凡的想像力与洞察力。此外，戴森在写作中常旁徵博引，尤其是戏剧和诗歌─这是自小受父母薰陶和中学时代受弗兰克影响的结果，为其作品增色不少。例如在《宇宙波澜》一书的索引中，你可以看到许多诗人和作家的名字，如奥登（W.H. Auden）、布雷克（William Blake）、歌德、弥尔顿、莎士比亚和叶慈（W.B. Yeats）。戴森在《生命起源》中说，他最喜欢的诗人是布雷克，因为即便他所作的猜想或预言最终被证明是错误的，布雷克的名句已足以让他释然：To be an Error and to be Cast out is a part of God’s design（铸成错误并被摈弃，亦属上苍精心设计）。哈代与戴森的共同点，也许可以用培根的名言来概括：“绝美之中必有奇异之处。” 而如果要指明戴森与哈代的差别，也许我们可以窃取哈代本人在《一个数学家的辩白》中的话：

假如真能把我的雕像塑在伦敦广场的纪念碑上，我会希望这座碑高耸入云，以至于人们见不到雕像呢？还是希望纪念碑矮得足以使人们对雕像一目了然呢？我会选择前者。可以想见，戴森 [原文史诺博士] 会选择后者。

笔者曾询问戴森是否同意后面这个说法？他表示同意。事实上，戴森在《从爱神到盖娅》的序文中说：“我所有的作品，其目的都是打开一扇窗，让高居科学庙堂之内的专家望一望外面的世界，让身处学术象牙塔之外的普通大众瞄一瞄里面的天地。” 他成功了。

戴森的著作不仅带给读者亲切感，更令人感受到科学家的强烈使命感。也许我们可以借用司马迁在《史记》中评价屈原的一句话，来评价作为作家的戴森：“其志洁，故其称物芳。”

---

一、延伸阅读

1. 戴森科普著作与相关译文
   戴森所有科普著作可参考下文“戴森科普性书籍列表”，亦推荐阅读《数理人文》杂志的两篇译文：

   • 赵学信译. 鸟与蛙[J]. 数理人文, 2014(2).
     在线链接：http://yaucenter.nctu.edu.tw/journal/201406/ch9/main.php

   • 赵学信译. 漫步在冯诺曼的花园[J]. 数理人文, 2015(3).
     在线链接：http://yaucenter.nctu.edu.tw/journal/201501/ch4/main.php

2. 戴森90大寿暨任职60周年庆祝会相关

   • 主题：Dreams of Earth and Sky（《地与天之梦》）
   • 背景：2013 年普林斯顿高等研究院（IAS）为戴森举办 90 大寿暨任职 60 周年庆祝会
   • 官方网页链接：https://www.ias.edu/ideas/2013/dreams-of-earth-and-sky-celebratio

3. 戴森相关传记与学术著作

   • P.F. Schewe. Maverick Genius: The Pioneering Odyssey of Freeman Dyson[M]. New York: Thomas Dunne Books/St. Martin’s Press, 2013.
   • S. Schweber. QED and the Men who Made it: Dyson, Feynman, Schwinger, and Tomonaga[M]. Princeton: Princeton University Press, 1994.

二、戴森科普性书籍列表（含中译本）

出版年份	英文书名（原文信息）	中译本信息
1979	Disturbing the Universe 出版社：Basic Books	1. 陈式苏等译. 宇宙波澜[M]. 上海：上海科学技术文献出版社, 1982. 2. 邱显正译. 宇宙波澜：科技与人类前途的自省[M]. 台北：天下文化, 1993；北京：三联书店, 1998.
1984	Weapons and Hope（《武器与希望》） 出版社：Harper & Row	无中译本信息
1986	Origins of Life（《生命的起源》） 出版社：Cambridge University Press（1999年第2版）	无中译本信息（注：本文后续提及将收入“即将出版的戴森中译著作《生命起源》”）
1988	Infinite in All Directions 出版社：Harper & Row	李笃中译. 全方位的无限[M]. 台北：天下文化（1991年两册本、1996年合订本）；北京：三联书店, 2004.
1992	From Eros to Gaia（《从爱神到盖娅》） 出版社：Pantheon Books	无中译本信息
1997	Imagined World 出版社：Harvard University Press	1. 杨玉龄译. 想像的未来[M]. 台北：天下文化, 1999. 2. 庞秀成、刘莉译. 想像中的世界[M]. 长春：吉林人民出版社, 2001.
1999	The Sun, the Genome and the Internet 出版社：Oxford University Press	1. 席玉苹译. 21世纪三事[M]. 台北：台湾商务印书馆, 1999. 2. 覃方明译. 太阳、基因组与互联网[M]. 北京：三联书店, 2000.
2006	The Scientist as Rebel（戴森书评合集） 出版社：New York Review Books	萧明波、杨光松译. 反叛的科学家[M]. 杭州：浙江大学出版社, 2013.
2007	A Many-Colored Glass 出版社：University of Virginia Press	萧明波、杨光松译. 一面多彩的镜子[M]. 杭州：浙江大学出版社, 2014.
2015	Dreams of Earth and Sky（戴森书评合集） 出版社：New York Review Books	中译本《天地之梦》（待出版），出版社：浙江大学出版社

补充：戴森文章选集（含科学传记与科普内容）

1. Selected Papers of Freeman Dyson with Commentary[M]. Providence: American Mathematical Society (AMS), 1996.
2. Birds and Frogs: Selected Papers, 1990-2014[M]. Singapore: World Scientific, 2015.（含大量科普性文章）

三、参考文献

• [1] 杨振宁. Father and I[M]//C. N. Yang. Selected Papers II With Commentaries. Singapore: World Scientific, 2013.（1991年首次发表）
  中译文：杨振宁. 父亲和我[M]//杨振宁. 曙光集. 北京：三联书店, 2008.

• [2] M. Cook. Faces of Science[M]. New York & London: Norton and Company, 2005.

• [3] E.T. Bell. Men of Mathematics[M]. 1937.
  中译本：
  1. 徐源译. 数学精英（2004年上海科技教育出版社再版更名为《数学大师》）[M]. 北京：商务印书馆, 1991.
  2. 井竹君等译. 大数学家[M]. 台北：九章出版社, 1998.

• [4] G. H. Hardy, E. M. Wright. An Introduction to the Theory of Numbers[M].（D.R. Heath-Brown 与 J.H. Silverman 修订）
  中译本：张明尧、张凡译. 哈代数论[M]. 北京：人民邮电出版社, 2010.

• [5] G. H. Hardy. A Mathematician’s Apology[M].
  中译本：
  1. 王希勇译. 一个数学家的辩白[M]. 北京：商务印书馆, 2007.
  2. 李文林、戴宗铎、高嵘译. 一个数学家的辩白[M]. 大连：大连理工大学出版社, 2014.
  3. 李泳译. 一个数学家的自白[M]. 长沙：湖南科学技术出版社, 2007.

• [6] D. Pedoe. In Love with Geometry[J]. College Mathematics Journal, 1998, 29(3): 170-188.

• [7] C.N. Yang. Selected Papers 1945-1980, with Commentary[M]. San Francisco: W.H. Freeman & Company, 1983.

• [8] 戴森. Chen Ning Yang, A Conservative Revolutionary[M]. 1999.
  中译文：戴森. 杨振宁——保守的革命者[M]//杨振宁. 曙光集. 北京：三联书店, 2008.（2015年4月29日重刊于《中华读书报》）

• [9] 江才健. 戴森：科学是更接近艺术而非哲学[N]. 台湾《中国时报》, 1998-01-30（社会综合版）.

• [10] C.N. Yang. Hermann Weyl’s contribution to physics[M]//C.N. Yang. Selected Papers II With Commentaries. Singapore: World Scientific, 2013.（1985年首次发表）
  中译文：杨振宁. 外尔对物理学的贡献[M]//杨振宁. 曙光集. 北京：三联书店, 2008.

四、作者附语

本文初稿以“弗里曼·戴森：科学家与作家的一生”为题发表于《科学文化评论》2013年第3期；2014年重印于《一面多彩的镜子》中译本附录；2015年刊登于香港《数学文化》第3期；2016年发表于台湾《数理人文》第9期，并将收入即将出版的戴森中译著作《生命起源》。

五、致谢

本文的写作得到以下个人与机构的支持，特此致谢：

1. 清华大学高等研究院杨振宁先生：提供鼓励与支持，并对初稿提出诸多有价值的评论；
2. 弗里曼·戴森：通过邮件提供帮助，包括提供照片、根据英译稿（感谢陈关荣教授润色）指正原文错误；
3. 其他协助者：苏珊·希金斯（S.B. Higgins）女士、江才健先生、陈关荣教授、汤涛教授、丁玖教授、欧阳顺湘教授、葛墨林教授、周坚教授、肖明波教授、张淑娥教授、刘云朋教授、赵振江教授、付晓青教授、崔继峰博士、张海涛博士。

原文出处

• 繁体版：原载于《数理人文》杂志第9期（2016年）；
• 简体版：刊载于“数理人文”微信订阅号；
• 版权说明：未经授权不得转载。

---

via:

• Birds and Frogs - Freeman Dyson _ rtx090200212p.pdf
  https://www.ams.org/notices/200902/rtx090200212p.pdf

• Dyson on Birds and Frogs | Not Even Wrong
  https://www.math.columbia.edu/~woit/wordpress/?p=1506

以下为通知即删系列

• 戴森：鸟与蛙 | 附丘成桐先生缅怀戴森
  https://mp.weixin.qq.com/s/h22c8PWFkp1BOnyps_yhaA

• 戴森传奇——从数论、QED到科普写作大师（上）
  https://mp.weixin.qq.com/s/igmItX34WGu21u4eldTMGw

• 戴森传奇——从数论、QED到科普写作大师（下）
  https://mp.weixin.qq.com/s/hBn7xc_Z4BOlIxB1ph5EHQ