Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:
- the graph contains exactly 2n + p edges;
- the graph doesn't contain self-loops and multiple edges;
- for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.
A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.
Your task is to find a p-interesting graph consisting of n vertices.
The first line contains a single integer t (1 ≤ t ≤ 5)
— the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 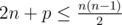 )
— the number of vertices in the graph and the interest value for the appropriate test.
)
— the number of vertices in the graph and the interest value for the appropriate test.
It is guaranteed that the required graph exists.
For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.
Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.
1 6 0
1 2 1 3 1 4 1 5 1 6 2 3 2 4 2 5 2 6 3 4 3 5 3 6
You have an array of positive integers a[1], a[2], ..., a[n] and a set of bad prime
numbers b1, b2, ..., bm.
The prime numbers that do not occur in the set b are considered good. The beauty of
array a is the sum  ,
where function f(s) is determined as follows:
,
where function f(s) is determined as follows:
- f(1) = 0;
-
Let's assume that p is the minimum prime divisor of s.
If p is a good prime, then
 ,
otherwise
,
otherwise  .
.
You are allowed to perform an arbitrary (probably zero) number of operations to improve array a. The operation of improvement is the following sequence of actions:
- Choose some number r (1 ≤ r ≤ n) and calculate the value g = GCD(a[1], a[2], ..., a[r]).
-
Apply the assignments:
 ,
,  , ...,
, ...,  .
.
What is the maximum beauty of the array you can get?
The first line contains two integers n and m (1 ≤ n, m ≤ 5000) showing how many numbers are in the array and how many bad prime numbers there are.
The second line contains n space-separated integers a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — array a. The third line contains m space-separated integers b1, b2, ..., bm (2 ≤ b1 < b2 < ... < bm ≤ 109) — the set of bad prime numbers.
Print a single integer — the answer to the problem.
5 2 4 20 34 10 10 2 5
-2
4 5 2 4 8 16 3 5 7 11 17
10
The sequence of integer pairs (a1, b1), (a2, b2), ..., (ak, bk) is beautiful, if the following statements are fulfilled:
- 1 ≤ a1 ≤ b1 < a2 ≤ b2 < ... < ak ≤ bk ≤ n, where n is a given positive integer;
- all numbers b1 - a1, b2 - a2, ..., bk - ak are distinct.
For the given number n find the number of beautiful sequences of length k. As the answer can be rather large, print the remainder after dividing it by 1000000007 (109 + 7).
The first line contains integer t (1 ≤ t ≤ 2·105) — the number of the test data.
Each of the next t lines contains two integers n and k (1 ≤ k ≤ n ≤ 1000).
For each test from the input print the answer to the problem modulo 1000000007 (109 + 7). Print the answers to the tests in the order in which the tests are given in the input.
6 1 1 2 1 2 2 3 1 3 2 3 3
1 3 0 6 2 0
In the first test sample there is exactly one beautiful sequence: (1, 1).
In the second test sample, the following sequences are beautiful:
- (1, 1);
- (1, 2);
- (2, 2).
In the fourth test sample, the following sequences are beautiful:
- (1, 1);
- (1, 2);
- (1, 3);
- (2, 2);
- (2, 3);
- (3, 3).
In the fifth test sample, the following sequences are beautiful:
- (1, 1), (2, 3);
- (1, 2), (3, 3).
In the third and sixth samples, there are no beautiful sequences.











 本文解析了四道算法竞赛题目,包括构造特定类型的图、优化数组的值、判断矩阵的连通性和计算美观数对的数量。提供了详细的解题思路和算法策略。
本文解析了四道算法竞赛题目,包括构造特定类型的图、优化数组的值、判断矩阵的连通性和计算美观数对的数量。提供了详细的解题思路和算法策略。
















 642
642

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








