SS2LM论文笔记

An Optimal Sphere and Two Large Margins Approach for Novelty Detection(笔记)

  这是硕士期间最早接触的一篇论文，花了比较多的时间。把当年的简要笔记附上来。

上百度学术的超链接

该文章主要是在一篇PAMI上的修改，因此这边也把原文章给附上：

PAMI百度学术原文（A Small Sphere and Large Margin Approach for Novelty Detection Using Training Data with Outliers）

这篇文章首先分析了几种单类分类器，比如OC-SVM, SVDD，SSLM，都是支持向量类型的分类器，通过构造一个分类面（曲面）来分隔正类样本以及负类样本，不过构造方法不大一样。

OCSVM (one class support vector machine)定义了一个超平面来分割正常数据和异常数据同时使得边界值达到最大,通过式子可以看出，与SVM特别相似，只是改造成了只使用单类正样本进行训练，不考虑负类样本，可以通过高维映射的方式扩展为各种高维面作为分割面；

在SVDD(support vector data description)中构造了一个最优超球体来包含所有的正常数据并且保证所有的异常数据都在最优超球体外。

SVDD算是一种比较有特色的SVM变形，与SVM思想不相同的是，SVDD直接构造了一个球体，通过式子可以看出，目标函数是使得球体的半径R最小化，将所有的正类样本包裹在分类面中，那么在外部的肯定就是负类样本。确实，在故障检测或者新奇检测的情况下，正负类样本不均衡的情况中，可能可以轻易获取到很多正类样本，但是负类样本却不一定能够获取得到。在这种情况下无论是采用欠采样或者是过采样的方式都有点不妥，因此直接转换成只对单类样本建模是一种很机智的做法，不过总觉得好歹还是能够获取少数负类样本的，不有效地利用这些负类样本总觉得不太甘心。因此Ye  J等人在PAMI上发表的SSLM的文章就是对少量负类样本利用的方式。

在SSLM(small sphere large margin)中够造了一个最优超球体包含所有的正常数据同时保证该球体和异常数据的距离达到最大。

其中该论文中提出了一个最优超球体和两种数据边界最大化的方法，通过做到两种数据边界最大化，实现正常数据和异常数据间的精度平衡。这个两个边界之间的比例调整将极大地影响整个结果。

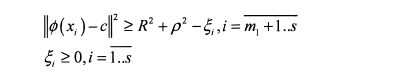
根据SS2LM的论文来看，通过利用少量的样本能够更加精确分类面，不过SS2LM的作者觉得在正负类样本不均衡的情况下，应该对内外间隔进行比例调整，因此在上式中加入了一个小参数进行了改造。

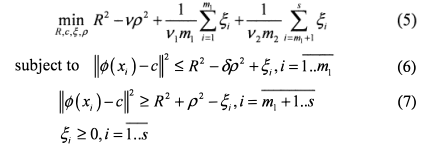
对比SSLM和SS2LM中可以看到，限制条件第一个式子中多了一个参数，用Xi来表示所有的特征数据，其中前m1个数据为正常数据，后m2个数据为异常数据，通过Yi对其进行标记，也就是Y1~Ym1标记为+1，而Ym1+1~Ym1+m2标记为-1，其中R指的是超球面的半径，c指的是超球面的球心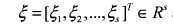，指的是s个松弛变量。其中s=m1+m2也就是样本集的数量。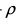指的是外部距离，即判定边界同异常数据的距离。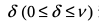指的是外部距离和内部距离的比例。因此，内部距离可以用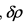进行表示，即判定边界同正常数据的距离。

计算方式类似于SVM的方式，使用的是拉格朗日乘子法。

其中 ，  首先联立两个约束条件为一个，即：

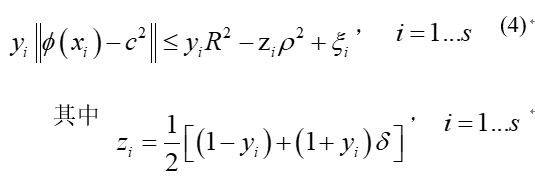
此时，原始的式子就可以写成拉格朗日式的形式了：

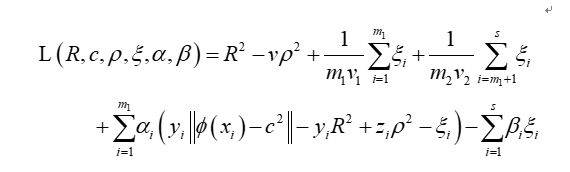
通过拉格朗日式对每个参数进行求导，令导数为0，带入原始式子中，由于符合KKT条件，因此可以转换成下式：

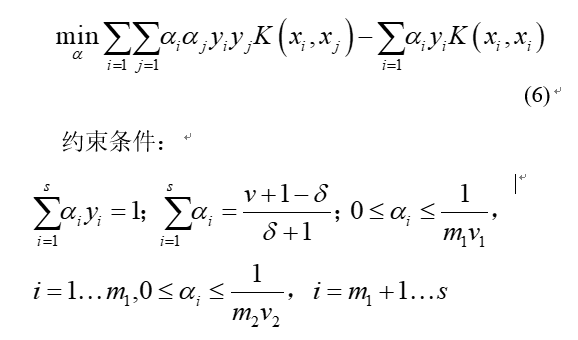
这时候，就转化成一个凸二次优化问题了，论文原文中说的是使用Libsvm里面的工具箱进行求解，通过对C++代码的查看，应该是主要使用里面的solver函数进行相应求解，不过还需要一定的改动，对SMO算法比较熟悉的可以自行了解。一般的方式就是通过SMO算法求解该二次优化问题。最终可以得到一个边界决策函数：

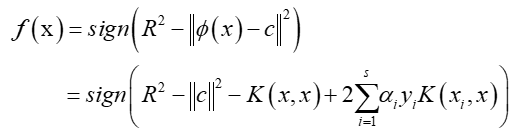
从实验结果来看，该分类器的构造理论完备，实验通过多组不同的实验数据集进行了检验，效果要优于SVM以及SSLM，有很好的应用价值，算是一种比较好的改造。

不过，本人通过改造台湾大学林智仁教授的LIBSVM工具箱，实现了SS2LM和SSLM，发现两个算法在一定的程度上会优于SVM，但是并没有论文的实验结果那么好。在进行检测的时候，虚警率较高，误判比较多，依旧是FP较高。本人研究领域是隐写分析，与故障检测和新奇检测方向有一定的相似，因此对此方面的实验结果有一定的代表性。该分类器较适合用于实验室环境，而实际工程项目中不一定能取得很好的结果。