1. GAN的理论
在图片生成过程中,我们的目标其实是存在一定的分布的,假设在整个图像空间中,蓝色部分的点可以生成人脸,其他区域的脸则不能生成人脸。那么,我们的目的是寻找蓝色区域的概率密度函数

1.1 最大似然估计与GAN
一般的思路是:我们通过sample数据集,去估计给定数据(输入数据)的分布,记为 P d a t a ( x ) P_{data}(x) Pdata(x),因此,使用网络的目的是,找到一堆参数 G G G所构成的分布 P G ( x ; θ ) P_{G}(x;\theta) PG(x;θ)与 P d a t a ( x ) P_{data}(x) Pdata(x)越接近越好。
那么,使用最大似然估计即为:
L
=
∏
i
=
1
m
P
G
(
x
i
,
θ
)
L = \prod_{i=1}^{m}P_G(x^i,\theta)
L=i=1∏mPG(xi,θ)

然后我们在后面减一项,该项与
P
G
(
x
;
θ
)
P_G(x;\theta)
PG(x;θ)没有关系,就变成下面这个式子,就可以整理成KL Divergence的形式。

而Generator的作用就是,将输入映射成各种形状的分布。

那么,在不知道
P
G
P_G
PG和
P
d
a
t
a
P_{data}
Pdata的情况下,怎么样去解这个式子呢?


那么Discriminator的作用是什么呢?其实就是衡量 P G P_G PG和 P d a t a P_{data} Pdata的差别有多大,然后就其实是一个分类的函数

然后得到的最佳的值,其实就是一个JS Divergence的解。当生成数据与原始数据差距很大时,D可以轻易的分辨出来,否则的话,D很难分辨出来。

1.2 数学推导

考虑到sample 出来的每一个样本都是独立的,于是可以把这个积分拆开来计算,即要优化下面的式子:






所以,现在问题就可以变成下面这个式子:
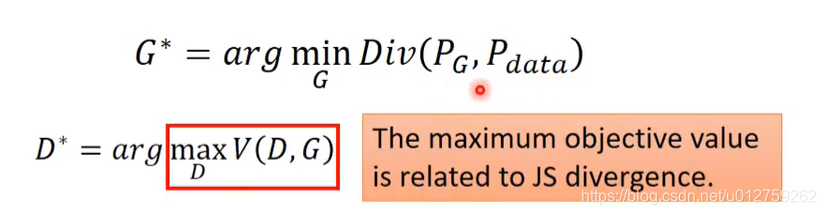


G3是最好的选择,因为满足
arg min
G
\argmin_G
Gargmin要求蓝色的线最小,而
max
D
\max_D
maxD代表红色的点。

同理,对于
L
(
G
)
L(G)
L(G)也是一样的。那么,在第一次迭代之后,得到
G
0
G_0
G0之后,我们需要找到
D
0
∗
D_0^*
D0∗使得
V
(
G
0
,
D
)
V(G_0,D)
V(G0,D)最大(对应图中的红点)。

然后当我们更新了
G
G
G变成
G
1
G_1
G1之后,我们需要重新找一个
D
D
D来满足要求。但是这样的有一个前提假设
D
0
∗
≈
D
1
∗
D_0^* \approx D_1^*
D0∗≈D1∗。
在训练过程中要更新
G
G
G所以
V
(
G
,
D
)
V(G,D)
V(G,D)的分布形状也会发生改变,因此,
V
(
G
,
D
)
V(G,D)
V(G,D)在
G
G
G的变化过程中不会发生太大的改变,也就是说,我们在训练过程中,对于G,不能训练的太多(不能让他们的分布形状变化太多)而对于D来说,我们需要训练到底,因为我们要求最大值。
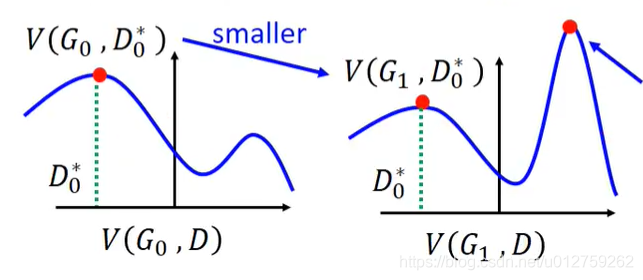

1.3 算法
D 最好能够多train几次,

G不能多train,否则的话找的divergence就不是原来D中对应的那个divergence。

在GAN的论文中提到,一开始,我们的优化目标应该是
log
(
1
−
D
(
G
(
z
i
)
)
)
\log(1-D(G(z^i)))
log(1−D(G(zi))),但是考虑到他的趋势一开始微分的结果非常小,所以在训练的过程中会出现一些问题

于是,优化的目标函数就变成了相同趋势的
−
log
(
D
(
x
)
)
-\log(D(x))
−log(D(x)):


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








