相信关于混淆矩阵、ROC和AUC的问题一直困扰着大家,要想搞懂ROC和AUC,首先要明白混淆矩阵是什么。
混淆矩阵
混淆矩阵中有着Positive、Negative、True、False的概念,其意义如下:
- 称预测类别为1的为Positive(阳性),预测类别为0的为Negative(阴性)。
- 预测正确的为True(真),预测错误的为False(伪)。
对上述概念进行组合,就产生了如下的混淆矩阵:

由此引出True Positive Rate(真阳率)、False Positive(伪阳率)两个概念:
仔细看这两个公式,发现其实TPR就是TP除以TP所在的列,FPR就是FP除以FP所在的列,二者意义如下:
- TPR的意义是所有真实类别为1的样本中,预测类别为1的比例。
- FPR的意义是所有真是类别为0的样本中,预测类别为1的比例。
如果上述概念都弄懂了,那么ROC曲线和AUC就比较容易理解了:
AUC是一个模型评价指标,只能用于二分类模型的评价,对于二分类模型,还有很多其他评价指标,比如accuracy,precision。
为什么AUC比accuracy更常用呢?因为很多机器学习的模型对分类问题的预测结果都是概率,如果要计算accuracy,需要先把概率转化成类别,这就需要手动设置一个阈值,如果对一个样本的预测概率高于这个预测,就把这个样本放进一个类别里面,低于这个阈值,放进另一个类别里面。所以这个阈值很大程度上影响了accuracy的计算。
AUC的本质含义反映的是对于任意一对正负例样本,模型将正样本预测为正例的可能性 大于 将负例预测为正例的可能性的 概率,是Area under curve的首字母缩写。Area under curve是什么呢,从字面理解,就是一条曲线下面区域的面积。所以我们要先来弄清楚这条曲线是什么。这个曲线有个名字,叫ROC曲线。ROC曲线是基于样本的真实类别和预测概率来画的,具体来说,ROC曲线的x轴是伪阳率(false positive rate),y轴是真阳率(true positive rate)。即ROC曲线的横轴是FPRate,纵轴是TPRate,当二者相等时,即y=x,如下图,表示的意义是:
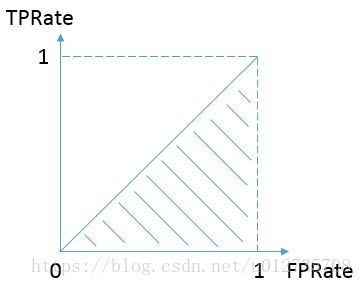
对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。
而我们希望分类器达到的效果是:对于真实类别为1的样本,分类器预测为1的概率(即TPRate),要大于真实类别为0而预测类别为1的概率(即FPRate)。这样的ROC曲线是在y=x之上的,因此大部分的ROC曲线长成下面这个样子:
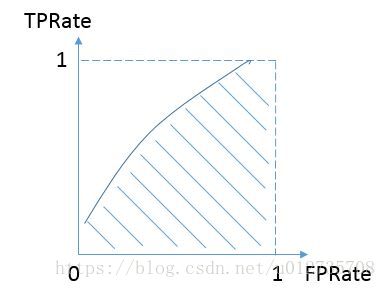
那么,最理想的情况下没有真实类别为1而错分为0的样本,TPRate一直为1,于是AUC为1,这便是AUC的极大值。
说了这么多还是不够直观,不妨举个简单的例子。
首先对于硬分类器(例如SVM,NB),预测类别为离散标签,对于8个样本的预测情况如下:

得到混淆矩阵如下:
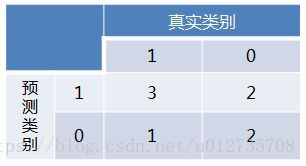
此时,TP=3,FP=2,TN=1,FN=2,由TPRate=TP/(TP+FN),FPRate=FP/(FP+TN)
进而算得TPRate=3/4,FPRate=2/4,得到ROC曲线:
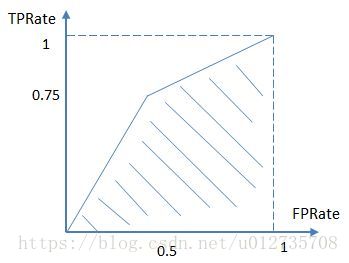
最终得到AUC为0.625。
对于LR等预测类别为概率的分类器,依然用上述例子,假设预测结果如下:

这时,需要设置阈值来得到混淆矩阵,不同的阈值会影响得到的TPRate,FPRate,如果阈值取0.5,小于0.5的为0,否则为1,那么我们就得到了与之前一样的混淆矩阵。其他的阈值就不再啰嗦了。依次使用所有预测值作为阈值,得到一系列TPRate,FPRate,描点,求面积,即可得到AUC。
AUC的优势,AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
例如在反欺诈场景,设非欺诈类样本为正例,负例占比很少(假设0.1%),如果使用准确率评估,把所有的样本预测为正例便可以获得99.9%的准确率。
但是如果使用AUC,把所有样本预测为正例,TPRate和FPRate同时为1,AUC仅为0.5,成功规避了样本不均匀带来的问题。
使用python计算AUC的代码:
from sklearn import metrics
def AUC():
fpr,tpr,thresholds=metrics.roc_curve(act,pred,pos_label=1)
return metrics.auc(fpr,tpr)说了半天,大家可能还是不太清楚,下面咱们通过一个python写的例子加深下理解。
假设我们通过训练集训练了一个二分类模型,在测试集上进行预测每个样本所属的类别,输出了属于类别”1“的概率。现在假设当P>=0.5时(threshold=0.5),预测的类标签为”1“。
(1)导入相关库
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
#生成测试样本的数量
parameter=50(2)随机生成结果集
data=pd.DataFrame(index=range(0,parameter),columns=('probability','The true label'))
data['The true label']=np.random.randint(0,2,size=len(data))
data['probability']=np.random.choice(np.arange(0.1,1,0.1),len(data['probability']))
生成数据为:
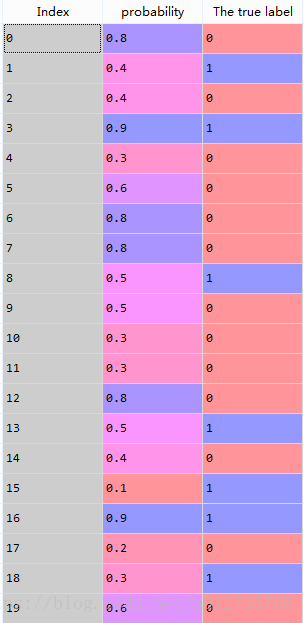
(3)计算混淆矩阵
cm=np.arange(4).reshape(2,2)
cm[0,0]=len(data[(data['The true label']==0)&(data['probability']<0.5)]) #TN
cm[0,1]=len(data[(data['The true label']==0)&(data['probability']>=0.5)])#FP
cm[1,0]=len(data[(data['The true label']==1)&(data['probability']<0.5)]) #FN
cm[1,1]=len(data[(data['The true label']==1)&(data['probability']>=0.5)])#TP
(4)计算假正率和真正率
首先,画出混淆矩阵。
import itertools
classes = [0,1]
plt.figure()
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion matrix')
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],horizontalalignment="center", color="red" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show() 生成的混淆矩阵如下所示:
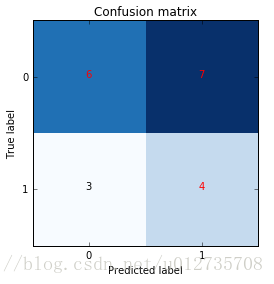
然后,threshold=0.5上的假正率和真正率容易计算,为: FPR=7/(7+6)=0.54,TPR=4/(4+3)=0.57
ROC曲线和AUC值
ROC曲线是一系列threshold下的(FPR,TPR)数值点的连线。此时的threshold的取值分别为测试数据集中各样本的预测概率。但,取各个概率的顺序是从大到小的。
(1)按概率值排序
首先,按预测概率从大到小的顺序排序:
data.sort_values('probability',inplace=True,ascending=False)排序结果如下:
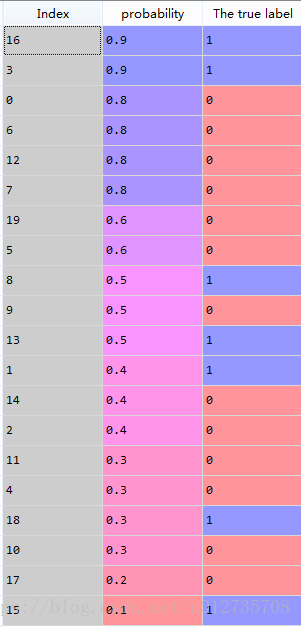
此时,threshold依次取0.9,0.9,0.8,0.8,0.8,0.8,0.6,0.6...。 比如,当threshold=0.9(第2个0.9),两个”1“预测正确,FPR=1/11=0,TPR=2/7=0.286。 当threshold=0.8(第3个0.8),三个”0“预测错误,两个”1“预测正确,FPR=3/11=0.231,TPR=2/7=0.286。
(2)计算全部概率值下的FPR和TPR
TPRandFPR=pd.DataFrame(index=range(len(data)),columns=('TP','FP'))
for j in range(len(data)):
data1=data.head(n=j+1)
FP=len(data1[data1['The true label']==0])/float(len(data[data['The true label']==0]))
TP=len(data1[data1['The true label']==1])/float(len(data[data['The true label']==1]))
TPRandFPR.iloc[j]=[TP,FP]最后,(FPR,TPR)点矩阵如下:
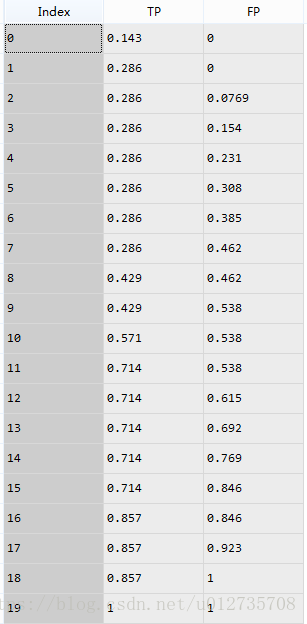
(3)画出最终的ROC曲线和计算AUC值
from sklearn.metrics import auc
AUC= auc(TPRandFPR['FP'],TPRandFPR['TP'])
plt.scatter(x=TPRandFPR['FP'],y=TPRandFPR['TP'],label='(FPR,TPR)',color='k')
plt.plot(TPRandFPR['FP'], TPRandFPR['TP'], 'k',label='AUC = %0.2f'% AUC)
plt.legend(loc='lower right')
plt.title('Receiver Operating Characteristic')
plt.plot([(0,0),(1,1)],'r--')
plt.xlim([-0.01,1.01])
plt.ylim([-0.01,01.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
下图的黑色线即为ROC曲线,测试样本中的数据点越多,曲线越平滑:
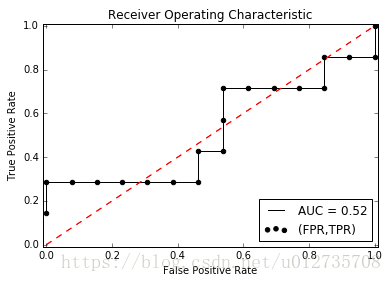
AUC(Area Under roc Cure),顾名思义,其就是ROC曲线小的面积,在此例子中AUC=0.52。AUC越大,说明分类效果越好。
当我们增加测试样本的数量时(parameter=10000),得到的ROC和AUC如下图所示:
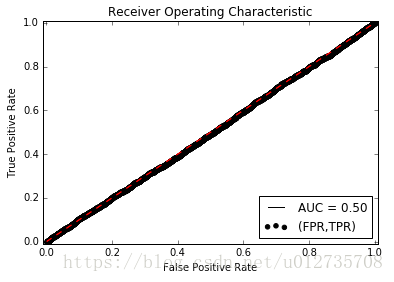
由图可以看出此时ROC和y=x基本重合,AUC=0.5,这是因为我们随机生成的测试数据,基本上和猜没啥区别了,判断对和错的概率各占一半。
补充:
当然,针对上面混淆矩阵我们可以换一种更形象的图例进行记忆,如下图所示:
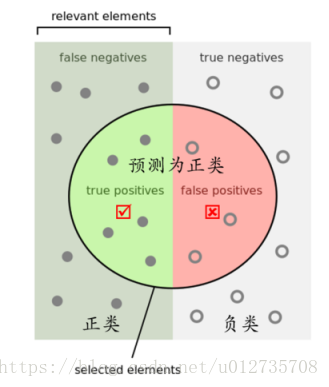

PS.P和R指标(即精确率和召回率)有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score)。
F-Measure是Precision和Recall加权调和平均,我们常用的是F1指标,即α=1的情况。
本文旨在初步理解混淆矩阵、ROC和AUC,并通过python例子加深对概念的认识,希望对小伙伴们有帮助。
参考文献:
https://www.jianshu.com/p/c61ae11cc5f6
https://www.zhihu.com/question/39840928?from=profile_question_card
李航. 统计学习方法[M]. 清华大学出版社, 2012.





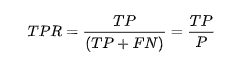
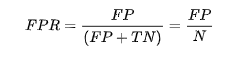
















 2320
2320

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








