v_3_线性回归L1与L2正则化

机器学习监督算法的基本思路是 让拟合的模型尽量接近真实数据 。在这个过程可能存在两个截然相反的问题：过拟合和欠拟合。欠拟合是模型预测值与真实值之间误差较大，梯度下降就是讨论解决问题（求损失函数最小）。
而正则化则是探讨过拟合的问题。正则化通过降低模型的复杂性，达到避免过拟合的问题。

损失函数后面会添加一个额外项，常用的额外项一般有两种：L1正则化和L2正则化。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

结论:
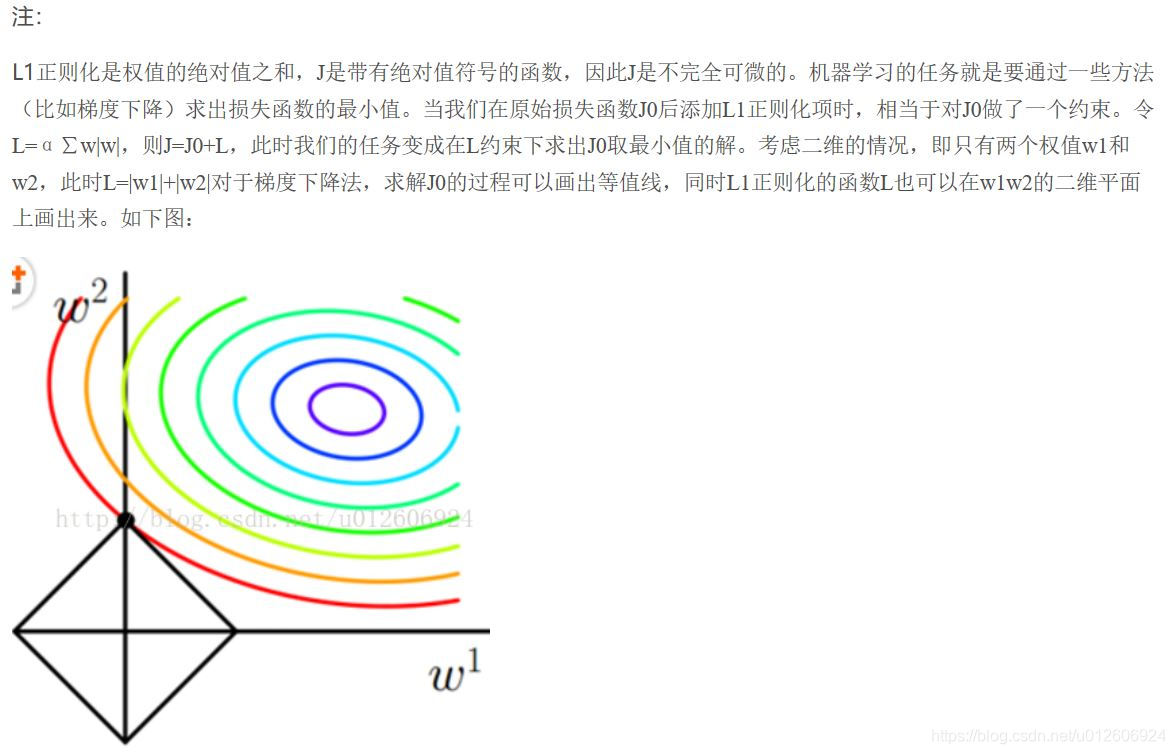
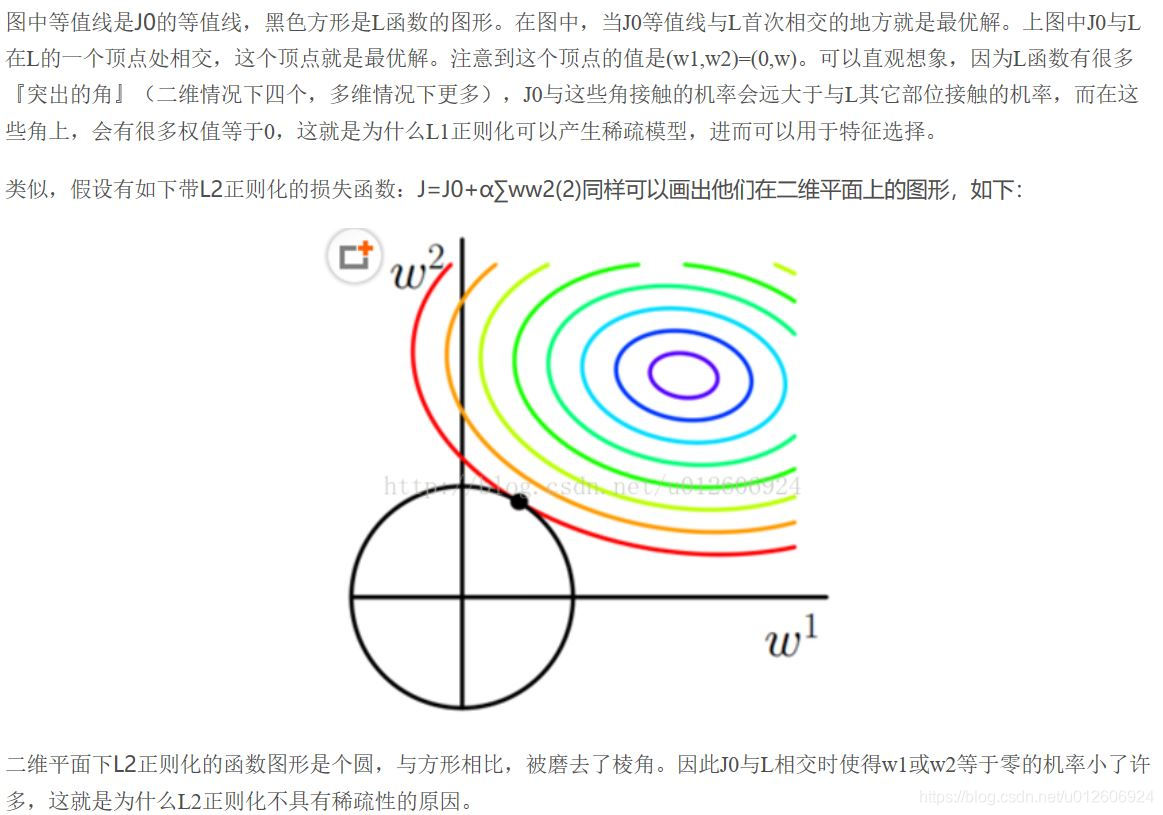
L1正则化和L2正则化：L1正则化就是在loss function后边所加正则项为L1范数，加上L1范数容易得到稀疏解（0比较多）。L2正则化就是loss function后边所加正则项为L2范数的平方，加上L2正则相比于L1正则来说，得到的解比较平滑（不是稀疏），但是同样能够保证解中接近于0（但不是等于0，所以相对平滑）的维度比较多，降低模型的复杂度。L1与L2解决过拟合几何原理
1. L2 regularizer ：使得模型的解偏向于 norm较小的 W，通过限制W 的norm 的大小实现了对模型空间的限制，从而在一定程度上避免了overfitting 。不过ridge regression 并不具有产生稀疏解的能力，得到的系数 仍然需要数据中的所有特征才能计算预测结果，从计算量上来说并没有得到改观。
2. L1 regularizer ： 它的优良性质是能产生稀疏性，导致 W中许多项变成零。 稀疏的解除了计算量上的好处之外，更重要的是更具有“可解释性”。