5-1 线性回归算法

1. 线性回归算法简介

线性回归算法的特点

• 解决回归问题
• 思想简单,容易实现
• 许多强大的非线性模型的基础  (逻辑回归\多项式回归\SVM等)
• 结果具有很好的可解释性
• 蕴含机器学习中的很多重要思想

分类问题和回归问题的区别

分类问题,坐标轴都是特征, 颜色代表样本的输出标记(离散)

回归问题,横轴是特征,纵轴是样本的输出标记,样本的输出标记在一个连续的空间里

简单线性回归的思想(拟合方程\损失函数)

简单线性回归(只有一个特征)

多个特征是多元线性回归

总体思想: 找到一组参数值使得某个函数(损失函数)尽可能的小

[机器学习中的参数学习算法就是创建一个模型, 然后学习模型的参数===>找到这些参数使得可以最优化损失函数

 近乎所有参数学习算法都是这样的套路

模型不同, 建立的目标函数不同, 优化的方式不同]

简单线性回归通过最小二乘法最优化损失函数

a,b表达式的具体推导过程: 用最小二乘法求解参数a, b(分别对每个参数求偏导数,并另偏导数=0)

更改成更容易提高计算效率的形式(利用)

---

2. 实现简单线性回归算法

与KNN.py不同的是, 简单线性回归不需要保存X_train和y_train,只需要保存根据用户传入的训练集计算出的模型参数

predict的时候只需要参数即可

import numpy as np

class SimpleLinearRegression1:

    def __init__(self):
        """初始化模型"""
        self.a_ = None
        self.b_ = None



    def fit(self, x_train, y_train):
        """根据训练集数据训练模型"""
        assert x_train.ndim == 1
        assert len(x_train) == len(y_train)

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0

        for x, y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict, 返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1
        assert self.a_ is not None and self.b_ is not None

        return np.array([self.predict(x_single) for x_single in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        """object 类提供的 __repr__() 方法总是返回该对象实现类的“类名+object at+内存地址”值，这个返回值并不能真正实现“自我描述”的功能，因此，如果用户需要自定义类能实现“自我描述”的功能，就必须重写 __repr__() 方法"""
        return "simplelinearregression1()"

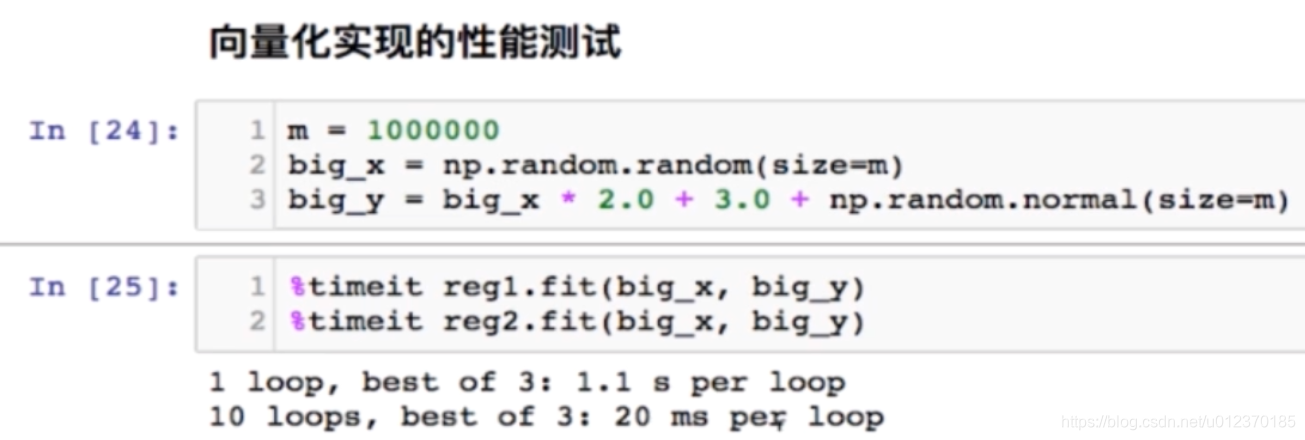
向量化运算

不使用for循环

import numpy as np

class SimpleLinearRegression2:

    def __init__(self):
        """初始化模型"""
        self.a_ = None
        self.b_ = None



    def fit(self, x_train, y_train):
        """根据训练集数据训练模型"""
        assert x_train.ndim == 1
        assert len(x_train) == len(y_train)

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = (x_train - x_mean).dot(y_tain - y_mean)
        d = (x_train - x_mean).dot(x_train - x_mean)

        #for x, y in zip(x_train, y_train):
        #   num += (x - x_mean) * (y - y_mean)
        #   d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict, 返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1
        assert self.a_ is not None and self.b_ is not None

        return np.array([self.predict(x_single) for x_single in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        """object 类提供的 __repr__() 方法总是返回该对象实现类的“类名+object at+内存地址”值，这个返回值并不能真正实现“自我描述”的功能，因此，如果用户需要自定义类能实现“自我描述”的功能，就必须重写 __repr__() 方法"""
        return "simplelinearregression1()"