目录
常见的机器学习算法:
机器学习算法(一)—决策树
机器学习算法(二)—支持向量机SVM
机器学习算法(三)—K近邻
机器学习算法(四)—集成算法
基于XGBoost的集成学习算法
基于LightGBM的集成学习算法
机器学习算法(五)—聚类
机器学习算法(六)—逻辑回归
机器学习算法(七)—Apriori 关联分析
机器学习算法(八)—朴素贝叶斯
九种降维方法汇总
一、Kmeans聚类
kmeans算法原理:最小化所有样本到所属类别中心的(欧氏)距离平方和(误差平方和SSE),采用迭代的方式实现收敛。kmeans对初始条件比较敏感,可多次给定不同的初始条件计算,最后选择最小的那一组作为最终结果。kmeans用质心定义原型,其中质心是一组点的均值。
聚类和分类的区别:
- 聚类(Clustering):是指把相似的数据划分到一起,具体划分的时候并不关心这一类的标签,目标就是把相似的数据聚合到一起。
- 分类(Classification):是把不同的数据划分开,其过程是通过训练数据集获得一个分类器,再通过分类器去预测未知数据。
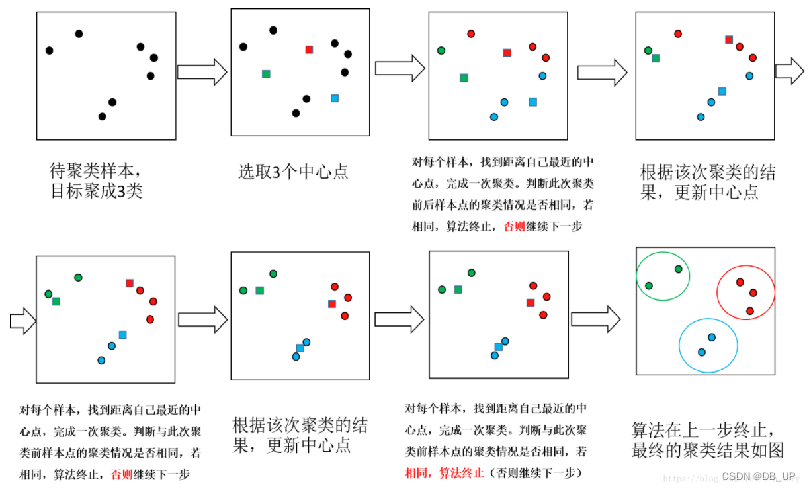
1.1 kmeans算法步骤
- 1.选择k个点作为初始质心
- 2.将每个点指派到最近的质心,形成k个簇,通过采用欧氏距离和余弦距离(先标准化)
- 3.重新计算每个簇的质心
- 4.重复第2和第3步,直到质心不发生变化
1.2 kmeans算法损失函数

1.3 k值的选取
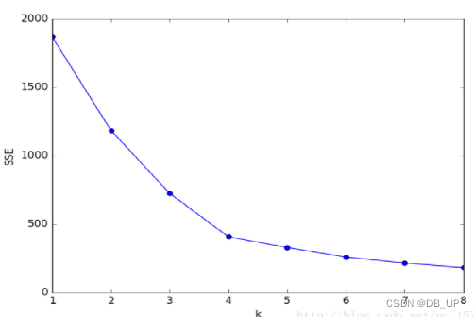
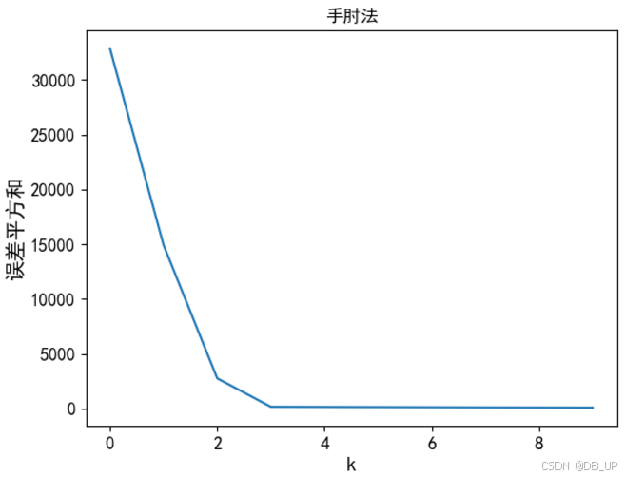
1.手肘法
核心指标是:SSE(误差平方和)
核心思想:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么SSE自然会逐渐减小,并且,当k小于真实聚类时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k达到真实聚类时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降会骤减,随着k值的增大而趋于平缓.
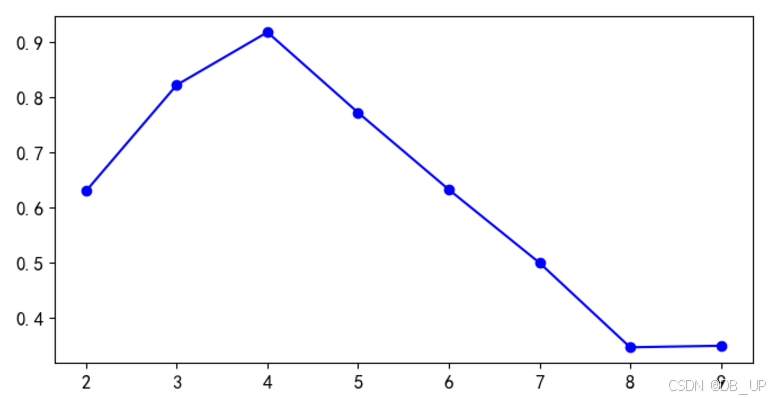
2.轮廓系数
结合类内聚合度和类间分离度两种指标来计算得到
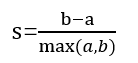
a:x与同簇其他样本的平均距离
b:x与最近簇中所有样本的平均距离
s 越接近1,聚类合理
s接近-1,更适合聚其他类
s接近0,i在两个簇边界上
1.4 kmeans优缺点
优点:
- 1.原理简单,实现也容易,收敛速度快
- 2.聚类效果较优
- 3.算法的可解释性较强
- 4.需要调整的参数仅仅为簇数k
缺点: - 1.k值的选取不好把握,受初值影响
- 2.不能处理非球型簇、不同尺寸和不同密度的簇
- 3.对噪声和异常值比较敏感
- 4.采用迭代方法,得到的结果只是局部最优
1.5 kmeans与knn区别
- kmeans 是无监督学习的聚类算法,没有样本输出
- knn是监督学习的分类算法,有对应类别输出,knn基本不需要训练,对测试集里的点,只需要找到在训练集中最近的k个点,用这最近的k个点的类别来决定测试点的类别
- kmeans则有明显的训练过程,找到k个类别的最佳质点,从而决定样本的簇类别
1.6 kmeans算法案例
#kmeans聚类
import numpy as np
import pandas as pd
import os
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize']=14
plt.rcParams['xtick.labelsize']=12
plt.rcParams['ytick.labelsize']=12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
from sklearn.datasets import make_blobs #make_blobs生成聚类数据集
#centers:聚类中心的个数,可以理解为 label 的种类数n_features:样本维度,cluster_std:数据集的标准差,默认值 1.0
x,y=make_blobs(n_samples=500,n_features=2,centers=4,cluster_std=0.4,random_state=42)
plt.scatter(x[:,0],x[:,1],c=y)
plt.show()
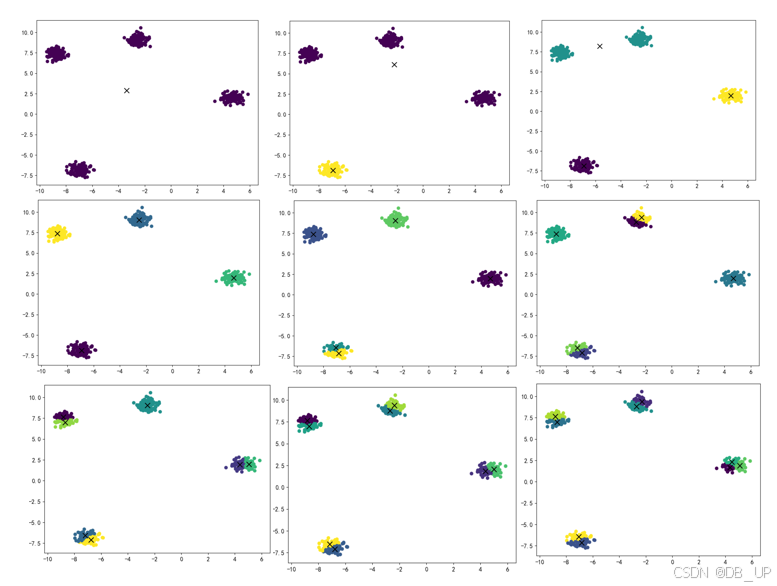
# 1、使用手肘法确认 k-means 算法最优参数
k = np.arange(1, 11)
inertia = []
for i in k:
model = KMeans(n_clusters=i)
model.fit(x)
inertia.append(model.inertia_)
y_pre = model.predict(x)
centroid = model.cluster_centers_
# 绘制当前模型下的聚类中心
plt.figure(figsize=(8,6))
plt.scatter(x[:, 0], x[:, 1], c=y_pre)
plt.scatter(centroid[:, 0], centroid[:, 1], marker='x', s=100, c='black')
plt.show()
# 绘制样本离最近聚类中心距离总和(inertias)
plt.figure()
plt.plot(inertia)
plt.xlabel('k')
plt.ylabel('误差平方和')
plt.title('手肘法')
plt.show()
#2、使用轮廓系数
from sklearn.metrics import silhouette_score #加载轮廓系数
silhouette_score(X,kmeans.labels_)
kmeans_per_k=[KMeans(n_clusters = k).fit(x) for k in range(1, 10)]
silhouette_scores=[silhouette_score(X,model.labels_) for model in kmeans_per_k[1:]]
silhouette_scores
plt.figure(figsize=(8,4))
plt.plot(range(2,10),silhouette_scores,"bo-")
plt.show()
Attributes:属性
cluster_centers_:保存每个簇的中心点(质心)坐标
labels_:存储每个样本所属的簇标签
inertia_:每个样本到中心点最近的距离和
n_iter_:算法执行的迭代次数,表示从初始化到达到收敛所需的迭代总次数。
n_features_in_:输入数据中特征的数量,表示模型训练时使用的特征维度
feature_names_in_:输入数据中每个特征的名称
Methods:方法
fit:对输入数据进行聚类训练
fit_predict:对数据进行聚类训练,同时返回每个样本的簇标签
fit_transform:对数据进行聚类训练,并返回每个样本到其簇中心的距离
get_feature_names_out:返回处理后的特征名称,适合与特征管道集成
get_params:获取模型的超参数配置,返回一个字典,包括初始化时的参数设置
predict:根据已经训练好的模型,预测输入数据 X 中每个样本的簇标签。适合新数据分类。
score:评估模型的性能,通常返回负的 inertia_ 值。可以作为衡量聚类质量的指标。
transform:计算输入数据到各个簇中心的距离矩阵
set_fit_request:设置与训练相关的配置信息,用于自定义数据输入的元数据行为。
set_output:控制输出数据的格式,例如返回 NumPy 数组或 pandas DataFrame。适合与管道集成。
set_params:设置模型的超参数配置,允许通过字典形式更新 KMeans 的参数。
set_score_request:设置与评分相关的元数据行为,用于调整 score 方法的输出格式。
1.7 kmeans存在的问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 数据生成和绘制函数
def plot_data(X):
plt.scatter(X[:, 0], X[:, 1], alpha=0.6)
plt.show()
# 数据准备
x1, y1 = make_blobs(n_samples=1000, centers=((4, -4), (0, 0)), random_state=42)
x1 = x1.dot(np.array([[0.374, 0.95], [0.732, 0.598]]))
x2, y2 = make_blobs(n_samples=250, centers=1, random_state=42)
x2 = x2 + np.array([6, -8])
X = np.r_[x1, x2]
y = np.r_[y1, y2]
# 绘制原始数据分布
plot_data(X)
# 设置 KMeans 模型
kmeans_good = KMeans(n_clusters=3, init=np.array([[-1.5, 2.5], [0.5, 0], [4, 0]]), n_init=1, random_state=42)
kmeans_bad = KMeans(n_clusters=3, random_state=42)
# 模型训练
kmeans_good.fit(X)
kmeans_bad.fit(X)
# 计算inertias
good_inertias = kmeans_good.inertia_
bad_inertias = kmeans_bad.inertia_
# 创建子图展示两种模型的结果
fig, axes = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)
# kmeans_good 聚类结果
axes[0].scatter(X[:, 0], X[:, 1], c=kmeans_good.labels_, cmap='viridis', alpha=0.6)
axes[0].scatter(kmeans_good.cluster_centers_[:, 0], kmeans_good.cluster_centers_[:, 1], s=200, c='red', marker='X')
axes[0].set_title(f'Good Initialization\nInertia: {good_inertias:.2f}')
# kmeans_bad 聚类结果
axes[1].scatter(X[:, 0], X[:, 1], c=kmeans_bad.labels_, cmap='viridis', alpha=0.6)
axes[1].scatter(kmeans_bad.cluster_centers_[:, 0], kmeans_bad.cluster_centers_[:, 1], s=200, c='red', marker='X')
axes[1].set_title(f'Bad Initialization\nInertia: {bad_inertias:.2f}')
plt.tight_layout()
plt.show()
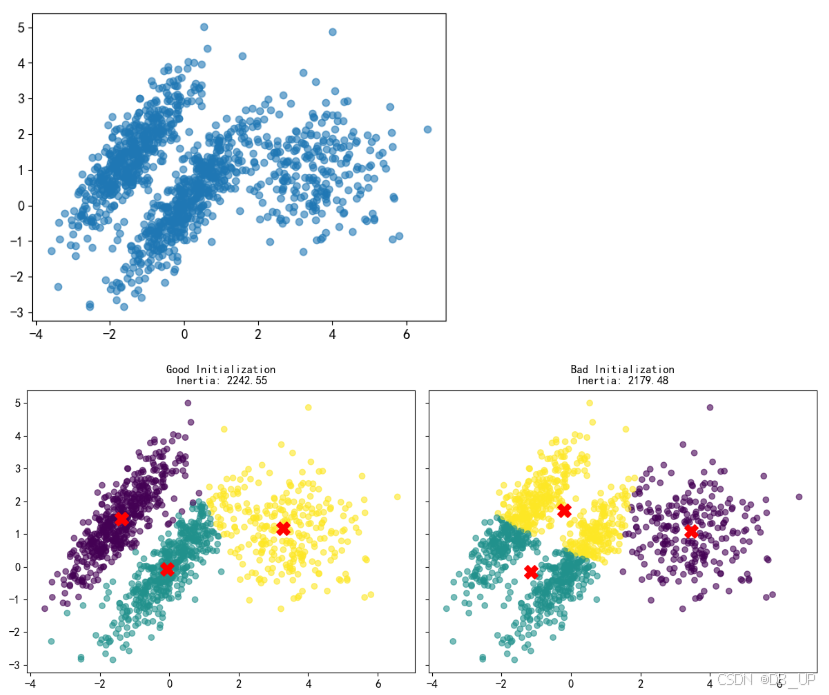
从Good Initialization图中看出inertias大于Bad Initialization,实际Good Initialization聚类效果要好,因此评估标准只能当作一个参考。
二、DBSCAN密度聚类
DBSCAN为密度聚类方法,为了克服基于距离算法只能发现凸的聚类的缺点,可以发现任意形状聚类,且对噪声数据不敏感。如果样本点密度大于某个阈值,可以把样本添加到最近的簇中。
典型案例:有营销活动送一些礼品套件,其中恶意用户来利用这个活动频繁刷取这些套件,我们需要智能识别出这些用户,将其和正常用户区别开来。观察这些恶意刷取套件的用户id存在高密度聚合,在这个情况下DBSCAN可以较好的利用密度聚类把恶意用户聚集起来。
2.1 DBSCAN算法步骤
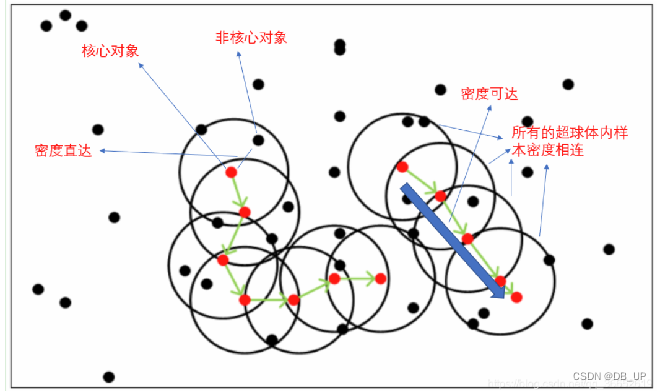
基本概念:
核心对象:若某个点的密度达到算法设定的阈值则其为核心点。(即r邻域内点的数量不小于 minPts)
密度直达:若某点p在点q的r邻域内,且q是核心点则 p-q 直接密度可达
密度可达:若有一个点的序列q0、q1、….qk,对任意 qi-qi-1 是直接密度可达的则称从 q0 到 qk 密度可达,这实际上是直接密度可达的“传播”。
e-邻域的距离阈值:设定的半径r
密度相连:若从某核心点p出发,点q和点k都是密度可达的,则称点q和点k是密度相连的。
边界点:属于某一个类的非核心点,不能发展下线了
噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
算法工作流程:
- 1、定义关键参数:
ϵ (eps):定义在某点周围形成密度区域的半径。
MinPts:定义形成密度区域的最小样本点数。 - 2、算法执行步骤:
Step 1: 从数据集中任意选择一个未访问的点 P。
Step 2: 找到 P 的 ϵ-邻域中的所有点。 - 如果点的邻域样本点数大于或等于 MinPts,将其标记为核心点。
- 如果小于 MinPts,则将其标记为噪声点或后续检查时变为边界点。
Step 3: 从核心点开始扩展形成聚类 - 将核心点的所有邻域点加入当前聚类。
- 对每个邻域中的核心点重复扩展,直到不能再扩展为止。
Step 4: 标记已经处理过的点,避免重复计算。
Step 5: 重复上述步骤,直到所有点都被访问。
2.2 DBSCAN参数选择
半径ϵ,可以根据K距离来设定:找突变点
K距离:给定数据集P={p(i); i=0,1…n},计算点P(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。
MinPts:k-距离中k的值,一般取的小一些,多次尝试
2.3 DBSCAN算法优缺点
DBSCAN算法优点:
- 1.可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
- 2.可以在聚类的同时发现异常点,对数据集中的异常点不敏感
- 3.评估方法聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN算法缺点: - 1.如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
- 2.调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
- 3.如果样本集较大时,聚类收敛时间较长
2.4 DBSCAN算法案例
import numpy as np
import pandas as pd
from sklearn.datasets import make_moons
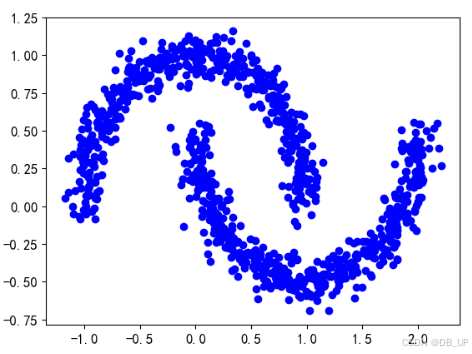
x,y=make_moons(n_samples=1000,noise=0.08,random_state=42)
plt.plot(x[:,0],x[:,1],'bo')
from sklearn.cluster import DBSCAN
dbscan=DBSCAN(eps=0.05,min_samples=5)
y_pred=dbscan.fit_predict(x)
print(dbscan.labels_)
print(dbscan.core_sample_indices_) #核心对象索引
np.unique(dbscan.labels_) #类别个数
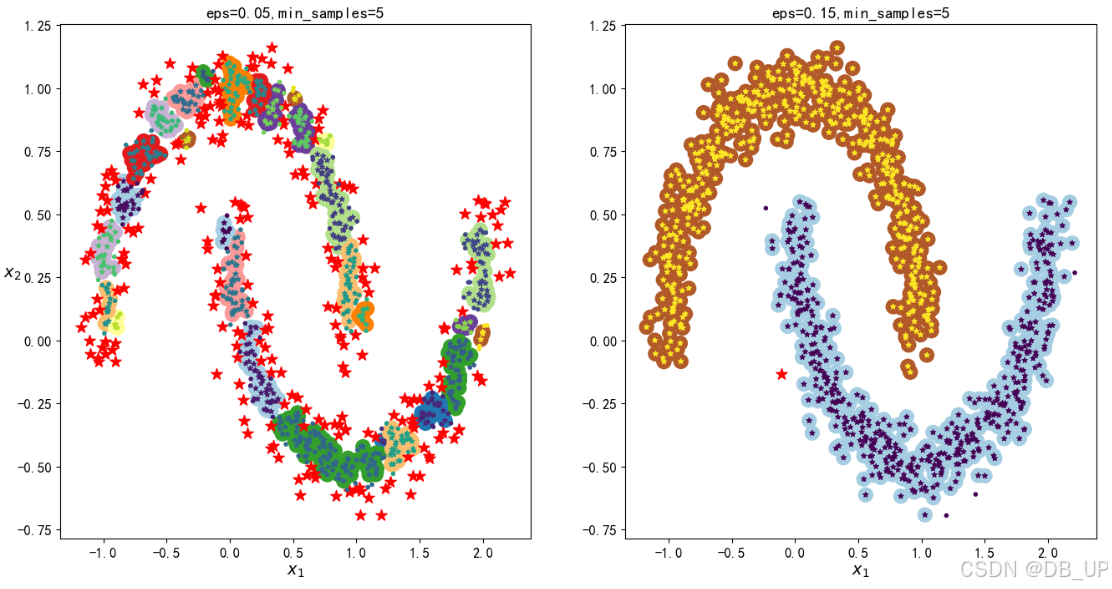
from sklearn.cluster import DBSCAN
dbscan=DBSCAN(eps=0.05,min_samples=5)
y_pred=dbscan.fit_predict(x)
print(dbscan.labels_)
print(dbscan.core_sample_indices_)
dbscan2=DBSCAN(eps=0.2,min_samples=5)
y_pred2=dbscan2.fit_predict(x)
def plot_dbscan(dbscan,x,size,show_xlabels=True,show_ylabels=True):
#dbscan:传入已经拟合的 DBSCAN 模型对象。
#x:数据集,包含需要可视化的二维数据点。
#size:设置聚类点的大小。
#show_xlabels 和 show_ylabels:控制是否显示 x 轴和 y 轴标签。
core_mask=np.zeros_like(dbscan.labels_,dtype=bool)
core_mask[dbscan.core_sample_indices_]=True #创建核心点掩码 core_mask
anomalies_mask=dbscan.labels_==-1 #创建噪声点掩码 anomalies_mask
non_core_mask=~(core_mask|anomalies_mask) #创建非核心点掩码 non_core_mask
cores=dbscan.components_ #提取核心点的坐标 cores
anomalies_mask=x[anomalies_mask] #提取噪声点和非核心点的坐标
non_core=x[non_core_mask]
plt.scatter(cores[:,0],cores[:,1],c=dbscan.labels_[core_mask],marker='o',s=size,cmap='Paired')
#使用 scatter 绘制核心点,标记为圆点(marker='o')
plt.scatter(cores[:,0],cores[:,1],marker='*',s=20,c=dbscan.labels_[core_mask])
#绘制核心点标记,在核心点上再绘制一层星号(marker='*')
plt.scatter(anomalies_mask[:,0],anomalies_mask[:,1],c='r',marker='*',s=100)
#使用红色(c='r')星号(marker='*')标记噪声点。
plt.scatter(non_core[:,0],non_core[:,1],c=dbscan.labels_[non_core_mask],marker='.')
#使用点状标记(marker='.')绘制非核心点。
if show_xlabels:
plt.xlabel("$x_1$",fontsize=14) #如果 show_xlabels=True,显示 x 轴标签 $x_1$。否则,关闭 x 轴标签显示。
else:
plt.tick_params(labelbottom='off')
if show_ylabels: #如果 show_ylabels=True,显示 y 轴标签 $x_2$。否则,关闭 y 轴标签显示。
plt.ylabel("$x_2$",fontsize=14,rotation=0)
else:
plt.tick_params(labelleft='off')
plt.title("eps={:.2f},min_samples={}".format(dbscan.eps,dbscan.min_samples),fontsize=14) #显示 DBSCAN 模型的参数𝜖和 min_samples
plt.figure(figsize=(16,8))
plt.subplot(121)
plot_dbscan(dbscan,x,size=150)
plt.subplot(122)
plot_dbscan(dbscan2,x,size=150,show_ylabels=False)
plt.show()
三、层次聚类
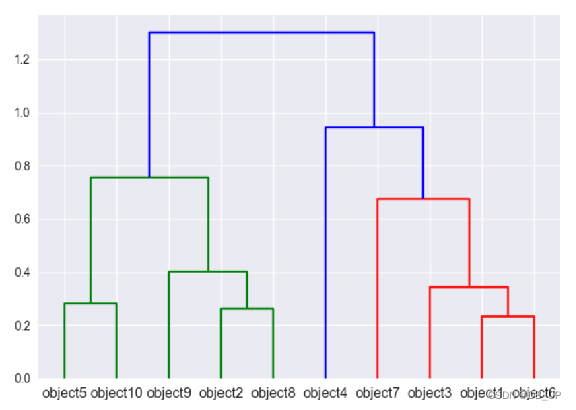
先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后,再计算类与类之间的距离,将距离最近的类合并为一个大类。不停的合并,直到合成了一个类。其中类与类的距离的计算方法有:最短距离法,最长距离法,中间距离法,类平均法等。比如最短距离法,将类与类的距离定义为类与类之间样本的最短距离。
3.1 层次聚类步骤
- 1、首先从 N 个聚类开始,每个数据点一个聚类。
- 2、将彼此靠得最近的两个聚类融合为一个。现在你有 N-1 个聚类。
- 3、重新计算这些聚类之间的距离。
- 4、重复第 2 和 3 步,直到你得到包含 N 个数据点的一个聚类。
- 5、选择一个聚类数量,然后在这个树状图中划一条水平线。
3.2 层次聚类算法优缺点
层次聚类算法优点:
- 1、距离和规则的相似度容易定义,限制少
- 2、不需要预先制定聚类数
- 3、可以发现类的层次关系
- 4、可以聚类成其它形状
层次聚类算法缺点: - 1、计算复杂度太高,不可逆性
- 2、奇异值也能产生很大影响
- 3、算法很可能聚类成链状





 本文详细介绍了三种聚类算法。Kmeans算法通过迭代最小化误差平方和实现收敛,对初始条件敏感;DBSCAN为密度聚类,能发现任意形状聚类且对噪声不敏感;层次聚类则是不断合并距离最近的点或类。文中还阐述了各算法的步骤、优缺点及参数选择等内容。
本文详细介绍了三种聚类算法。Kmeans算法通过迭代最小化误差平方和实现收敛,对初始条件敏感;DBSCAN为密度聚类,能发现任意形状聚类且对噪声不敏感;层次聚类则是不断合并距离最近的点或类。文中还阐述了各算法的步骤、优缺点及参数选择等内容。
















 10万+
10万+










