机器学习算法（一）---决策树

常见的机器学习算法：
机器学习算法（一）—决策树
机器学习算法（二）—支持向量机SVM
机器学习算法（三）—K近邻
机器学习算法（四）—集成算法
基于XGBoost的集成学习算法
基于LightGBM的集成学习算法
机器学习算法（五）—聚类
机器学习算法（六）—逻辑回归
机器学习算法（七）—Apriori 关联分析
机器学习算法（八）—朴素贝叶斯
九种降维方法汇总

一、决策树

1.1、模型介绍

  决策树是一种基本的分类与回归方法，在机器学习中，属于监督学习模型。决策树模型包括：特征选择、决策树生成、决策树剪枝。
  特征选择在于选取对训练数据具有分类能力的特征，这样可以提高决策树的学习效率。决策树在最优特征选取时，常用的算法分为：ID3，C4.5，CART。

1.1.1、ID3算法

  ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归的构建决策树。信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度（定义为一个特征能够为分类系统带来多少信息，带来的信息越多，说明该特征越重要，相应的信息增益也就越大。）
信息增益恰好是：信息熵—条件熵。
熵是表示随机变量不确定性的度量(熵越大，随机变量的不确定性越大)。
信息熵（经验熵）刻画了对数据集进行分类的不确定性。
条件熵（经验条件熵）刻画了在特征A给定条件下，对数据集分类的不确定性。
信息增益刻画了由于特征A的确定，从而使得对数据集的分类的不确定性减少的程度。



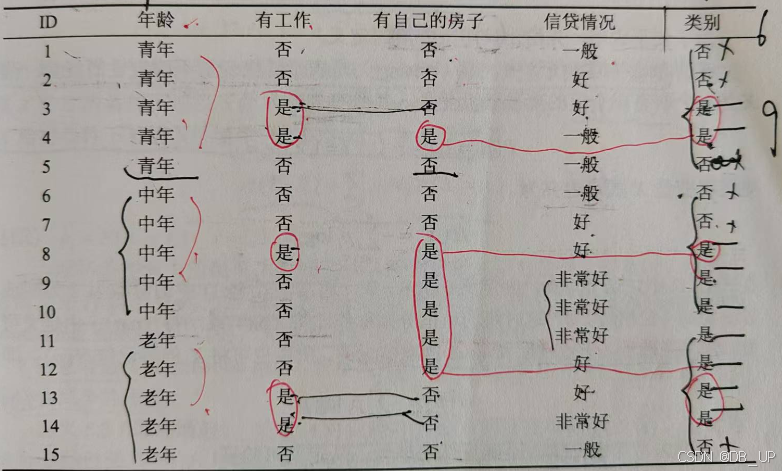
ID3算法的缺点：

• 1.对于缺失值没有考虑
• 2.没有考虑连续特征
• 3.没有考虑过拟合问题，不支持剪枝
• 4.在相同的条件下，取值较多的特征比取值较少的信息增益大

1.1.2、C4.5算法

  C4.5算法与ID3算法相似，C4.5在生成的过程中，用信息增益比来选择特征。



C4.5算法的优、缺点：

为什么说信息增益比比信息增益好？
  因为信息增益会倾向于取值较多的特征，信息增益比本质上是对信息增益乘以一个加权系数，可以在一定程度上对取值较多的特征进行惩罚，避免ID3出现过拟合，提升决策树的泛化能力。

1.1.3、CART算法

  CART算法对于分类树用基尼指数最小化准则进行特征选择，生成二叉树；对于回归树用平方误差最小化准则。

1.1.4、ID3、C4.5、CART树的区别

• ID3只能处理离散型变量；C4.5和CART都可以处理连续型变量。
• ID3对缺失值比较敏感；C4.5和CART都可以处理缺失值。
• ID3和C4.5只能用于分类任务；CART既可以分类，也可以回归
• ID3和C4.5可以在每个节点上产生多分叉分支，且每个特征在层级之间不会复用，CART每个节点只会产生两个分支，因此会形成二叉树，且每个特征可以被重复使用。

1.2、决策树剪枝

重要几个参数

• min_samples_split：节点在分割之前必须具有的最小样本数
• min_samples_leaf：叶子节点必须具有的最小样本数
• max_leaf nodes：叶子节点的最大数量
• max_features：在每个节点处评估用于拆分的最大特征数
• max_depth：树最大的深度
  左图没对参数作限制，模型受异常值影响较大，模型泛化性差；右图设置叶子最小样本数据为4，模型泛化性较好。
  

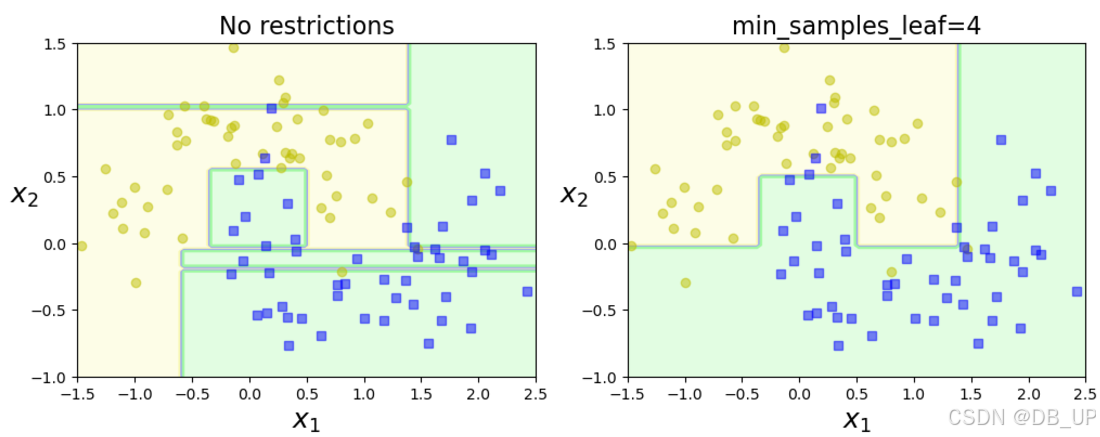
1.3、案例

#使用Titanic数据集，通过特征筛选的方法一步步提升决策树的预测性能
import pandas as pd
from sklearn.model_selection import train_test_split #用于分割数据集
from sklearn.feature_extraction import DictVectorizer #特征转换器
from sklearn.tree import DecisionTreeClassifier  
from sklearn.metrics import classification_report

titanic = pd.read_csv('titanic.csv')
x=titanic[['Pclass','Age','Sex']] 
y=titanic['Survived']

#对缺失数据进行填充
x['Age'].fillna(x['Age'].mean(),inplace=True)

#分割数据，采样25%用于测试
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=33)
#类别特征向量化
vec=DictVectorizer(sparse=False) #会返回一个one-hot编码矩阵
#转换特征后，凡是类别型的特征都单独剥离出来，独成一列特征，数值型的则保持不变
X_train = vec.fit_transform(x_train.to_dict(orient='record'))
X_test=vec.transform(x_test.to_dict(orient='record'))

dtc=DecisionTreeClassifier()#默认criterion='gini'
dtc.fit(X_train,y_train)
dtc_y_predict=dtc.predict(X_test)
print('Accuracy of dtc Classifier:',dtc.score(X_test,y_test))
print(classification_report(y_test,dtc_y_predict))

这里对titanic数据集每列的label进行解释：

• PassengerId：乘客的ID
• Survived：是否存活
• Pclass：船舱等级
• Name：乘客姓名
• Sex：乘客性别
• Age：乘客年龄
• SibSp：有无兄弟姐妹
• Parch：有无父母子女
• Ticket：登船票号
• Fare：票价
• Cabin：船舱类型
• Embarked：所到达的港口

1.4、决策树可视化

安装graphviz

• 根据电脑配置，下载graphviz软件
  graphviz官网

重点：环境变量配置问题

• 下载好文件后，对于用户变量：点击新建->粘贴路径：D:\Graphviz\bin，这边的路径是Graphviz解压的路径
• 对于系统变量：点击新建->粘贴路径：D:\Graphviz\bin\dot.exe，这边的路径是Graphviz解压的路径。
• win+R输入cmd进入windows命令行界面，输入dot -version，如果显示graphviz的相关版本信息，则安装配置成功。

#选择iris数据作为案例
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
from sklearn.tree import export_graphviz
import pydotplus
iris=load_iris()
X=iris.data[:,2:]
y=iris.target
tree_clf=DecisionTreeClassifier(max_depth=3)
tree_clf.fit(X,y)

dot_data=tree.export_graphviz(
    tree_clf,
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True,
    filled=True
)

graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf('iris_tree.pdf')  #生成pdf文件
graph.write_png("iris_tree.png")  #生成png图片

传入参数：

• decision_tree：决策树对象
• out_file：输出文件的句柄或名称。
• max_depth：数的最大深度
• feature_names：特征名称列表
• class_names：类别名称列表，按升序排序
• label：显示纯度信息的选项{‘all’, ‘root’, ‘none’}
• filled：绘制节点以指示分类的多数类、回归值的极值或多输出的节点的纯度。
• leaves_parallel：在树的底部绘制所有叶节点。
• impurity：是否显示纯度显示
• node_ids：是否显示每个节点的ID号
• proportion：将“值”和 “样本量”的显示分别更改为比例。
• rotate：设置未True是从左往右绘制，False是从上往下绘制。
• rounded：设置未True时，使用圆角进行绘制。
• special_characters：设置为时False，忽略特殊字符以实现PostScrip兼容性
• precision：每个节点数值的精度
  

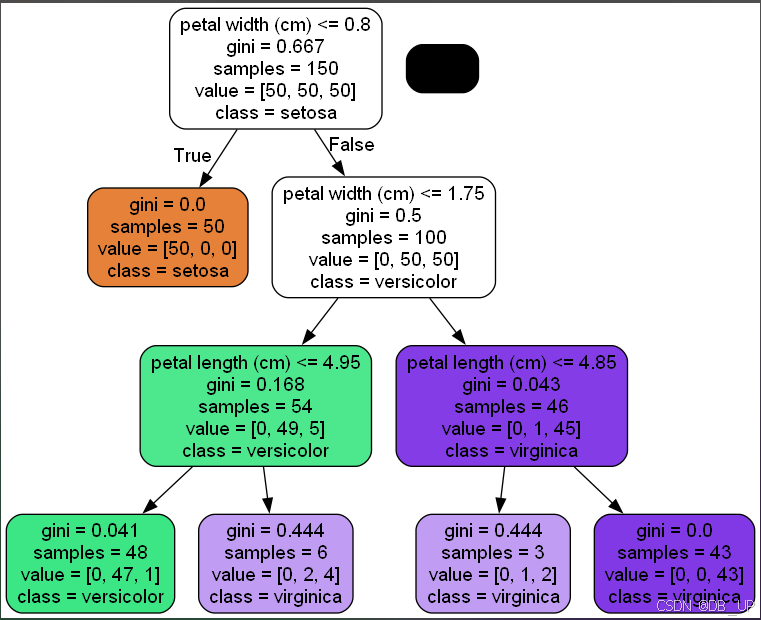
1.5、模型优缺点

决策树的优点：

• 1.简单直观，可解释性强
• 2.基本不需要提前预处理数据
• 3.对于异常值容错能力好，健壮性高
• 4.既可以处理离散值也可以处理连续值(较多算法只专注一种)

决策树的缺点：

• 1.容易过拟合，导致泛化能力不强(限制决策树深度来改进)
• 2.容易因为样本的一点点改动而导致树的结构发生较大改变（可见1.6）
• 3.如：异或，这样的关系决策树难学习

二、决策边界

#决策边界
from sklearn.datasets import load_iris
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np

iris=load_iris()
X=iris.data[:,2:]
y=iris.target
tree_clf=DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X,y)

def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3],iris=True,alpha=0.5,legend=False,plot_training=True):
    x1s = np.linspace(axes[0], axes[1], 100)
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s)
    X_new = np.c_[x1.ravel(), x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custm = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custm)
    if not iris:
        custom = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
        plt.contour(x1, x2, y_pred, cmap=custom, alpha=0.8)
    if plot_training:
        plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", alpha=alpha)
        plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
        plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", alpha=alpha)
    plt.axis(axes)
    if iris:
        plt.xlabel("Petal length", fontsize=14)
        plt.ylabel("Petal width", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    if legend:
        plt.legend(loc="lower right", fontsize=14)

plt.figure(figsize=(10,4))
plot_decision_boundary(tree_clf, X, y)
 
plt.plot([2.45,2.45],[0,3], "k-", alpha=0.5) #添加一条从 (2.45, 0) 到 (2.45, 3) 的黑色垂直实线，
plt.plot([2.45,7.5],[1.75,1.75], "k--", alpha=0.5)
plt.plot([4.95,4.95],[0,1.75], "k:", alpha=0.5)
plt.plot([4.85,4.85],[1.75,3], "k:", alpha=0.5)
plt.text(1.40, 1.0, 'Depth=0', fontsize=14)
plt.text(3.2,1.8, 'Depth=1', fontsize=14)
plt.text(4.05,0.5, 'Depth=2', fontsize=14)
plt.title("Iris classification", fontsize=14)
plt.show()

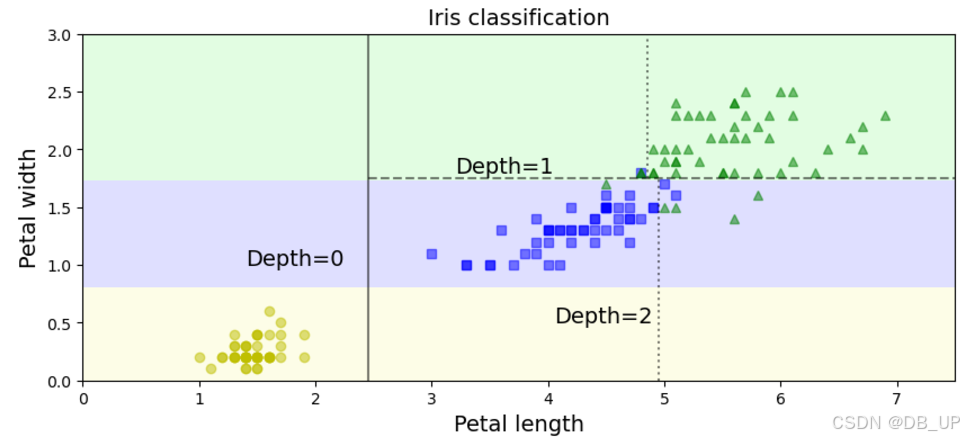
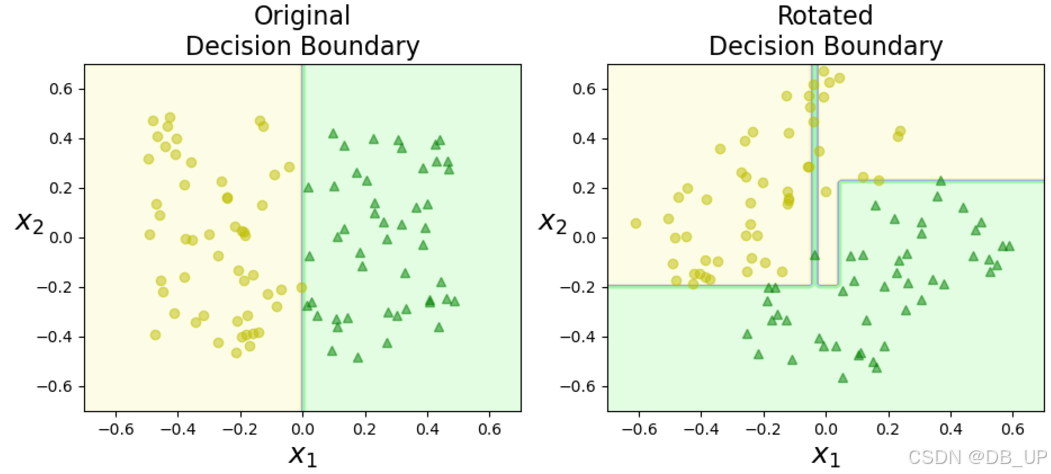
2.1、决策树对数据敏感

将数据旋转45度，决策树模型的结果发生较大改变。

np.random.seed(42)
Xs=np.random.rand(100,2)-0.5
ys=(Xs[:,0]>0).astype(np.float32)*2
angle=np.pi/4
Rot=np.array([[np.cos(angle),-np.sin(angle)],[np.sin(angle),np.cos(angle)]])
Xsr=Xs.dot(Rot)
tree_clf_s=tree.DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs,ys)
tree_clf_sr=tree.DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr,ys)
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s,Xs,ys,axes=[-0.7,0.7,-0.7,0.7],iris=False)
plt.title("Original\nDecision Boundary",fontsize=16)
plt.subplot(122)
plot_decision_boundary(tree_clf_sr,Xsr,ys,axes=[-0.7,0.7,-0.7,0.7],iris=False)
plt.title("Rotated\nDecision Boundary",fontsize=16)
plt.show()