智能优化算法：和声搜索算法-附代码

智能优化算法：和声搜索算法

摘要：和声搜索(Harmony search，HS)算法是 2001 年韩国学者 Geem Z W 等人提出的一种新颖的智能优化算法 [1] 。算法模拟了音乐创作中乐师们凭借自己的记忆,通过反复调整乐队中各乐器的音调, 最终达到一个美
妙的和声状态的过程。该算法简单，寻优能力强。

1.算法原理

HS算法是Geem等人通过类比音乐和最优化问题，的相似性而提出的一种现代启发式智能进化算法。类似于遗传算法对生物进化的模仿、模拟退火算法对物理退火机制的模仿以及粒子群优化算法对鸟群鱼群的模仿等，和声搜索模拟了音乐演奏的原理。音乐和声是一种来源于审美观的，令人欢愉的美妙的声音组合。音乐演奏是要寻找一个由美学评价所决定的最佳状态(极好的和声)，同样最优算法也是寻找由目标函数值所决定的最优状态(全局最优——最低花费、最大利益或效率)。美学评价是由参与演奏的乐器发出的声音集合所决定，正如目标函数值是由设计变量值所组成的集合决定的。

在音乐演奏中，乐师们凭借自己的记忆，通过反复调整乐队中各乐器的音调，最终达到一个美妙的和声状态。Geem Z W 等人受这一现象启发将乐器$i(=1,2,\dots ,m)$类比于优化问题中的第 $i$ 个变量，各乐器的音调相当于各变量的值，各乐器音调的和声相当于优化问题的第 j 组解向量，音乐效果评价类比于目标函数，提出了 HS 算法，图 1 即为即兴音乐创作和工程优化的类比。

图1.音乐创作与优化类比

算法首先初始化和声记忆库，然后从和声记忆库中随机产生新的和声，如果新的和声比记忆库中最差的和声好，把新的和声放进记忆库，把最差的和声换出记忆库。如此循环直至满足停止准则。

和声搜索的计算步骤如下:
Step1: 定义问题与参数值假设问题为最小化，其形式如下:
$$minf(x{)}_{s.t.x_i\in X_i,i=1,2,...,N}\text{\hspace{1em}(1)}$$
这里$f(x)$是目标函数，$x$是由决策变量$x_i$成的解向量$(i=1,2,...,N)$ ，每一个决策的值域为$X_i$。对于离散型变量$X_i=(x_i(1),x_i(2),...,x_i(N))$,而连续型变量:$X_i:x_i^L\le X_i\le x_i^U$, $N$ 为决策变量个数， $K$ 为离散型变量可能值的个数。算法参数有：①和声记忆库的大小 $HMS$ 、②和声记忆库取值概率$HMCR$ 、③音调微调概率 $PAR$ 、④音调微调带宽 $bw$、⑤创作的次数 $Tmax$,各参数在第一步均要被初始化。

Step2: 初始化和声记忆库

随机生成 HMS 个和声放入和声记忆库$(x^1,x^2,...,x^{H}MS)$, 这里和声记忆库可以类比于遗传算法中的种群。

Step3: 生成一个新的和声

生成新的和声$x_j^{{}^{\prime }}=(x_1^{{}^{\prime }},x_2^{{}^{\prime }},...,x_N^{{}^{\prime }})$ ，新和声的每一个音调$x_i^{{}^{\prime }}(i=1,2,...,N)$,通过以下三种机理产生:①学习和声记忆库, ②音调微调, ③随机选择音调。

举例说明：新解的第一个变量 有 $HMCR$ 的概率选自$HM$中$(x_1^{{}^{\prime }}\sim x_1^{HMS})$的任何一个值，有$1-HCMR$的概率选自$HM$外（且在变量范围内）的任何一个值。同样的，其它变量的生成方式如下：
$$x_i^{{}^{\prime }}=\{\begin{array}{l}{x}_i^{{}^{\prime }}\in (x_1^{{}^{\prime }},x_2^{{}^{\prime }},...,x_i^{HMS}),ifrand<HMCR\\ x_i^{{}^{\prime }}\in X_i,otherwise;i=1,2,...,N\end{array}\text{\hspace{1em}(2)}$$
其中 rand 表示[0,1]上的均匀分布的随机数。

其次，如果新的和声$x_j^{{}^{\prime }}$来自和声记忆库 HM，要对其进行音调微调，具体操作如下：
$$x_i^{{}^{\prime }}=\{\begin{array}{l}{x}_i^{{}^{\prime }}+rand1\ast bw,ifrand1<PAR\\ x_i^{{}^{\prime }}\in X_i,otherwise;i=1,2,...,N\end{array}\text{\hspace{1em}(3)}$$
其中，$bw$为音调微调带宽，$PAR$为音调微调概率; $rand1$表示[0,1]上均匀分布的随机数。

Step4: 更新和声记忆库
对 Step3 中的新解进行评估，如果优于 HM 中的函数值最差的一个，则将新解更新至 HM 中。具体操作如下：
$$iff(x^{\prime })<f(x^{worst})then{x}^{worst}=x^{\prime }\text{\hspace{1em}(4)}$$
Step5: 检查是否达到算法终止条件重复步骤 Step3 和 Step4，直到创作(迭代)次数达到 Tmax 为止。

2.实验结果

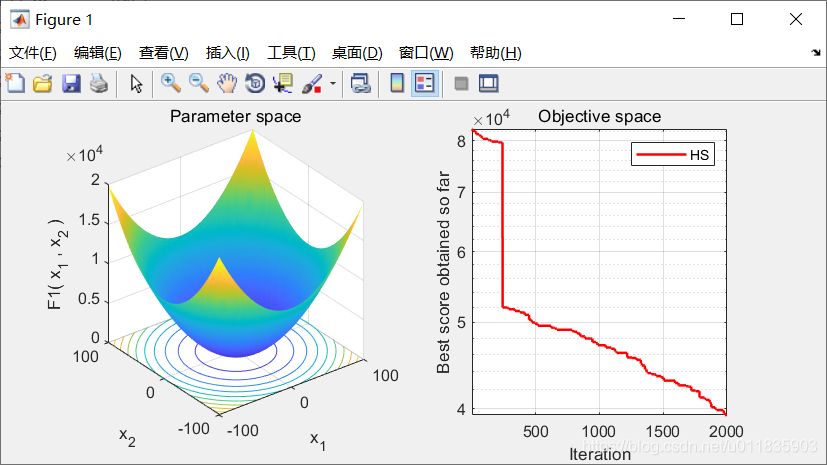
3.参考文献

[1]雍龙泉.和声搜索算法研究进展[J].计算机系统应用,2011,20(07):244-248.

4.Matlab代码

上述代码见个人资料介绍