Codeforces 611C：New Year and Domino 二维前缀和

C. New Year and Domino

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

They say "years are like dominoes, tumbling one after the other". But would a year fit into a grid? I don't think so.

Limak is a little polar bear who loves to play. He has recently got a rectangular grid with h rows and w columns. Each cell is a square, either empty (denoted by '.') or forbidden (denoted by '#'). Rows are numbered 1 through h from top to bottom. Columns are numbered1 through w from left to right.

Also, Limak has a single domino. He wants to put it somewhere in a grid. A domino will occupy exactly two adjacent cells, located either in one row or in one column. Both adjacent cells must be empty and must be inside a grid.

Limak needs more fun and thus he is going to consider some queries. In each query he chooses some rectangle and wonders, how many way are there to put a single domino inside of the chosen rectangle?

Input

The first line of the input contains two integers h and w (1 ≤ h, w ≤ 500) – the number of rows and the number of columns, respectively.

The next h lines describe a grid. Each line contains a string of the length w. Each character is either '.' or '#' — denoting an empty or forbidden cell, respectively.

The next line contains a single integer q (1 ≤ q ≤ 100 000) — the number of queries.

Each of the next q lines contains four integers r1i, c1i, r2i, c2i (1 ≤ r1i ≤ r2i ≤ h, 1 ≤ c1i ≤ c2i ≤ w) — the i-th query. Numbers r1i andc1i denote the row and the column (respectively) of the upper left cell of the rectangle. Numbers r2i and c2i denote the row and the column (respectively) of the bottom right cell of the rectangle.

Output

Print q integers, i-th should be equal to the number of ways to put a single domino inside the i-th rectangle.

Sample test(s)

input

5 8
....#..#
.#......
##.#....
##..#.##
........
4
1 1 2 3
4 1 4 1
1 2 4 5
2 5 5 8

output

4
0
10
15

input

7 39
.......................................
.###..###..#..###.....###..###..#..###.
...#..#.#..#..#.........#..#.#..#..#...
.###..#.#..#..###.....###..#.#..#..###.
.#....#.#..#....#.....#....#.#..#..#.#.
.###..###..#..###.....###..###..#..###.
.......................................
6
1 1 3 20
2 10 6 30
2 10 7 30
2 2 7 7
1 7 7 7
1 8 7 8

output

53
89
120
23
0
2

Note

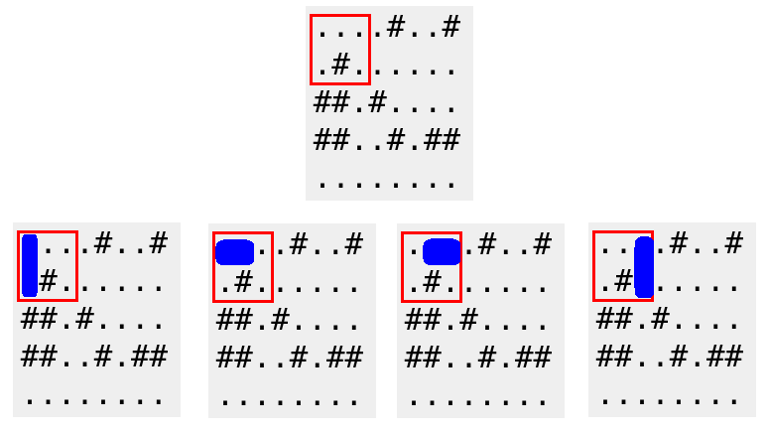
A red frame below corresponds to the first query of the first sample. A domino can be placed in 4 possible ways.

把题目想复杂了，每次都不看输入数据规模，实际上这个题目复杂度O(q*(m+n))轻松过。。。

题意是每次给出一块矩形区域，往里面放一个1*2的多米诺骨牌，里面有"#"不能放。问每次的矩形有多少种放多米诺骨牌的方法。

递推+二维的前缀和。

每次查询就先算每一行有多少种，前缀和相减。之后算每一列有多少种，也是前缀和相减。

代码：

#pragma warning(disable:4996)  
#include <iostream>  
#include <algorithm>
#include <cstring>
#include <cstring>
#include <vector>  
#include <string>  
#include <cmath>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;

#define INF 0x3fffffffffffffff
const int maxn = 505;

int h, w, q;
char val[maxn][maxn];
int prerow[maxn][maxn];
int precol[maxn][maxn];

void input()
{
	int i, j;
	scanf("%d%d", &h, &w);

	for (i = 1; i <= h; i++)
	{
		scanf("%s", val[i] + 1);
		for (j = 1; j <= w; j++)
		{
			if (val[i][j] == '.'&&val[i][j - 1] == '.')
			{
				prerow[i][j] = 1 + prerow[i][j - 1];
			}
			else
			{
				prerow[i][j] = prerow[i][j - 1];
			}
		}
	}
	for (j = 1; j <= w; j++)
	{
		for (i = 1; i <= h; i++)
		{
			if (val[i][j] == '.'&&val[i - 1][j] == '.')
			{
				precol[i][j] = precol[i - 1][j] + 1;
			}
			else
			{
				precol[i][j] = precol[i - 1][j];
			}
		}
	}
}

void solve()
{
	int i, j;
	int r1, c1, r2, c2;
	
	scanf("%d", &q);
	
	ll res = 0;
	for (i = 1; i <= q; i++)
	{
		scanf("%d%d%d%d", &r1, &c1, &r2, &c2);
		
		res = 0;
		for (j = r1 ; j <= r2; j++)
		{
			res += (prerow[j][c2] - prerow[j][c1]);
		}
		for (j = c1; j <= c2; j++)
		{
			res += (precol[r2][j] - precol[r1][j]);
		}

		printf("%I64d\n", res);
	}
}

int main()
{
	//freopen("i.txt", "r", stdin);
	//freopen("o.txt", "w", stdout);

	input();
	solve();
	
	//system("pause");
	return 0;
}